Файл: 1. Жиындар жне олара амалдар олдану. Мысал келтірііз. Эйлер Венн диаграммасы бойынша крсетііз.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
С оқиғасын айтамыз. Бұл 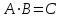 деп белгіленеді.
деп белгіленеді.  оқиғаларының көбейтіндісі деп, олардың бәрінің бірге пайда болуынан тұратын С оқиғасын айтамыз. Яғни,
оқиғаларының көбейтіндісі деп, олардың бәрінің бірге пайда болуынан тұратын С оқиғасын айтамыз. Яғни, 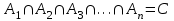 .
.
Мысалы, нысанаға үш мерген, бір- біріне тәуілсіз, оқ атады делік. Егер - оқиғасы- бірінші мергенның оғының нысанаға даруы,
- оқиғасы- бірінші мергенның оғының нысанаға даруы,  - екіншісінікі,
- екіншісінікі,  - үшіншісінікі десек, онда
- үшіншісінікі десек, онда 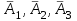 ,
,  оқиғаларына қарама- қарсы оқиғалар
оқиғаларына қарама- қарсы оқиғалар
4. Қарапайым (элементарлы) оқиғалар кеңістігінің оқиғалары. Оқиғалар алгебрасы. Анықтамасы, түрлері, қасиеттері. Мысал келтіріңіз.
5. Ықтималдықтың классикалық анықтамасы. Оқиға ықтималдығының қасиеттері. түрлері. Мысал келтіріңіз.
Жоғарыда біз оқиға түрлеріне мысалдар келтірдік, енді оқиғаның пайда болуы мүмкіндігінің сандық өлшеуішін көрсетеміз. Жалпы айтқанда, А оқиғасының пайда болу мүмкіндігінің сандық мөлшеріне р(А) функциясының мәні алынады. Мұны осы А оқиғасының ықтималдығы деп атайды.
Қандай болмасын математикалық теория белгілі бір ұғымдар негізінде құралатын болғандықтан, біз ықтималдықтар теориясының құрылуын ықтималдықтың классикалық анықтамасына негіздейміз.
Ықтималдықтың классикалық анықтамасын алғаш рет берген Лаплас еді.
Ықтималдықтың классикалық анықтамасы оқиғалардың тең мүмкіндіктеріне (тең ықтималдығына) сүйенеді.
Тең мүмкіндік немесе тең ықтималдық ұғымдары алғашқы ұғымдарға жатады, олар логикалық (формальді) анықтама беруді қажет етпейді. Жалпы сынау нәтижесінде бірнеше оқиғалар пайда болуы мүмкін болса және олардың біреуінің пайда болуы мүмкіндігінің, екіншісіне қарағанда, артықшылығы бар деп айта алмайтын болсақ, яғни сынаулар нәтижесінің симметриялы қасиеті болса, мұндай оқиғалар тең мүмкіндікті делінеді.
Бірнеше оқиғалар тең мүмкіндікті, қос-қостан үйлесімсіз және оқиғалардың толық тобын құраса, онда ол оқиғаларды сынаудың мүмкін нәтижелерінің толық тобы деп атайды. Бұл терминнің орнына тең мүмкіндікті барлық жағдайлар немесе жалпы жағдайлар саны не, қысқаша жағдайлар деп атайды.
Ал тең мүмкіндікті үйлесімсіз және оқиғалардың толық тобын құрайтын оқиғалардың (жағдайлардың) бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін. Бұл оқиғаларды қолайлы жағдайлар деп атайды.
Анықтама. А оқиғасы қолайлы жағдайлар санының (т) сынаудың тең мүмкіндікті барлық жағдайлар санын (п) қатынасын А оқиғасының ықтималдығы деп атайды және былай жазады:
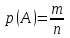 (1)
(1)
Ықтималдықтың бұл анықтамасын классикалық анықтама дейміз. Бұдан төмендегі салдар шығады.
Шынында, оқиға ақиқат болу үшін А оқиғасына қолайлы жағдайлар саны т сынаудың барлық тең мүмкіндікті жағдайлар саны п-ге тең, яғни m=n болады. Онда (1) бойынша
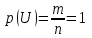 (2)
(2)
Шынында да, егер оқиға мүмкін емес болса, онда А оқиғасына қолайлы жағдайлар саны т нөльге тең болады. Олай болса
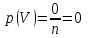 (3)
(3)
3. А оқиғасының ықтималдығы р(А) нөль мен бір аралығындағы оң таңбалы сан. Шынында, А оқиғасына қолайлы жағдайлар саны т нөльден п-ге дейінгі, өздерін қоса алғандағы, мәндерді қабылдайды, яғни
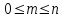 ,
,
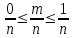 немесе
немесе 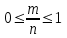
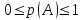 (4)
(4)
Оқиғаның ықтималдығы дегеніміз – осы оқиғаға қолайлы жағдайлар санының барлық жағдайлар санына қатынасы.
Егер де тең және жалғыз мүмкінді сыйыспайтын барлық n – жағдайлардың ішінде m саны осы А – оқиғасының орындалуына қолайлы жағдайлар саны болса, онда m санының барлық n – санына қатынасын осы А оқиғасының орындалуының ықтималдығы дейміз, оны Р(А) деп белгілейміз:
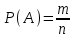 бұл француз ғалымы Лаплас берген (1749 – 1827жж.) анықтама.
бұл француз ғалымы Лаплас берген (1749 – 1827жж.) анықтама.
1 – мысал. Екі теңгені лақтырғанда ең болмағанда бір рет «сан» жағының түсу ықтималдығы қандай?
Шешуі: Тәжірибе – 2 теңгені лақтыру. Сонда элементер оқиғалар кеңістігі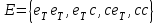 болады. Олай болса n = 4. А оқиғасы ең болмағанда бір рет «с»жағының түсуі. Демек m = 3. Сондықтан,
болады. Олай болса n = 4. А оқиғасы ең болмағанда бір рет «с»жағының түсуі. Демек m = 3. Сондықтан,
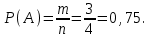
2 – мысал. Ойын сүйегін екі рет лақтырғанда пайда болғн ұпайлардың қосындысы 6 – ға тең болу ықтималдығы қандай?
Шешуі: Тәжірибе, ойын сүйегін екі рет лақтыру болады. Сонда
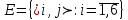 , яғни
, яғни 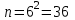 .
.
А оқиғасы – ұпайлардың қосындысы алтыға тең болуы:
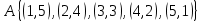 ,
, 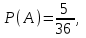 өйткені элементар оқиғалар саны 36 – ға тең, ал А – ға қолайлы жағдайлар саны 5 – ке тең.
өйткені элементар оқиғалар саны 36 – ға тең, ал А – ға қолайлы жағдайлар саны 5 – ке тең.
3– мысал.Тиынды 1 рет лақтырайық. «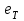 » пайда болу ықтималдығын табу керек.
» пайда болу ықтималдығын табу керек.
Шешуі: тиынды лақтырғандағы «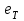 » пайда болу ықтималдығы
» пайда болу ықтималдығы
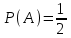 .
.
Ықтималдықтың негізгі қасиеттері
Ақиқат оқиғаның ықтималдығы бірге тең, яғни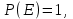 шыныңда, ақиқат оқиғаға барлық элементер оқиғалар қолайлы болады. Сондықтан
шыныңда, ақиқат оқиғаға барлық элементер оқиғалар қолайлы болады. Сондықтан 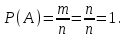
Мүмкін емес оқиғаның ықтималдығы нөлге тең, яғни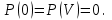 Шынында мүмкін емес оқиғаға ешбір элементар оқиғи қолайлы емес. Демек
Шынында мүмкін емес оқиғаға ешбір элементар оқиғи қолайлы емес. Демек 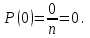
кездейсоқ оқиғаның ықтималдығы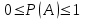 теңсіздігін қанағаттандырады.
теңсіздігін қанағаттандырады.
Шынында, А оқиғасына «қолайлы» жағдайлар саны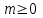 және барлық жағдайлар саны үшін
және барлық жағдайлар саны үшін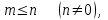 демек
демек 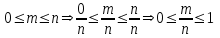 .
.
4 – мысал. 36 картаның ішінен тәуекелге үш картаны суырып алайық. Осы 3 картаны 2-інің «тұз» болуының ықтималдығын табу керек.
Шешуі: «А» біздің іздеп отырған оқиғамыз болсын. Жалпы жағдайлар саны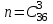 . Ал, «А» оқиғасына «қолайлы жағдайлар» саны - m, ол
. Ал, «А» оқиғасына «қолайлы жағдайлар» саны - m, ол 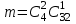 .
.
Сондықтан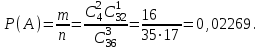
5- мысал. Жәшікте барлығы N шарлар бар, оның ішінде n қара шар бар, ал (N - n) – көк шарлар. Жәшіктен кез келген m шар алынды. Сол алынған m шардың ішінде k қара шар болуының ықтималдығы қандай?
Шешуі: Жәшіктегі N шардан m шарды әр түрлі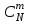 жолмен алуға болады. Ал, n қара шардан k шарды әр түрлі
жолмен алуға болады. Ал, n қара шардан k шарды әр түрлі 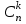 жолмен алуға болады.Сонда алынған m шардың ішінде m – k көк шарлар болғандықтан барлық N - n көк шарлардан m – k көк шарды
жолмен алуға болады.Сонда алынған m шардың ішінде m – k көк шарлар болғандықтан барлық N - n көк шарлардан m – k көк шарды 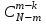 жолмен алуға болды екен. Олай болса, комбинаторикадағы көбейту ережесін қолдансақ, алынған m шардың ішінде k - қара шар, m – k - көк шар болуы
жолмен алуға болды екен. Олай болса, комбинаторикадағы көбейту ережесін қолдансақ, алынған m шардың ішінде k - қара шар, m – k - көк шар болуы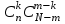 жолмен анықталады.
жолмен анықталады.
Сонда ықтималдықтың классикалық анықтамасы бойынша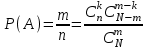 .
.
6. Салыстырмалы жиілік. Статистикалық ықтималдық. Геометриялық ықтималдық. Анықтамасы, мысал келтіріңіз.
Салыстырмалы жиілікте анықтама беру үшін мынадай мысал қарастыралық. n рет тәжірибе қайталанып жүргізілді делік, әр тәжірибеде А оқиғасының пайда болған, болмағанын есептеп отыралық. Сонда n тәжірибеде А оқиғасы m реет пайда болсын. А оқиғасының пайда болу санының тәжірибенің қайталану санына қатынасын,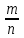 бөлшегін, А оқиғасының пайда болу жиілігі деп атайды.
бөлшегін, А оқиғасының пайда болу жиілігі деп атайды.
Тәжірибенің қайталану саны мейлінше үлкен болғанда жиілік тұрақты бір санның төңірегінде (маңайында) тығыз топталады екен. Осы заңдылықты СТАТИСТИКАЛЫҚ Т¦РАҚТЫЛЫҚ деп атайды.
Мысалға, XVIII ғасырда француз ғалымы Бюффон, үлкен сандар заңын тіжірибе арқылы тексеру кезінде, теңгені 4040 рет лақтырғанда «герб» 2048 рет пайда болған, сонда «герб» түсу жиілігі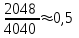 -тің маңайына болатынын анықталған. Сонымен, салыстырмалы жиілік W(A) деп, жасалынған тәжірибеде А оқиғасының пайда болған санының (m) барлық қайталанған тәжірибе санына (n) қатынасын айтады.
-тің маңайына болатынын анықталған. Сонымен, салыстырмалы жиілік W(A) деп, жасалынған тәжірибеде А оқиғасының пайда болған санының (m) барлық қайталанған тәжірибе санына (n) қатынасын айтады.
W(A)=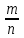
Мысалдар. 1. 100 рет оқ атылғанда, нысанаға 76 рет тигені (А) байқалды. Нысанаға оқтың тию «жиілігі» қандай ?
Шешуі. Мұндағы m=76, n=100, ендеше
W(A)=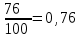
2.Техникалық бақылау бөліміне түскен 100 пар аяқ киімнің төртеуі жарамсыз болып шықты. Жарамсыз аяқ киімдердің салыстырмалы жиілігі қандай?
Шешуі.n=100, m=4, онда
W(A)=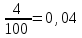
Ықтималдықтың классикалық және статистикалық анықтамаларын салыстыра отырып, мынадай қортындыға келуге болады: ықтималдықтың классикалық анықтамасы тәрибенің шындығында болуын талап етпейді, ал салыстырмалы жиіліктің анықтымасы (статистикалық анықтама) тәжірибеде жасалынған деп ұйғарып есептелінеді. Басқаша айтқанда, ықтималдық тәжірибеге дейін, ал жиілік тәжірибеден кейін есептелінеді.
7. Комбинаторика ұғымы. Қайталанбайтын комбинаториканың формулалары: орналастыру, алмастыру, теру. Терудің қасиеттері. Анықтамасы. Мысал келтіріңіз.
8. Қайталанбалы комбинаториканың формулалары: орналастыру, алмастыру, теру. Анықтамасы. Қасиеттері. Мысал келтіріңіз.
9. Ықтималдықтарды қосу теоремалары. Салдарлары. Мысал келтіріңіз.
10. Ықтималдықтарды көбейту теоремалары. Шартты ықтималдық. Анықтамасы. Мысал келтіріңіз.
Ықтималдықтарды көбейту
Егер А оқиғасының ықтималдығы В оқиғасының пайда болғанына, немесе пайда болмағанына тәуелсіз болса, онда А оқиғасы В оқиғасына тәуелсіз деп аталады.
Егер А оқиғасының ықтималдығы В оқиғасының пайда болғанына, немесе болмағанына байланысты өзгеретін болса, онда А оқиғасы В оқиғасының тәуелді деп аталады.
1 мысал. Екі атқыш нысанаға оқ атуда. Бірінші атқыштың нысанаға тигізу ықтималдығы Р(А) екінші атқыштың оқ тигізуіне, немесе мүлт кетуіне тәуелді емес. Екінші атқыштың оқ тигізу ықтималдығы да бірінші атқыштың нәтижесінде тәуелді емес. А және В тәуелсіз оқиғалар.
2 мысал. Жәшікте 3 ақ және 2 қара шар бар. Қалай болса солай жәшіктен бір шар алынған. Ақ шар алу ықтималдығы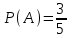 . Шарды қайтадан жәшікке салып, тәжірибені қайталайды. Екінші тәжірибеде де жәшіктен ақ шар алу ықөтималдығы
. Шарды қайтадан жәшікке салып, тәжірибені қайталайды. Екінші тәжірибеде де жәшіктен ақ шар алу ықөтималдығы 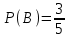 -ке тең және ол бірінші тәжірибенің нәтижесінде тәуелді емес. Бұл жағдайда да А және В тәуелсіз оқиғалар.
-ке тең және ол бірінші тәжірибенің нәтижесінде тәуелді емес. Бұл жағдайда да А және В тәуелсіз оқиғалар.
3 мысал.Жәшікте 3 ақ, 2 қара шар бар. Жәшіктен бірінен соң бірі екі шар алынған. Бірінші тәжірибеде ақ шар алу ықтималдығы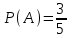 . Екінші рет ақ шар алу ықтималдығы
. Екінші рет ақ шар алу ықтималдығы 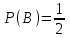 бірінші тәжірибенің ықтималдығына тәуелді. Бұл мысалда А мен В тәуелді оқиғалар. Егер бірнеше оқиғалардың әрбір екеуі өзара тәуелсіз болса, онда оларды қос-қостан тәуелсіз оқиғалар деп атайды.
бірінші тәжірибенің ықтималдығына тәуелді. Бұл мысалда А мен В тәуелді оқиғалар. Егер бірнеше оқиғалардың әрбір екеуі өзара тәуелсіз болса, онда оларды қос-қостан тәуелсіз оқиғалар деп атайды.
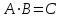 деп белгіленеді.
деп белгіленеді.  оқиғаларының көбейтіндісі деп, олардың бәрінің бірге пайда болуынан тұратын С оқиғасын айтамыз. Яғни,
оқиғаларының көбейтіндісі деп, олардың бәрінің бірге пайда болуынан тұратын С оқиғасын айтамыз. Яғни, 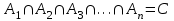 .
. Мысалы, нысанаға үш мерген, бір- біріне тәуілсіз, оқ атады делік. Егер
 - оқиғасы- бірінші мергенның оғының нысанаға даруы,
- оқиғасы- бірінші мергенның оғының нысанаға даруы,  - екіншісінікі,
- екіншісінікі,  - үшіншісінікі десек, онда
- үшіншісінікі десек, онда 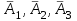 ,
,  оқиғаларына қарама- қарсы оқиғалар
оқиғаларына қарама- қарсы оқиғалар4. Қарапайым (элементарлы) оқиғалар кеңістігінің оқиғалары. Оқиғалар алгебрасы. Анықтамасы, түрлері, қасиеттері. Мысал келтіріңіз.
5. Ықтималдықтың классикалық анықтамасы. Оқиға ықтималдығының қасиеттері. түрлері. Мысал келтіріңіз.
Жоғарыда біз оқиға түрлеріне мысалдар келтірдік, енді оқиғаның пайда болуы мүмкіндігінің сандық өлшеуішін көрсетеміз. Жалпы айтқанда, А оқиғасының пайда болу мүмкіндігінің сандық мөлшеріне р(А) функциясының мәні алынады. Мұны осы А оқиғасының ықтималдығы деп атайды.
Қандай болмасын математикалық теория белгілі бір ұғымдар негізінде құралатын болғандықтан, біз ықтималдықтар теориясының құрылуын ықтималдықтың классикалық анықтамасына негіздейміз.
Ықтималдықтың классикалық анықтамасын алғаш рет берген Лаплас еді.
Ықтималдықтың классикалық анықтамасы оқиғалардың тең мүмкіндіктеріне (тең ықтималдығына) сүйенеді.
Тең мүмкіндік немесе тең ықтималдық ұғымдары алғашқы ұғымдарға жатады, олар логикалық (формальді) анықтама беруді қажет етпейді. Жалпы сынау нәтижесінде бірнеше оқиғалар пайда болуы мүмкін болса және олардың біреуінің пайда болуы мүмкіндігінің, екіншісіне қарағанда, артықшылығы бар деп айта алмайтын болсақ, яғни сынаулар нәтижесінің симметриялы қасиеті болса, мұндай оқиғалар тең мүмкіндікті делінеді.
Бірнеше оқиғалар тең мүмкіндікті, қос-қостан үйлесімсіз және оқиғалардың толық тобын құраса, онда ол оқиғаларды сынаудың мүмкін нәтижелерінің толық тобы деп атайды. Бұл терминнің орнына тең мүмкіндікті барлық жағдайлар немесе жалпы жағдайлар саны не, қысқаша жағдайлар деп атайды.
Ал тең мүмкіндікті үйлесімсіз және оқиғалардың толық тобын құрайтын оқиғалардың (жағдайлардың) бірнешеуі бір А оқиғасының пайда болуын тудыруы мүмкін. Бұл оқиғаларды қолайлы жағдайлар деп атайды.
Анықтама. А оқиғасы қолайлы жағдайлар санының (т) сынаудың тең мүмкіндікті барлық жағдайлар санын (п) қатынасын А оқиғасының ықтималдығы деп атайды және былай жазады:
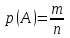 (1)
(1)Ықтималдықтың бұл анықтамасын классикалық анықтама дейміз. Бұдан төмендегі салдар шығады.
-
Ақиқат оқиға ықтималдығы 1-ге тең.
Шынында, оқиға ақиқат болу үшін А оқиғасына қолайлы жағдайлар саны т сынаудың барлық тең мүмкіндікті жағдайлар саны п-ге тең, яғни m=n болады. Онда (1) бойынша
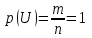 (2)
(2)-
Мүмкін емес оқиға ықтималдығы нөлге тең.
Шынында да, егер оқиға мүмкін емес болса, онда А оқиғасына қолайлы жағдайлар саны т нөльге тең болады. Олай болса
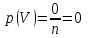 (3)
(3)3. А оқиғасының ықтималдығы р(А) нөль мен бір аралығындағы оң таңбалы сан. Шынында, А оқиғасына қолайлы жағдайлар саны т нөльден п-ге дейінгі, өздерін қоса алғандағы, мәндерді қабылдайды, яғни
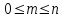 ,
,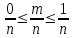 немесе
немесе 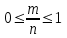
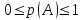 (4)
(4)Оқиғаның ықтималдығы дегеніміз – осы оқиғаға қолайлы жағдайлар санының барлық жағдайлар санына қатынасы.
Егер де тең және жалғыз мүмкінді сыйыспайтын барлық n – жағдайлардың ішінде m саны осы А – оқиғасының орындалуына қолайлы жағдайлар саны болса, онда m санының барлық n – санына қатынасын осы А оқиғасының орындалуының ықтималдығы дейміз, оны Р(А) деп белгілейміз:
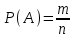 бұл француз ғалымы Лаплас берген (1749 – 1827жж.) анықтама.
бұл француз ғалымы Лаплас берген (1749 – 1827жж.) анықтама.1 – мысал. Екі теңгені лақтырғанда ең болмағанда бір рет «сан» жағының түсу ықтималдығы қандай?
Шешуі: Тәжірибе – 2 теңгені лақтыру. Сонда элементер оқиғалар кеңістігі
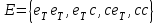 болады. Олай болса n = 4. А оқиғасы ең болмағанда бір рет «с»жағының түсуі. Демек m = 3. Сондықтан,
болады. Олай болса n = 4. А оқиғасы ең болмағанда бір рет «с»жағының түсуі. Демек m = 3. Сондықтан,
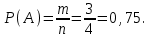
2 – мысал. Ойын сүйегін екі рет лақтырғанда пайда болғн ұпайлардың қосындысы 6 – ға тең болу ықтималдығы қандай?
Шешуі: Тәжірибе, ойын сүйегін екі рет лақтыру болады. Сонда
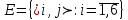 , яғни
, яғни 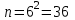 .
.А оқиғасы – ұпайлардың қосындысы алтыға тең болуы:
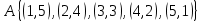 ,
, 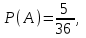 өйткені элементар оқиғалар саны 36 – ға тең, ал А – ға қолайлы жағдайлар саны 5 – ке тең.
өйткені элементар оқиғалар саны 36 – ға тең, ал А – ға қолайлы жағдайлар саны 5 – ке тең.3– мысал.Тиынды 1 рет лақтырайық. «
 » пайда болу ықтималдығын табу керек.
» пайда болу ықтималдығын табу керек.Шешуі: тиынды лақтырғандағы «
 » пайда болу ықтималдығы
» пайда болу ықтималдығы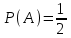 .
.Ықтималдықтың негізгі қасиеттері
Ақиқат оқиғаның ықтималдығы бірге тең, яғни
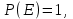 шыныңда, ақиқат оқиғаға барлық элементер оқиғалар қолайлы болады. Сондықтан
шыныңда, ақиқат оқиғаға барлық элементер оқиғалар қолайлы болады. Сондықтан 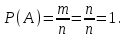
Мүмкін емес оқиғаның ықтималдығы нөлге тең, яғни
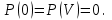 Шынында мүмкін емес оқиғаға ешбір элементар оқиғи қолайлы емес. Демек
Шынында мүмкін емес оқиғаға ешбір элементар оқиғи қолайлы емес. Демек 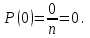
кездейсоқ оқиғаның ықтималдығы
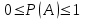 теңсіздігін қанағаттандырады.
теңсіздігін қанағаттандырады.Шынында, А оқиғасына «қолайлы» жағдайлар саны
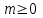 және барлық жағдайлар саны үшін
және барлық жағдайлар саны үшін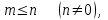 демек
демек 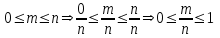 .
.4 – мысал. 36 картаның ішінен тәуекелге үш картаны суырып алайық. Осы 3 картаны 2-інің «тұз» болуының ықтималдығын табу керек.
Шешуі: «А» біздің іздеп отырған оқиғамыз болсын. Жалпы жағдайлар саны
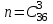 . Ал, «А» оқиғасына «қолайлы жағдайлар» саны - m, ол
. Ал, «А» оқиғасына «қолайлы жағдайлар» саны - m, ол 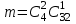 .
.Сондықтан
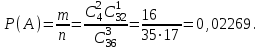
5- мысал. Жәшікте барлығы N шарлар бар, оның ішінде n қара шар бар, ал (N - n) – көк шарлар. Жәшіктен кез келген m шар алынды. Сол алынған m шардың ішінде k қара шар болуының ықтималдығы қандай?
Шешуі: Жәшіктегі N шардан m шарды әр түрлі
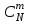 жолмен алуға болады. Ал, n қара шардан k шарды әр түрлі
жолмен алуға болады. Ал, n қара шардан k шарды әр түрлі 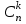 жолмен алуға болады.Сонда алынған m шардың ішінде m – k көк шарлар болғандықтан барлық N - n көк шарлардан m – k көк шарды
жолмен алуға болады.Сонда алынған m шардың ішінде m – k көк шарлар болғандықтан барлық N - n көк шарлардан m – k көк шарды 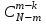 жолмен алуға болды екен. Олай болса, комбинаторикадағы көбейту ережесін қолдансақ, алынған m шардың ішінде k - қара шар, m – k - көк шар болуы
жолмен алуға болды екен. Олай болса, комбинаторикадағы көбейту ережесін қолдансақ, алынған m шардың ішінде k - қара шар, m – k - көк шар болуы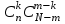 жолмен анықталады.
жолмен анықталады.Сонда ықтималдықтың классикалық анықтамасы бойынша
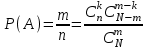 .
.6. Салыстырмалы жиілік. Статистикалық ықтималдық. Геометриялық ықтималдық. Анықтамасы, мысал келтіріңіз.
Салыстырмалы жиілікте анықтама беру үшін мынадай мысал қарастыралық. n рет тәжірибе қайталанып жүргізілді делік, әр тәжірибеде А оқиғасының пайда болған, болмағанын есептеп отыралық. Сонда n тәжірибеде А оқиғасы m реет пайда болсын. А оқиғасының пайда болу санының тәжірибенің қайталану санына қатынасын,
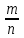 бөлшегін, А оқиғасының пайда болу жиілігі деп атайды.
бөлшегін, А оқиғасының пайда болу жиілігі деп атайды.Тәжірибенің қайталану саны мейлінше үлкен болғанда жиілік тұрақты бір санның төңірегінде (маңайында) тығыз топталады екен. Осы заңдылықты СТАТИСТИКАЛЫҚ Т¦РАҚТЫЛЫҚ деп атайды.
Мысалға, XVIII ғасырда француз ғалымы Бюффон, үлкен сандар заңын тіжірибе арқылы тексеру кезінде, теңгені 4040 рет лақтырғанда «герб» 2048 рет пайда болған, сонда «герб» түсу жиілігі
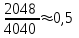 -тің маңайына болатынын анықталған. Сонымен, салыстырмалы жиілік W(A) деп, жасалынған тәжірибеде А оқиғасының пайда болған санының (m) барлық қайталанған тәжірибе санына (n) қатынасын айтады.
-тің маңайына болатынын анықталған. Сонымен, салыстырмалы жиілік W(A) деп, жасалынған тәжірибеде А оқиғасының пайда болған санының (m) барлық қайталанған тәжірибе санына (n) қатынасын айтады.W(A)=
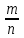
Мысалдар. 1. 100 рет оқ атылғанда, нысанаға 76 рет тигені (А) байқалды. Нысанаға оқтың тию «жиілігі» қандай ?
Шешуі. Мұндағы m=76, n=100, ендеше
W(A)=
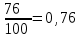
2.Техникалық бақылау бөліміне түскен 100 пар аяқ киімнің төртеуі жарамсыз болып шықты. Жарамсыз аяқ киімдердің салыстырмалы жиілігі қандай?
Шешуі.n=100, m=4, онда
W(A)=
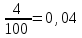
Ықтималдықтың классикалық және статистикалық анықтамаларын салыстыра отырып, мынадай қортындыға келуге болады: ықтималдықтың классикалық анықтамасы тәрибенің шындығында болуын талап етпейді, ал салыстырмалы жиіліктің анықтымасы (статистикалық анықтама) тәжірибеде жасалынған деп ұйғарып есептелінеді. Басқаша айтқанда, ықтималдық тәжірибеге дейін, ал жиілік тәжірибеден кейін есептелінеді.
7. Комбинаторика ұғымы. Қайталанбайтын комбинаториканың формулалары: орналастыру, алмастыру, теру. Терудің қасиеттері. Анықтамасы. Мысал келтіріңіз.
8. Қайталанбалы комбинаториканың формулалары: орналастыру, алмастыру, теру. Анықтамасы. Қасиеттері. Мысал келтіріңіз.
9. Ықтималдықтарды қосу теоремалары. Салдарлары. Мысал келтіріңіз.
10. Ықтималдықтарды көбейту теоремалары. Шартты ықтималдық. Анықтамасы. Мысал келтіріңіз.
Ықтималдықтарды көбейту
-
Тәуелсіз және тәуелді оқиғалар
Егер А оқиғасының ықтималдығы В оқиғасының пайда болғанына, немесе пайда болмағанына тәуелсіз болса, онда А оқиғасы В оқиғасына тәуелсіз деп аталады.
Егер А оқиғасының ықтималдығы В оқиғасының пайда болғанына, немесе болмағанына байланысты өзгеретін болса, онда А оқиғасы В оқиғасының тәуелді деп аталады.
1 мысал. Екі атқыш нысанаға оқ атуда. Бірінші атқыштың нысанаға тигізу ықтималдығы Р(А) екінші атқыштың оқ тигізуіне, немесе мүлт кетуіне тәуелді емес. Екінші атқыштың оқ тигізу ықтималдығы да бірінші атқыштың нәтижесінде тәуелді емес. А және В тәуелсіз оқиғалар.
2 мысал. Жәшікте 3 ақ және 2 қара шар бар. Қалай болса солай жәшіктен бір шар алынған. Ақ шар алу ықтималдығы
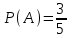 . Шарды қайтадан жәшікке салып, тәжірибені қайталайды. Екінші тәжірибеде де жәшіктен ақ шар алу ықөтималдығы
. Шарды қайтадан жәшікке салып, тәжірибені қайталайды. Екінші тәжірибеде де жәшіктен ақ шар алу ықөтималдығы 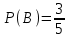 -ке тең және ол бірінші тәжірибенің нәтижесінде тәуелді емес. Бұл жағдайда да А және В тәуелсіз оқиғалар.
-ке тең және ол бірінші тәжірибенің нәтижесінде тәуелді емес. Бұл жағдайда да А және В тәуелсіз оқиғалар.3 мысал.Жәшікте 3 ақ, 2 қара шар бар. Жәшіктен бірінен соң бірі екі шар алынған. Бірінші тәжірибеде ақ шар алу ықтималдығы
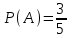 . Екінші рет ақ шар алу ықтималдығы
. Екінші рет ақ шар алу ықтималдығы 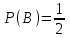 бірінші тәжірибенің ықтималдығына тәуелді. Бұл мысалда А мен В тәуелді оқиғалар. Егер бірнеше оқиғалардың әрбір екеуі өзара тәуелсіз болса, онда оларды қос-қостан тәуелсіз оқиғалар деп атайды.
бірінші тәжірибенің ықтималдығына тәуелді. Бұл мысалда А мен В тәуелді оқиғалар. Егер бірнеше оқиғалардың әрбір екеуі өзара тәуелсіз болса, онда оларды қос-қостан тәуелсіз оқиғалар деп атайды.