4 мысал. Теңге 3 рет лақтырылған. А,В,С арқылы бірінші, екінші және үшінші тәжірибелердегі сәйкес «гербтің пайда болуын белгілейік. Бұл үш оқиғаның әрбір екеуі (А мен В, А мен С, В мен С) тәуелсіз. Олай болса, А,В және С оқиғалары қос-қостан тәуелсіз.

2. 
   Тәуелсіз оқиғалардың ықтималдықтарын көбейту теоремасы
   

Кездейсоқ оқиғаларды көбейту (үйлестіру)

А және В екі кездейсоқ оқиғаның бірге пайда болуынан тұратын оқиғаны осы екі оқиғаның көбейтіндісі деп атайды да, АВ арқылы белгілейді.



Теорема: Бірге пйда болған екі тәуелсіз оқиғаның ықтималдығы ол оқиғалардың ықтималдықтарының көбейтіндісіне тең:



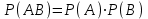
Салдар: Жиынтығы тәуелсіз болатын бірнеше оқиғалардың пайда болу ықтималдығы ол оқиғалардың ықтималдықтарының көбейтіндісіне тең:



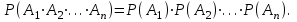
Мысалдар.1. Апатты хабарлау үшін бір біріне тәуелсіз жұмыс істейтін екі сигналдаушы орнатылған. Апат кезінде сигналдаушының жұмыс істеу ықтималдығы бірінші сигналдаушы үшін 0,95-ке, ал екінші үшін 0,9-ға тең. Апат кезінде екі сигналдаушының да жұмыс ықтималдығын табу керек.

Шешуі. А оқиғасы-апат кезінде бірінші сигналдаушы жұмыс істейді. В оқиғасы-екінші сигналдаушы жұмыс істейді. Бұл оқиғалардың сәйкес ықтималдықтары Р(А)=0,95; Р(В)=0,9

А мен В оқиғалары өзара тәуелсіз, сондықтан олардың бірге пайда болу ықтималдығы мынаған тең:



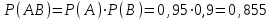
2. Студент керек формуланы 3 анықтамадан іздейді. Формуланың бірінші, екінші және үшінші анықтамада болу ықтималдығы, сәйкес 0,6; 0,7; 0,8-ге тең. Мына оқиғалардың ықтималдықтарын есептеңіздер: формула: а) үш анықтамада да бар; б) тек бір анықтамада ғана бар; в) тек екі анықтамада бар.

Шешуі.А оқиғасы-формула бірінші анықтамада бар; В оқиғасы-формула екінші анықтамада бар; С-үшінші анықтамада бар.

Олардың ықтималдықтары



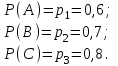
А,В,С оқиғаларына кері (қарама-қарсы) оқиғалар, сәйкес 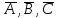арқылы белгіленеді, олардың ықтималдықтары: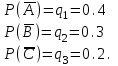



а) Керек формула анықтамалардың үшеуінде де бар болу ықтималдығы тәуелсіз оқиғалар ықтималдықтарын көбейту формуласы бойынша мынаған тең:

---

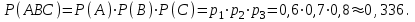
б) Керек формула тек бір анықтамада ғана бар. Мынадай күрделі оқиғалардың пайда болуы мүмкін:



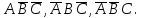
Бұл оқиғалар үйлесімсіз, сондықтан оларға қосу теоремасы қолданылады. Ізделінді ықтималдық:



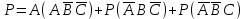
Осы ықтималдықтарды есептейміз. А, В, С өзара оқиғалар, сондықтан оларға кері оқиғалар -да тәуелсіз, ендеше бұл оқиғалардың әртүрлі комбинациялары да тәуелсіз болады, онда бұларға көбейту теоремасы қолданылады.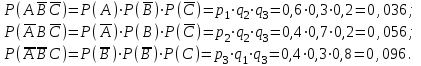



Ізделінді ықтималдық:

Р=0,036+0,056+0,096=0,188.

в) Керек формула тек екі анықтамада бар, бұл жағдайда мынадай күрделі оқиғалар болуы мүмкін:



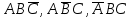
Олардың ықтималдықтары:



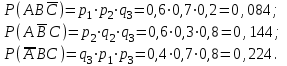
Ізделінді ықтималдық:



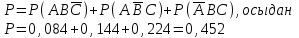
Жауабы: а) 0,336; б) 0,188; в) 0,452.

Құрастырушыға қажет детальдің бірінші, екінші, үшінші, төртінші жәшікте болу ықтималдығы сәйкес 0,6; 0,7; 0,8; 0,9-ға тең. Мына оқиғалардың ықтималдықтарын есептеңіздер: қажет деталь болуы мүмкін жәшіктер саны: а) 3-тен аспайды; б) екіден кем емес.

Шешуі. А₁-қажет деталь бірінші жәшікте; А₂- қажет деталь екінші жәшікте; А₃-үшінші жәшікте; А₄-төртінші жәшікте. Олардың ықтималдығы:



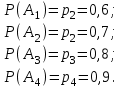
А₁, А₂, А₃, А₄ оқиғаларына кері оқиғаларды 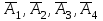арқылы белгілесек, олардың ықтималдығы:

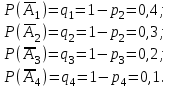болады.

а) Қажет деталь болу мүмкін жәшіктер саны 3-тен аспайды, яғни деталь 4 жәшіктің: 1) тек біреуінде ғана болуы мүмкін, қайсысында болса да бәрібір, немесе 2) тек екеуінде; 3) тек үшеуінде болуы мүмкін. Бұл үш жағдайда сәйкес мынадай күрделі оқиғалар орын алады:

1) 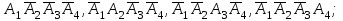оқиға саны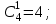

2)

---

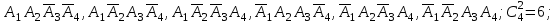
3)

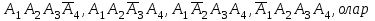
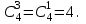
Бұл күрделі оқиғалар 3 жағдайдың әрбіреуінде өзара үйлесімсіз (егер тәжірибе бір рет қана жасалса). 3 жағдай бір бірімен тағы да үйлесімсіз, сондықтан олардың ықтималдықтарына қосу теоремалары қолданылады. Ал әр күрделі оқиғаны құраушы оқиғалар өзара тәуелсіз, сондықтан олардың ықтитмалдықтарына көбейту теоремасы қолданылады. Қажет деталь тек бір жәшікте деген тұжырымының ықтмалдығы



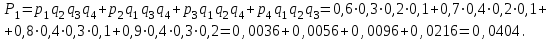
Қажет деталь тек екі жәшікте, қайсысында болса да бәрібір, болуы мүмкін ықтималдығы



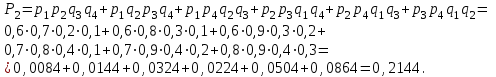
Қажет деталь тек үш жәшікте болу ықтималдығы



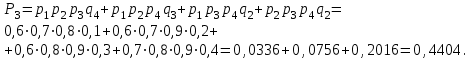
Ізделінді ықтималдық

Р=Р₁+Р₂+Р₃=0,0404+0,2144+0,4404=0,6952.

б) Қажет деталь болу мүмкін жәшіктер саны 2-ден кем емес деген ұғым, деталь: 1) не екі жәшікте; 2) не үш жәшікте; 3) не 4 жәшікте бар дегенмен бара бар. Алғашқы екі оқиғаның ықтималдықтары Р₂ және Р₃ есептелді, ал үшінші оқиға Р₄ болу үшін мына күрделі оқиға А₁А₂А₃А₄ орындалуы керек. Бұл күрделі оқиғаны құраушы оқиғалар өзара тәуелсіз, ендеше оларға көбейту теоремасы қолданылады.



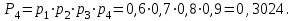
Ізделінді ықтималдық



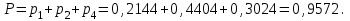
11. Ықтималдықтарды қосу және көбейту теоремалары. Салдарлары.Анықтамасы. Мысал келтіріңіз.

12. Ең болмаганда бір оқиғаның пайда болуының ықтималдығын анықтау. Салдарлары. Мысал келтіріңіз.

Тәжірибе нәтижесінде жиынтығы тәуелсіз болатын n оқиға пайда болуы, немесе олардың кейбіреуі ғана пайда болуы мүмкін. Дербес жағдайда тек бір оқиға пайда болуы, немесе бірде біреуі пайда болмауы мүмкін. Осы оқиғалардыыың кем дегенде біреуінің пайда болу ықтималдығы қалай табуға болады? Мысалға, тәжірибе нәтижесінде 3 оқиға пайда болуы мүмкін болса, онда олардың кем дегенде біреуінің пайда болуы, не бір оқиғаның, не екі оқиғаның, немесе үш оқиғаның пайда болуын көрсетеді. Мына теореманы қарастырайық:

Теорема: Жиынтығы тәуелсіз болатын А₁, А₂, ..., А_n оқиғаларының кем дегенде біреуінің пайда болу ықтималдығы Р(А):1 саны мен

---

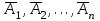кері оқиғалардың ықтималдықтарының көбейтіндісінің айырымына тең: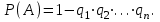



Дербес жағдай. Егер А₁, А₂, ..., А_n оқиғаларының пайда болу ықтималдықтары бірдей, р-ға тең болса, онда осы оқиғалардың кем дегенде біреуінің пайда болу ықтималдығы Р(А) мына формуламен есептелнеді:

Р(А)=1-qⁿ

Мысалдар.1. үш зерттеуші, бір-бірімен байланыссыз, кейбір физикалық шаманы өлшеумен айналысады. Бірінші зерттеушінің, прибордың көрсетуін салыстырып оқу кезінде, қате жіберу ықтималдығы 0,1-ге тең, ал екінші және үшінші зерттеуші үшін бұл ықтималдық сәйкес 0,15 пен 0,2-ге тең. Бір рет өлшеу кезінде үш зерттеушінің кем дегенде біреуінің қате жіберетігіндігінің ықтималдығын есептеу керек.

Шешуі.А-өлшеу кезінде кем дегенде бір зерттеуші қате жібереді. А₁-бірінші зерттеуші қате жібереді; А₂-екінші зерттеуші қате жібереді; А₃-үшінші зерттеуші қате жібереді. Олардың ықтималдығы: Р(А₁)=р₂=0,1; Р(А₂)=р₂=015; Р(А₃)=р₃=0,2, ендеше кері оқиғалардың (өлшеу кезіндегі зерттеушілердің қате жібермеунің) ықтималдықтары сәйкес q₁=0,9; q₂=0,85; q₃=0,8 болады. Ізделінді ықтималдық P(A)=1-q₁q₂q₃=1-0,612=0,388.

2. Таңдамай алынған астықтың бір дәнінен 50-ден кем емес дәні бар масақ өсіріп шығару ықтималдығы 0,6-ға тең. Қалай болса солай алынған 10 дәннен, ішінде 50-ден кем болмайтын дәні бар, ең болмағанда бір масақ өсіп шығу ықтималдығы қандай?

Шешуі. А-10 дәннен, ішінде 50-ден кем болмайтын дәні бар, ең болмағанда бір масақ өсіп шығады. Дәннің шығымдылық қабілеті-0,6, яғни р=0,6; q=1-p=0,4; n=10 онда

Р(А)=1-qⁿ=1-0,4¹⁰≈0,9999.

3. Атқыштың бір рет атқанда нысанаға оқ тигізу ықтималдығы 0,3-ке тең. 0,7599-дан кем болмайтын ықтималдықпен ең болмағанда бір рет нысанаға тигізу үшін атқыш неше рет оқ ату керек?

Шешуі.А-рет оқ атқанда атқыш кем дегенде бір реет нысанаға тигізеді. Бірінші, екінші және одан кейінгі атқандарында «нысанаға оқ тигізу» оқиғалары-жиынтығы олардың ықтималдықтарын ессептуге

Р(А)=1-qⁿ

формуласын қолданады. Есептің шарты бойынша Р(А)0,7599, р=0,3, ендеше q=1-p=0,7. осы мәндерді жоғары формулаға қойсақ 1-0,7ⁿ0.7599, осыдан 0,7ⁿ0,2401, немесе 0,7 ⁿ0,7⁴. Олай болса n4.

Сонымен, есептің шарты орындалу үшін атқыш нысанаға 4 реттен кем оқ атпау керек.

4.Нысанаға 4 рет атқанда кем дегенде бір рет оқ тигізу ықтималдығы 0,9984-ке тең. Бір рет атқанда нысанаға оқ тигізу ықтималдығы қандай?

---

Шешуі. Әрбір атқанда нысанаға оқ тигізу мүмкіндігі тәуелсіз болғандықтан

Р(А)=1-qⁿ

формуласы қолданылады. Мұндағы

Р(А)=0,9984;n=4

Ендеше 0,9984=1-qⁿ немесе

q⁴=1-0,9984=0,0016

Осыдан

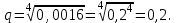
Ізделінді ықтималдық

р=1-q=1-0,2=0,8.


13. Толық ықтималдықтың формуласы. Байес формуласы. Мысал келтіріңіз.

---

Смотрите также файлы

• 3. Распределение заданий по проверяемым предметным способам действия.docx

• Е. Ж. Васильев 2017 г.docx

• .docx

• Урока Предмет Класс Тема урока Планируемые образовательные результаты Предметные.docx

• Решение ситуационных задач по теме Антигипертензивные средства.docx