Файл: Системы координат, применяемые в динамике полета.doc

Сделать презентацию

Скачать файл (2,85Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 298

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Введение.При проектировании систем стабилизации и управления летательных аппаратов важным этапом является выявление динамических свойств летательного аппарата (ЛА) как объекта управления. Имеется обширная отечественная и зарубежная литература, посвященная построению математической модели динамики движения летательного аппарата.Настоящие методические указания облегчают работу с этой литературой, дают рациональные приемы вывода уравнений движения ЛА и их линеаризации.§ 1. Системы координат, применяемые в динамике полета.Задачи динамики полета самолетов и ракет рассматриваются обычно в топоцентрической системе отсчета. Начало топоцентрической системы координат помещается в пункте наблюдения, в частности, на поверхности земного шара. Эта система используется в тех случаях, когда рассматривается движение по отношению к поверхности Земли.I. Земная система координат.Частный случай топоцентрической системы координат – земная система координат. Земных координат несколько. За начало земной системы прямоугольных координат можно принимать центр масс Земли, точку старта или другую неподвижную относительно Земли точку. Выберем земную систему координат следующим образом (рис. 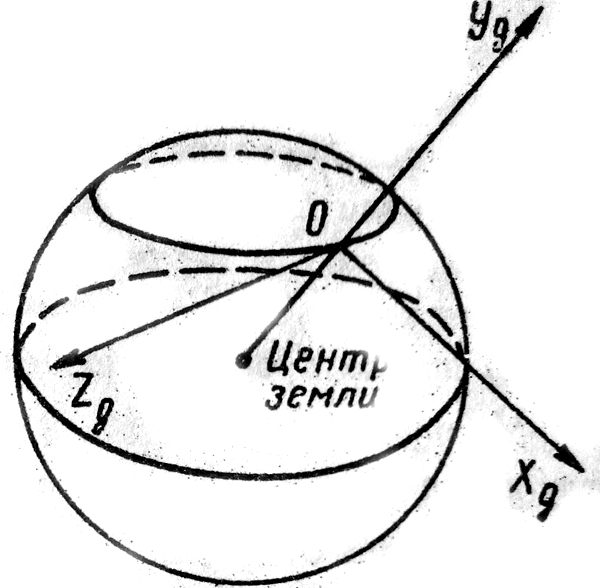1).Рис. 1. Земная система координатОсь OY_g – прямая, соединяющая центр Земли с точкой старта на её поверхности. Ось OX_g перпендикулярна оси OY_g и лежит в вертикальной плоскости прицеливания или начального движения ЛА в момент старта. Ось OZ_g дополняет систему до правой. Такая система координат называется нормальной земной системой координат OX_gY_gZ_g. Часто начало координат нормальной земной системы помещают в центре масс ЛА, а направление её осей совпадает с начальным направлением этих осей в момент старта. Таким образом, определяется нормальная система координат OX_gY_gZ_g, а её оси в данном случае совпадают также с осями стартовой системы OX_cY_cZ_c. В дальнейшем нормальную систему будем обозначать индексом g.Задав оси системы координат, можно выбрать базис, в котором любой вектор запишется так: ,где

, , – единичные векторы.

II. Связанная система координат
Начало связанной системы координат (рис. 2) помещают в центре масс ЛА, который будем считать неподвижным относительно корпуса ЛА. Ось OX направлена вдоль строительной оси корпуса ЛА вперед. Ось OY располагают в той плоскости симметрии ЛА, которая в момент пуска совпадает с плоскостью стрельбы. Ось OY перпендикулярна оси OX и направлена вверх. Ось OZ дополняет систему до правой. Связанная система координат неподвижна относительно корпуса ЛА. Обозначать её будем индексом I.

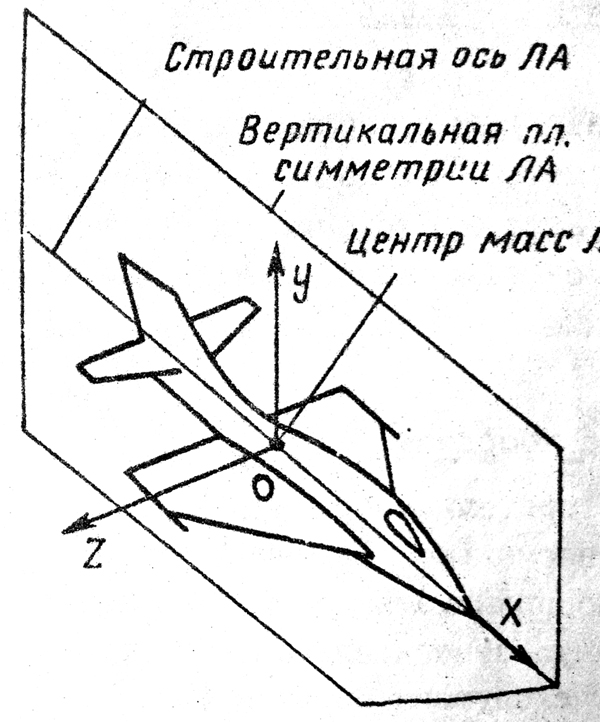
Рис. 2. Связная система координат
III. Скоростная система координат
В скоростной системе координат (рис. 3) ось OX_a совпадает с направлением вектора скорости полёта центра масс ЛА и закреплена в центре масс, ось OY_a перпендикулярна ей, лежит в вертикальной плоскости симметрии ЛА и направлена вверх. Ось OZ_a перпендикулярна осям OX_a и OY_a и дополняет их до правой тройки. Скоростую систему будем обозначать индексом a.
IV. Траекторная система координат
В траекторной системе координат (рис. 4) ось OX_k, как и в скоростной, совпадает с направлением вектора скорости, ось OY_k направлена перпендикулярно ей и лежит в местной вертикальной плоскости, ось OZ_k перпендикулярна первым двум, лежит в горизонтальной плоскости и направлена в сторону правого крыла.

Траекторную систему обозначим индексом k.

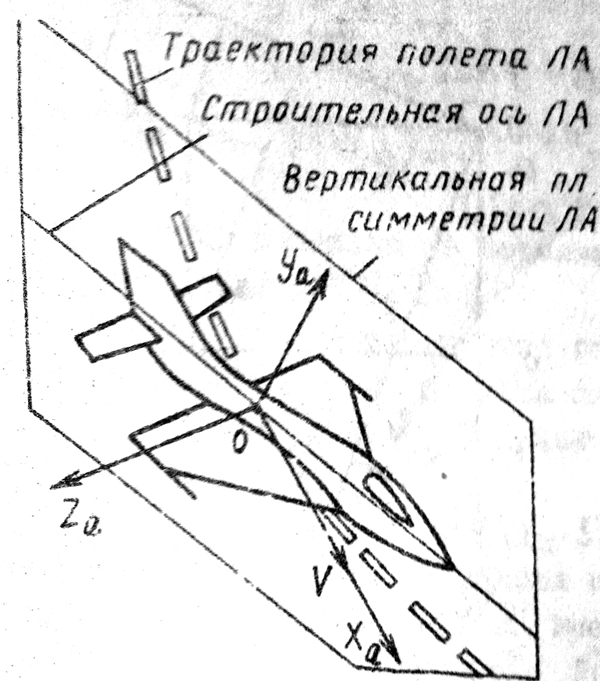
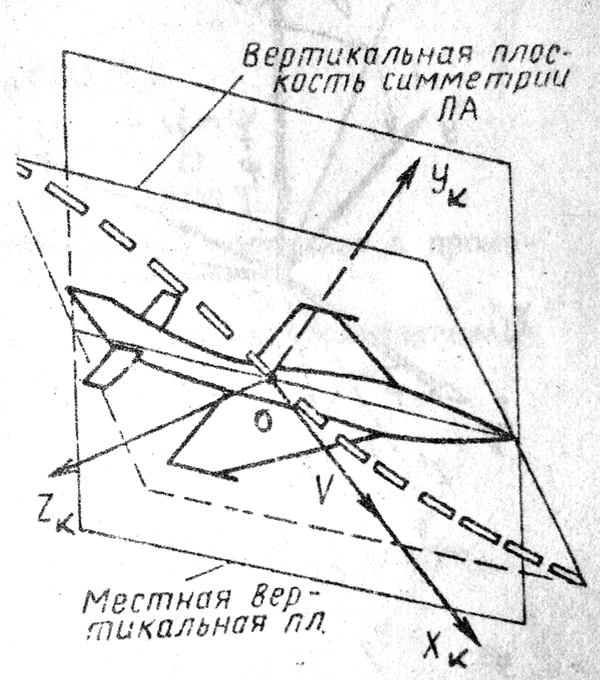
Рис. 3. Скоростная система координат Рис. 4. Траекторная система координат

§ 2. Связь между системами координат
Определенные в § 1 системы координат являются ортогональными, поэтому переход из системы координат A в систему координат B характеризуется ортогональным преобразованием

Для ортогональных матриц справедливо:

;

1. Как видно из рис. 5, связанная и нормальная системы связаны между собой через углы Эйлера.Обычно принимается следующий порядок поворота координатных осей.1) Поворот вокруг оси OY_g на угол – угол рыскания. Это угол между проекцией связанной оси OX на местную горизонтальную плоскость и направлением оси OX_g нормальной системы.2) Поворот на угол – угол тангажа. Это угол между направлением связанной оси OX и местной горизонтально плоскостью.3) Поворот на угол – угол крена. 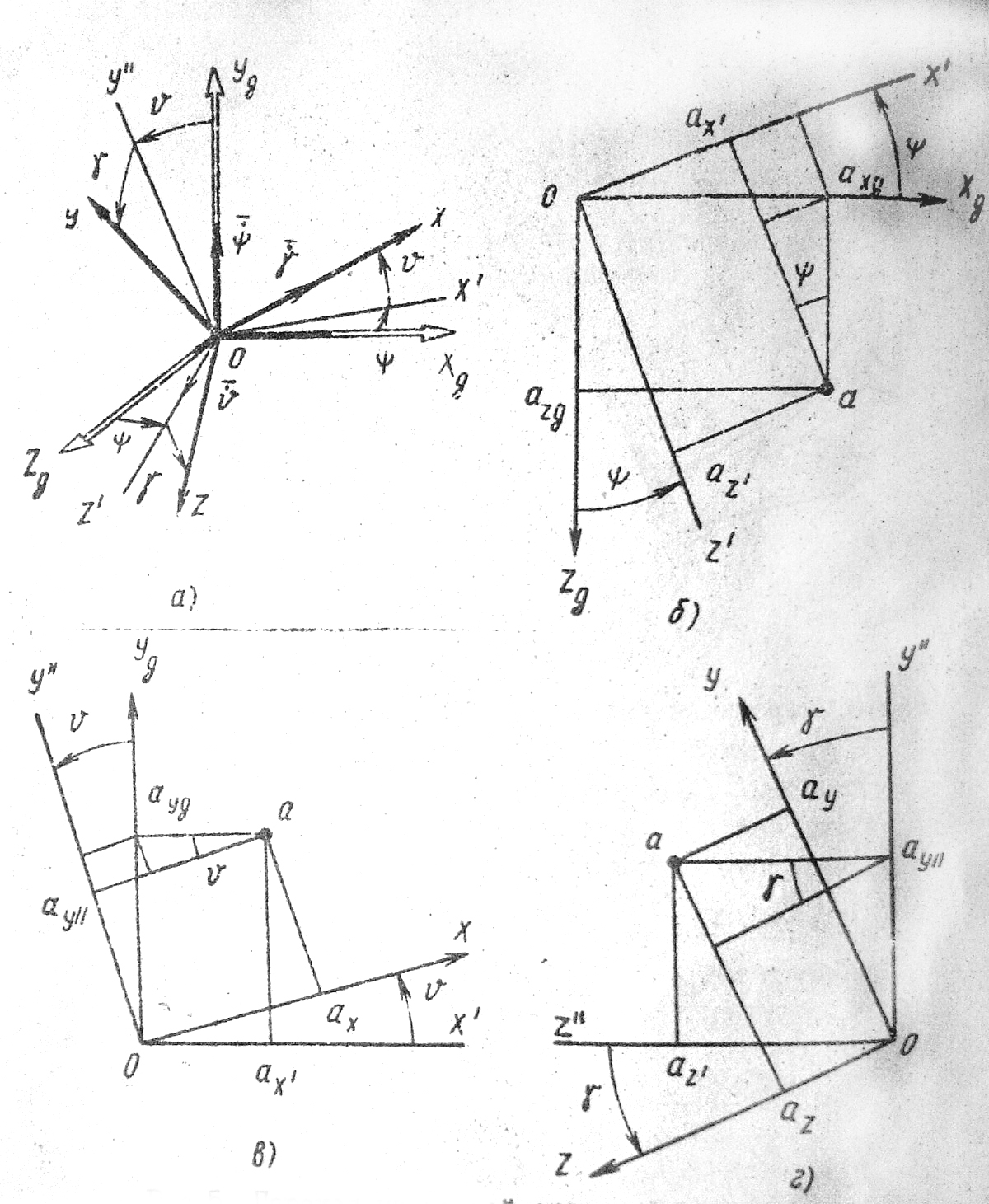Это угол между вертикальной плоскостью симметрии ЛА и местной вертикальной плоскостью, содержащей ось OX.Рис. 5. Переход из земной системы координат в связанную.Найдем матрицу T(1,g) перехода из нормальной системы координат в связанную (рис. 5а). Первый поворот происходит в плоскости OX_gY_g на угол . Из рис. 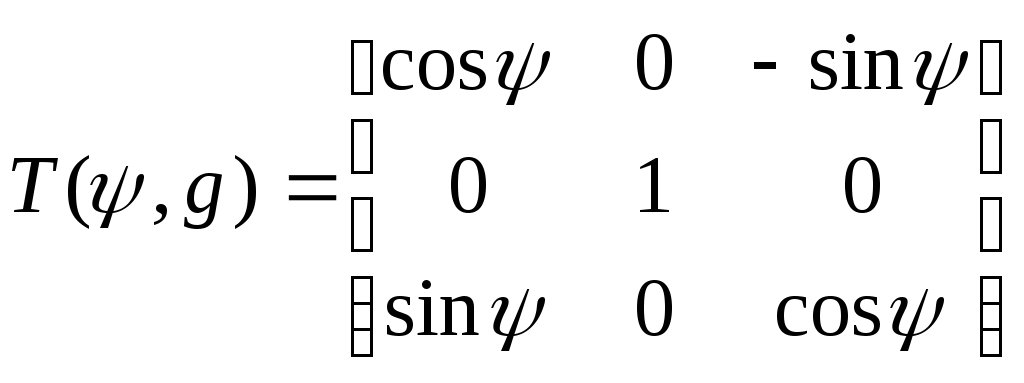5б видно: ; ; .Таким образом,– это матрица перехода из нормальной системы координат в промежуточную систему OX'Y_gZ'.На рис. 5в иллюстрируется второй поворот на угол тангажа в плоскости OX'Y_g. Из рисунка следует, что ; ; ;Таким образом, матрица перехода из системы OX'Y_gZ' во вторую промежуточную систему OXY''Z' имеет вид 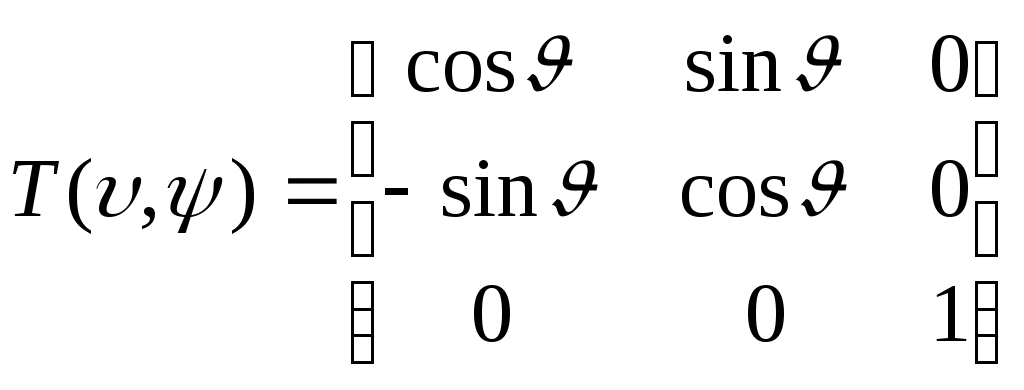.И, наконец, поворот на угол крена

вокруг оси OX приводит к переходу в связанную систему координат (рис. 5г):

;

.

Матрица перехода из системы OXY''Z' в систему OXYZ имеет вид:

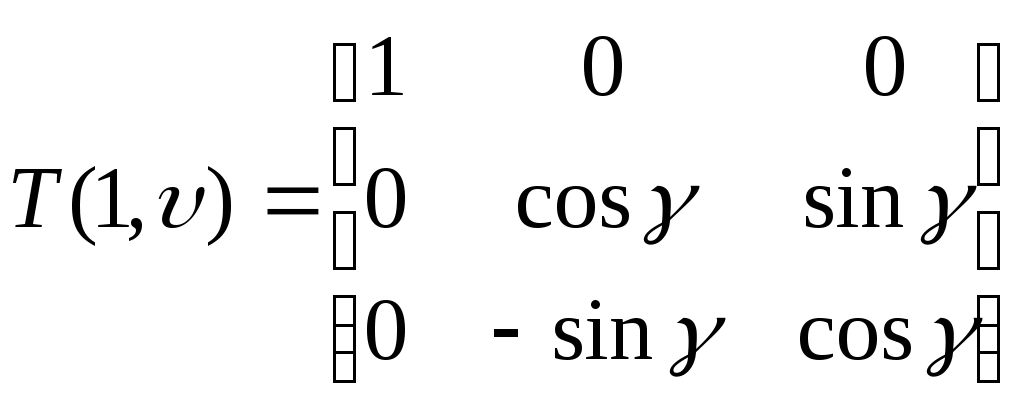
Найдем искомую матрицу: ,

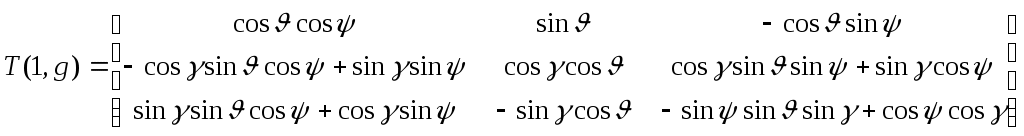
2. Скоростная и нормальная системы координат (рис. 6) связаны между собой через три угла Эйлера, которые перечислены в порядке последовательности поворотов:

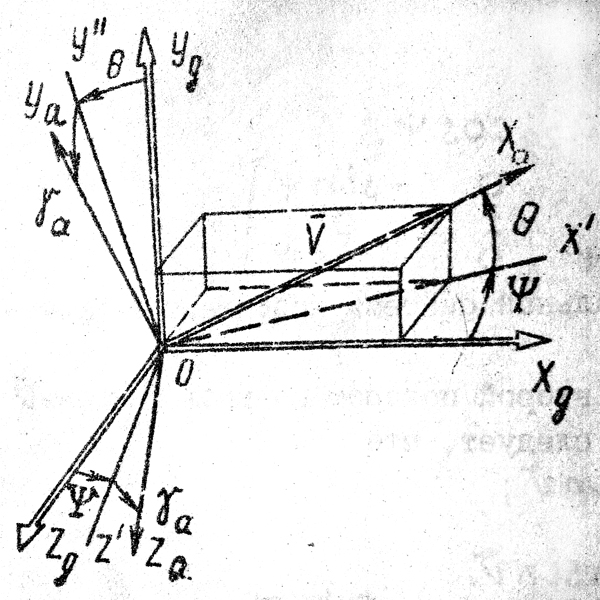
Рис. 6. Переход из нормальной системы координат в скоростную
– угол пути, или угол поворота траектории ЛА. Это угол между проекцией вектора скорости на местную горизонтальную плоскость и осью OX_g нормальной системы координат;

– угол наклона к горизонту касательной к траектории ЛА (угол между вектором скорости и местной горизонтальной плоскостью). Угол называют углом наклона траектории;

– угол крена в скоростной системе координат.

Нетрудно видеть, что матрицу перехода из нормальной системы координат в скоростную T(a,g) можно получить из известной уже матрицы T(1,g) путём соответственной замены углов , и на , и

:

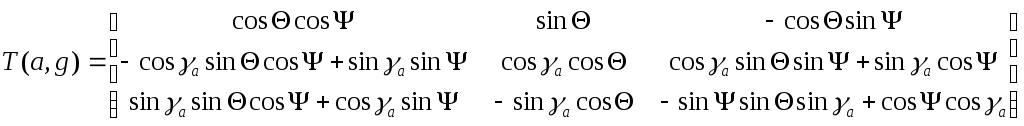
3. Траекторную систему координат можно получить из нормальной с помощью двух последовательных поворотов на углы и .

Матрицу перехода из нормальной в траекторную систему координат T(k,g) можно получить из матрицы T(a,g), положив в ней

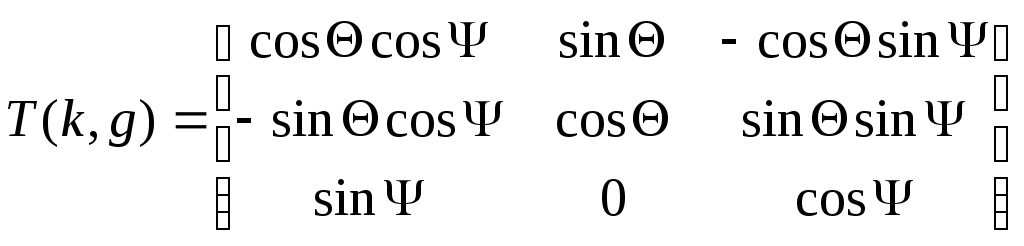
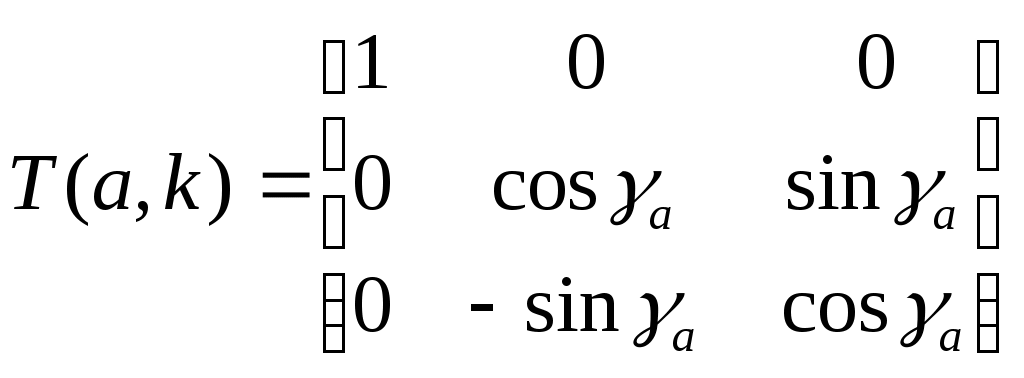
А матрицу перехода с траекторной системы к скоростной T(a,k) получим как матрицу третьего поворота на угол при переходе из нормальной системы к связанной, заменив в ней на :

4. Связанная система координат может быть получена из скоростной системы координат с помощью двух последовательных поворотов – на углы и (рис. 7).

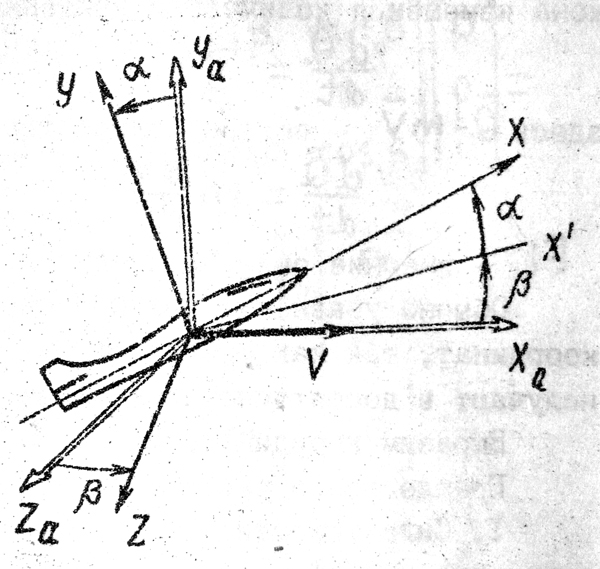
Рис. 7. Переход из скоростной системы в связанную

– угол скольжения между вектором скорости и его проекцией на вертикальную плоскость симметрии ЛА; – угол атаки, это угол между осью OX связанной системы координат и проекций скорости на плоскость OXY.

Матрицу T(1,a) перехода из скоростной системы координат в связанную, запишем так же, как и матрицу T(k,g) перехода из нормальной системы в траекторную, заменив в последней углы и на