ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 90
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и  :
:
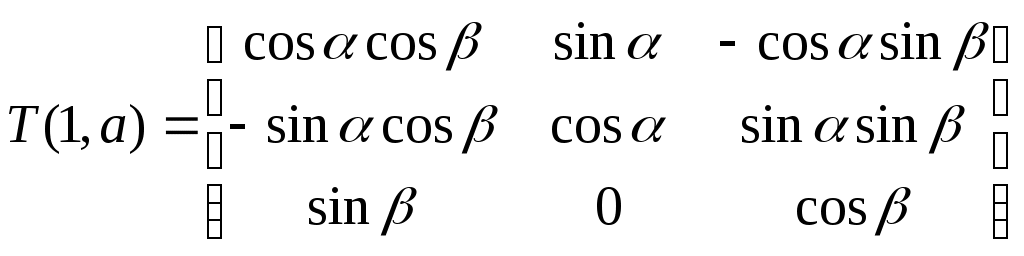
Подробная классификация систем координат и матриц перехода из одной системы в другую дана в [2].
В рекомендуемой литературе [1]-[5] все определения и обозначения даны в соответствии с ГОСТ 1075-41. Для облегчения перехода от системы обозначений ГОСТ 1075-41 к принятой в настоящее время системе ГОСТ 20058-74 следует пользоваться.
§ 3. Дифференциальные уравнения движения летательного аппарата
При выводе уравнений движения ЛА делает следующие допущения:
1. ЛА рассматривается как абсолютно твёрдое тело переменной массы, имеющие 6 степеней свободы.
2. Моменты инерции ЛА постоянны.
3. ЛА имеет вертикальную плоскость симметрии.
3. Не учитываются влияние ветра, сферичность и вращение земли.
Уравнения движения центра масс ЛА получим основании закона изменения количества движения центра масс:
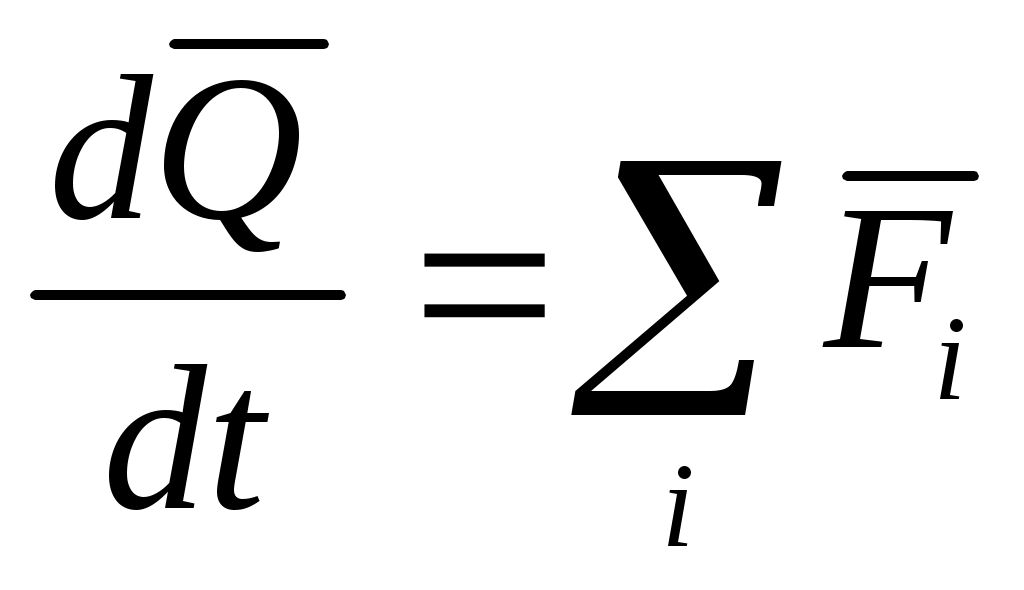 ,
,
Здесь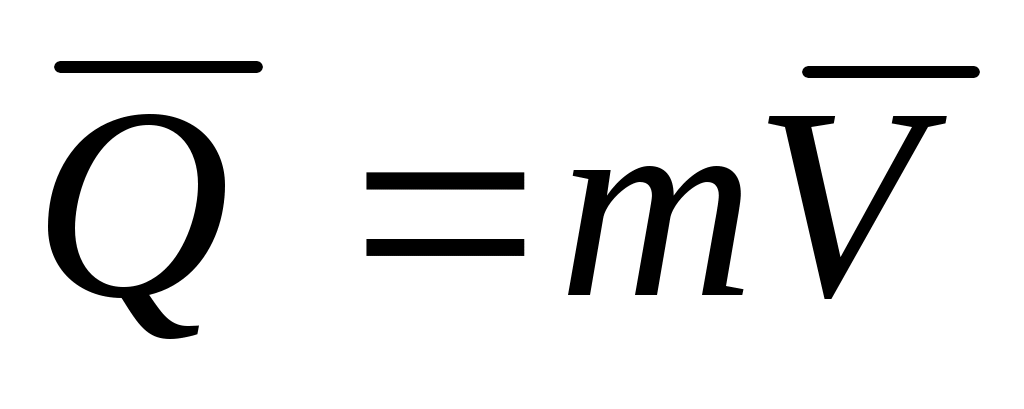 – вектор количества движения ЛА,
– вектор количества движения ЛА,
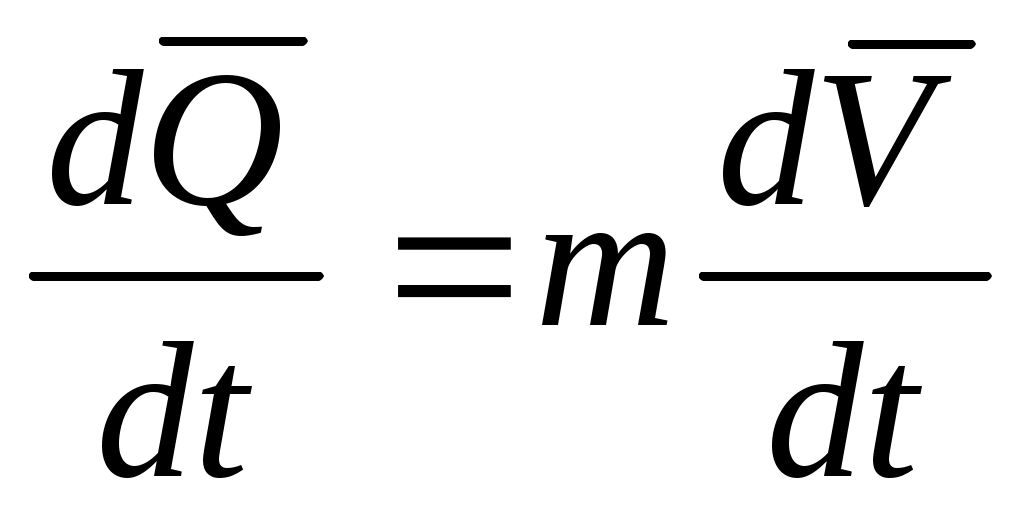 ;
;
Fi – внешние силы, действующие на ЛА.
Обычно уравнения сил проецируют на оси траекторной системы координат, так как в это случае Vx=V, Vy=Vz=0 и уравнения получают в достаточно простом виде.
Выразим координаты всех сил в базисе траекторной системы.
Прежде всего рассмотрим эти силы.
1. Сила тяжести. Поскольку эта сила направлена по местной вертикали, её обычно задают в базисе нормальной системы координат:
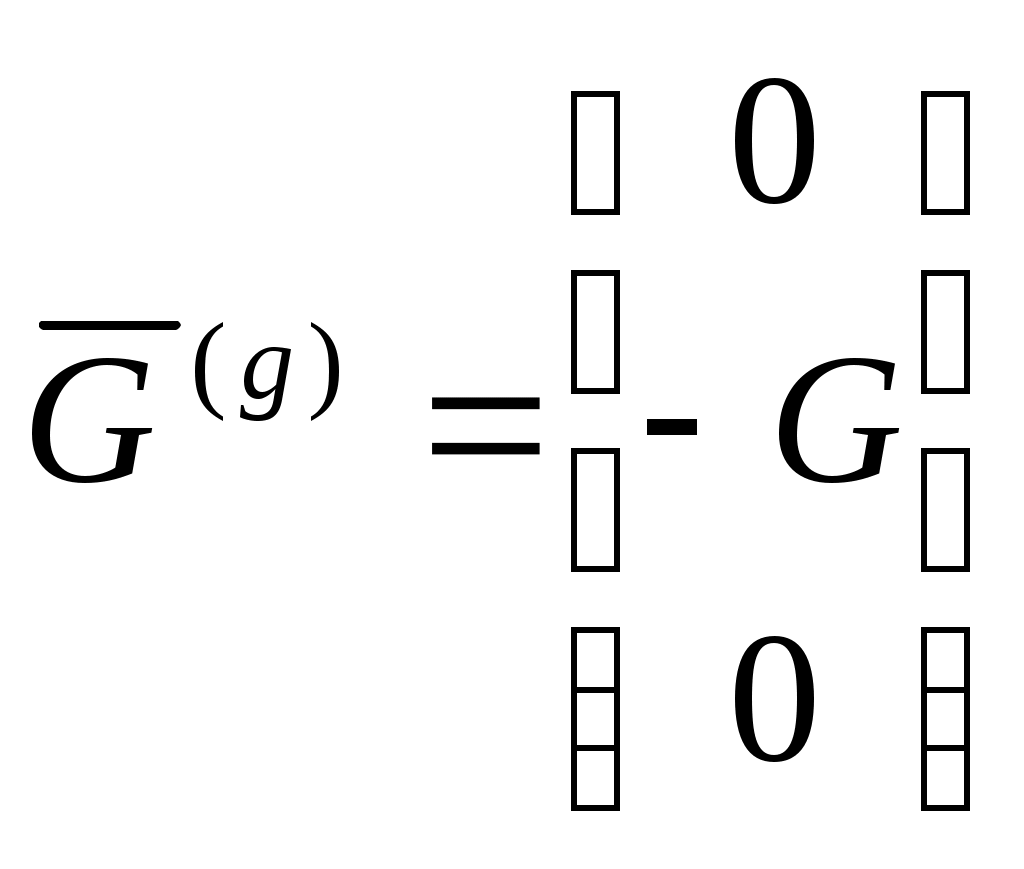
2. Сила тяги двигателя приложена в центре масс двигателя и направлена по оси OX связанной системы. Она задается в базисе связанной системы координат:
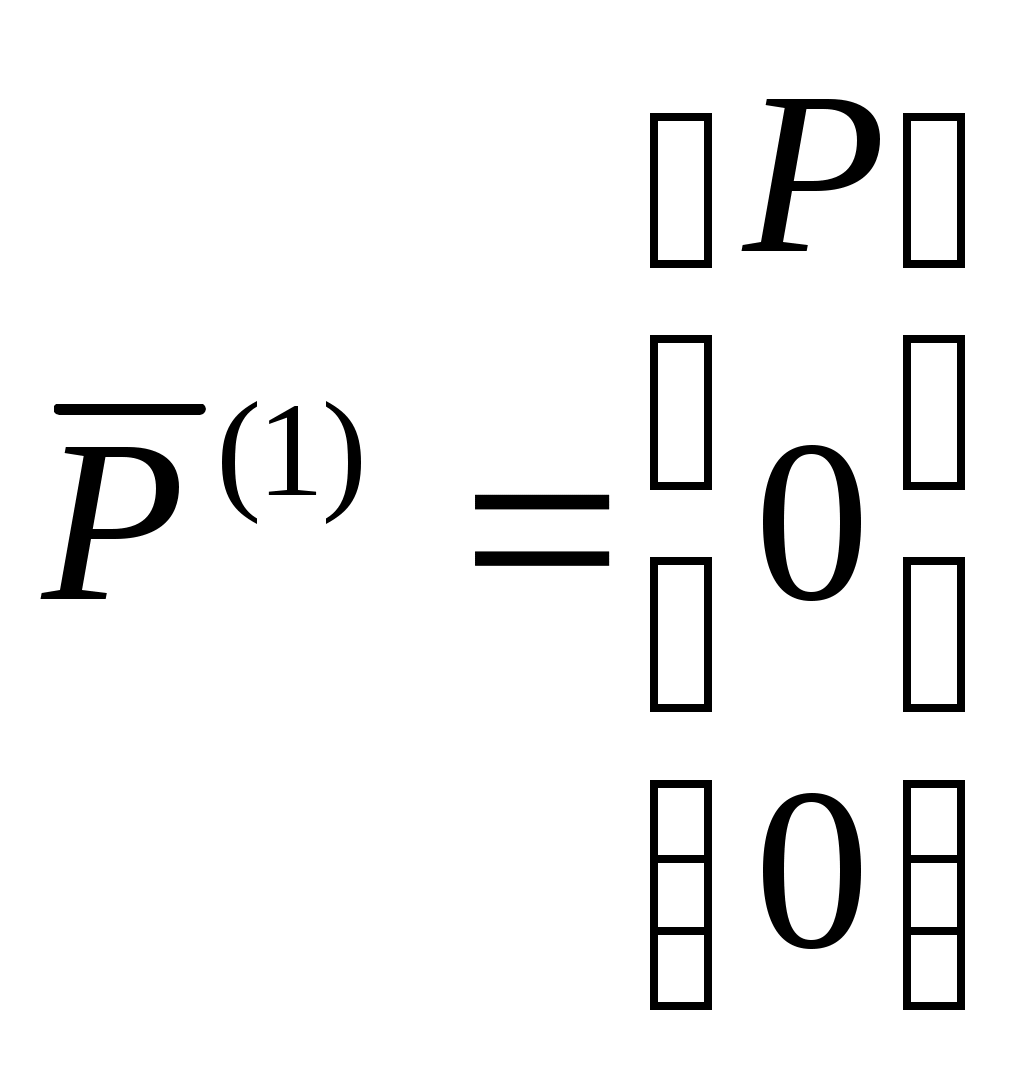
3. Равнодействующая аэродинамических сил обычно записывается в базисе скоростной системы:
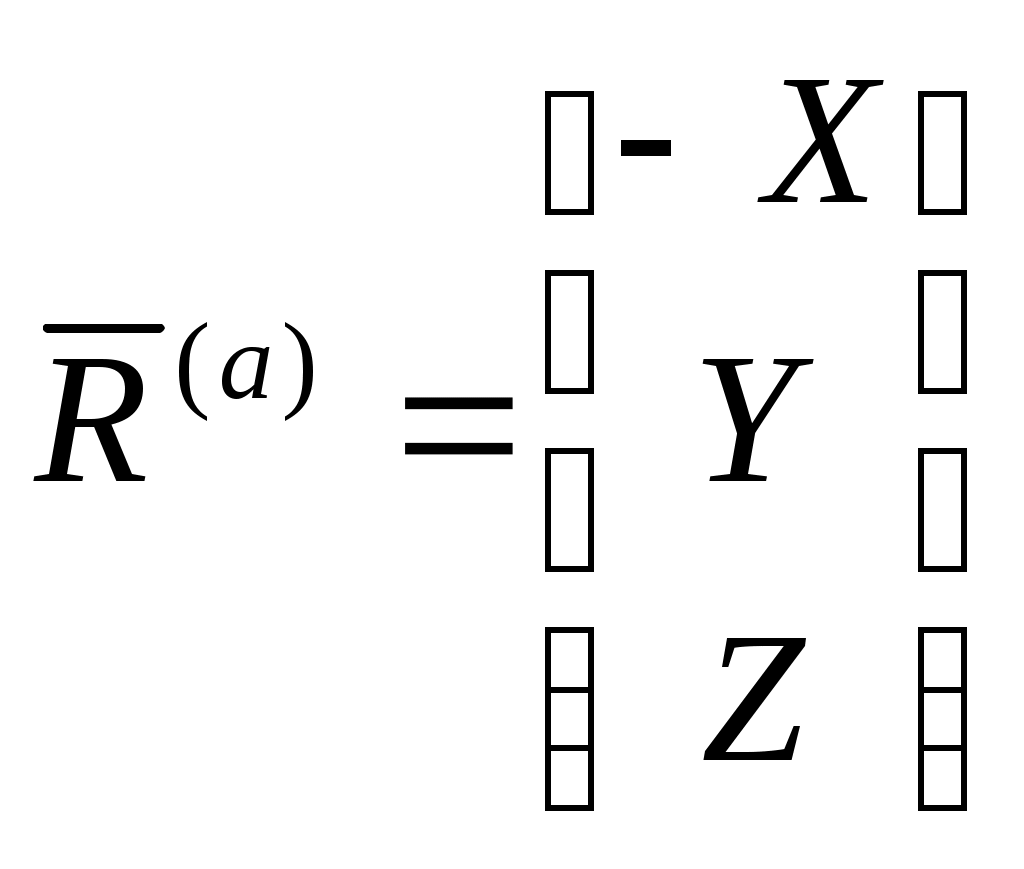
где X – сила лобового сопротивления;
Y – подъемная сила;
Z – боковая сила.
Запишем эти силы в проекциях на оси траекторной системы:
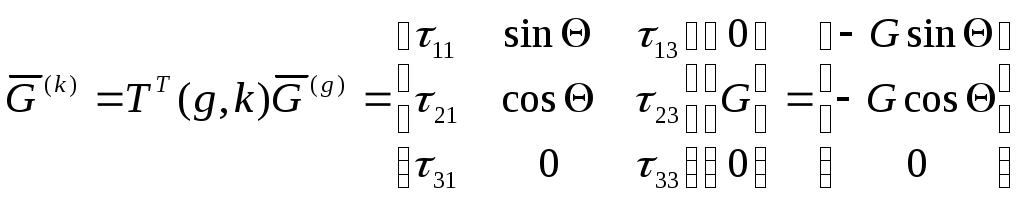
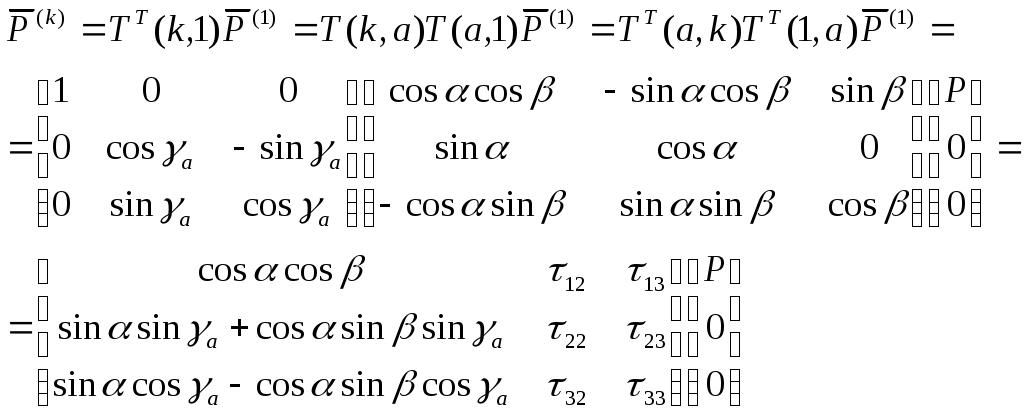
Окончательно
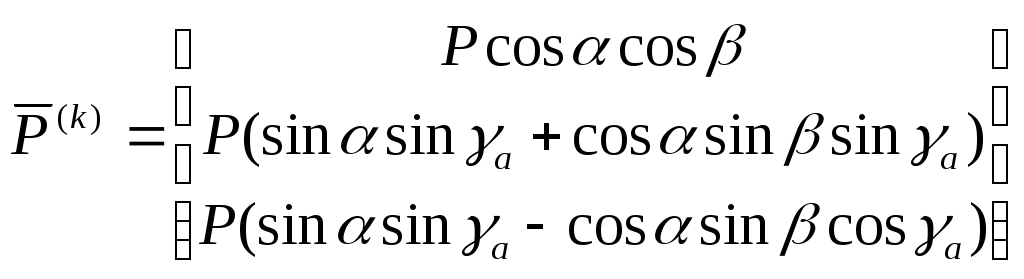
Аэродинамические силы выразятся так:
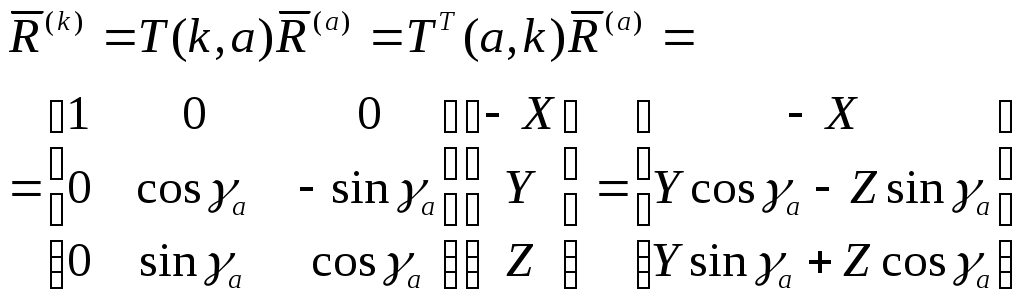
Поскольку проекции вектора скорости в скоростной и траекторной системах координат совпадают, то запишем левую часть уравнения сил в базисе траекторной системы:
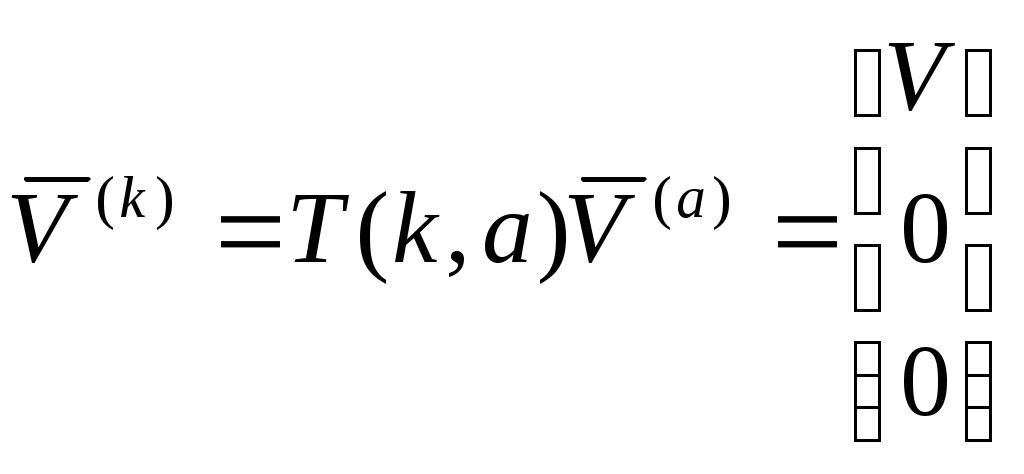
Дифференцируем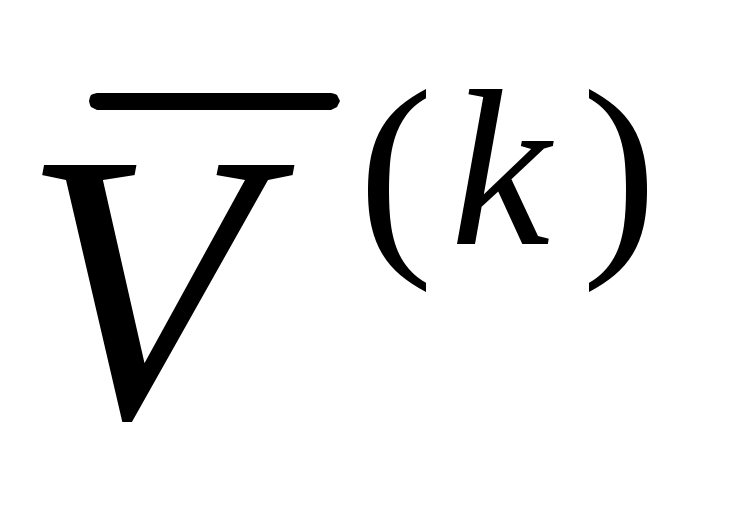 по правилам дифференцирования вектора, записанного в подвижном базисе:
по правилам дифференцирования вектора, записанного в подвижном базисе:
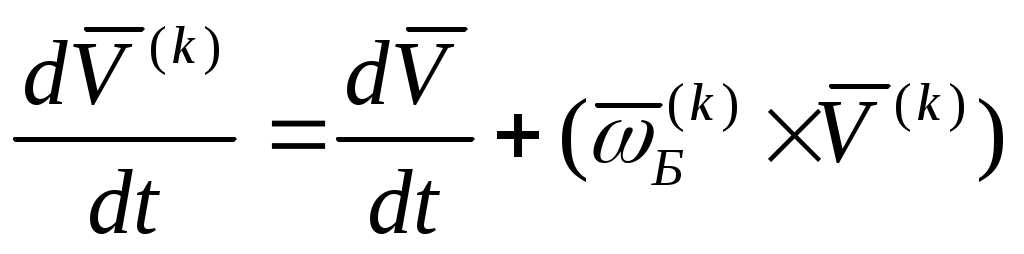 ,
,
где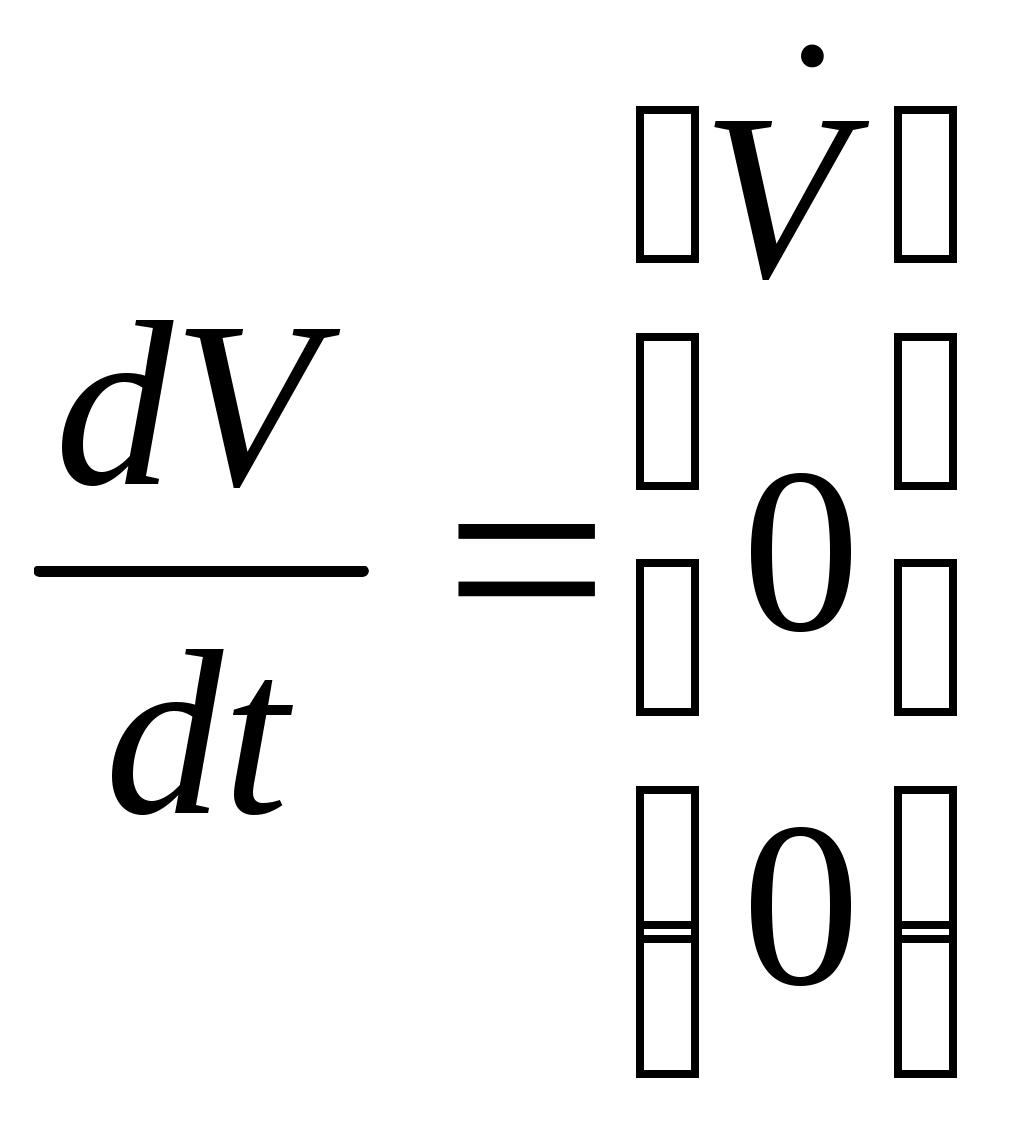 – локальная производная по времени, взятая в предположении неподвижого базиса;
– локальная производная по времени, взятая в предположении неподвижого базиса; 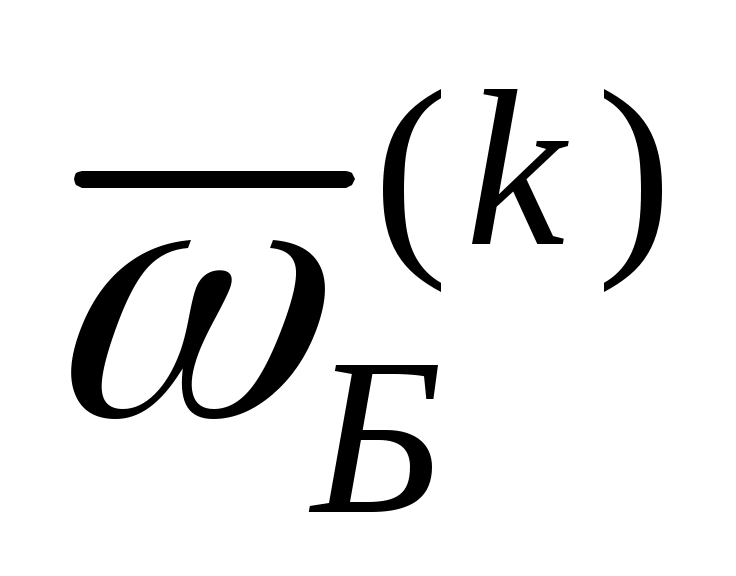 – угловая скорость вращения базиса.
– угловая скорость вращения базиса.
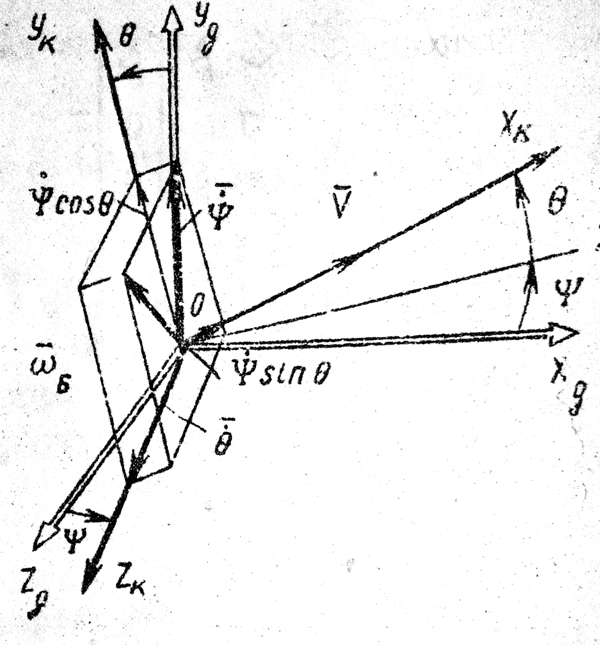
Рис. 8. Вращение базиса траекторной системы координат в нормальной.
Обратимся к рис. 8. Нетрудно видеть, что вектор угловой скорости траекторной системы координат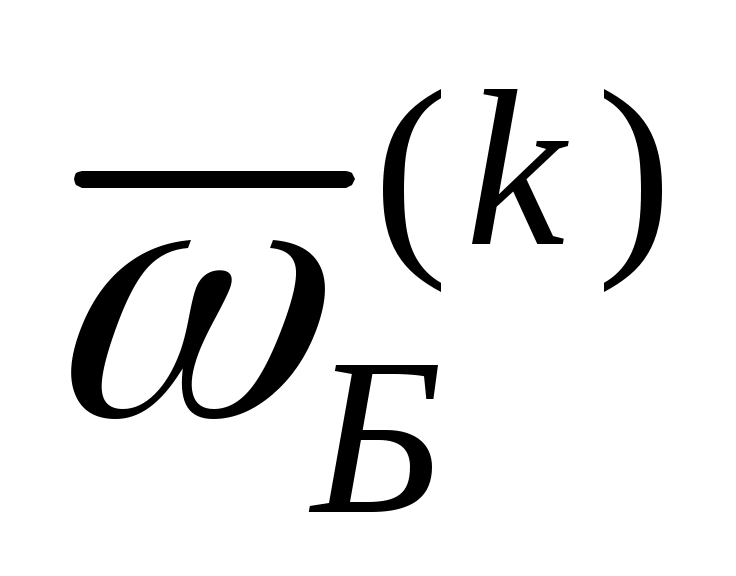 относительно осей нормальной системы может быть вычислен с помощью вектора
относительно осей нормальной системы может быть вычислен с помощью вектора 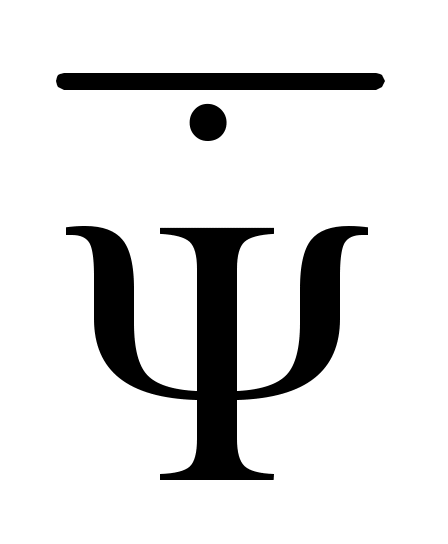 , определяющего поворот на угол
, определяющего поворот на угол  относительно оси OYg нормальной системы, и вектора
относительно оси OYg нормальной системы, и вектора  , определяющего поворот на угол
, определяющего поворот на угол  вокруг оси OZk траекторной системы. Спроецируем векторы
вокруг оси OZk траекторной системы. Спроецируем векторы 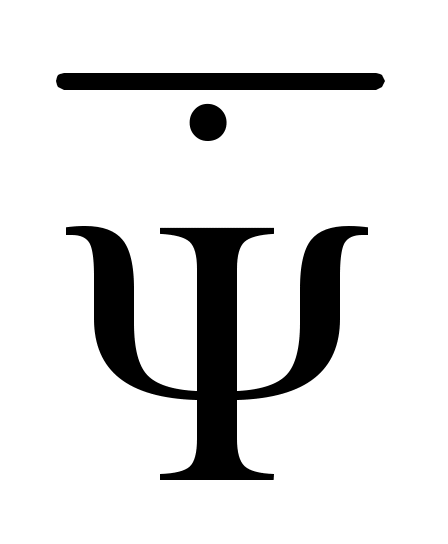 и
и  на оси траекторной системы:
на оси траекторной системы:
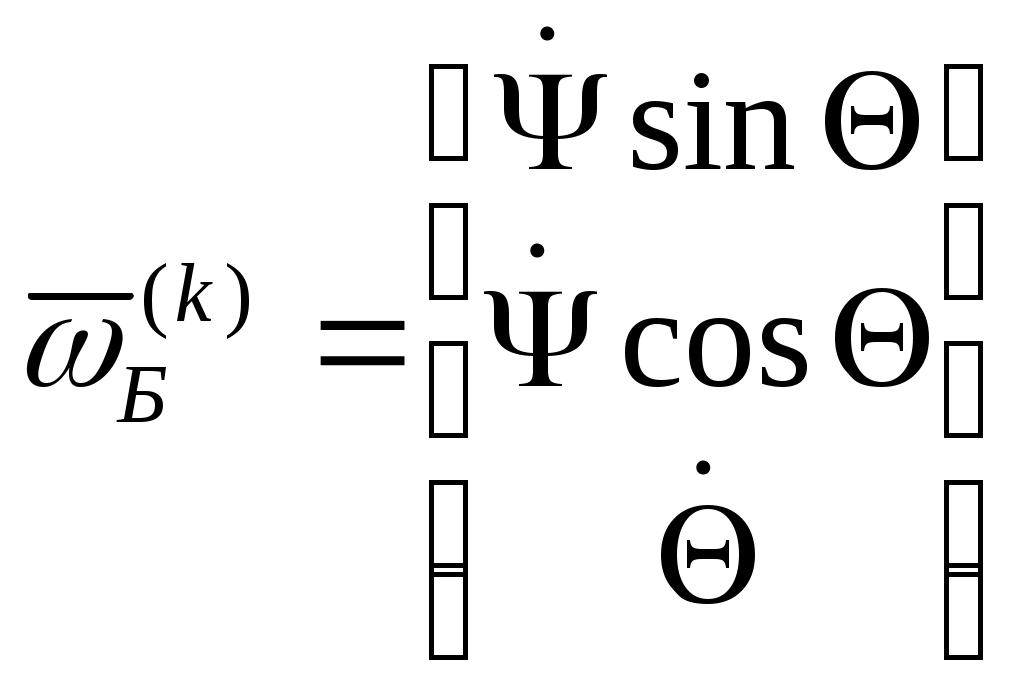
Тогда векторное произведение
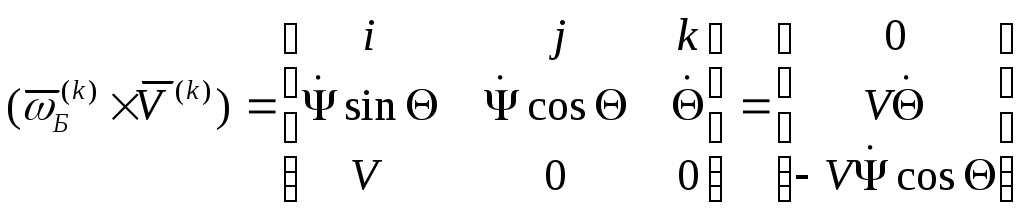
Таким образом, получили уравнения сил в проекциях на оси траекторной системы координат:
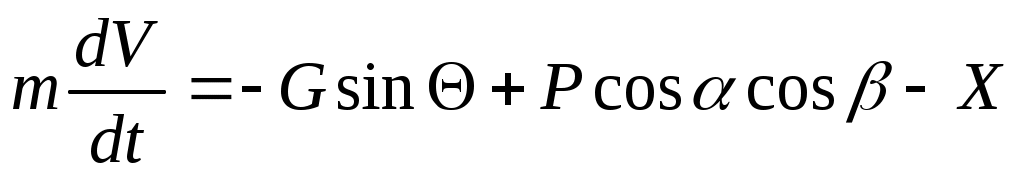 ; (1)
; (1)
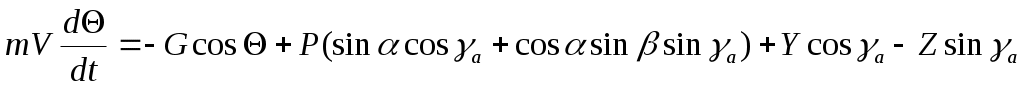 ; (2)
; (2)
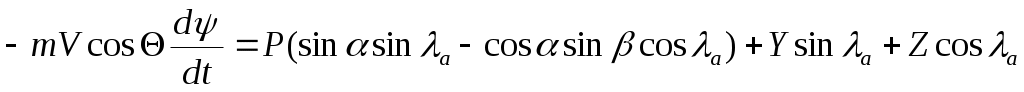 . (3)
. (3)
Уравнение моментов, характеризующее вращение ЛА вокруг центра масс, получим на основании теоремы об изменении кинетического момента:
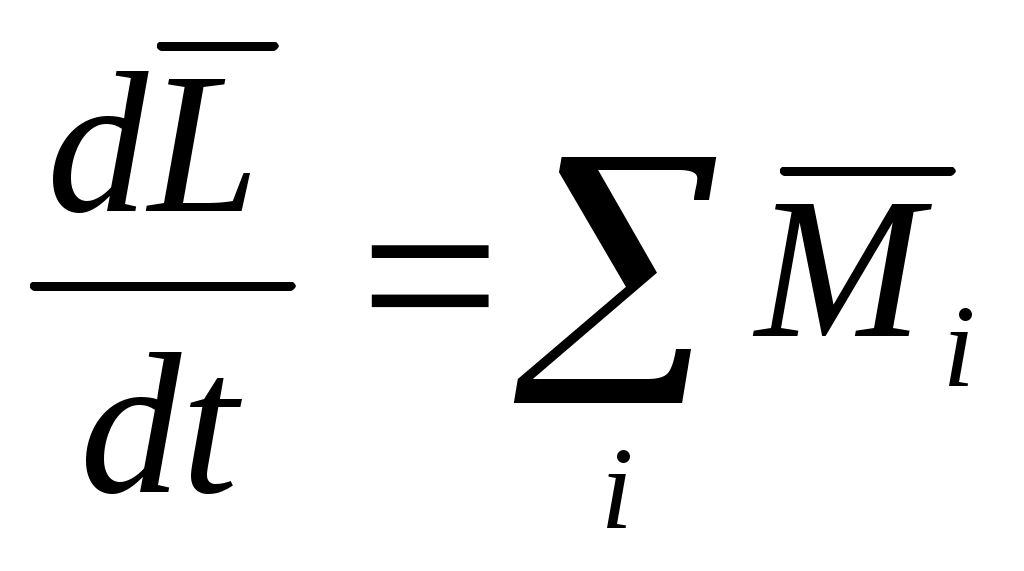 ,
,
где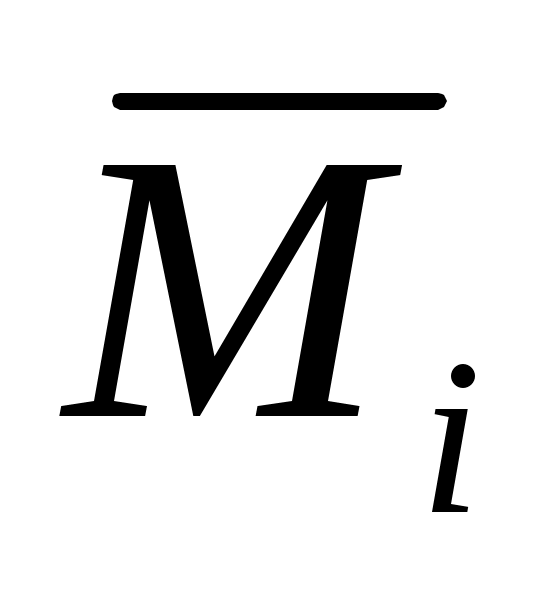 – внешние моменты, действующие на ЛА;
– внешние моменты, действующие на ЛА;
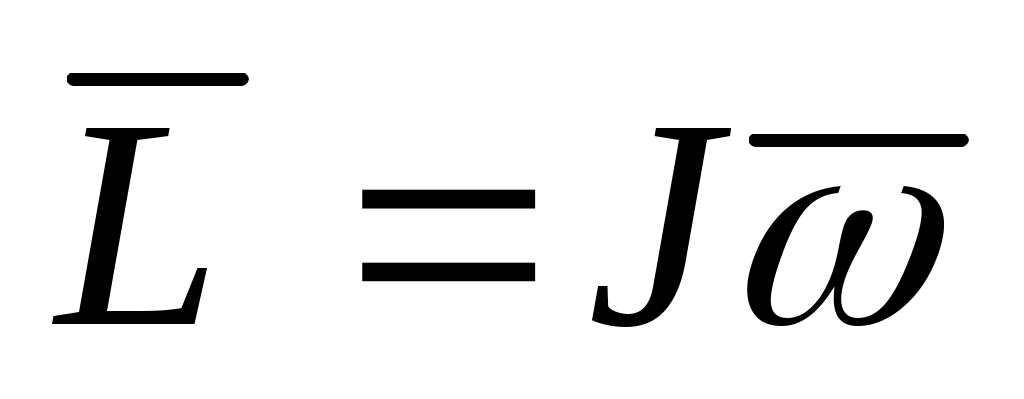 – вектор кинетического момента относительно центра масс;
– вектор кинетического момента относительно центра масс;
Здесь – вектор угловой скорости вращения ЛА относительно центра масс;
– вектор угловой скорости вращения ЛА относительно центра масс;
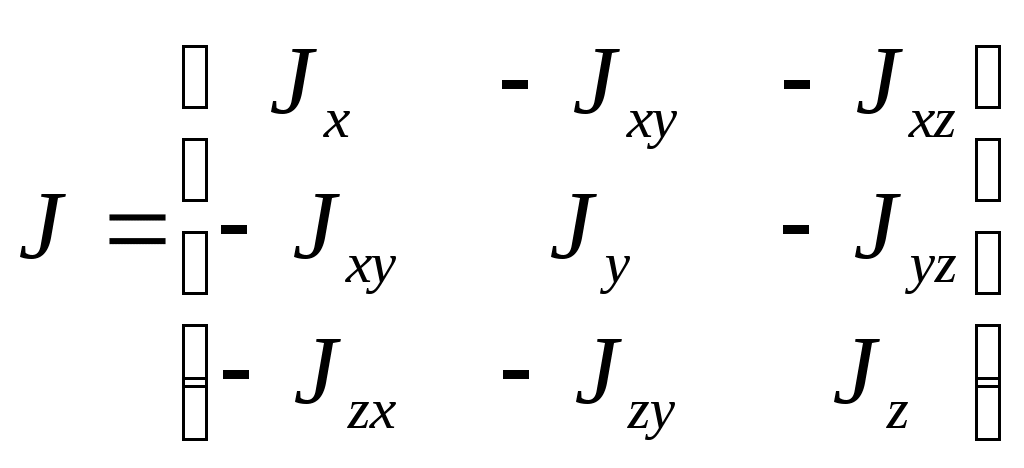 – тензор инерции (здесь главными являются оси связанной системы координат);
– тензор инерции (здесь главными являются оси связанной системы координат);
 – моменты инерции относительно главных осей;
– моменты инерции относительно главных осей;
 – центробежные моменты инерции.
– центробежные моменты инерции.
Для ЛА, имеющих две взаимно перпендикулярные плоскости симметрии,
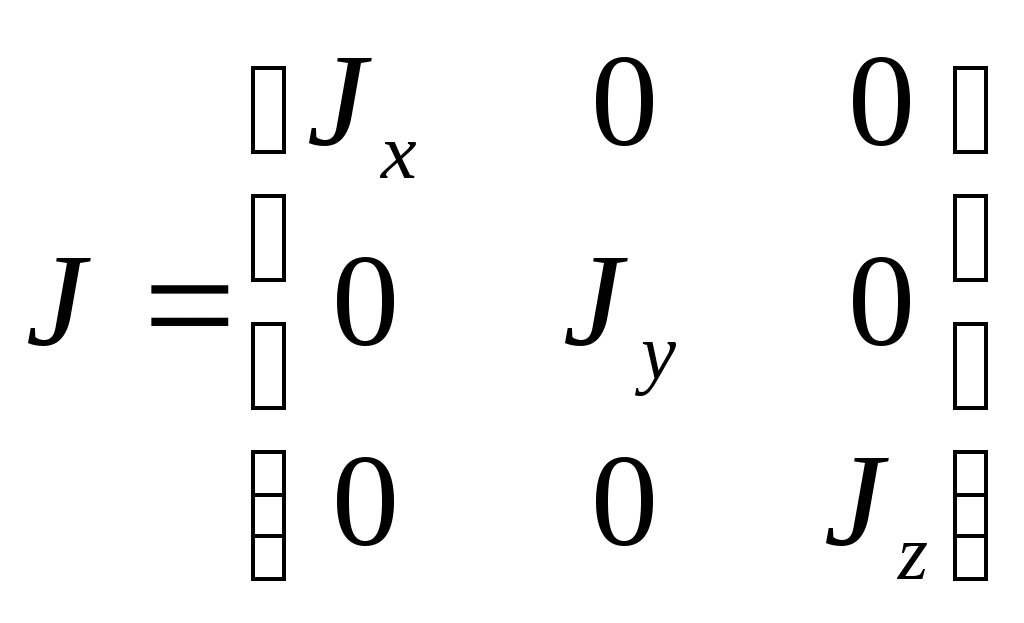 .
.
Для самолетов
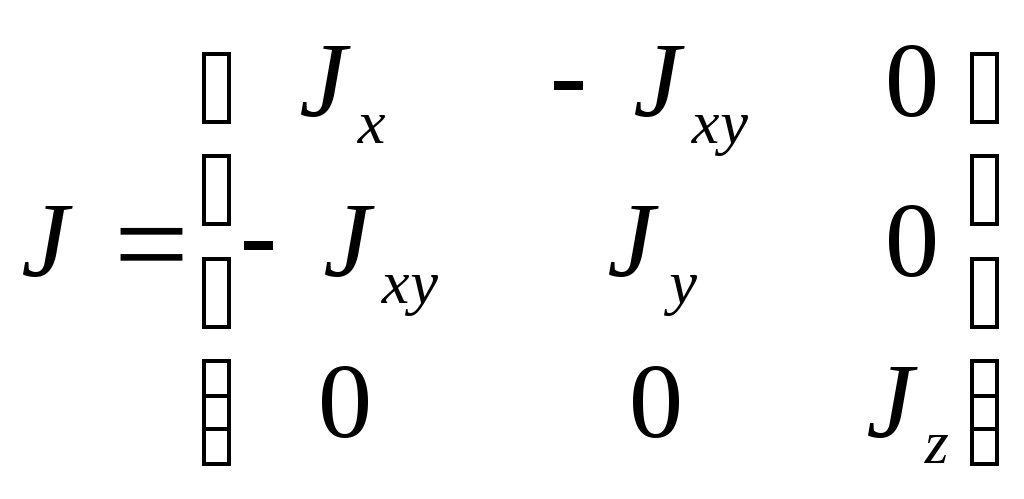 .
.
Уравнение моментов в аэродинамике проецируют на оси связанной системы координат. Положим, что ЛА имеет две плоскости симметрии, т.е.
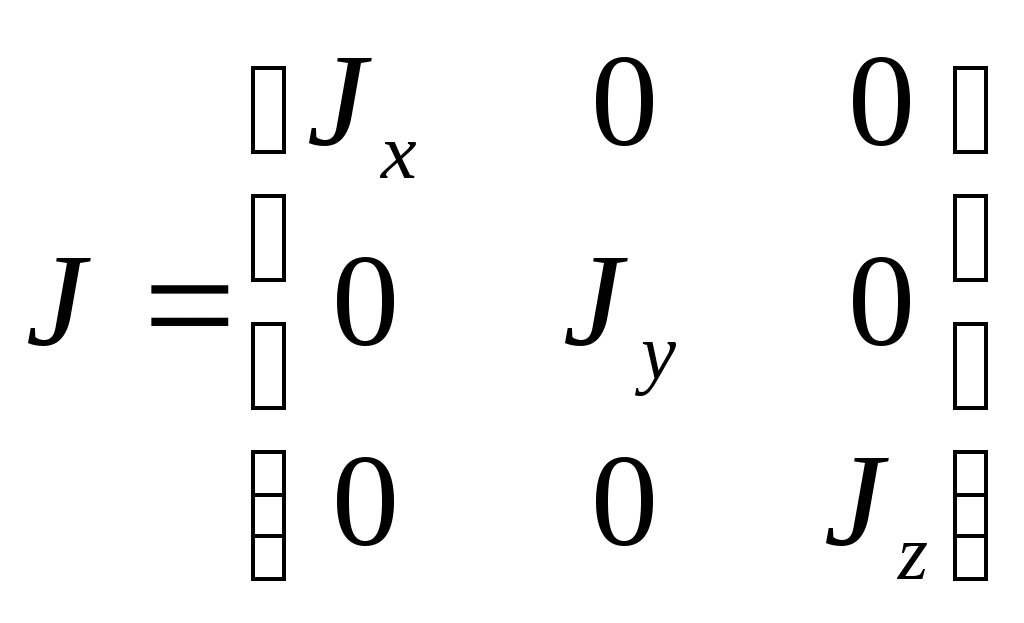 .
.
Запишем вектор угловой скорости в проекциях на оси связанной системы:
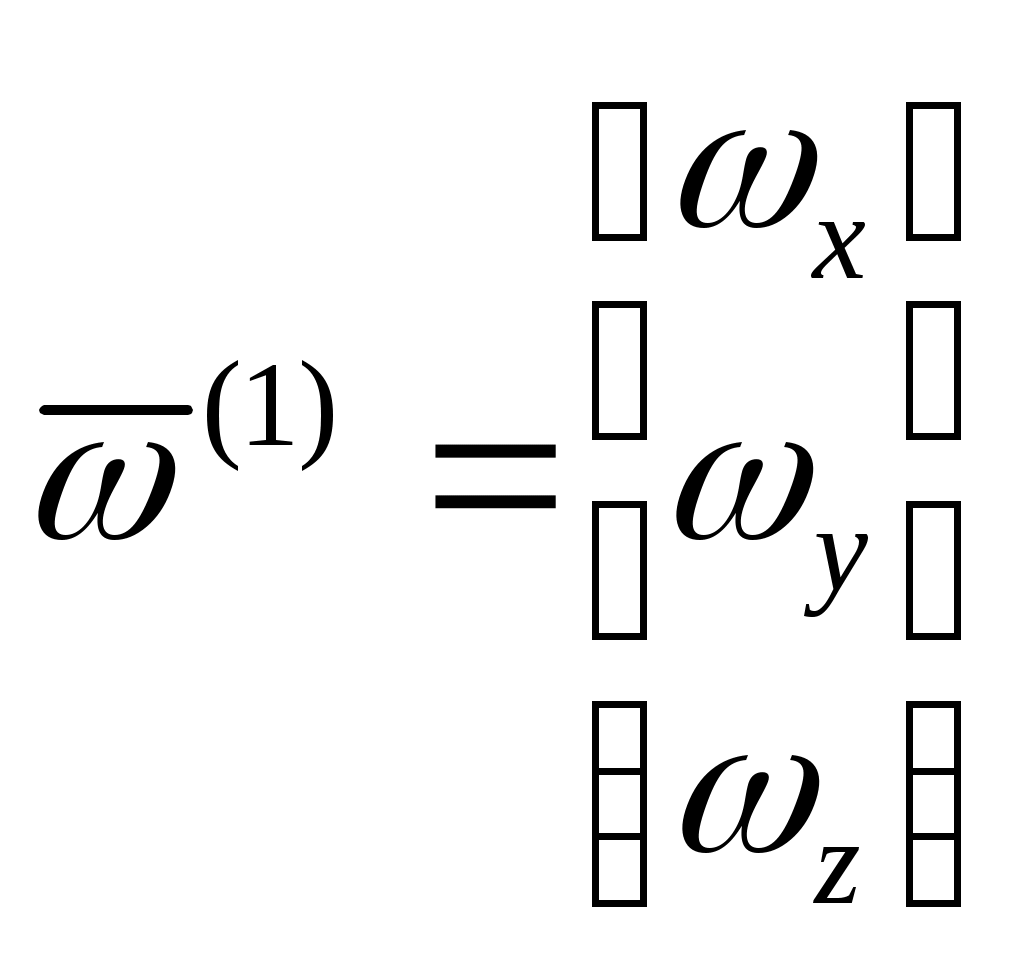 .
.
Тогда
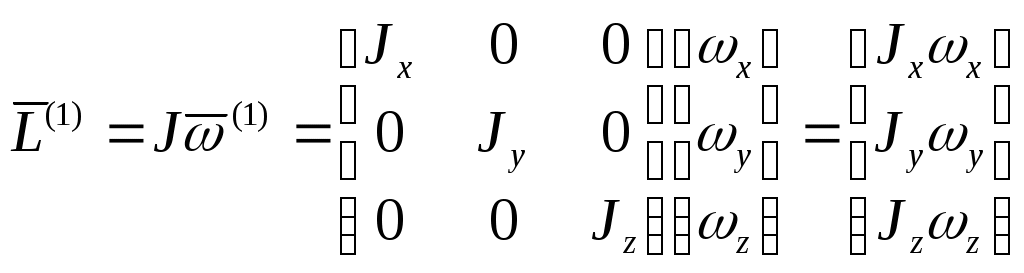
Найдём полную производную
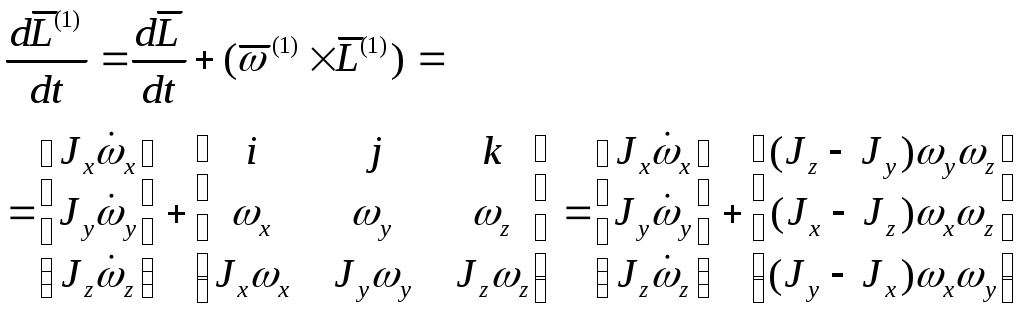
Внешние моменты, действующие на ЛА в проекциях на связанные оси, запишем в следующем виде:
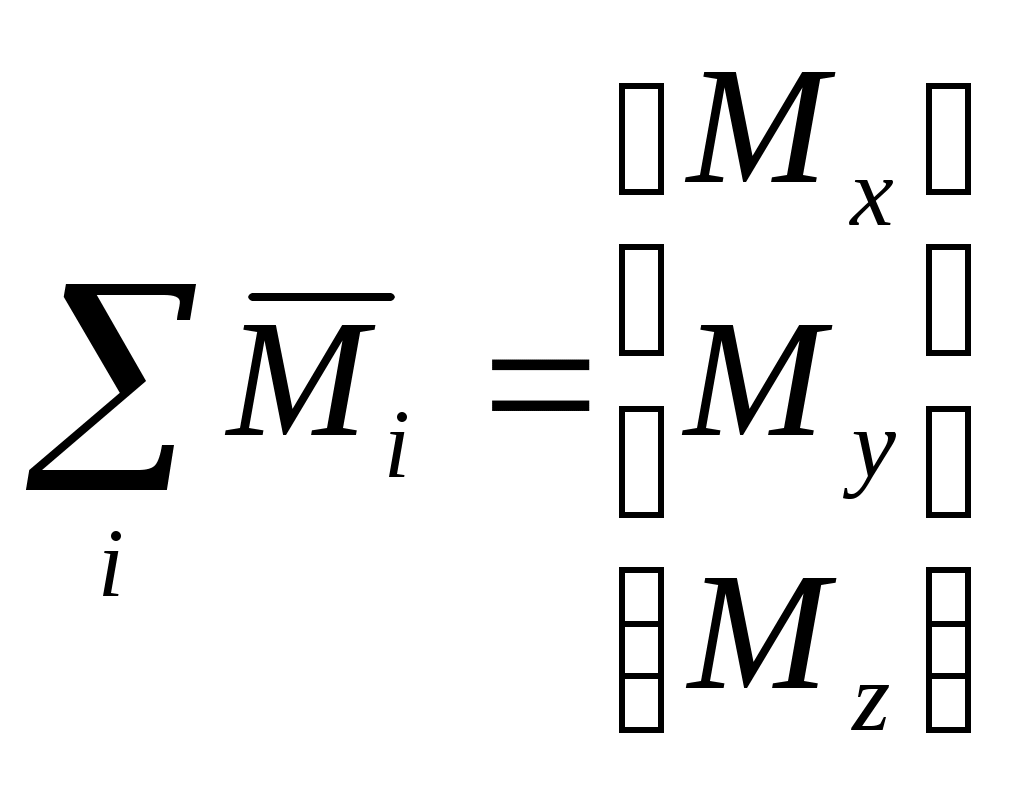
Таким образом, имеем:
 ; (4)
; (4)
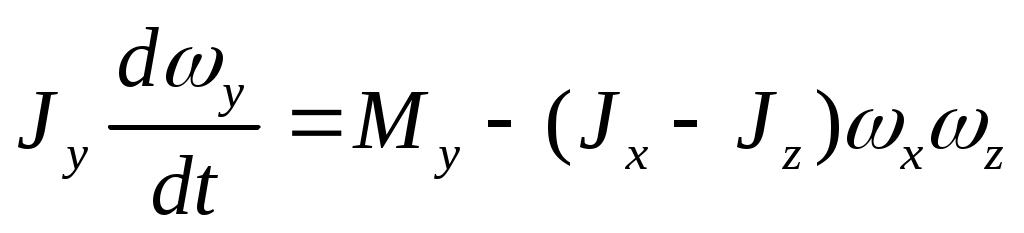 ; (5)
; (5)
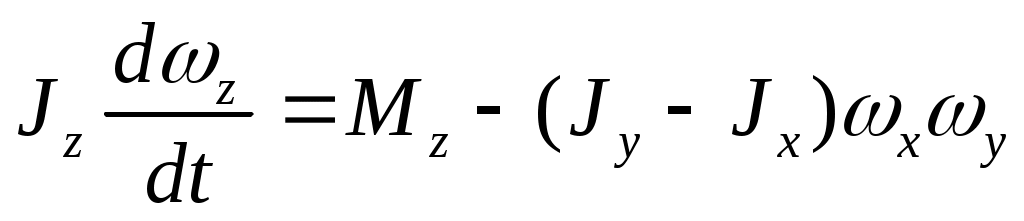 . (6)
. (6)
Для ЛА с двумя плоскостями симметрии, как правило, выполняется соотношение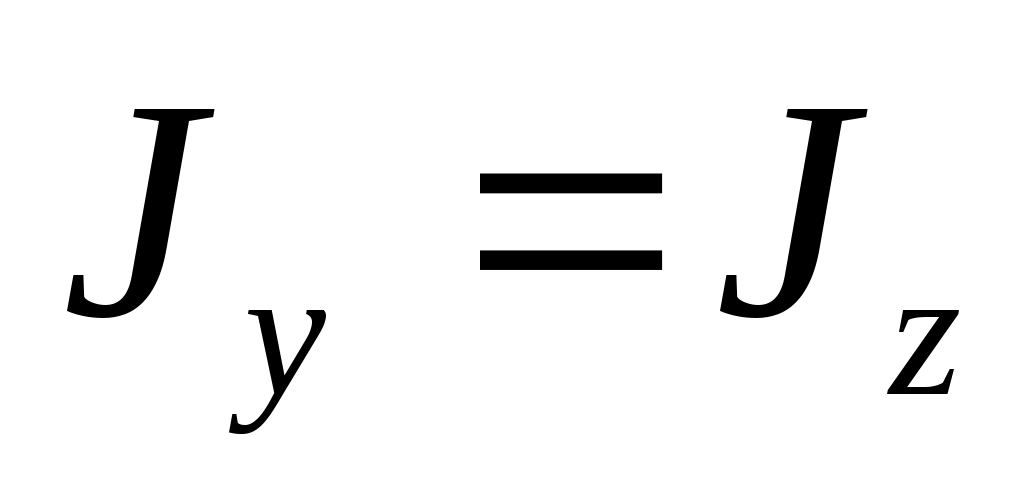 . Тогда первое из уравнений моментов принимает вид:
. Тогда первое из уравнений моментов принимает вид:
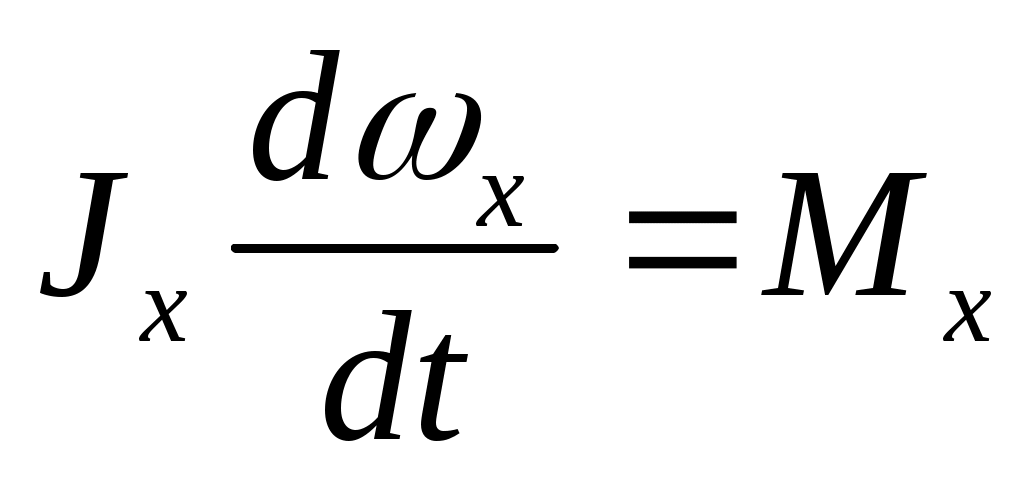 .
.
Теперь необходимо составить кинематические уравнения, характеризующие вращения ЛА относительно осей нормальной системы координат. В уравнениях (4) – (6) заданы проекции угловой скорости относительно связанных осей: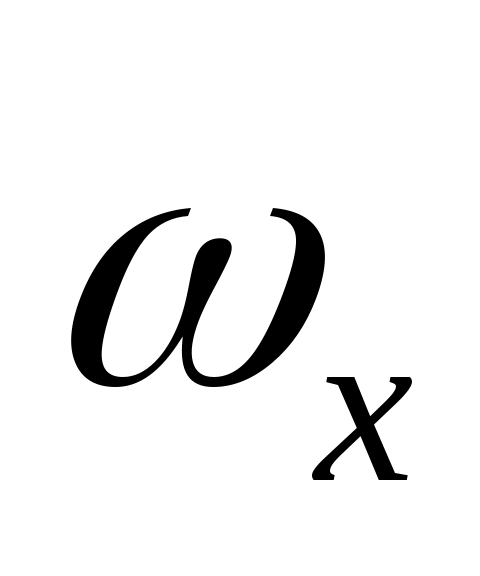 ,
, 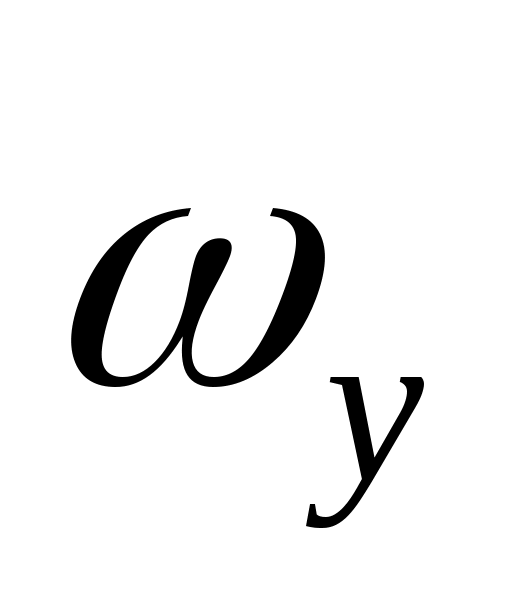 ,
, 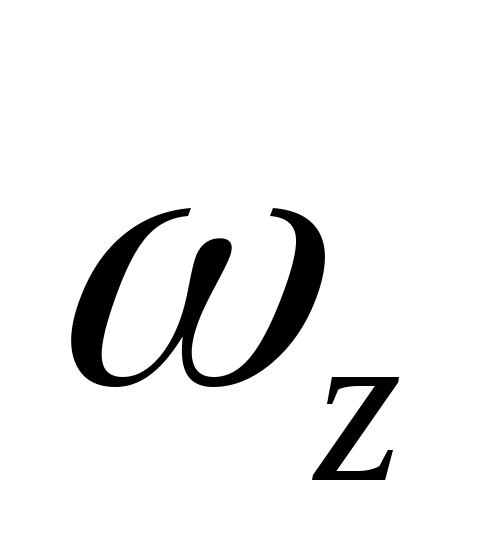 . При переходе из нормальной системы в связанную (рис. 5а) осуществляется вращении ЛА последовательно на угол
. При переходе из нормальной системы в связанную (рис. 5а) осуществляется вращении ЛА последовательно на угол  с угловой скоростью
с угловой скоростью 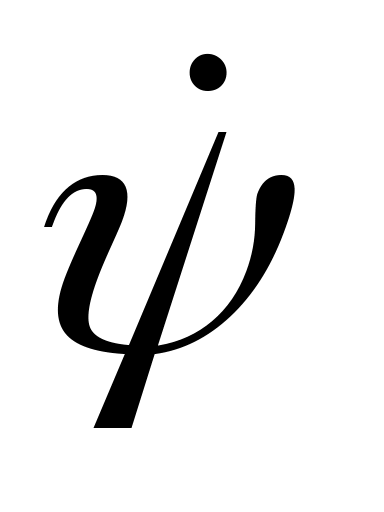 относительно оси OYg, на угол
относительно оси OYg, на угол  с угловой скоростью
с угловой скоростью 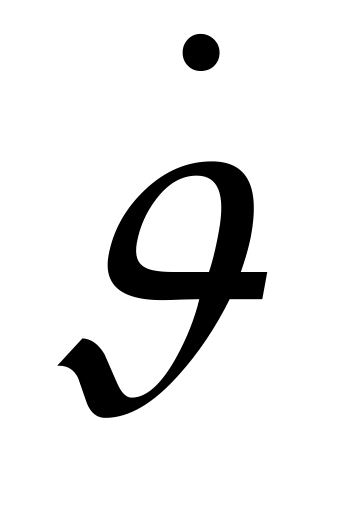 вокруг оси OZ' и на угол
вокруг оси OZ' и на угол  с угловой скоростью
с угловой скоростью 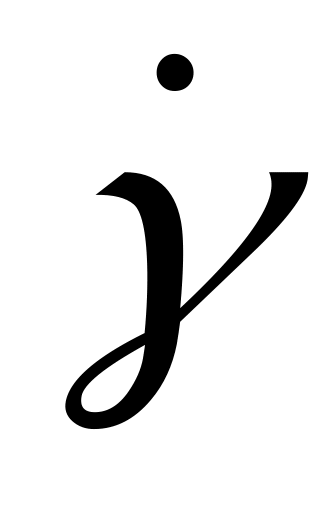 вокруг оси OX. Таким образом, проекции угловой скорости
вокруг оси OX. Таким образом, проекции угловой скорости 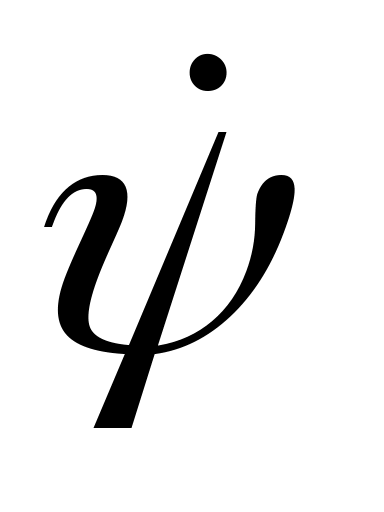 ,
, 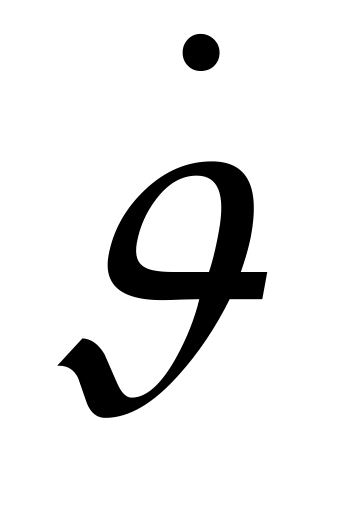 ,
, 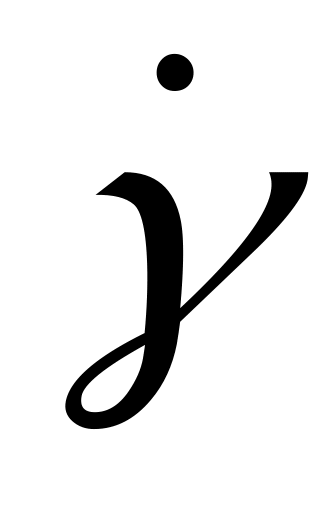 направлены по осям непрямоугольной системы координат OXYgZ’:
направлены по осям непрямоугольной системы координат OXYgZ’:
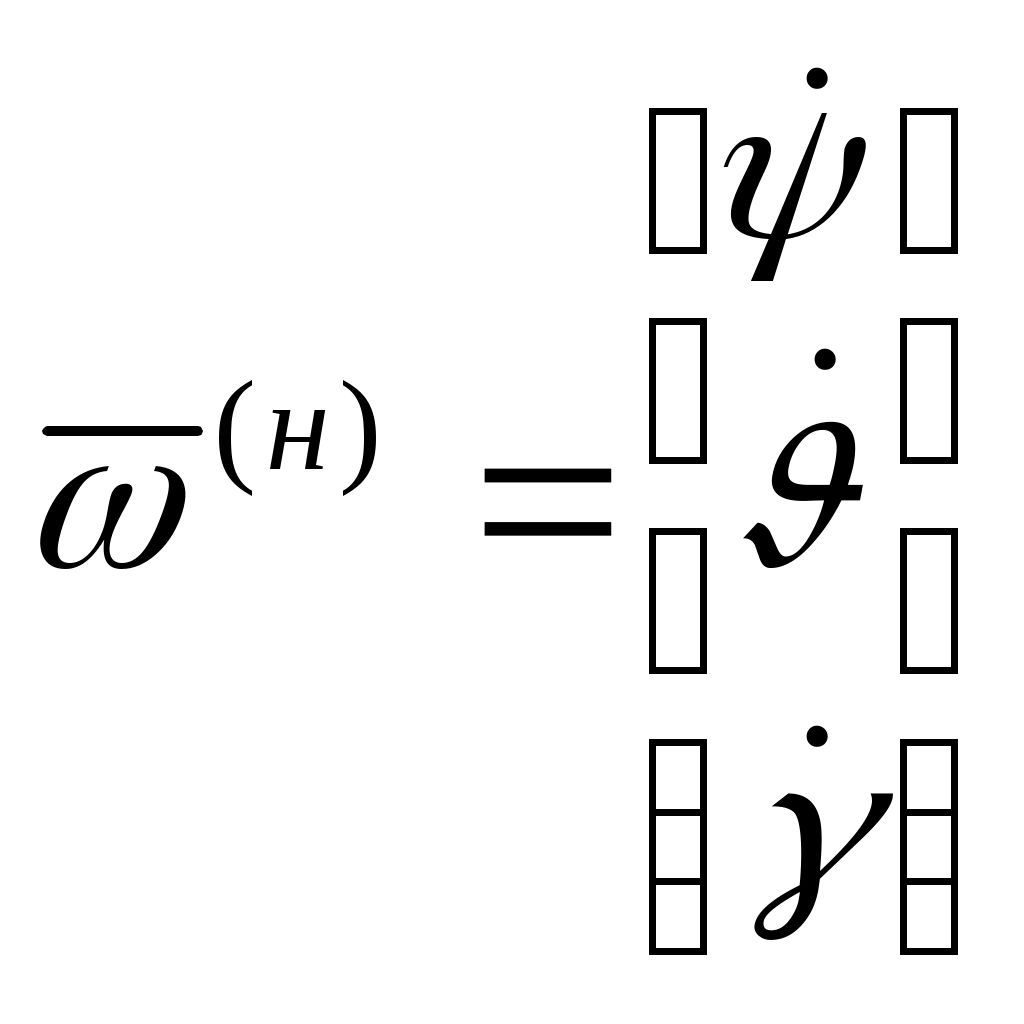
Из рис. 5 видно, что
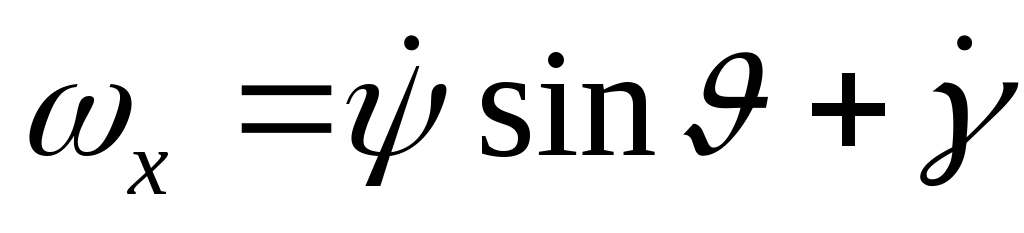 ;
;
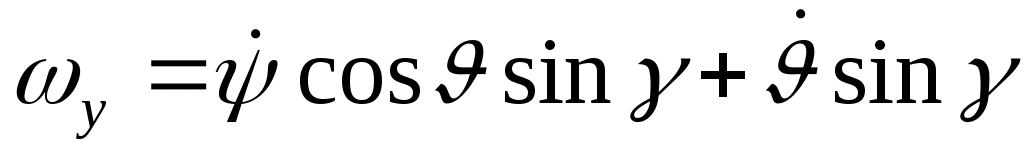 ;
;
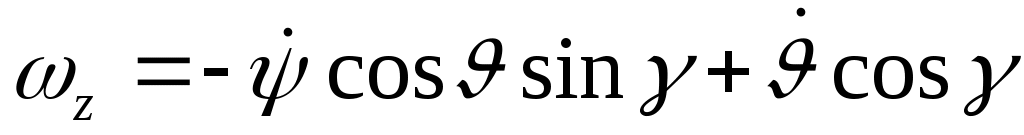 .
.
Отсюда запишем матрицу перехода от непрямоугольной системы к связанной:
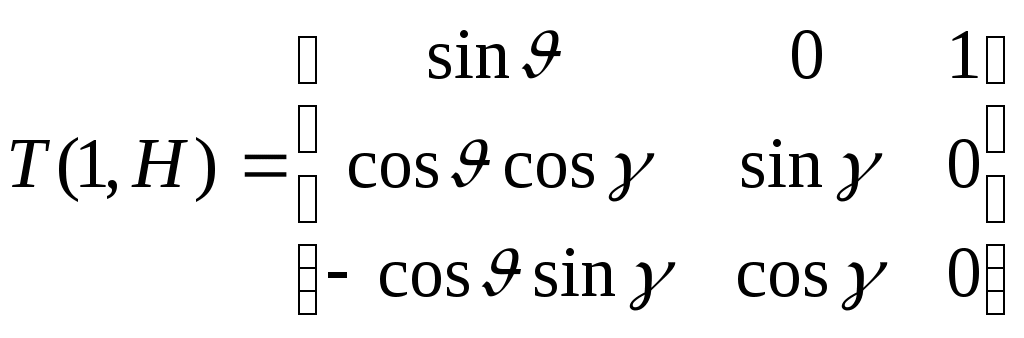
Обычно требуется провести обратное преобразование T(H,1), которое находят по обычным правилам вычисления обратных матриц:
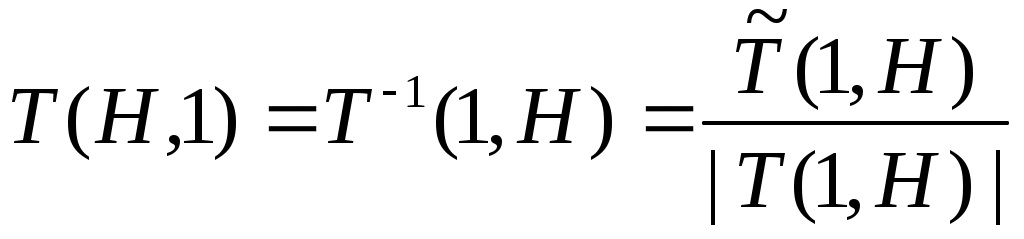 .
.
Нетрудно видеть, что определитель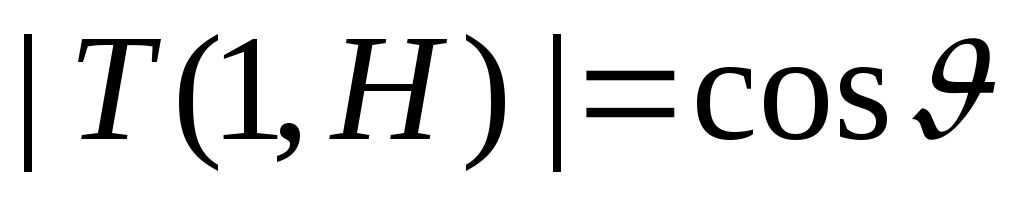 .
.
Запишем взаимную матрицу
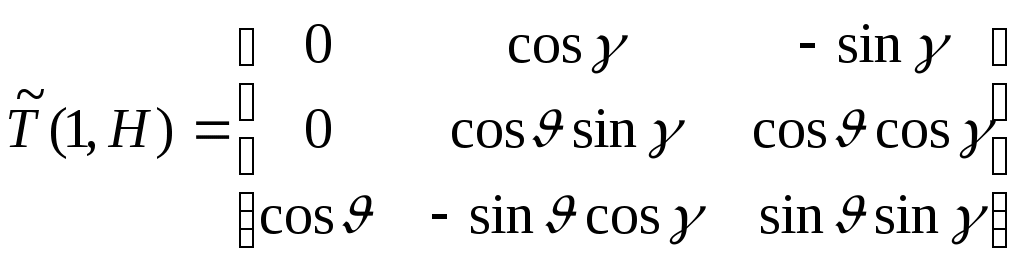 .
.
Таким образом, связь между проекциями угловой скорости в разных базисах выражается следующими уравнениями:
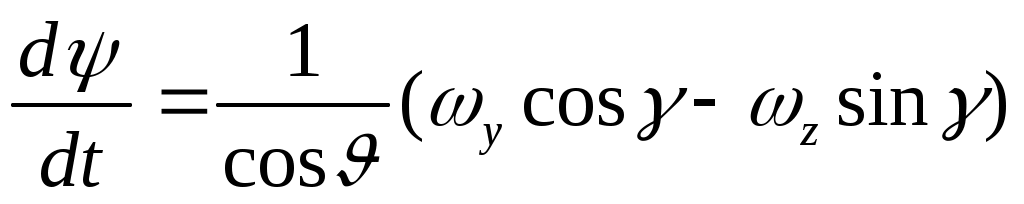 ; (7)
; (7)
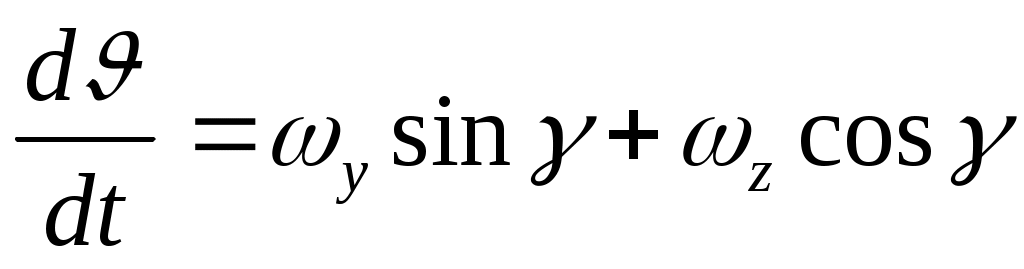 ; (8)
; (8)
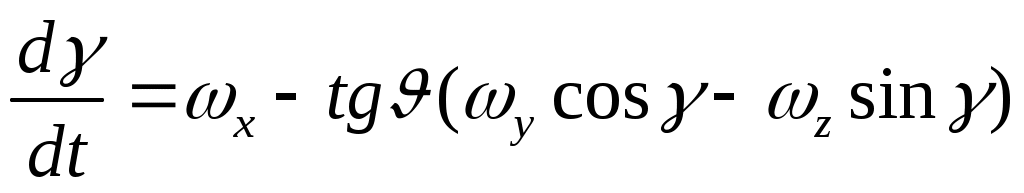 . (9)
. (9)
Поскольку уравнения движения центра масс (1), (2), (3) записаны в траекторных осях, уравнения вращательного движения вокруг центра масс (4) – (9) – в связанных осях, а аэродинамические силы и моменты в правых частях уравнений (1) – (6) зависят от углов атаки и скольжения
и скольжения  между скоростными и связанными осями, то возникает необходимость в добавлении к записанным уравнениям геометрических соотношений между углами
между скоростными и связанными осями, то возникает необходимость в добавлении к записанным уравнениям геометрических соотношений между углами  ,
,  ,
,  и углами
и углами  ,
,  ,
,  ,
, 
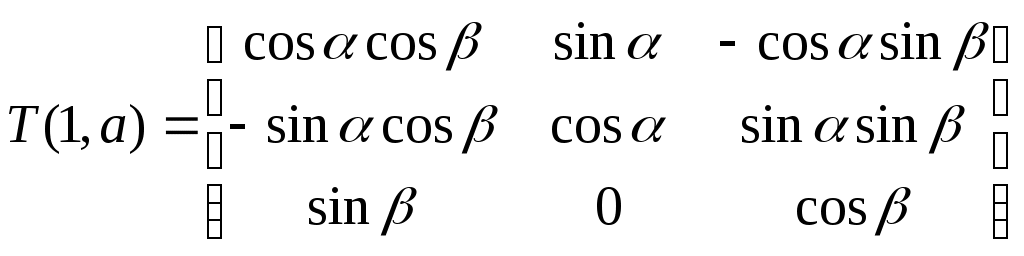
Подробная классификация систем координат и матриц перехода из одной системы в другую дана в [2].
В рекомендуемой литературе [1]-[5] все определения и обозначения даны в соответствии с ГОСТ 1075-41. Для облегчения перехода от системы обозначений ГОСТ 1075-41 к принятой в настоящее время системе ГОСТ 20058-74 следует пользоваться.
§ 3. Дифференциальные уравнения движения летательного аппарата
При выводе уравнений движения ЛА делает следующие допущения:
1. ЛА рассматривается как абсолютно твёрдое тело переменной массы, имеющие 6 степеней свободы.
2. Моменты инерции ЛА постоянны.
3. ЛА имеет вертикальную плоскость симметрии.
3. Не учитываются влияние ветра, сферичность и вращение земли.
Уравнения движения центра масс ЛА получим основании закона изменения количества движения центра масс:
Здесь
Fi – внешние силы, действующие на ЛА.
Обычно уравнения сил проецируют на оси траекторной системы координат, так как в это случае Vx=V, Vy=Vz=0 и уравнения получают в достаточно простом виде.
Выразим координаты всех сил в базисе траекторной системы.
Прежде всего рассмотрим эти силы.
1. Сила тяжести. Поскольку эта сила направлена по местной вертикали, её обычно задают в базисе нормальной системы координат:
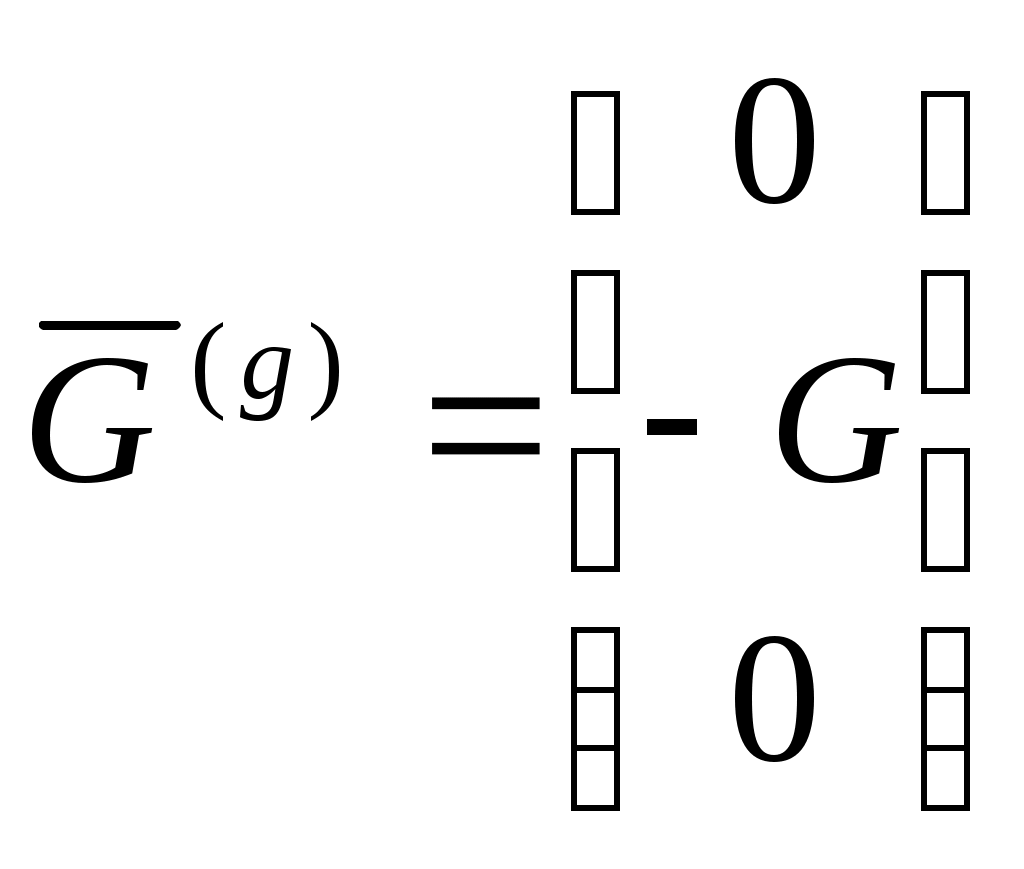
2. Сила тяги двигателя приложена в центре масс двигателя и направлена по оси OX связанной системы. Она задается в базисе связанной системы координат:
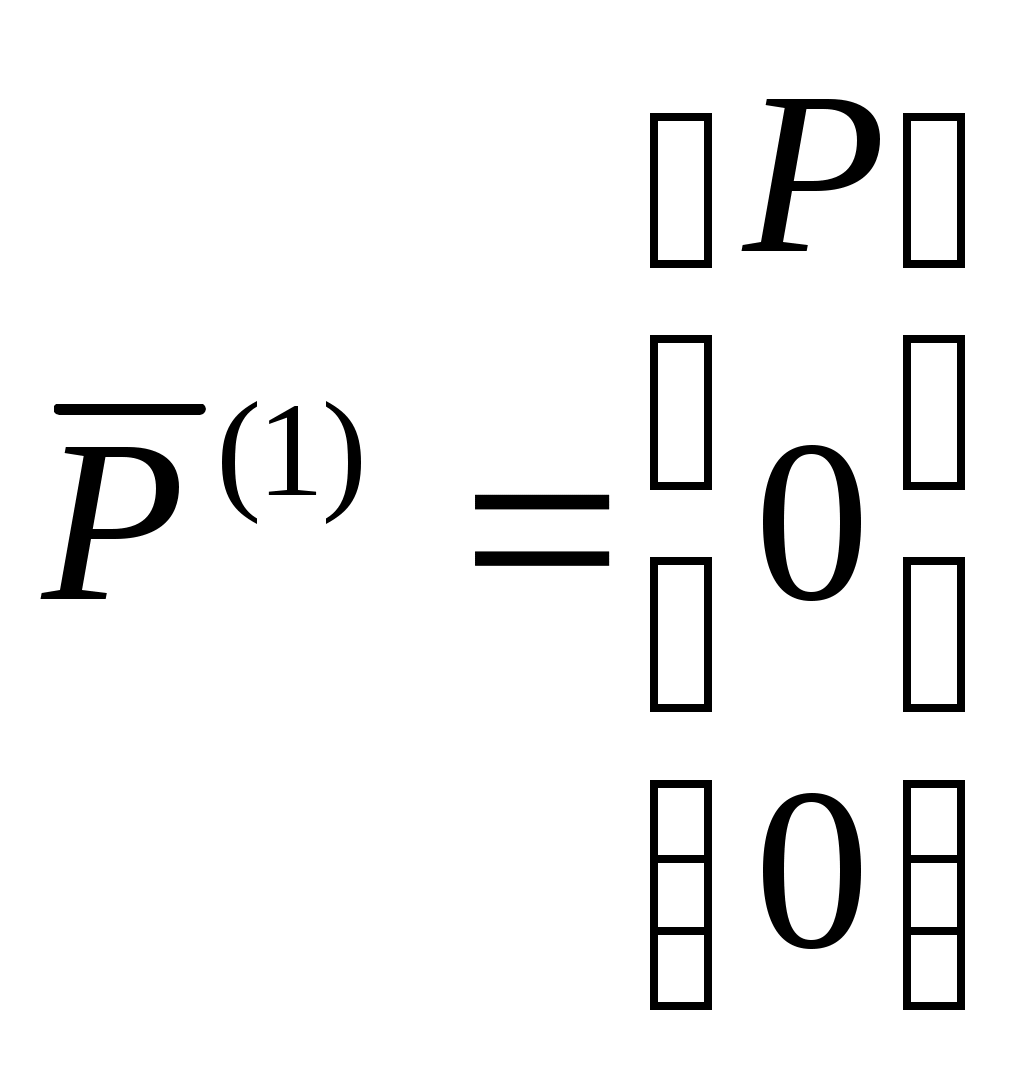
3. Равнодействующая аэродинамических сил обычно записывается в базисе скоростной системы:
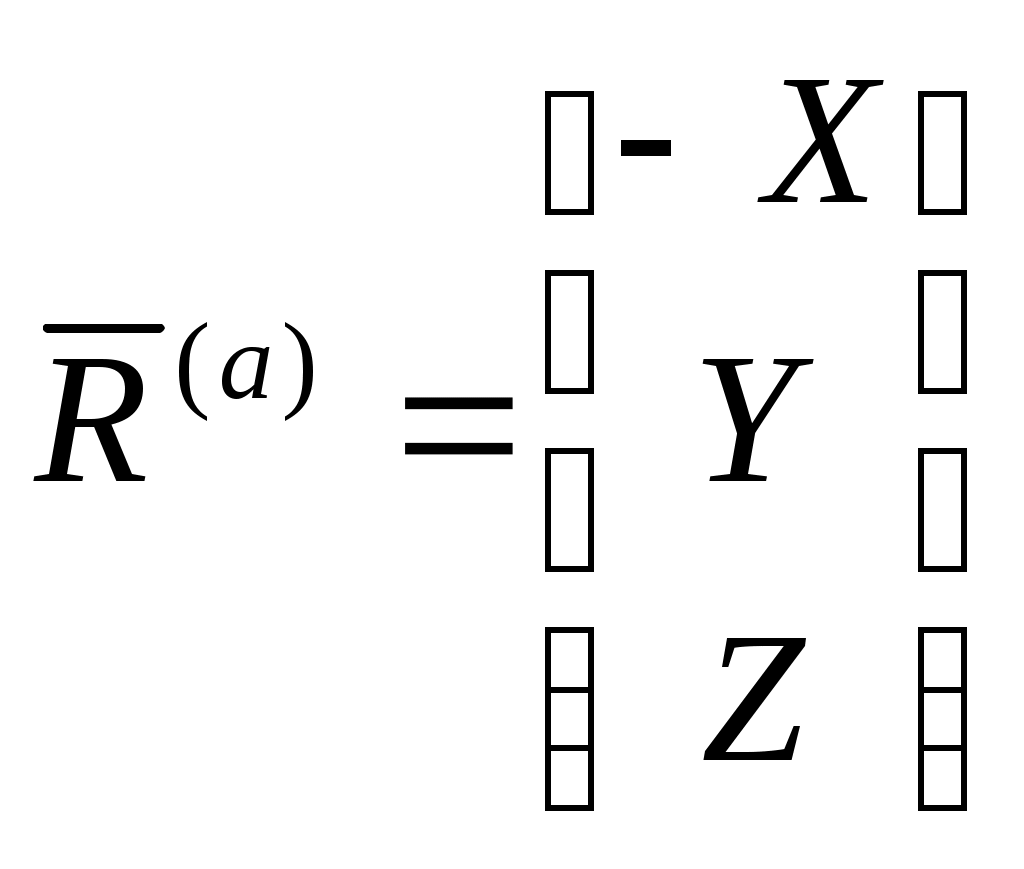
где X – сила лобового сопротивления;
Y – подъемная сила;
Z – боковая сила.
Запишем эти силы в проекциях на оси траекторной системы:
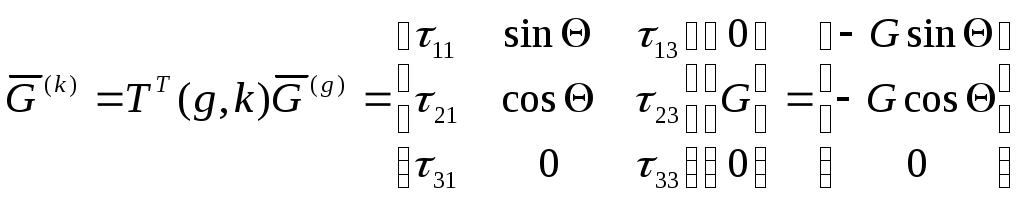
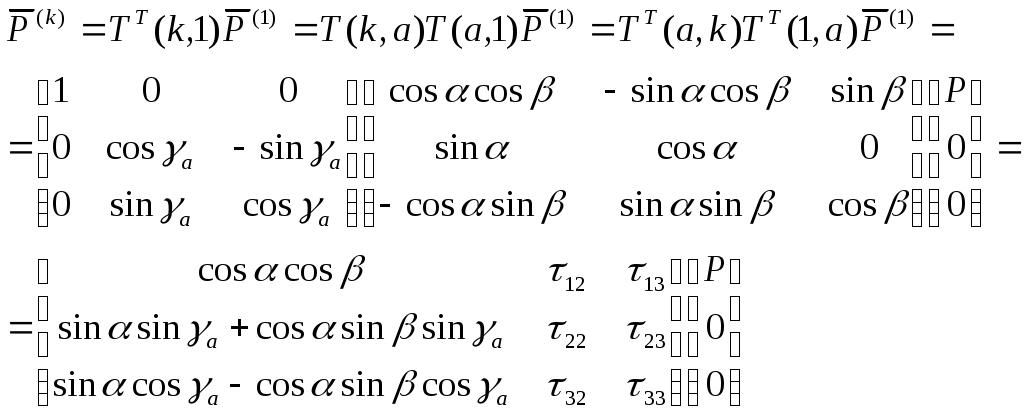
Окончательно
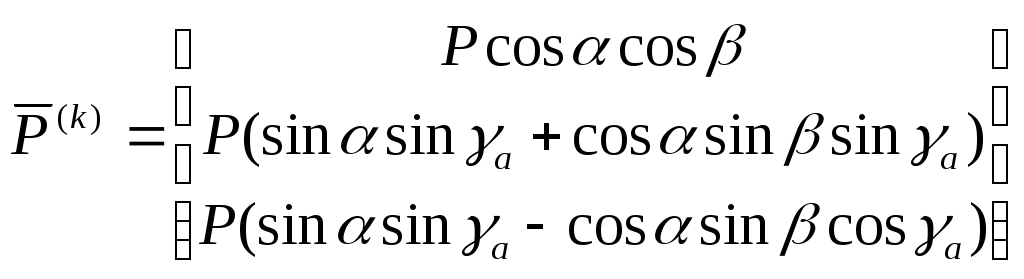
Аэродинамические силы выразятся так:
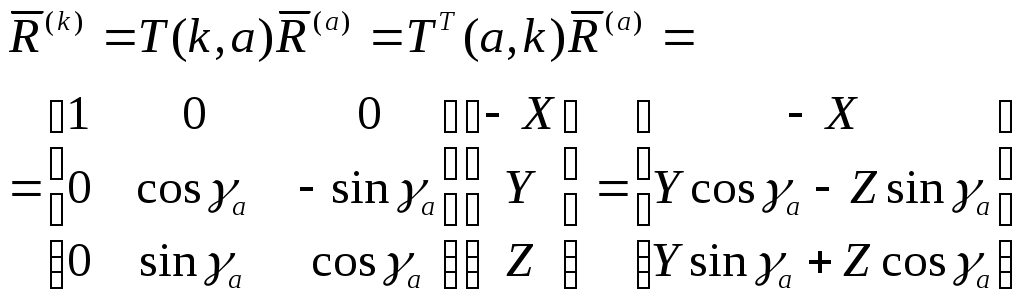
Поскольку проекции вектора скорости в скоростной и траекторной системах координат совпадают, то запишем левую часть уравнения сил в базисе траекторной системы:
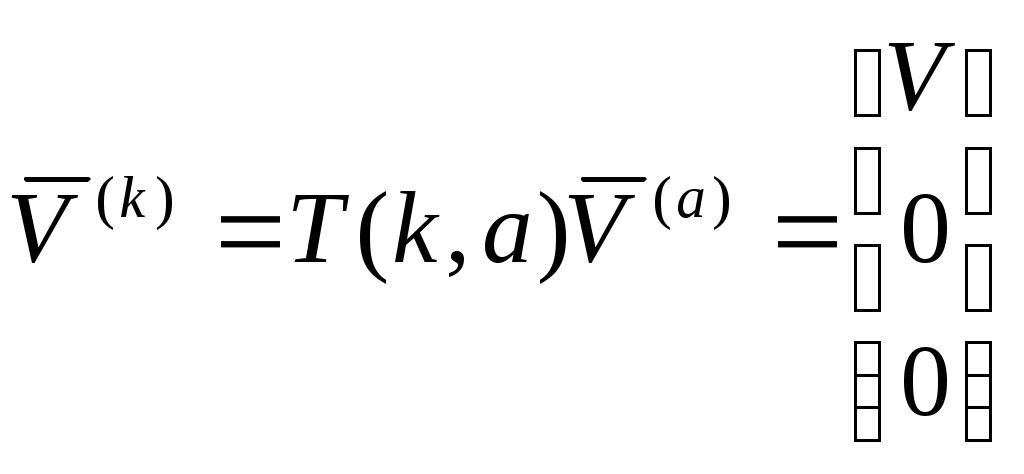
Дифференцируем
где
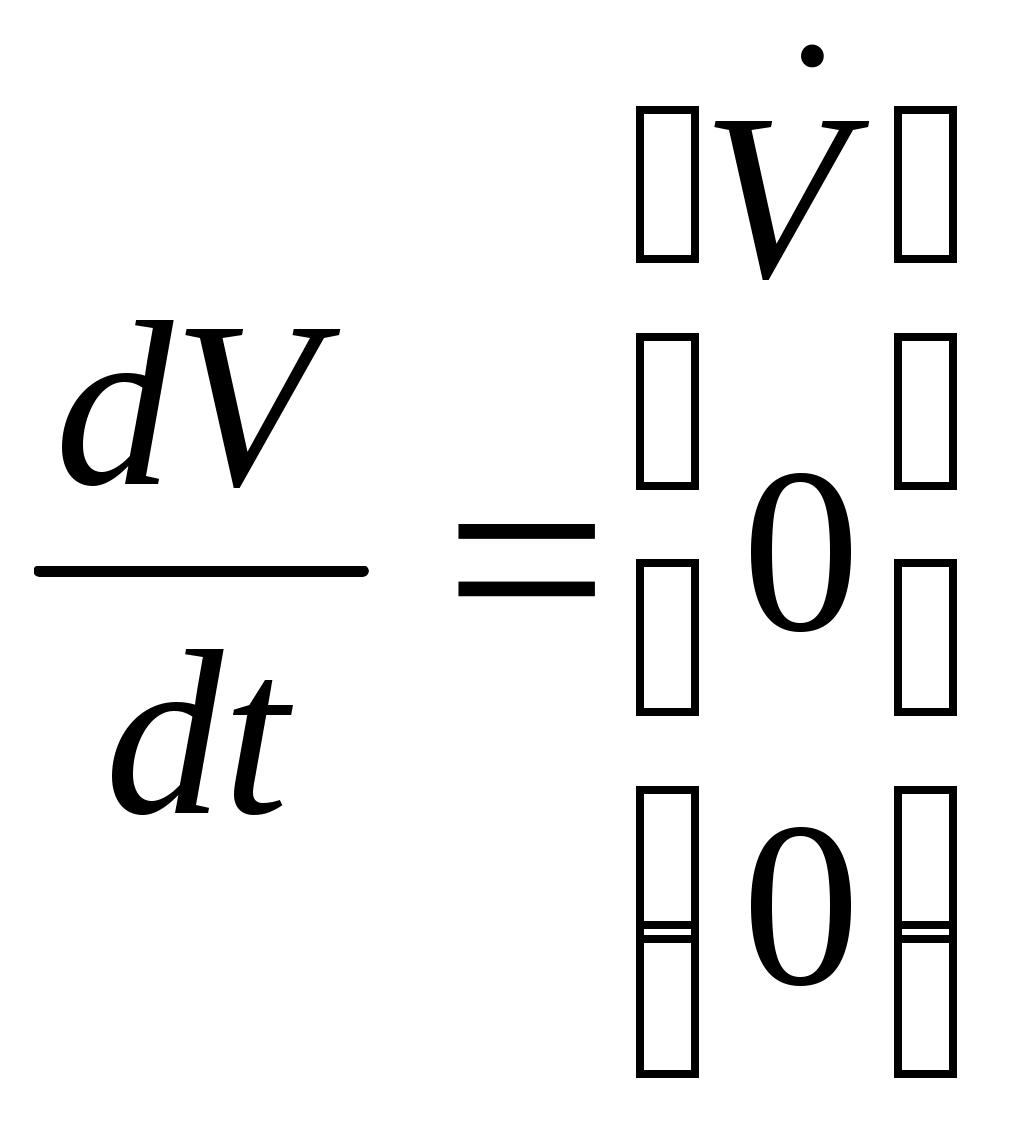 – локальная производная по времени, взятая в предположении неподвижого базиса;
– локальная производная по времени, взятая в предположении неподвижого базиса; 
Рис. 8. Вращение базиса траекторной системы координат в нормальной.
Обратимся к рис. 8. Нетрудно видеть, что вектор угловой скорости траекторной системы координат
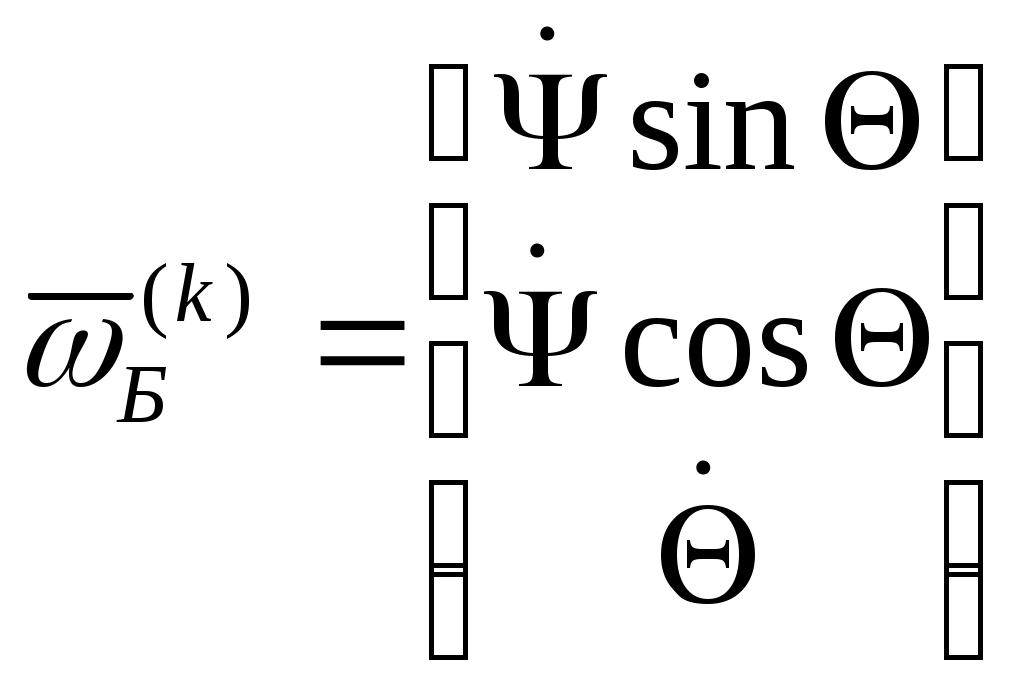
Тогда векторное произведение
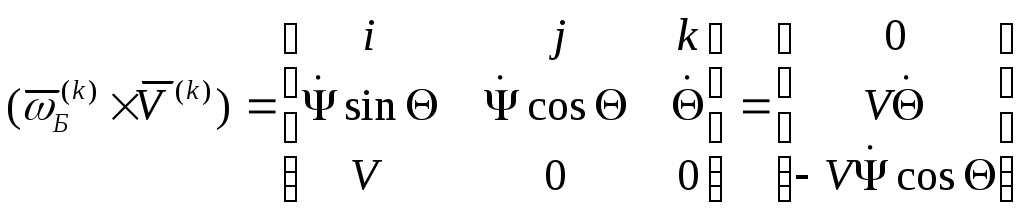
Таким образом, получили уравнения сил в проекциях на оси траекторной системы координат:
Уравнение моментов, характеризующее вращение ЛА вокруг центра масс, получим на основании теоремы об изменении кинетического момента:
где
Здесь
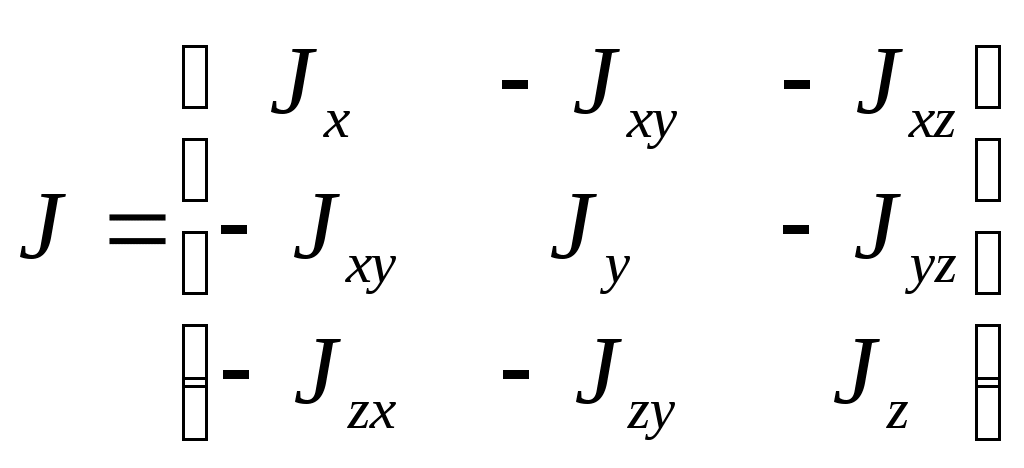 – тензор инерции (здесь главными являются оси связанной системы координат);
– тензор инерции (здесь главными являются оси связанной системы координат);Для ЛА, имеющих две взаимно перпендикулярные плоскости симметрии,
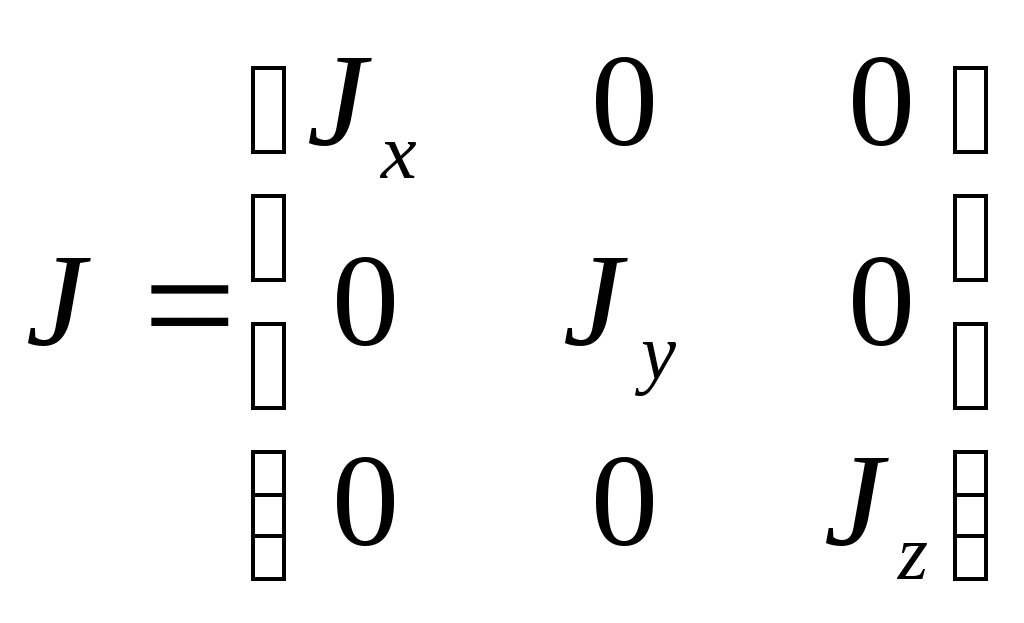 .
.Для самолетов
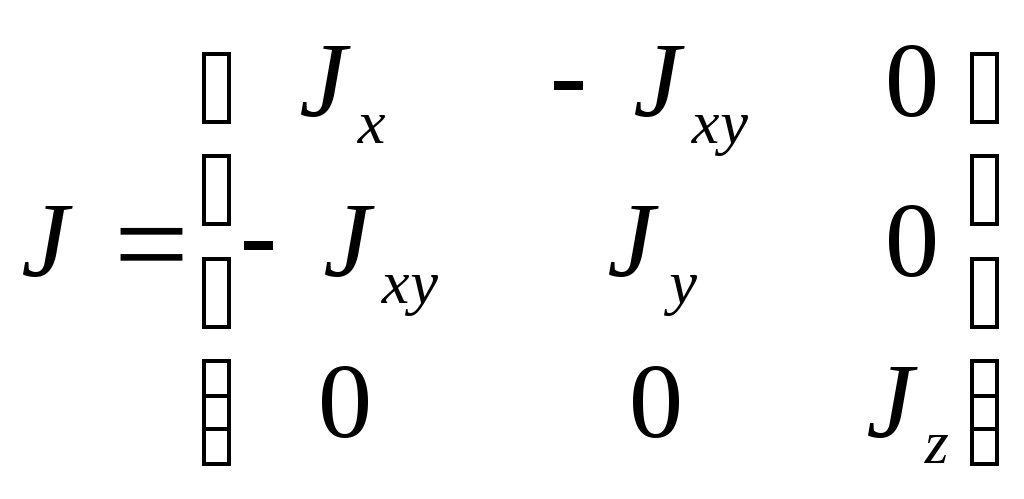 .
.Уравнение моментов в аэродинамике проецируют на оси связанной системы координат. Положим, что ЛА имеет две плоскости симметрии, т.е.
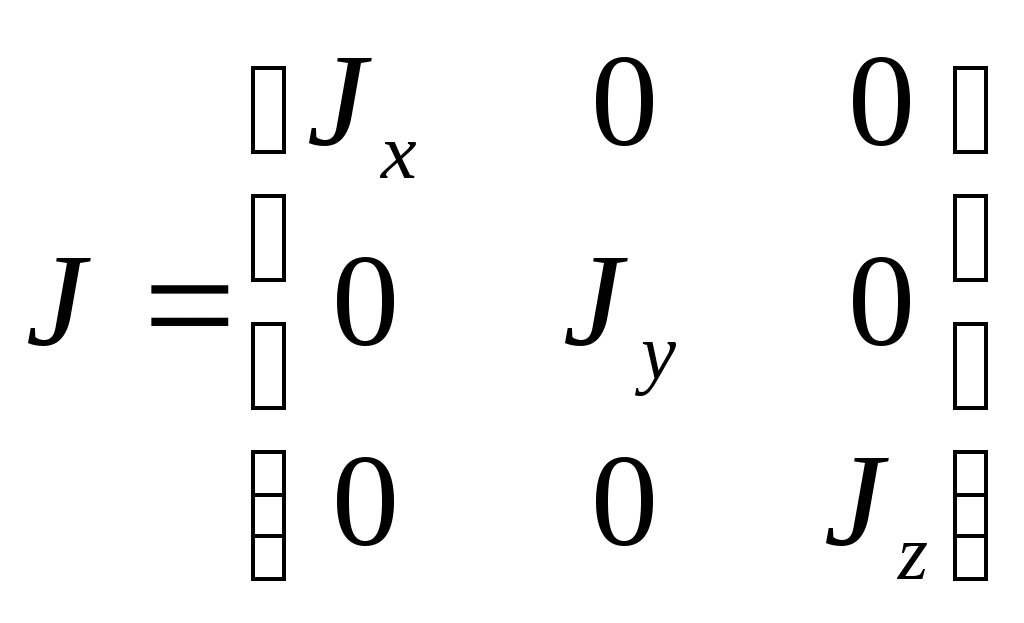 .
.Запишем вектор угловой скорости в проекциях на оси связанной системы:
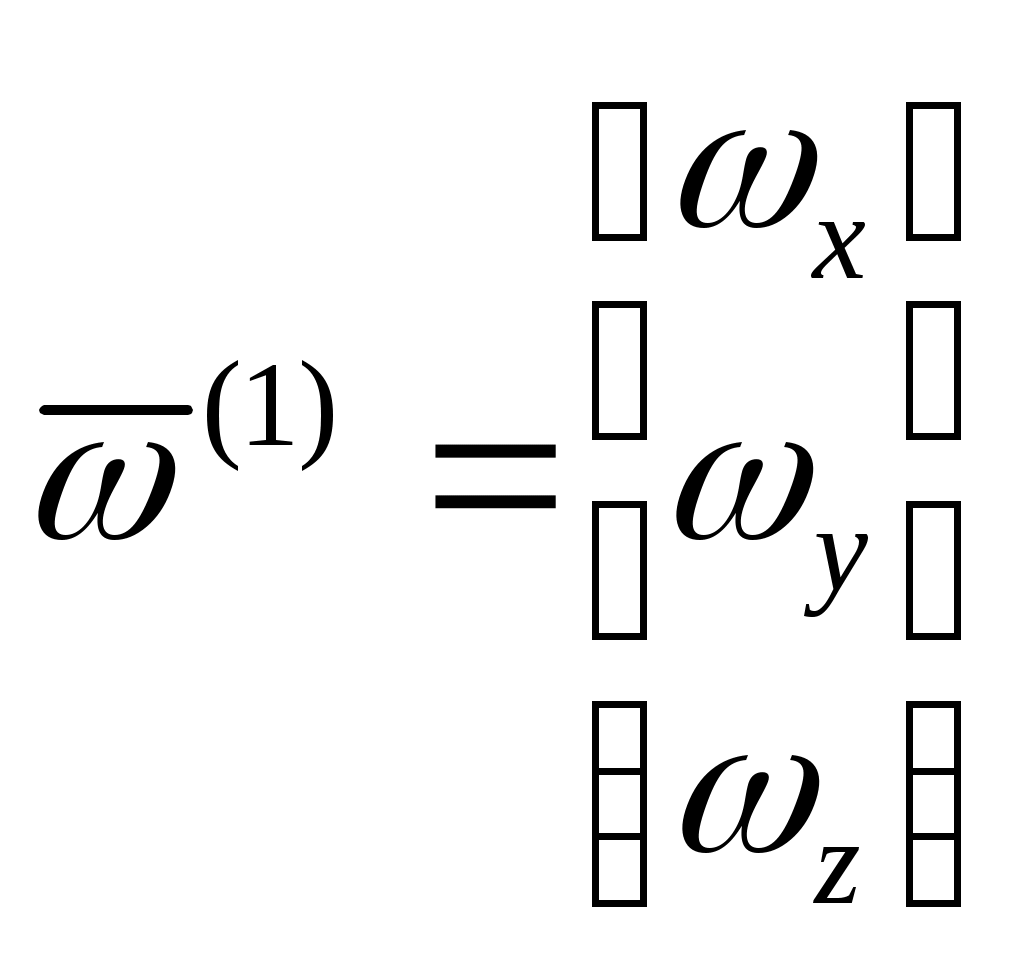 .
.Тогда
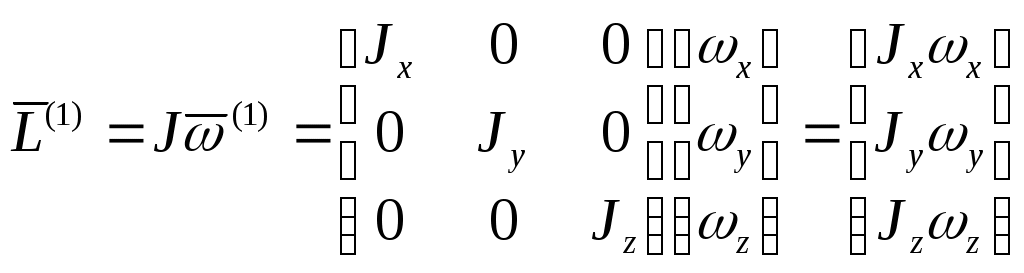
Найдём полную производную
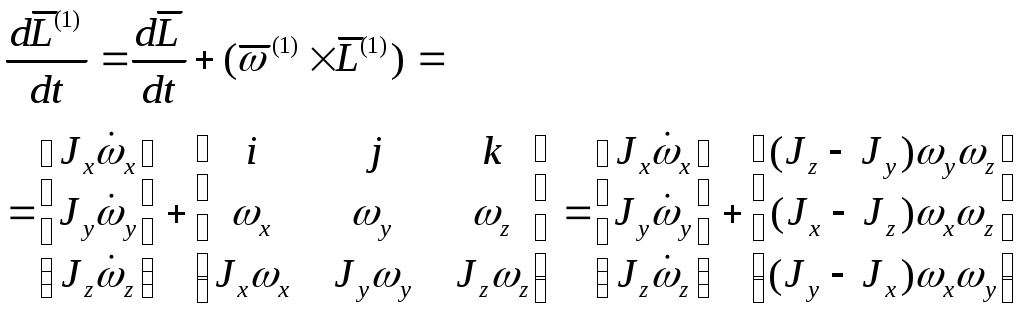
Внешние моменты, действующие на ЛА в проекциях на связанные оси, запишем в следующем виде:
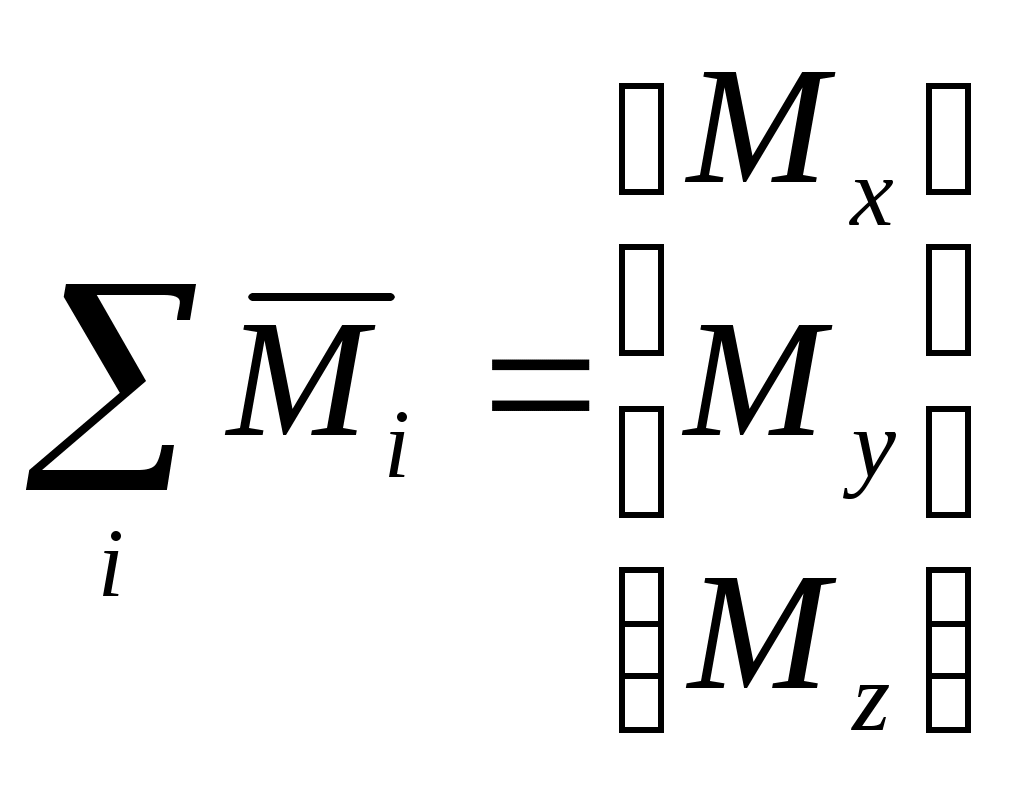
Таким образом, имеем:
Для ЛА с двумя плоскостями симметрии, как правило, выполняется соотношение
Теперь необходимо составить кинематические уравнения, характеризующие вращения ЛА относительно осей нормальной системы координат. В уравнениях (4) – (6) заданы проекции угловой скорости относительно связанных осей:
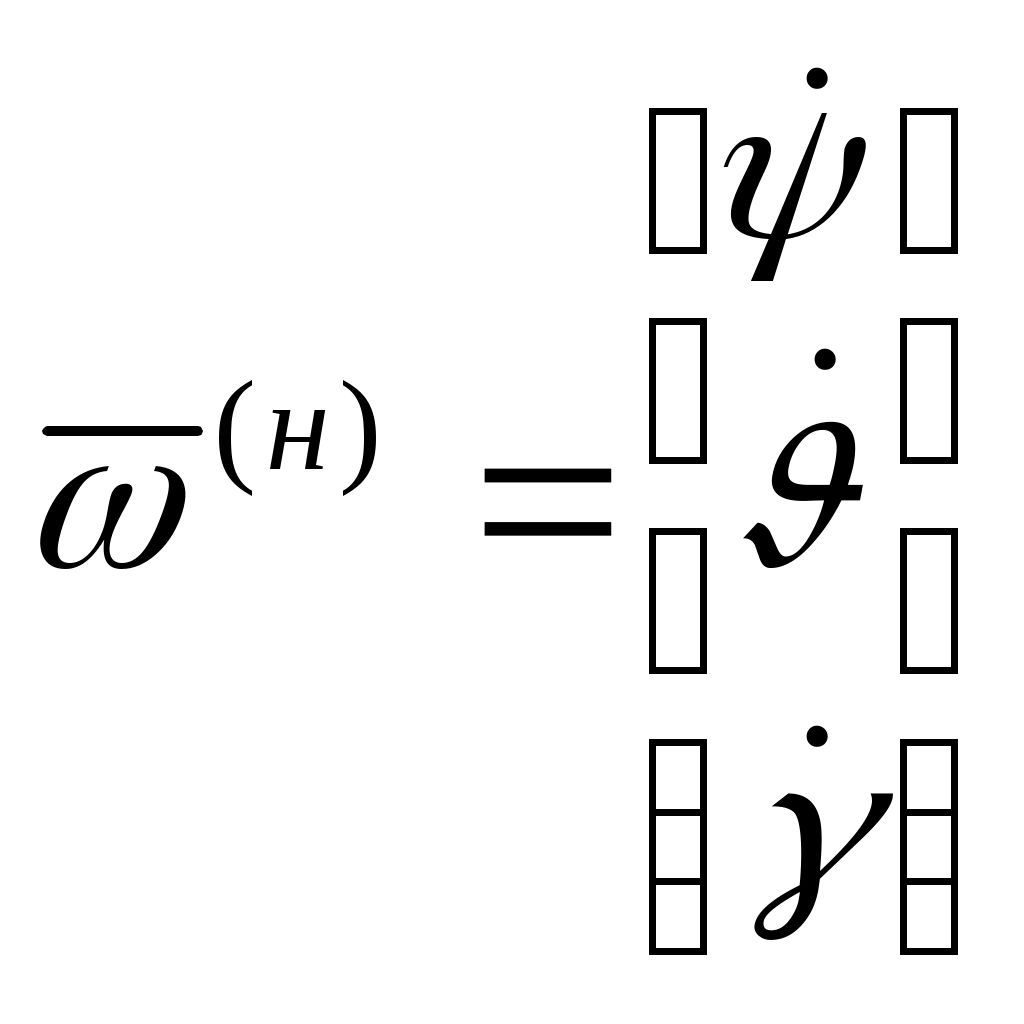
Из рис. 5 видно, что
Отсюда запишем матрицу перехода от непрямоугольной системы к связанной:
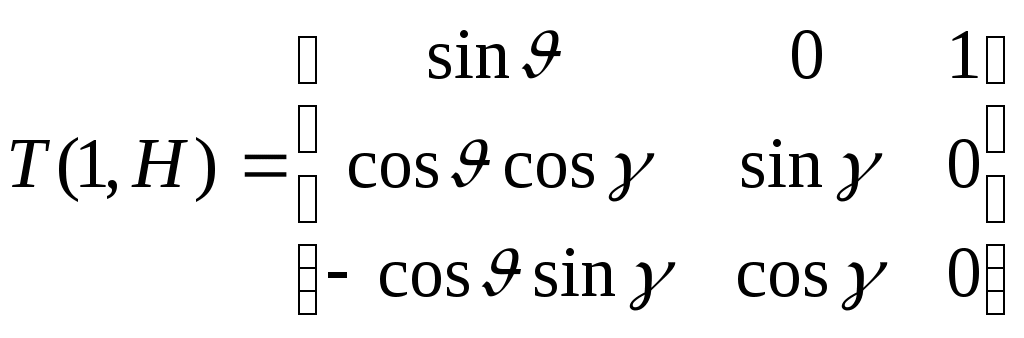
Обычно требуется провести обратное преобразование T(H,1), которое находят по обычным правилам вычисления обратных матриц:
Нетрудно видеть, что определитель
Запишем взаимную матрицу
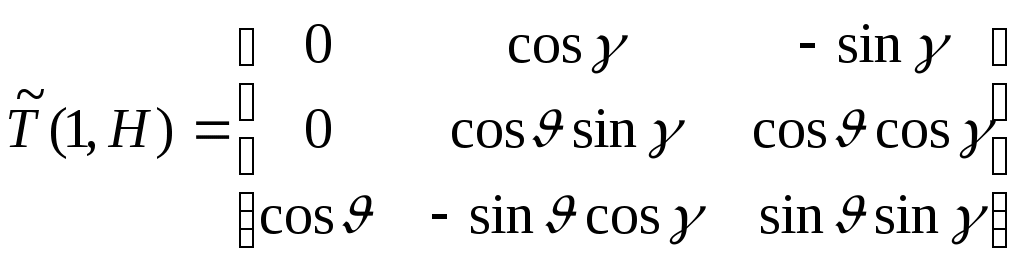 .
.Таким образом, связь между проекциями угловой скорости в разных базисах выражается следующими уравнениями:
Поскольку уравнения движения центра масс (1), (2), (3) записаны в траекторных осях, уравнения вращательного движения вокруг центра масс (4) – (9) – в связанных осях, а аэродинамические силы и моменты в правых частях уравнений (1) – (6) зависят от углов атаки