ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 89
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,  . Попробуем найти матрицу перехода от нормальной системы координат к скоростной. Перейдем сначала от нормальной системы координат к связанной, потом от связанной к скоростной, определив обратную матрицу к известной нам матрице перехода от скоростной к связанной системе координат:
. Попробуем найти матрицу перехода от нормальной системы координат к скоростной. Перейдем сначала от нормальной системы координат к связанной, потом от связанной к скоростной, определив обратную матрицу к известной нам матрице перехода от скоростной к связанной системе координат:
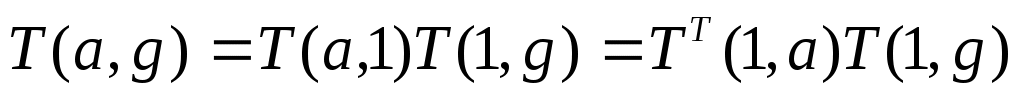 .
.
Матрица T(a,g) нами получена выше. Найдем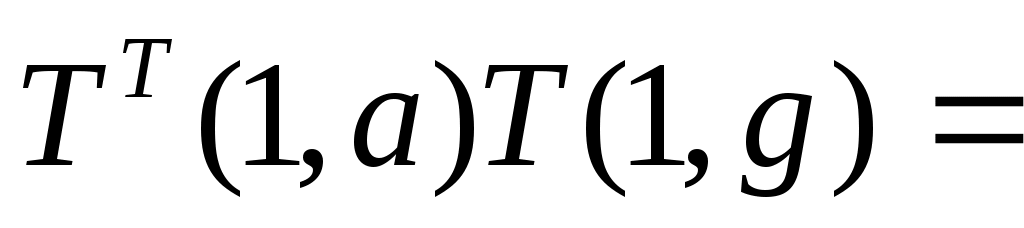
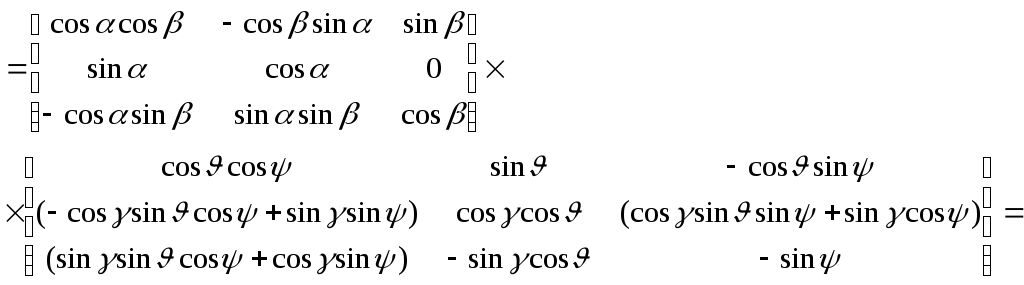

В силу свойств ортогональных матриц, связывающих их элементы равенствами, остаются независимыми три равенства, составляемые из элементов матриц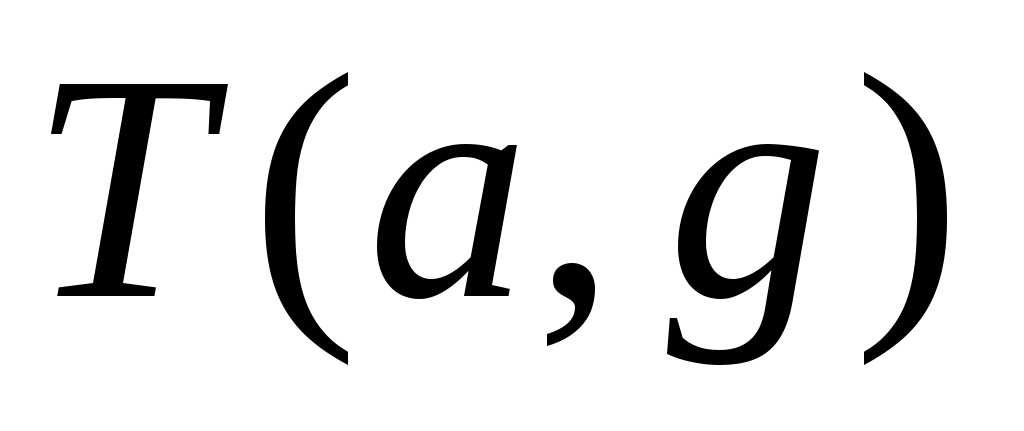 и
и 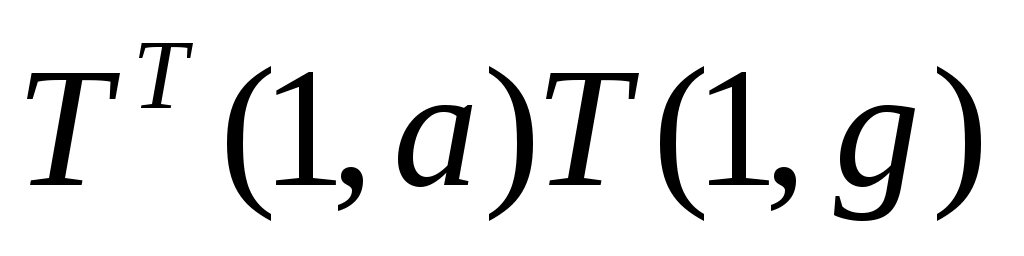 с индексами
с индексами 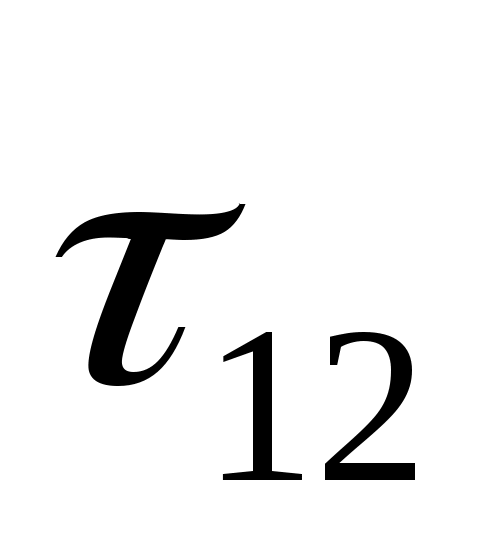 ,
,  ,
,  . Запишем эти уравнения геометрической связи углов
. Запишем эти уравнения геометрической связи углов  ,
,  ,
,  и
и  ,
,  ,
,  ,
,  ,
,  :
:
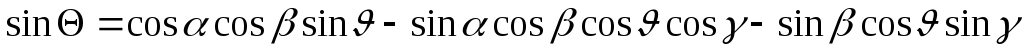 ; (10)
; (10)
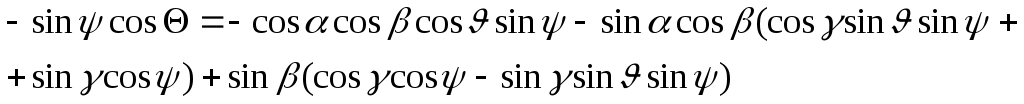 ; (11)
; (11)
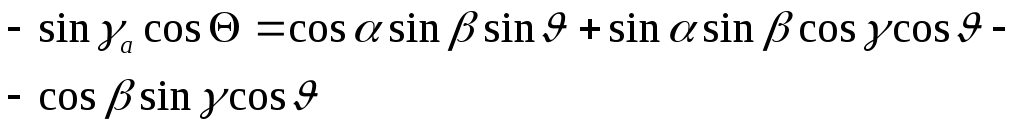 ; (12)
; (12)
Дополним эту систему уравнениями
, задающими проекции линейной скорости ЛА в нормальных осях координат. Используем при этом матрицу перехода от нормальной к траекторной системе:
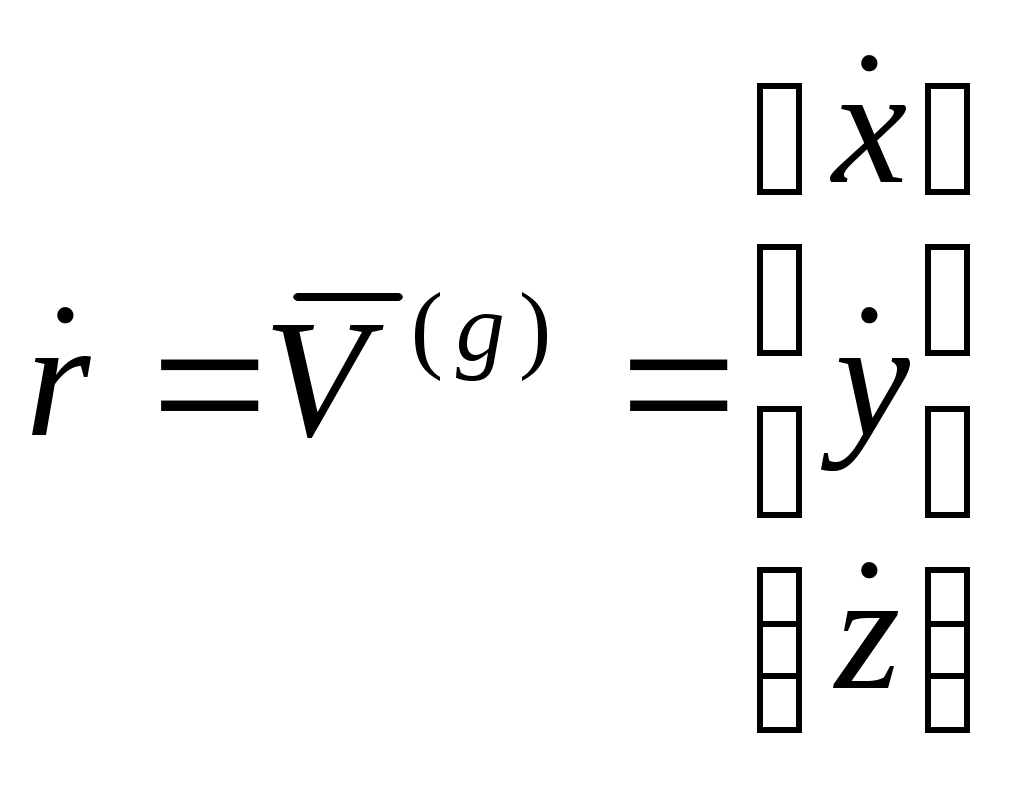 ;
; 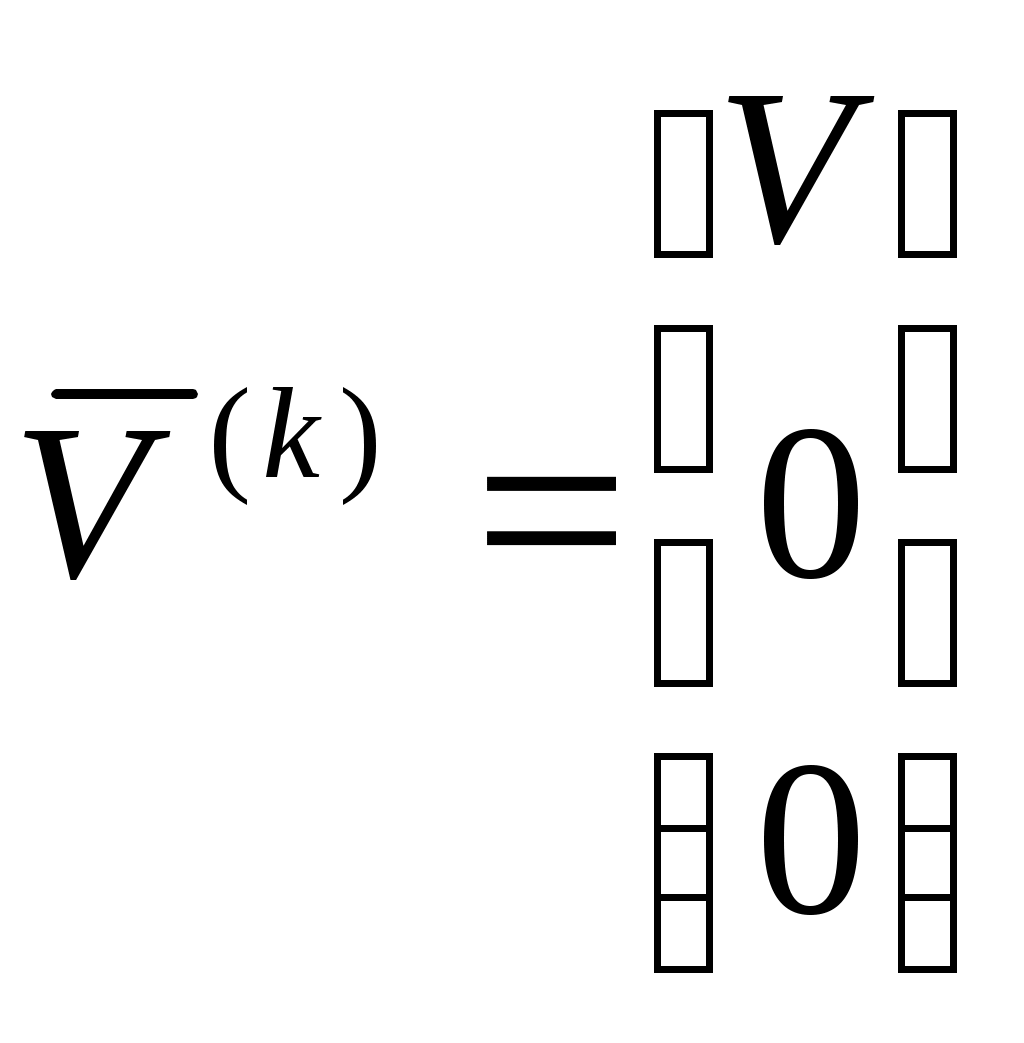 ;
; 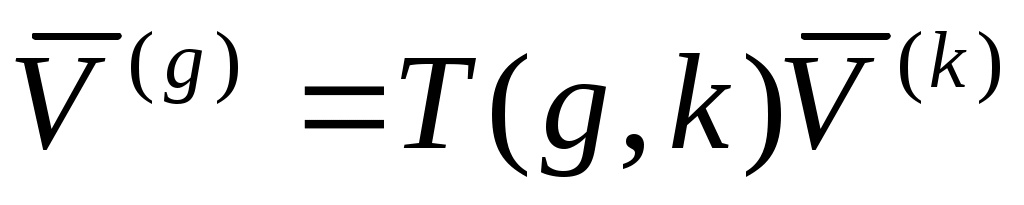 ;
;
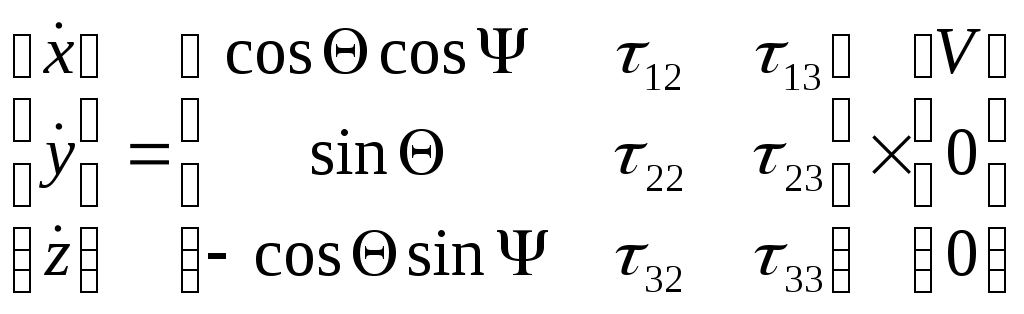
Итак, уравнения движения центра масс в нормальных осях выразятся так:
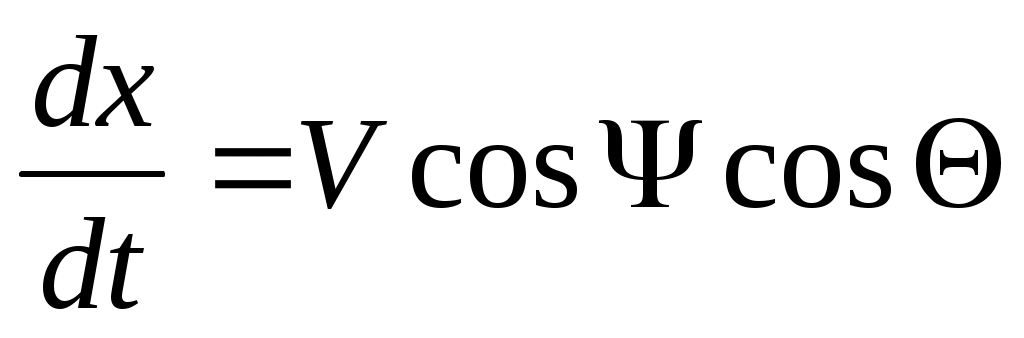 ; (13)
; (13)
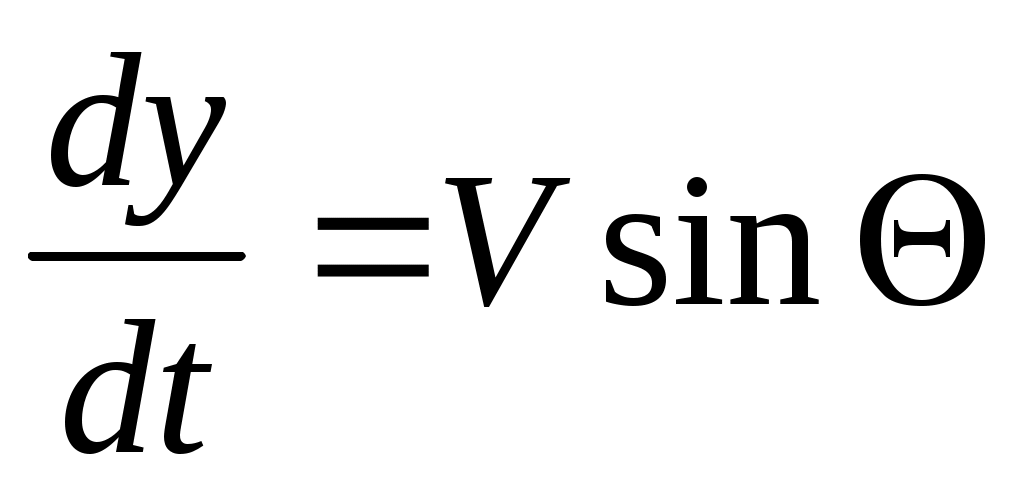 ; (14)
; (14)
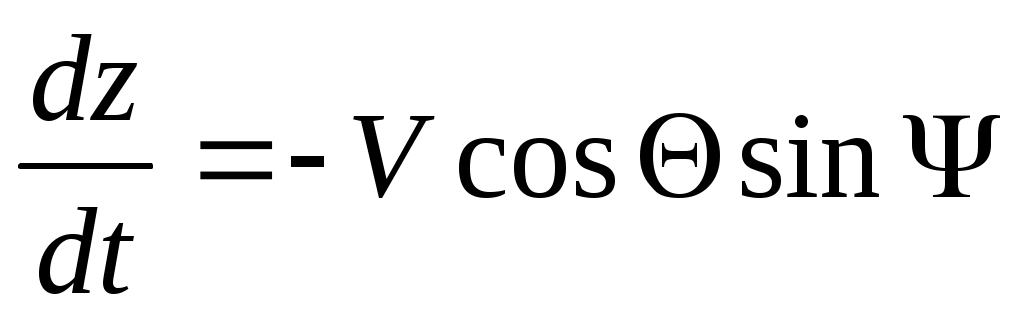 ; (15)
; (15)
Дадим последнее уравнение – уравнение тяги двигателя:
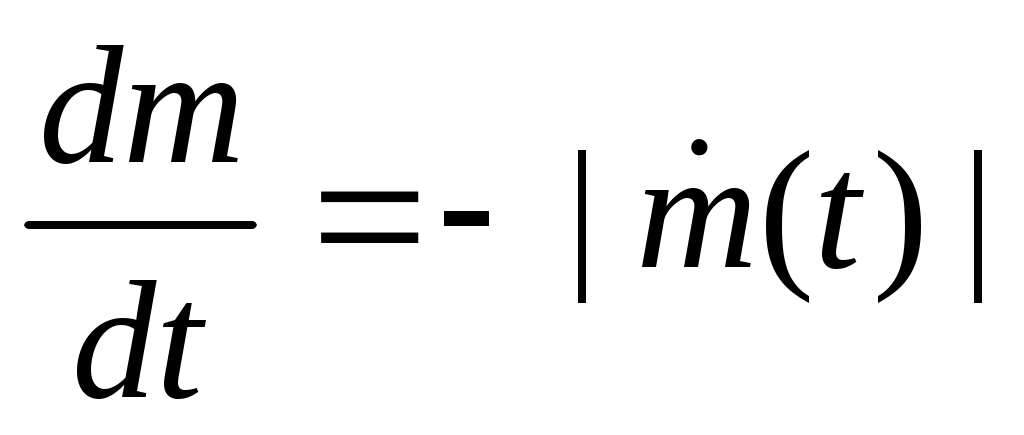 , (16)
, (16)
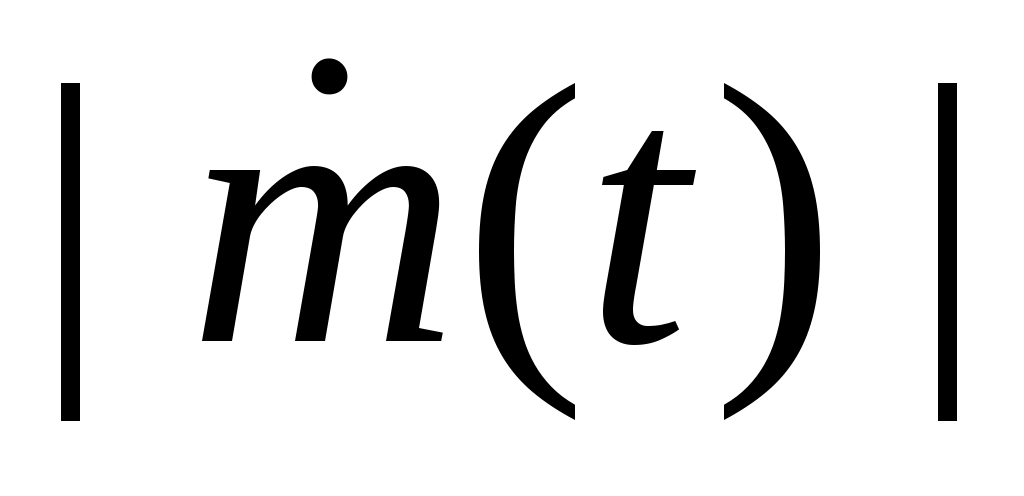 – секундный расход топлива.
– секундный расход топлива.
Поскольку Земля имеет сферическую форму, необходимо задать функцию высоты от текущих координат ЛА в нормальной системе координат
H=H(x,y,z).
Если сферичностью пренебречь, что допустимо для траекторий движения ЛА широкого класса, то можно считать, что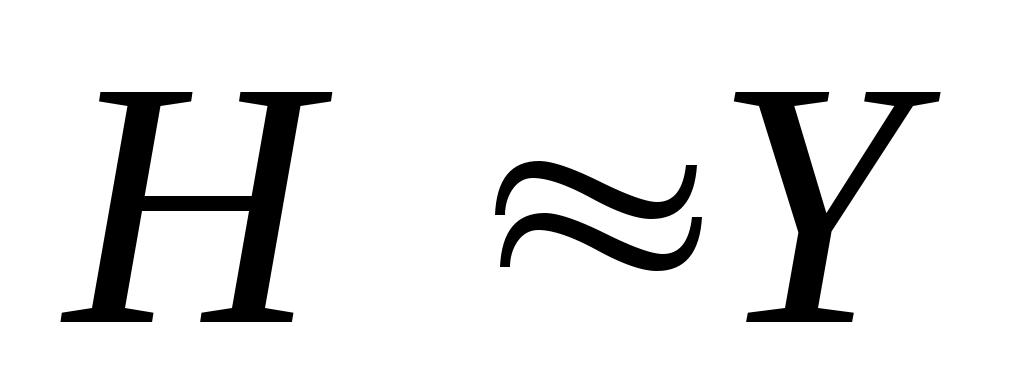 . (В дальнейшем так и будем полагать.)
. (В дальнейшем так и будем полагать.)
Из аэродинамики известно [5], что аэродинамические силы и моменты, входящие в уравнения (1) – (6), могут быть вычислены по формулам:
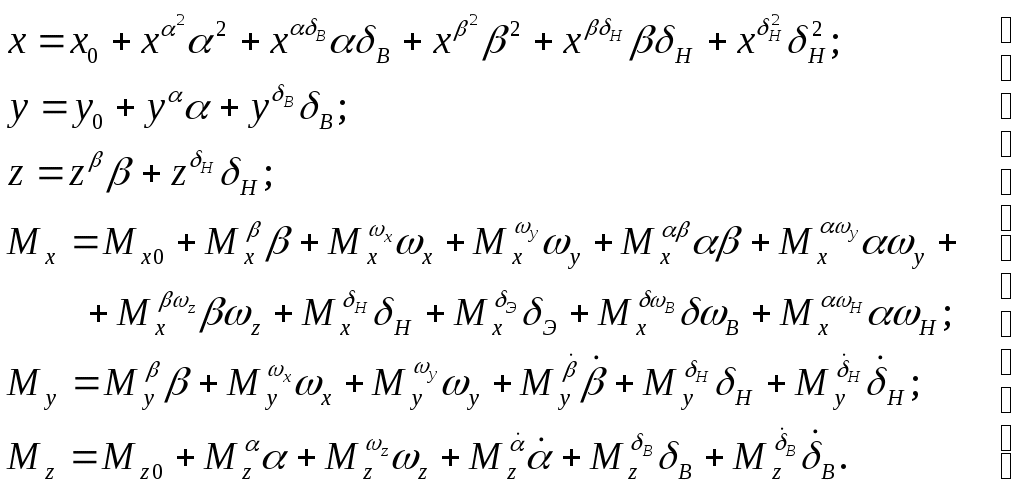 (17)
(17)
Здесь
x0 – значение x при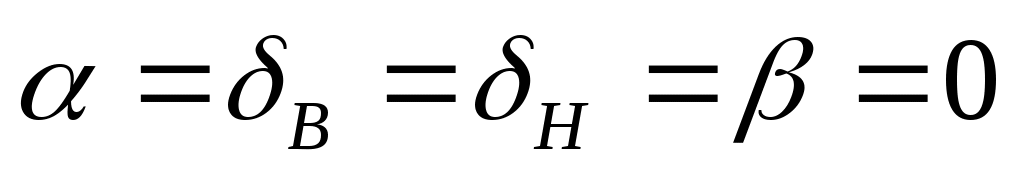 ;
;
y0 – значение y при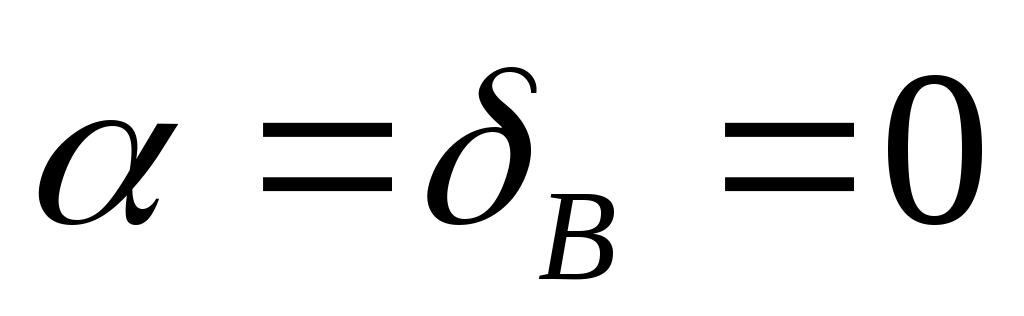 ;
;
Mx0 – значение Mx при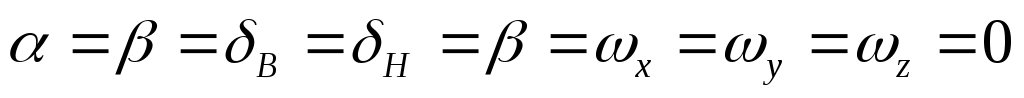
Mx0 – значение Mx при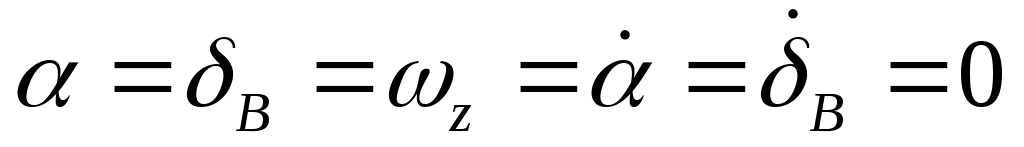
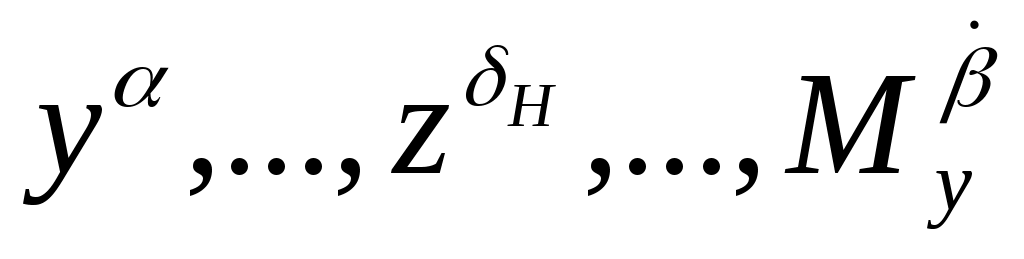 1 – частные производные от сил и моментов по соответствующим параметрам.
1 – частные производные от сил и моментов по соответствующим параметрам.
Полученная система уравнений (1) – (16) содержит 13 дифференциальных уравнений первого порядка и три геометрических соотношения.
В случае неуправляемого полета или полета с зафиксированными органами управления данная система является замкнутой, т. е. число неизвестных переменных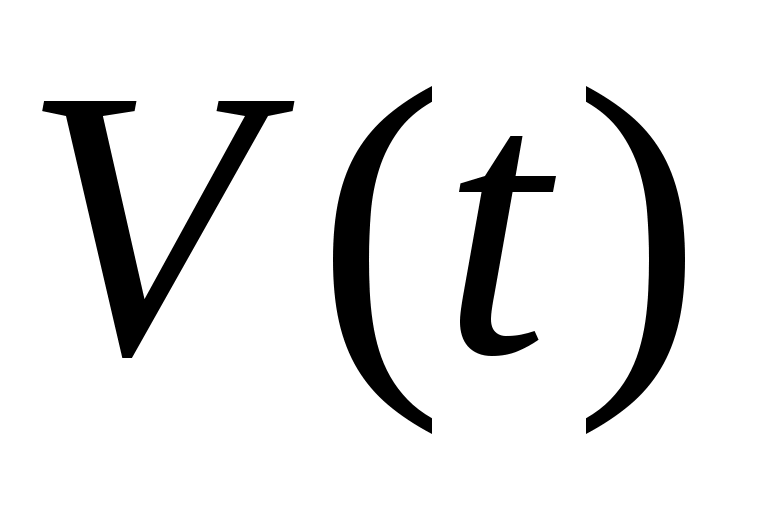 ,
, 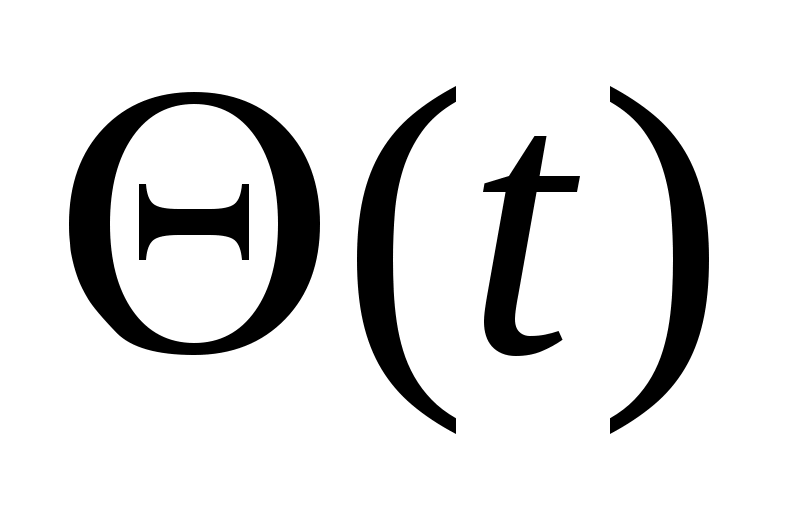 ,
, 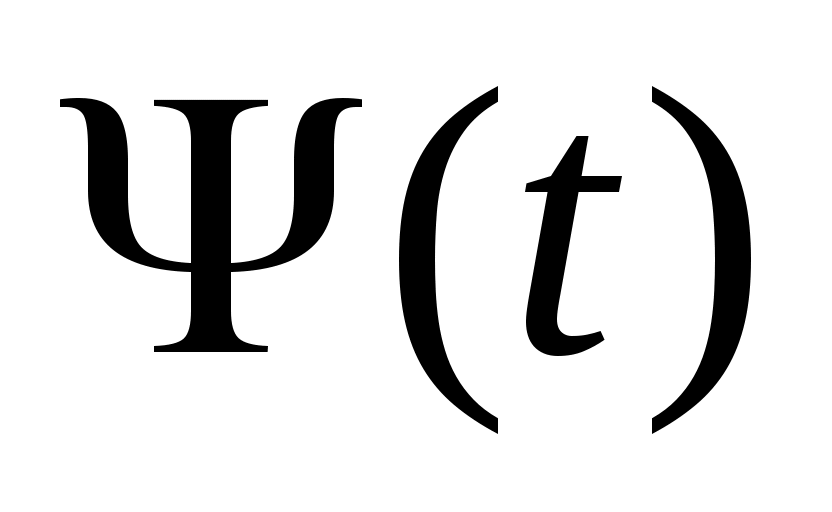 ,
, 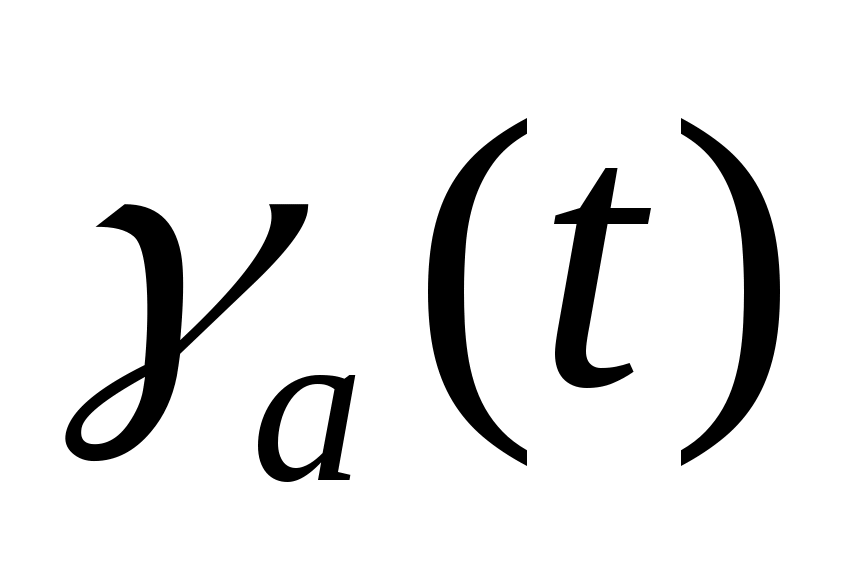 ,
, 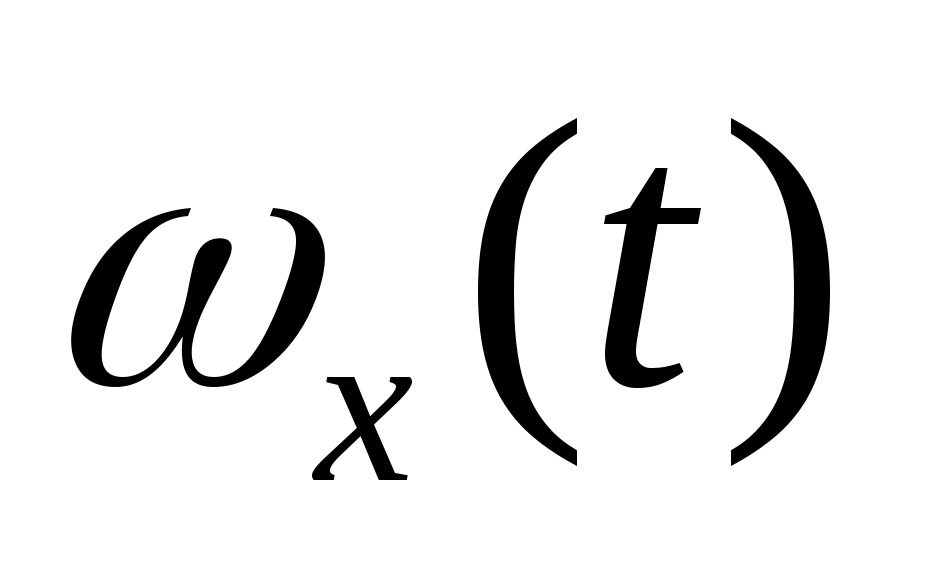 ,
, 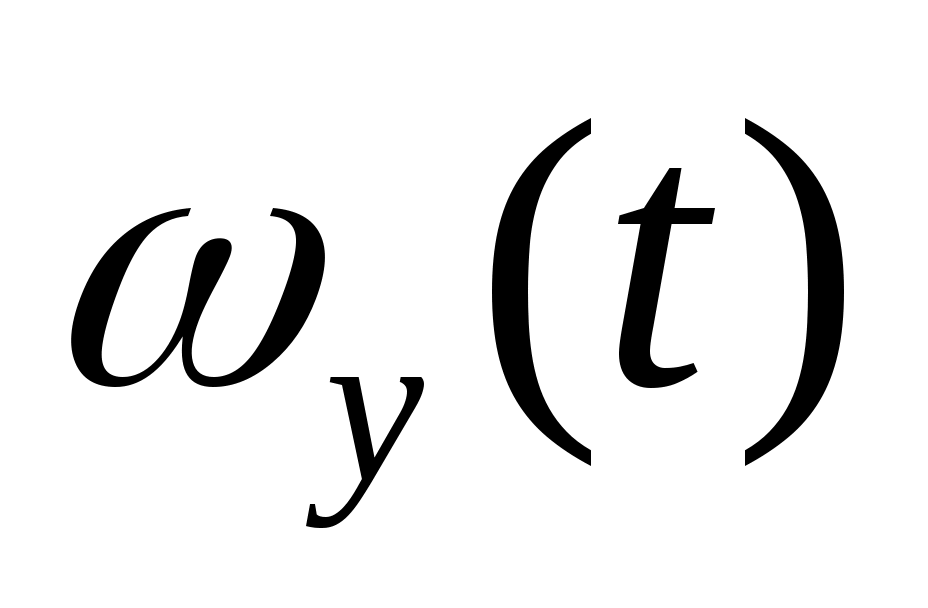 ,
, 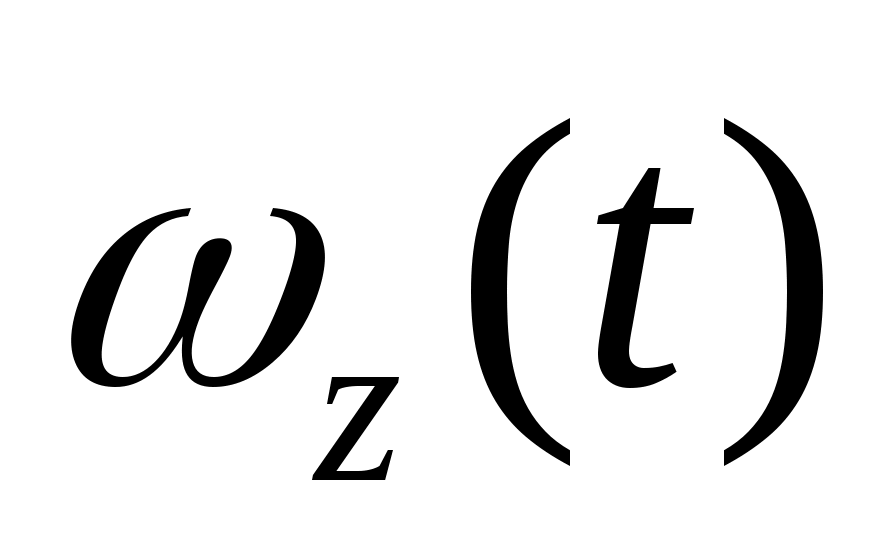 ,
, 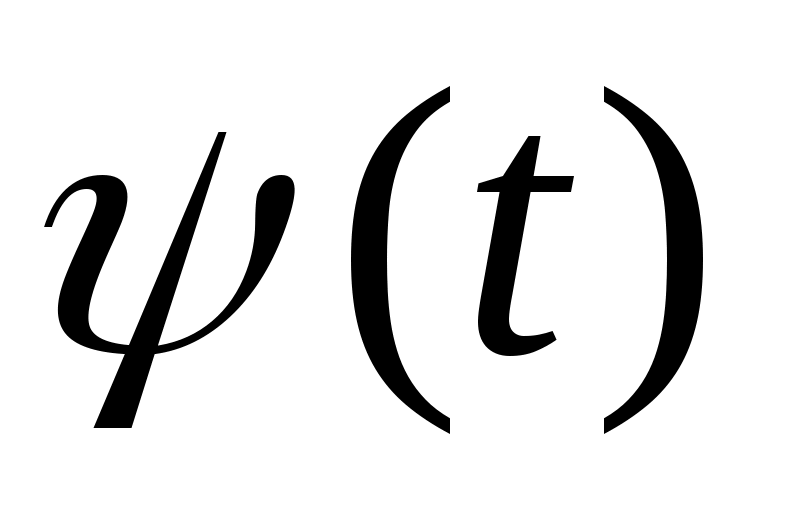 ,
, 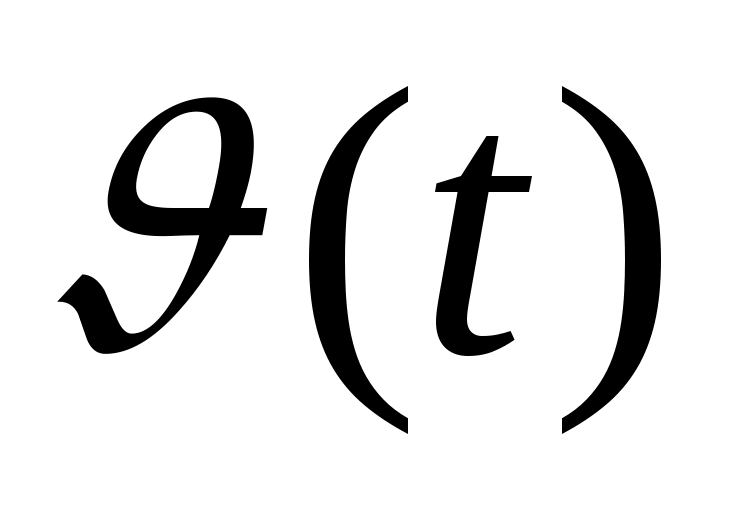 ,
, 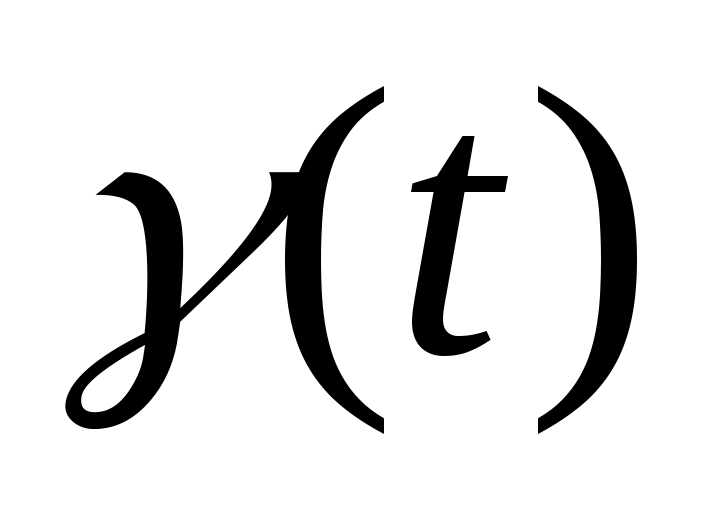
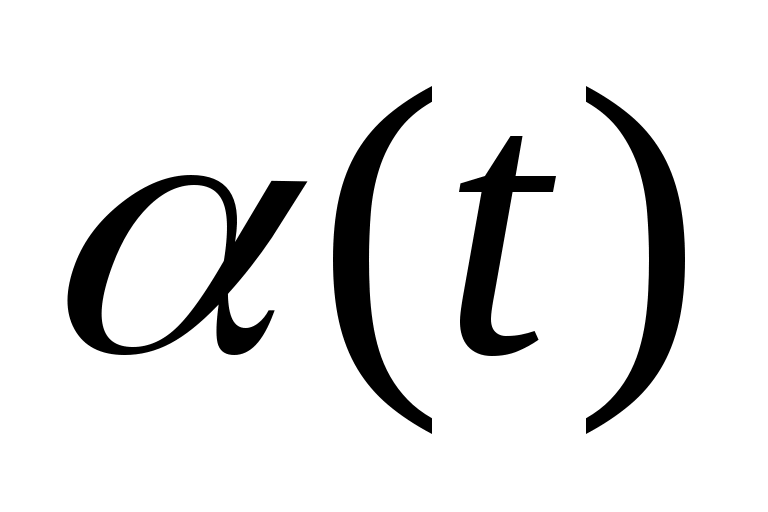 ,
, 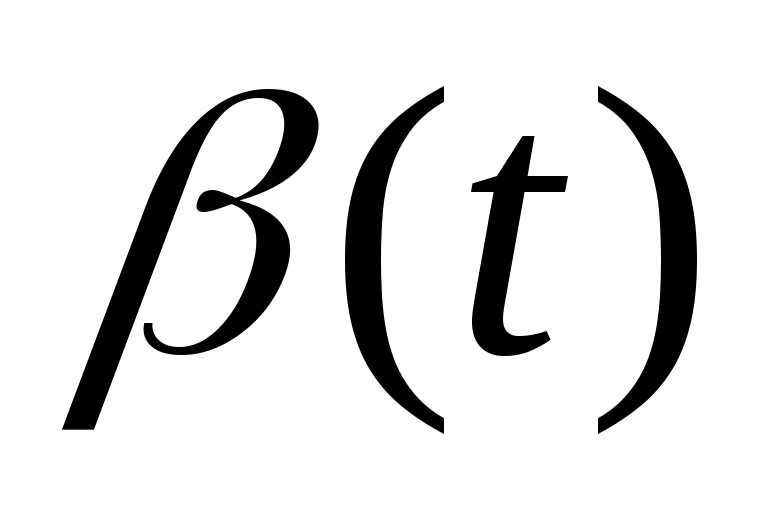 ,
, 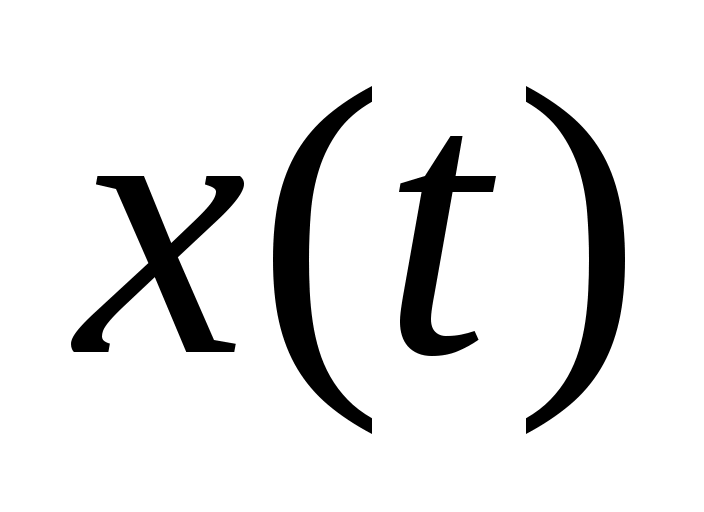 ,
, 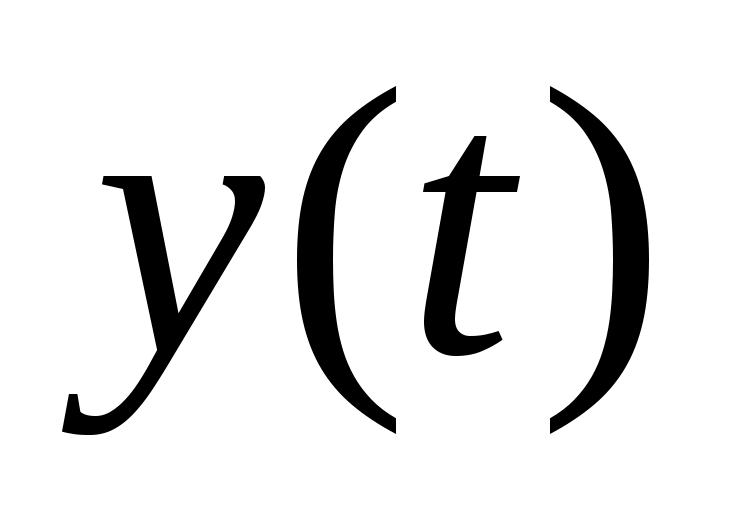 ,
, 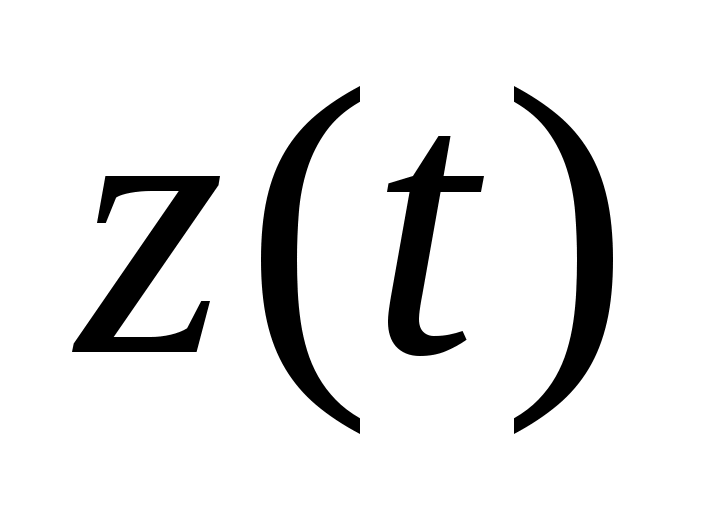 ,
, 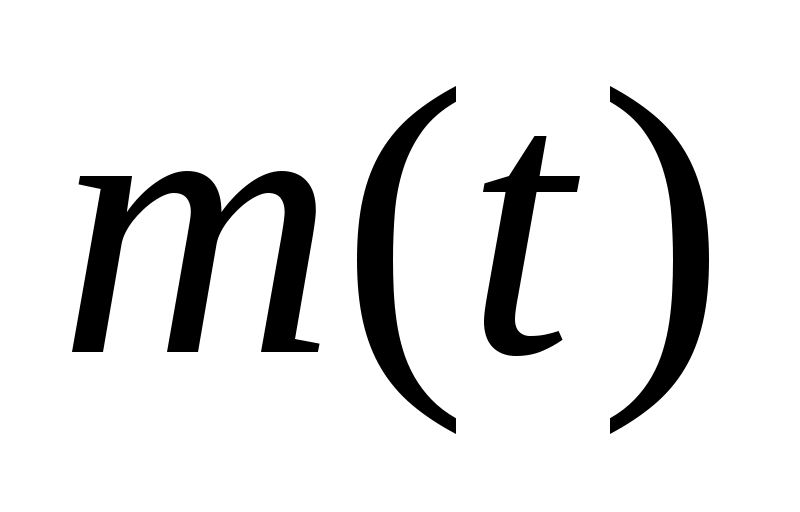 равно числу уравнений. И в идеальном случае (при отсутствии возмущений) траектория полета полностью определяется начальными условиями.
равно числу уравнений. И в идеальном случае (при отсутствии возмущений) траектория полета полностью определяется начальными условиями.
В случае управляемого полета данная система уравнений не является замкнутой, так как проекции аэродинамических сил и моментов в правых частях уравнений будут зависеть от углов отклонения органов управления:
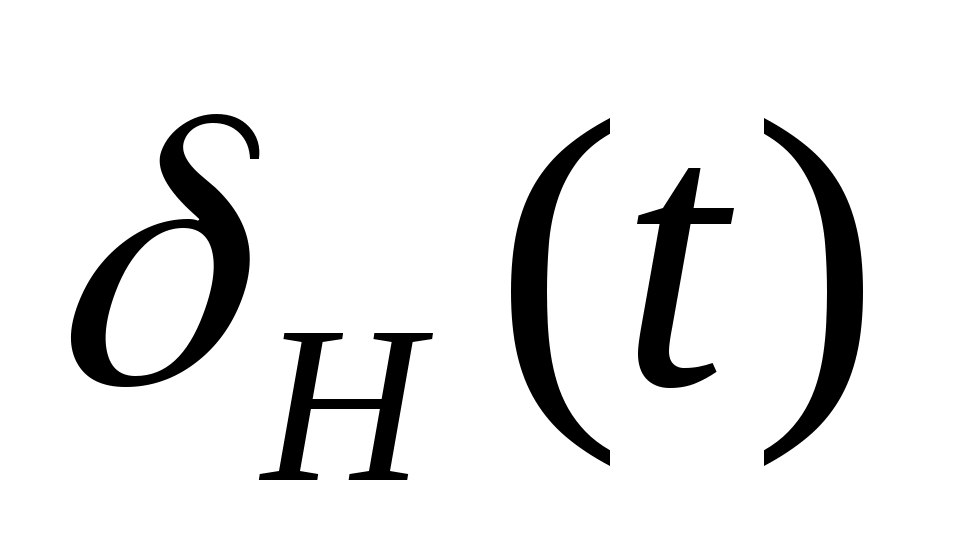 – отклонение рулей направления;
– отклонение рулей направления;
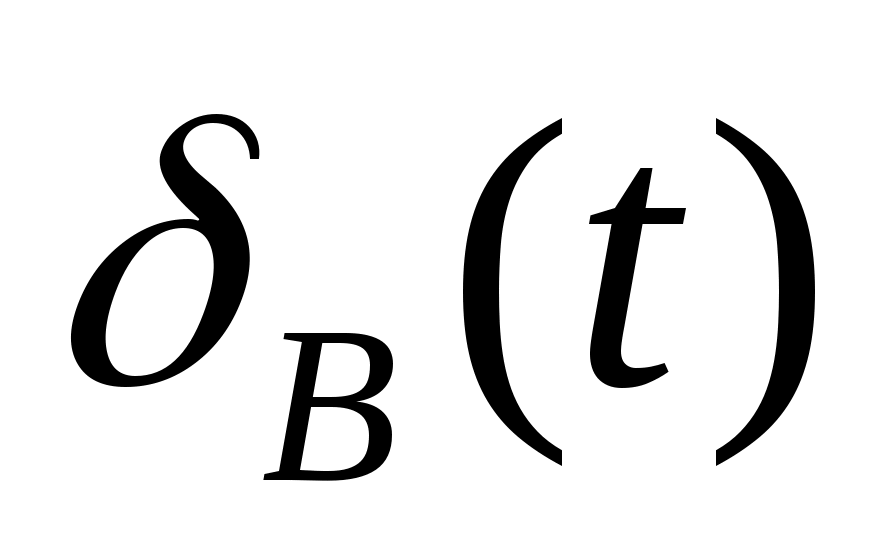 – отклонение рулей высоты;
– отклонение рулей высоты;
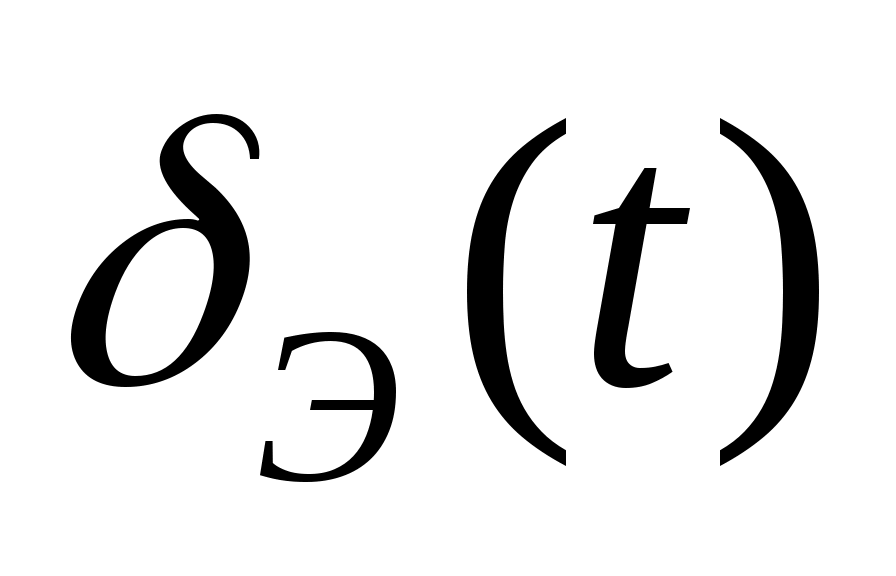 – отклонение элеронов;
– отклонение элеронов;
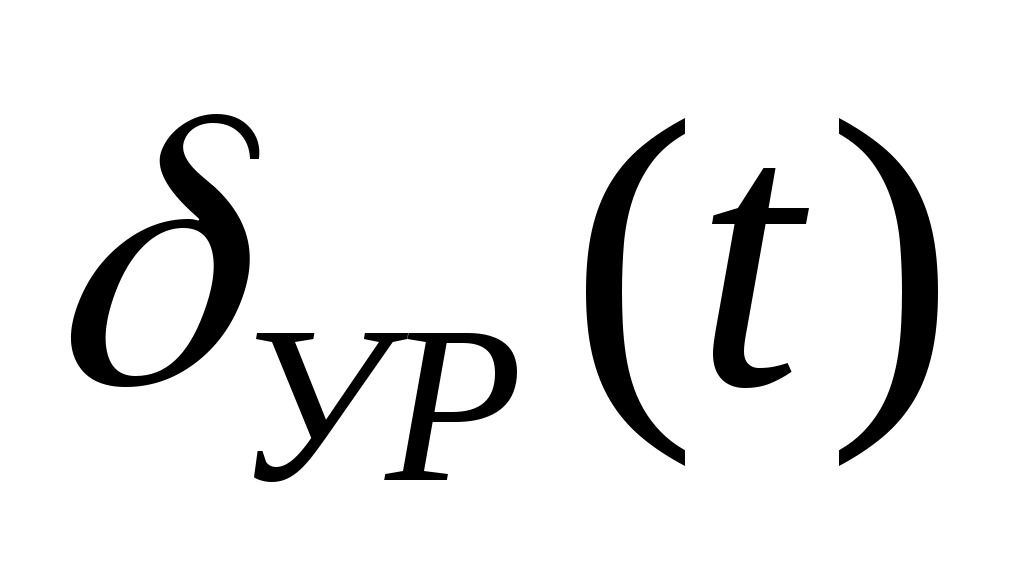 – отклонение органа регулировки тяги двигателя.
– отклонение органа регулировки тяги двигателя.
Если задать отклонения органов управления как известные функции времени, то при заданных начальных условиях и номинальных значениях параметров аппарата будет определена единственная траектория движения ЛА, которую назовем траекторией невозмущенного движения.
На самом деле в реальном полете отклонение органов управления осуществляется от программного устройства через автопилот. И вообще бортовая система управления должна обеспечивать вполне определенную функциональную связь между отклонениями органов управления и текущими значениями параметров полета:
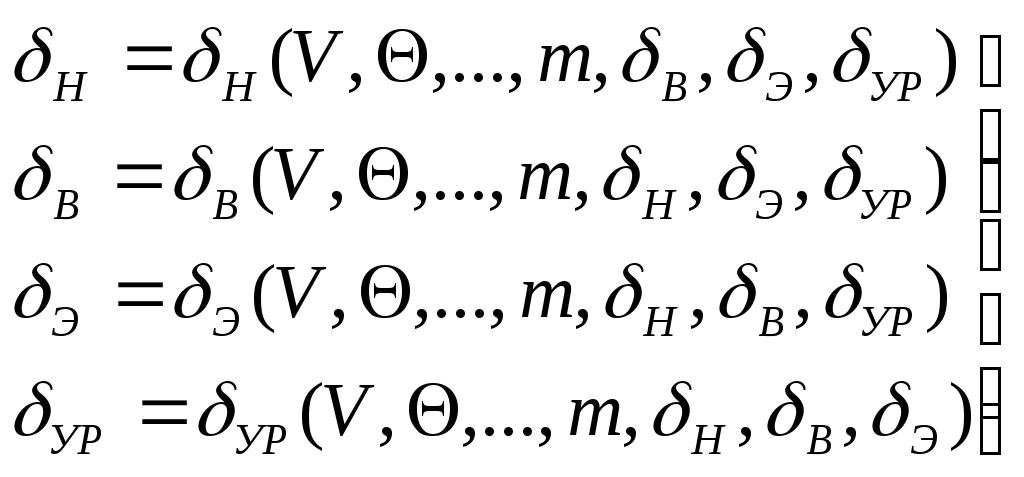 (18)
(18)
С учётом этого требования система уравнений (1) – (16), (18) становится замкнутой и для управляемого полета.
В действительном полете начальные условия всегда отличаются от заданных, на ЛА действуют в случае аэродинамические силы, связанные с турбулентностью атмосферы, система управления отрабатывает требуемую функциональную связь (18) параметров полета, с некоторыми, вообще говоря, случайными ошибками. Поэтому параметры полета всегда отличаются от их теоретического значения, а реальную траекторию называют траекторией возбужденного движения.
§ 4. Линеаризация уравнений движения летательного аппарата
Система уравнений движения ЛА является сложной нелинейной системой дифференциальных уравнений.
Основным методом исследования таких уравнений является из интегрирование с помощью ЦВМ. В то же время при проектировании системы управления имеется настоятельная необходимость аналитического представления динамических и кинематических характеристик ЛА. Поэтому используют различные методы упрощения уравнений движения, что делает доступным аналитические методы исследования динамики полета. Одним из таких упрощений является линеаризация этих уравнений относительно малых отклонений параметров движения. Параметры возмущенного движения обычно определяют методами численного интегрирования с помощью ЦВМ как известные функции времени:
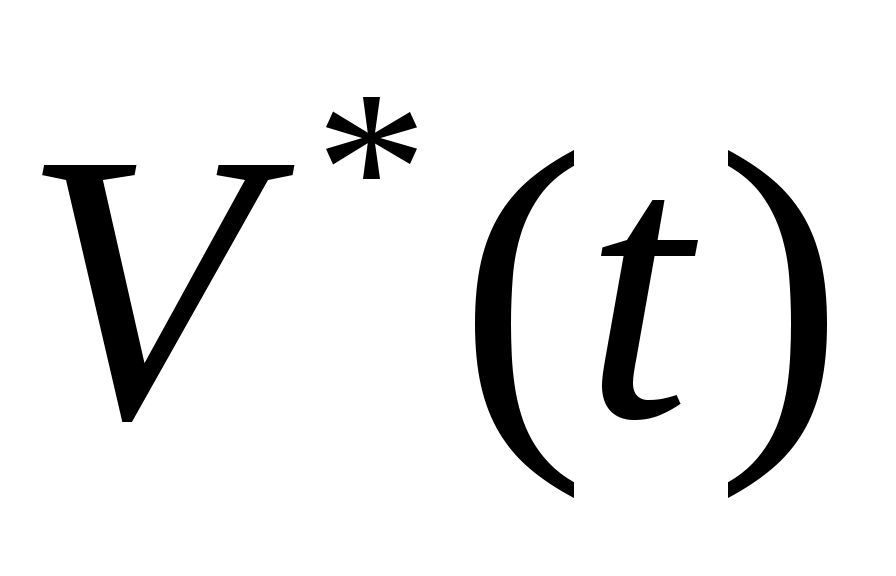 ;
; 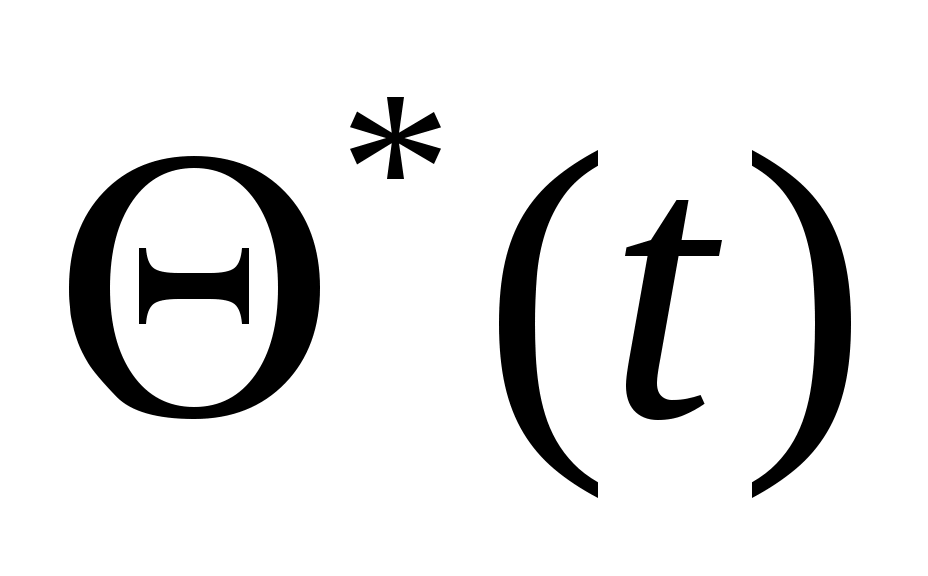 ,
, 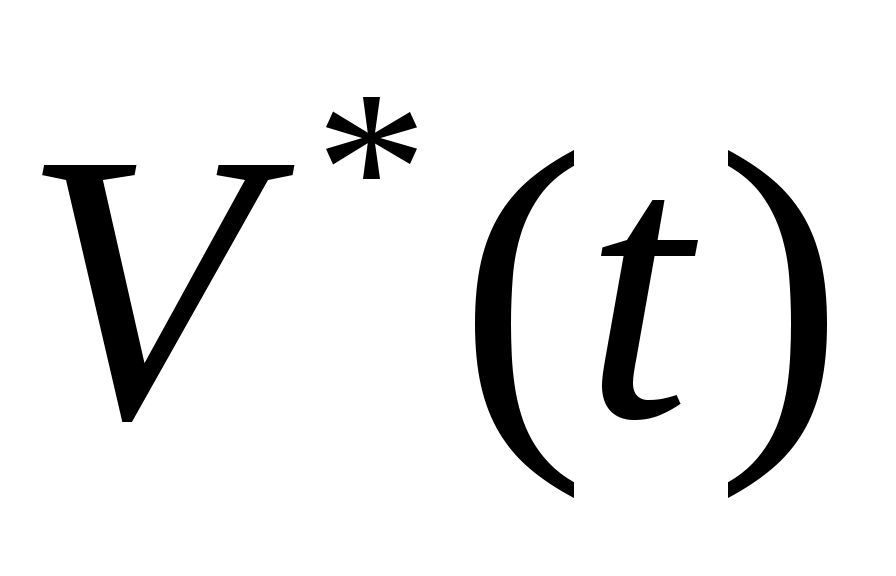 и т.д.
и т.д.
Параметры возмущенного движения отличаются от параметров невозмущенного движения на некоторую малую величину: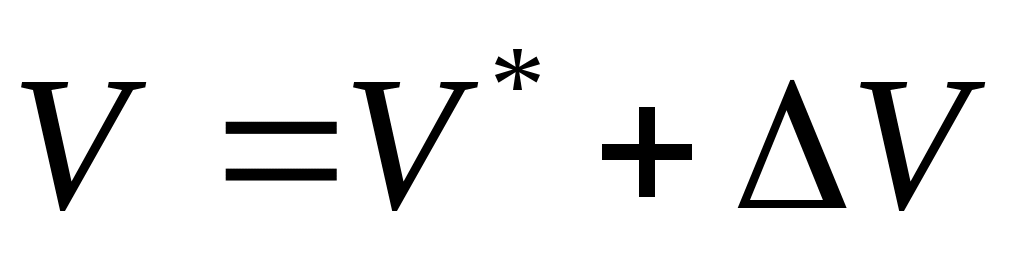 ;
; 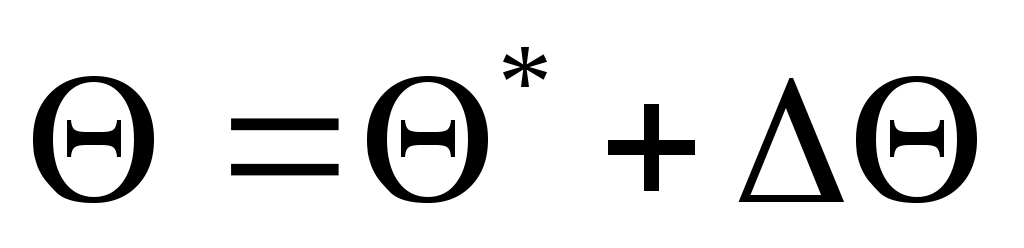 ;
; 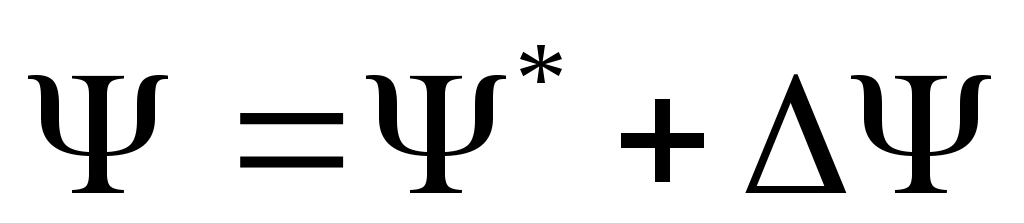 ;
; 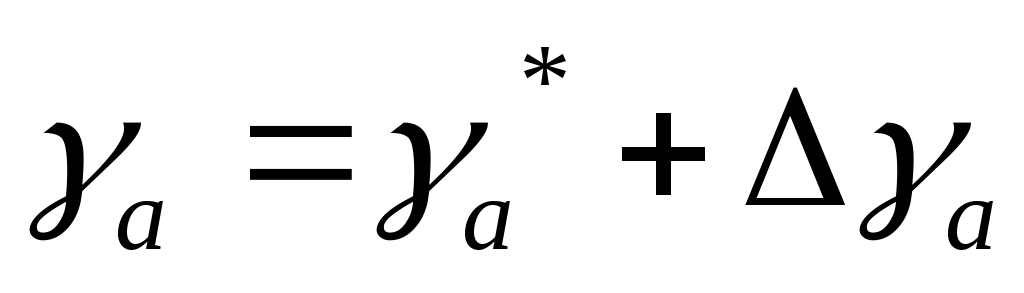 и т. Д.
и т. Д.
1. С целью упрощения получаемых линеаризованных уравнений, учитывая, что в невозмущённом движении углы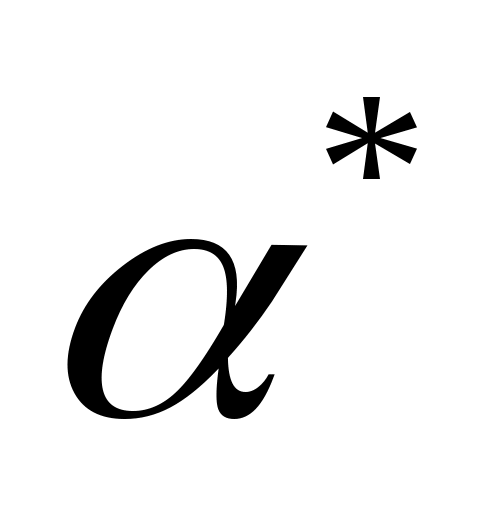 ,
, 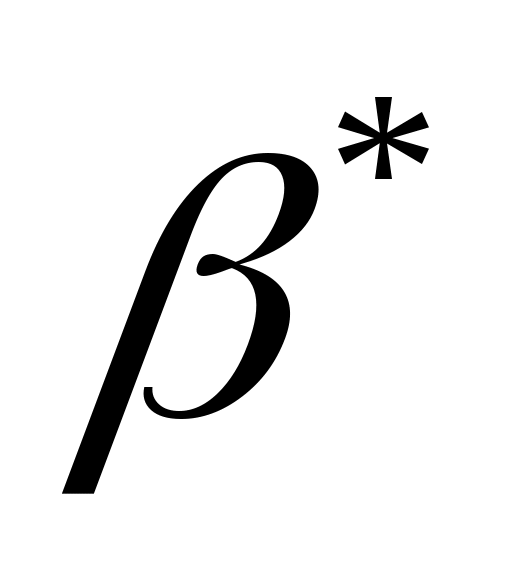 обычно невелики, полагает, что
обычно невелики, полагает, что  ,
, 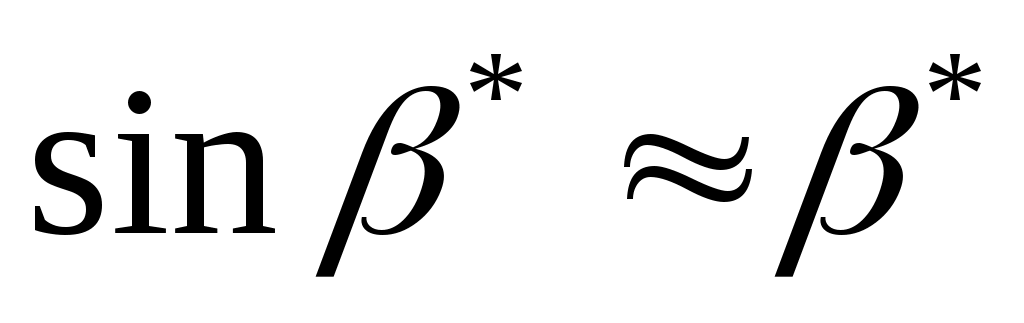 ;
; 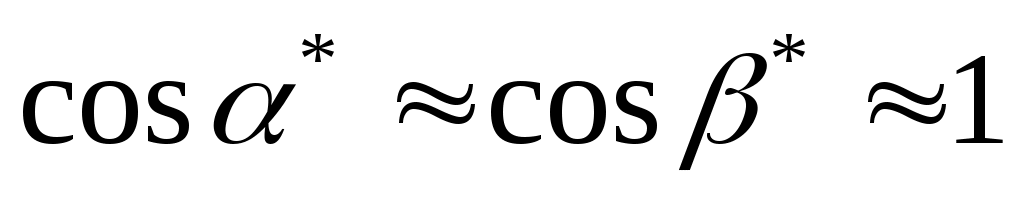 .
.
2. Будем считать, что изменения массы в возмущенном и в невозмущенном движениях одинаковы и являются известными функциями времени.
3. Предполагаем также, что в невозмущенном движении кинематические параметры бокового движения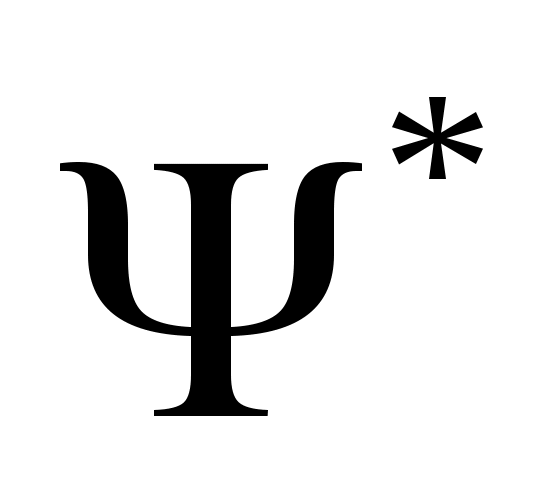
Матрица T(a,g) нами получена выше. Найдем
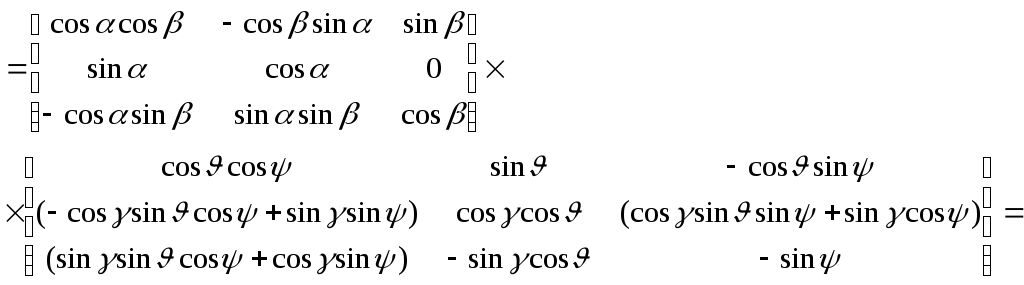

В силу свойств ортогональных матриц, связывающих их элементы равенствами, остаются независимыми три равенства, составляемые из элементов матриц
Дополним эту систему уравнениями
, задающими проекции линейной скорости ЛА в нормальных осях координат. Используем при этом матрицу перехода от нормальной к траекторной системе:
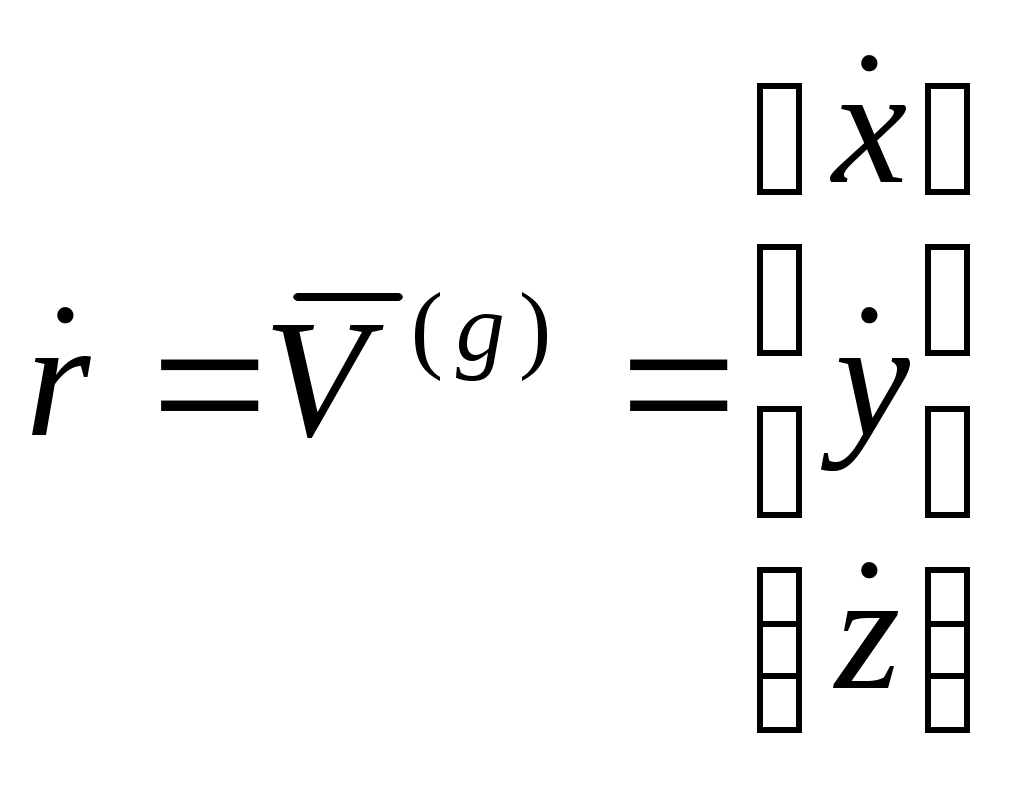 ;
; 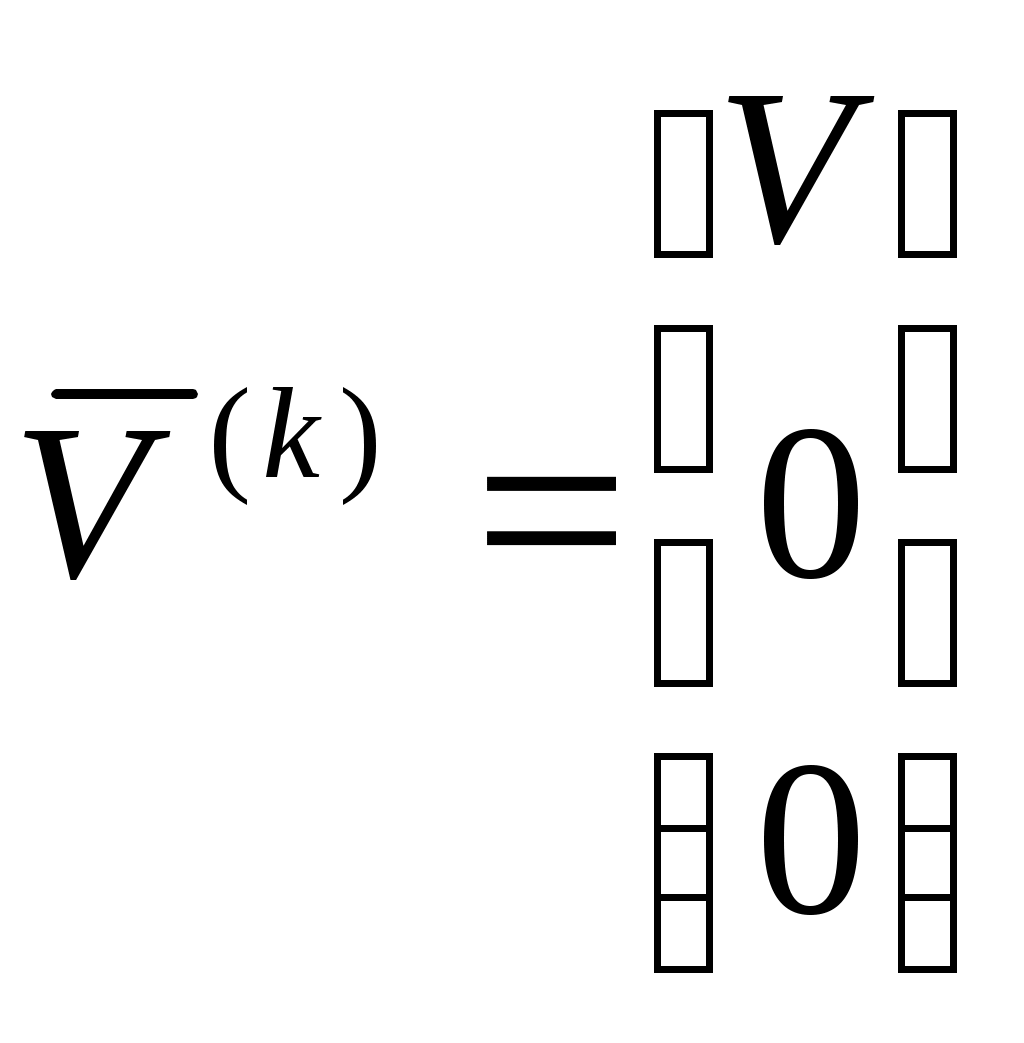 ;
; 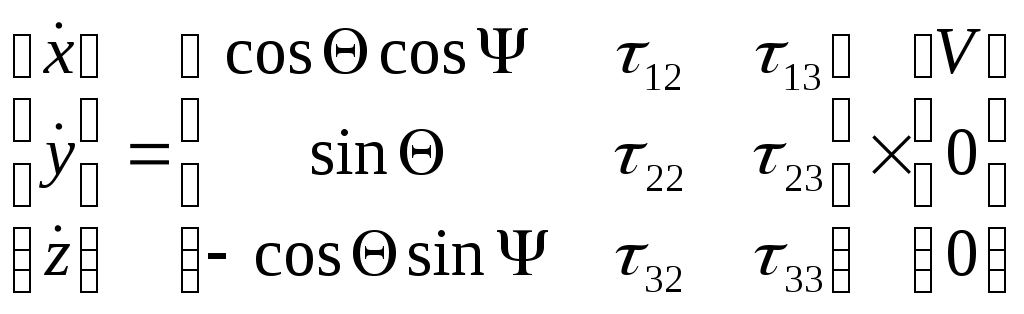
Итак, уравнения движения центра масс в нормальных осях выразятся так:
Дадим последнее уравнение – уравнение тяги двигателя:
Поскольку Земля имеет сферическую форму, необходимо задать функцию высоты от текущих координат ЛА в нормальной системе координат
H=H(x,y,z).
Если сферичностью пренебречь, что допустимо для траекторий движения ЛА широкого класса, то можно считать, что
Из аэродинамики известно [5], что аэродинамические силы и моменты, входящие в уравнения (1) – (6), могут быть вычислены по формулам:
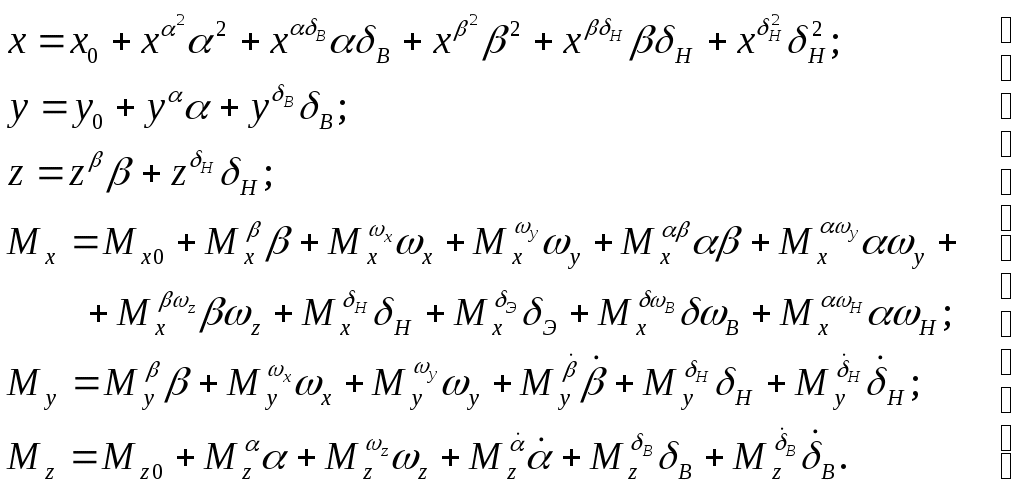 (17)
(17)Здесь
x0 – значение x при
y0 – значение y при
Mx0 – значение Mx при
Mx0 – значение Mx при
Полученная система уравнений (1) – (16) содержит 13 дифференциальных уравнений первого порядка и три геометрических соотношения.
В случае неуправляемого полета или полета с зафиксированными органами управления данная система является замкнутой, т. е. число неизвестных переменных
В случае управляемого полета данная система уравнений не является замкнутой, так как проекции аэродинамических сил и моментов в правых частях уравнений будут зависеть от углов отклонения органов управления:
Если задать отклонения органов управления как известные функции времени, то при заданных начальных условиях и номинальных значениях параметров аппарата будет определена единственная траектория движения ЛА, которую назовем траекторией невозмущенного движения.
На самом деле в реальном полете отклонение органов управления осуществляется от программного устройства через автопилот. И вообще бортовая система управления должна обеспечивать вполне определенную функциональную связь между отклонениями органов управления и текущими значениями параметров полета:
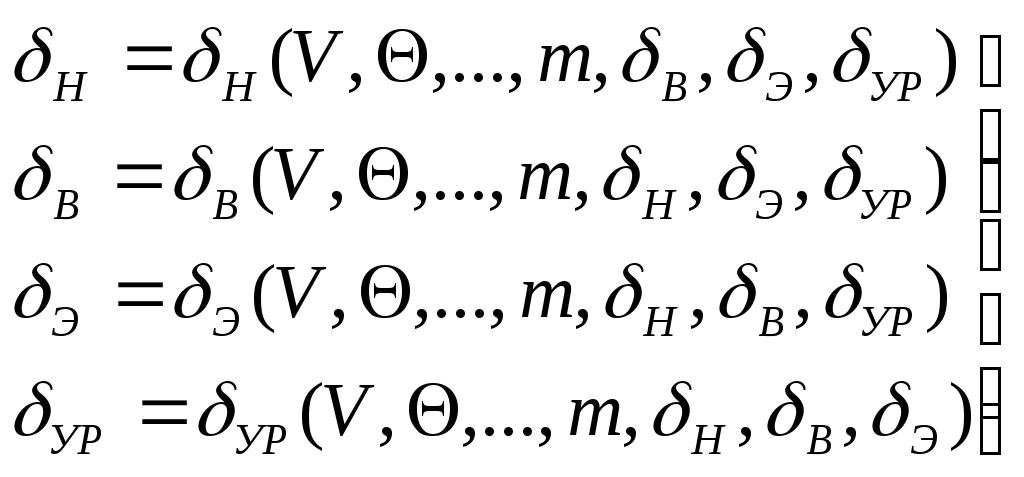 (18)
(18)С учётом этого требования система уравнений (1) – (16), (18) становится замкнутой и для управляемого полета.
В действительном полете начальные условия всегда отличаются от заданных, на ЛА действуют в случае аэродинамические силы, связанные с турбулентностью атмосферы, система управления отрабатывает требуемую функциональную связь (18) параметров полета, с некоторыми, вообще говоря, случайными ошибками. Поэтому параметры полета всегда отличаются от их теоретического значения, а реальную траекторию называют траекторией возбужденного движения.
§ 4. Линеаризация уравнений движения летательного аппарата
Система уравнений движения ЛА является сложной нелинейной системой дифференциальных уравнений.
Основным методом исследования таких уравнений является из интегрирование с помощью ЦВМ. В то же время при проектировании системы управления имеется настоятельная необходимость аналитического представления динамических и кинематических характеристик ЛА. Поэтому используют различные методы упрощения уравнений движения, что делает доступным аналитические методы исследования динамики полета. Одним из таких упрощений является линеаризация этих уравнений относительно малых отклонений параметров движения. Параметры возмущенного движения обычно определяют методами численного интегрирования с помощью ЦВМ как известные функции времени:
Параметры возмущенного движения отличаются от параметров невозмущенного движения на некоторую малую величину:
1. С целью упрощения получаемых линеаризованных уравнений, учитывая, что в невозмущённом движении углы
2. Будем считать, что изменения массы в возмущенном и в невозмущенном движениях одинаковы и являются известными функциями времени.
3. Предполагаем также, что в невозмущенном движении кинематические параметры бокового движения