ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 91
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 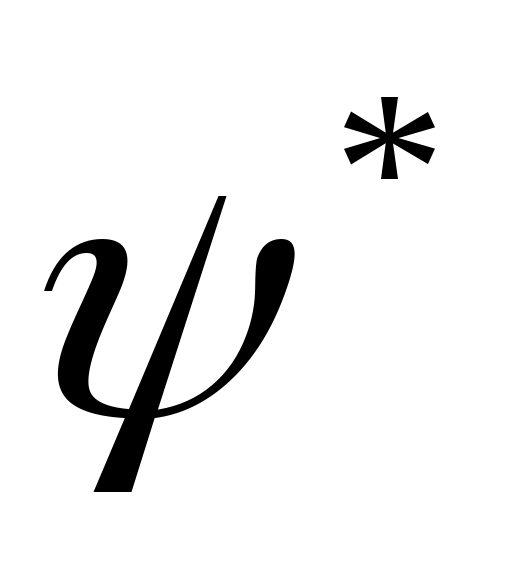 ,
,  ,
, 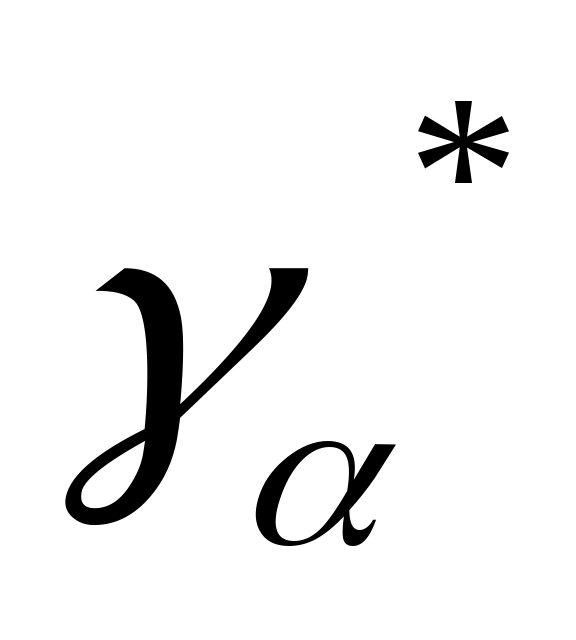 ,
, 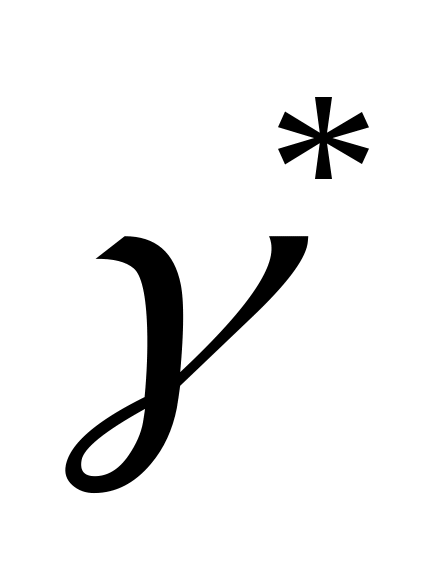 ,
, 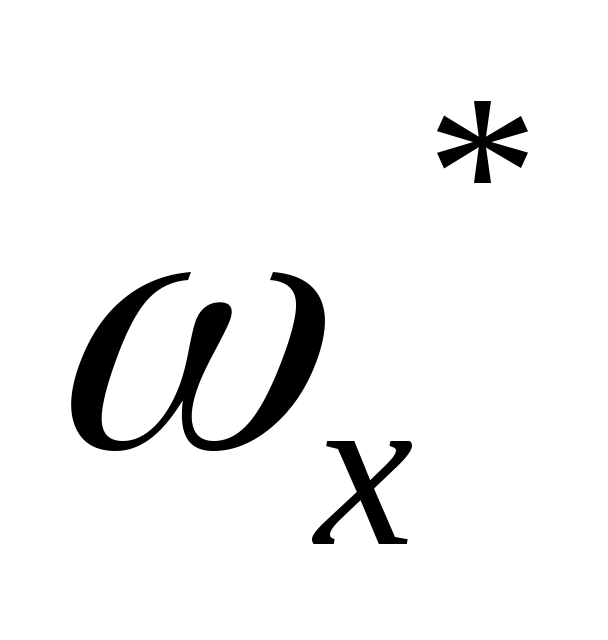 ,
, 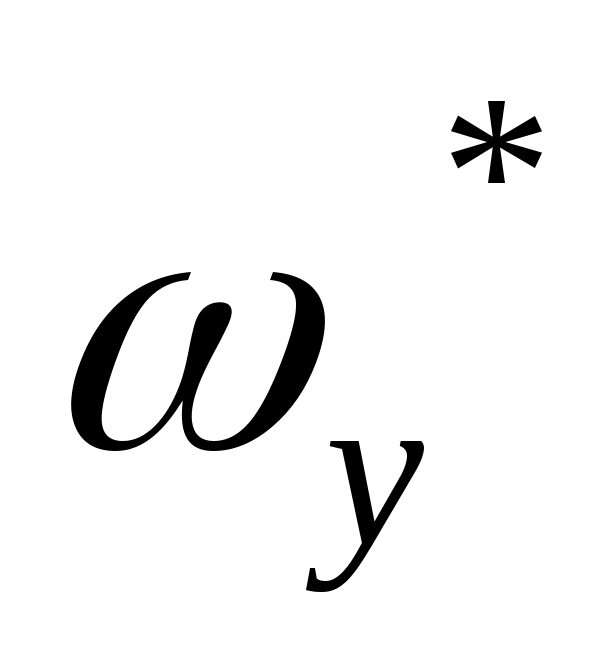 , а также отклонения органов управления боковым движением
, а также отклонения органов управления боковым движением  ,
, 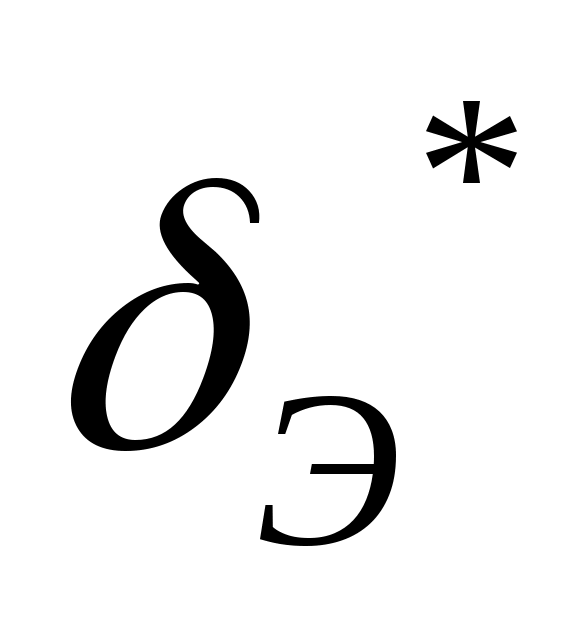 и производные по времени от продольных парамтров
и производные по времени от продольных парамтров 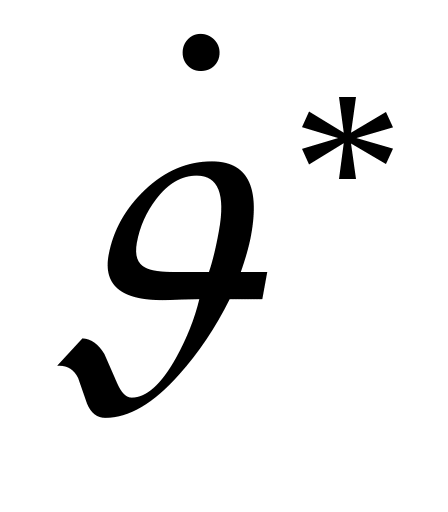 ,
, 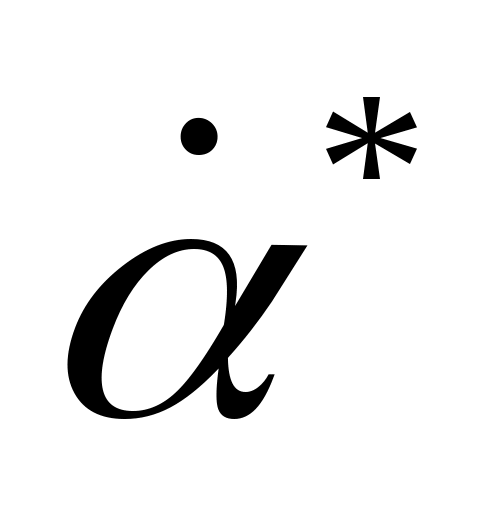 ,
,  ,
, 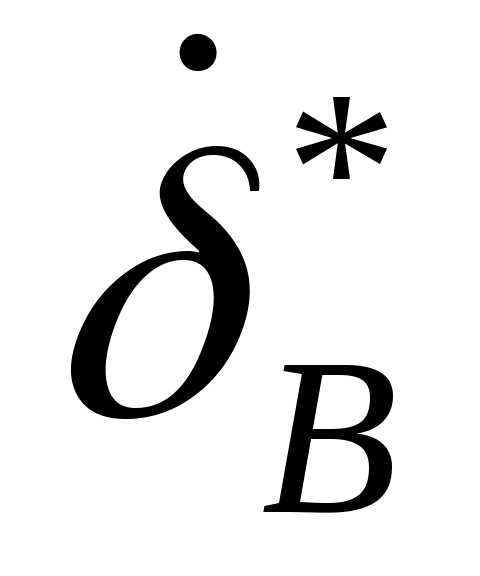 являются малыми, особенно для аппаратов, у которых применена стабилизация крена и траектория которых лежит в пределах небольшого пространственного угла.
являются малыми, особенно для аппаратов, у которых применена стабилизация крена и траектория которых лежит в пределах небольшого пространственного угла.
4. При упрощении геометрических соотношений между отклонениями и
и 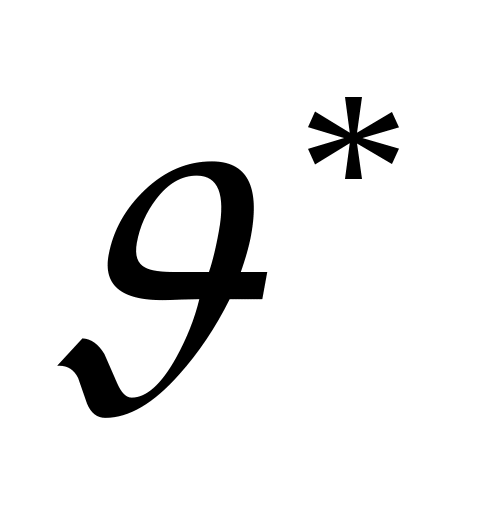 ,
,  и
и 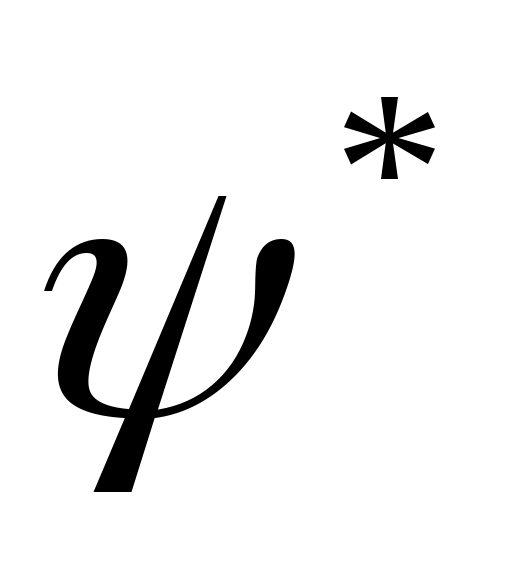 принимаем, что
принимаем, что 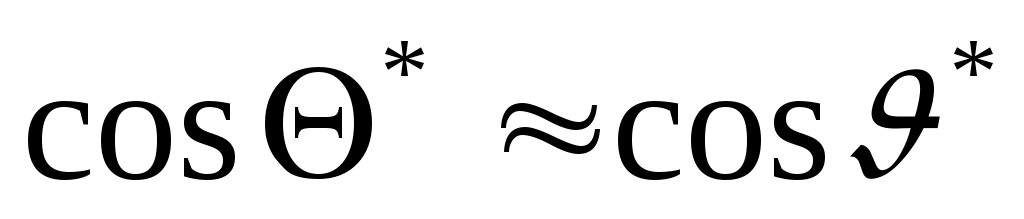 .
.
С учётом этих предположений, а также выражений (17) будем считать, что силы и моменты, входящие в правые части уравнений (1) – (16), зависят от следующих параметров [5]:
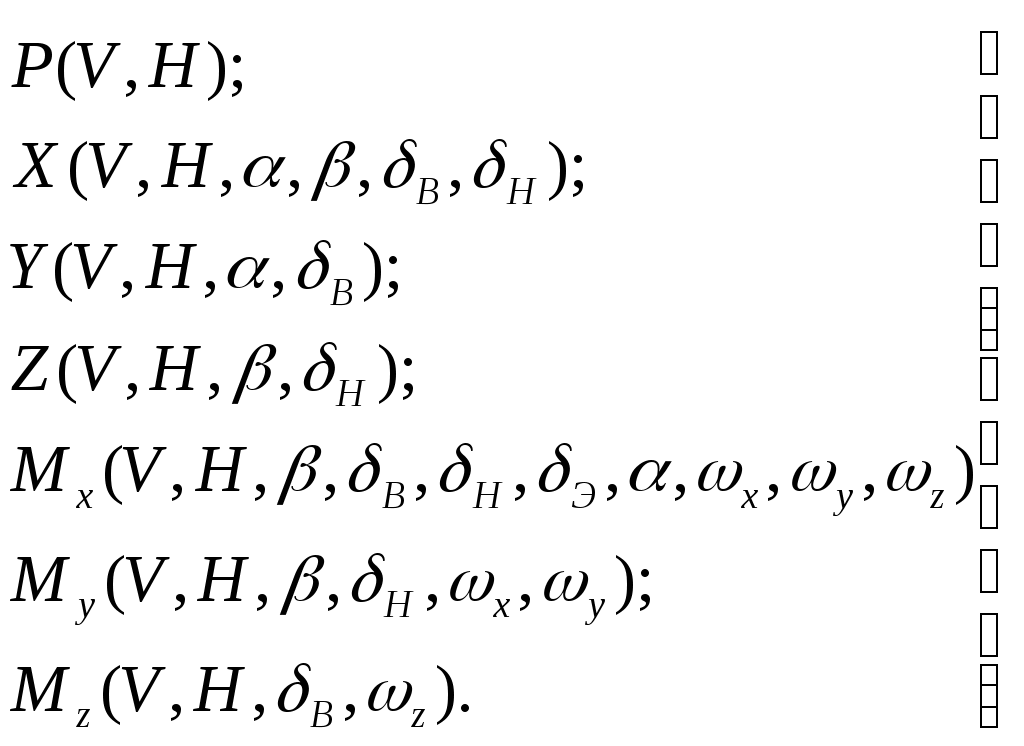 (19)
(19)
Проведем линеаризацию напримере уравнения (1):
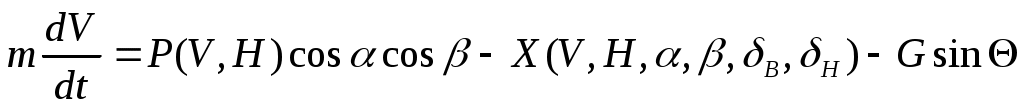 .
.
Придадим параметрам V, H, ,
, 
,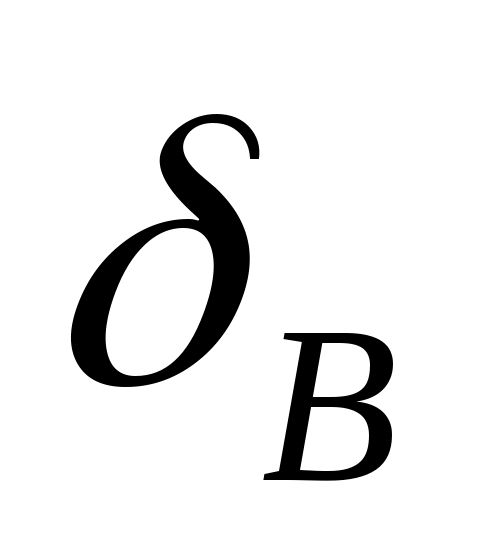 ,
,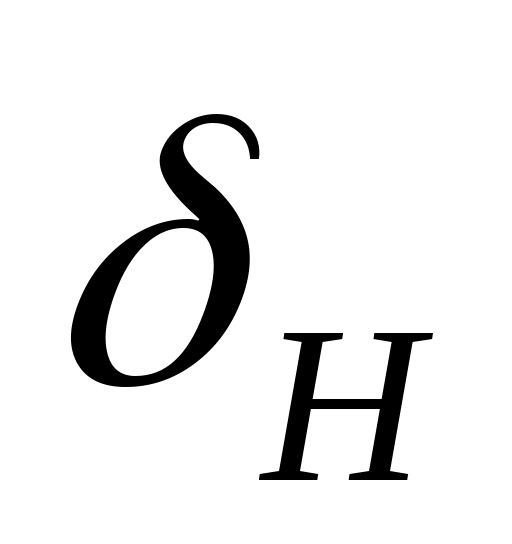 их приращения и введем в уравнение (1) возмущающу силу XB:
их приращения и введем в уравнение (1) возмущающу силу XB:
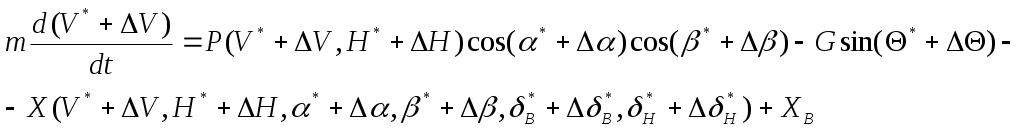
Разложим все функции в последнем уравнении в ряд Тейлора по степеням приращений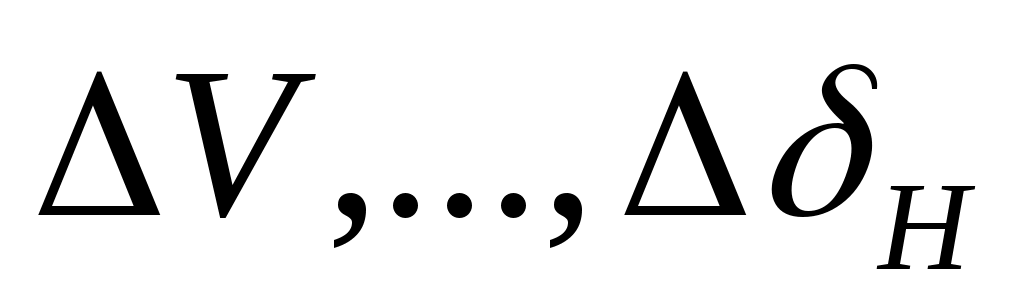 и оставим члены порядка малости не выше первой:
и оставим члены порядка малости не выше первой:
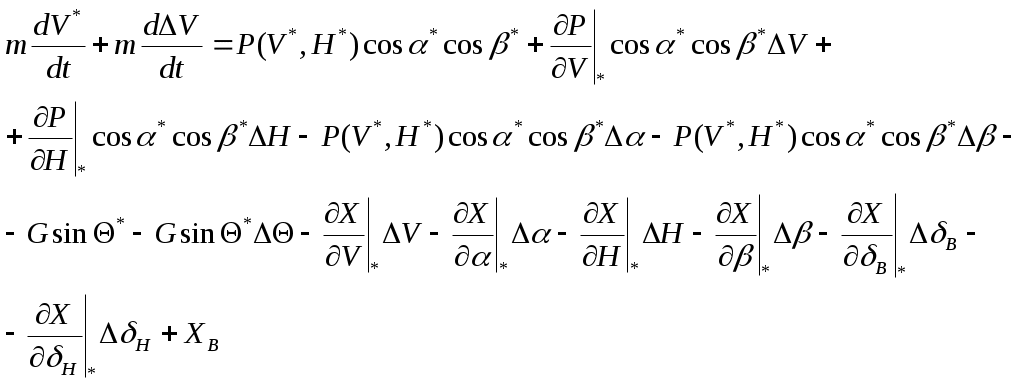
Для невозмущённых слагаемых в левой и правой частях уравнение (1) справедливо как тождество, поэтому линеаризованное уравнение возмущенного движения принимает вид
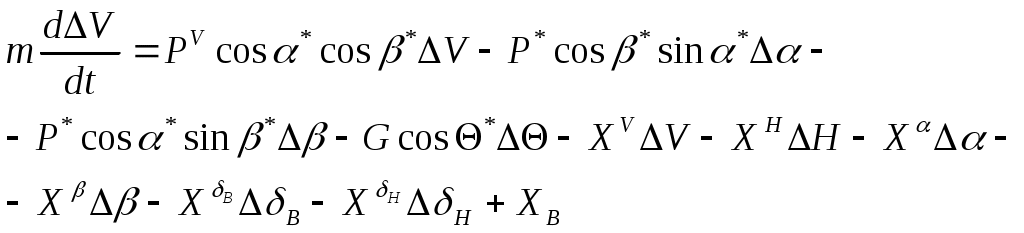
Так как в силу ранее принятых допущений произведения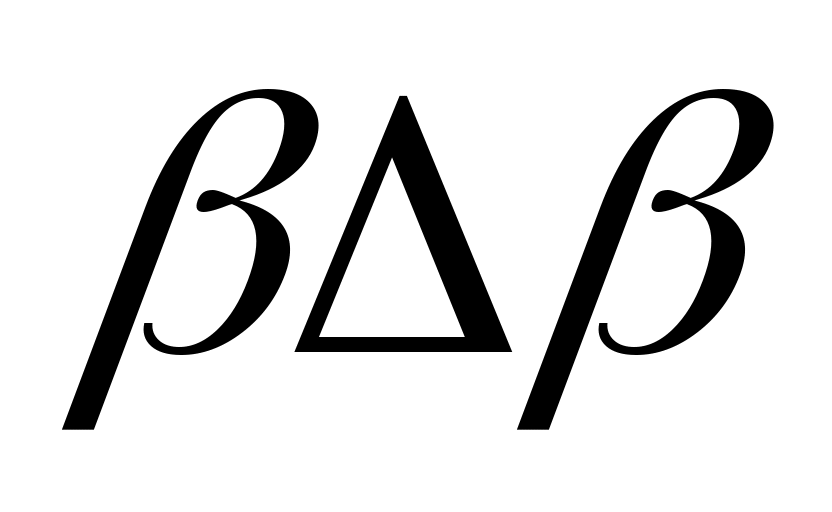 ,
,  ,
, 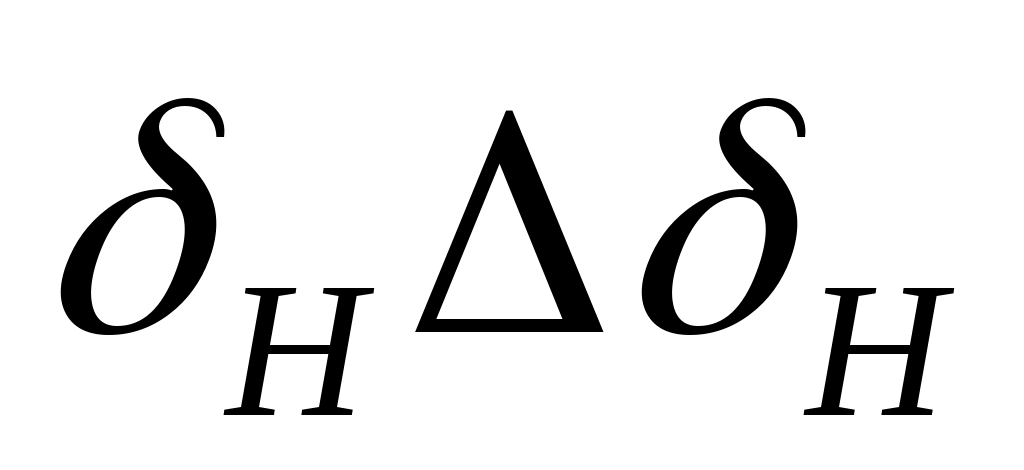 ,
, 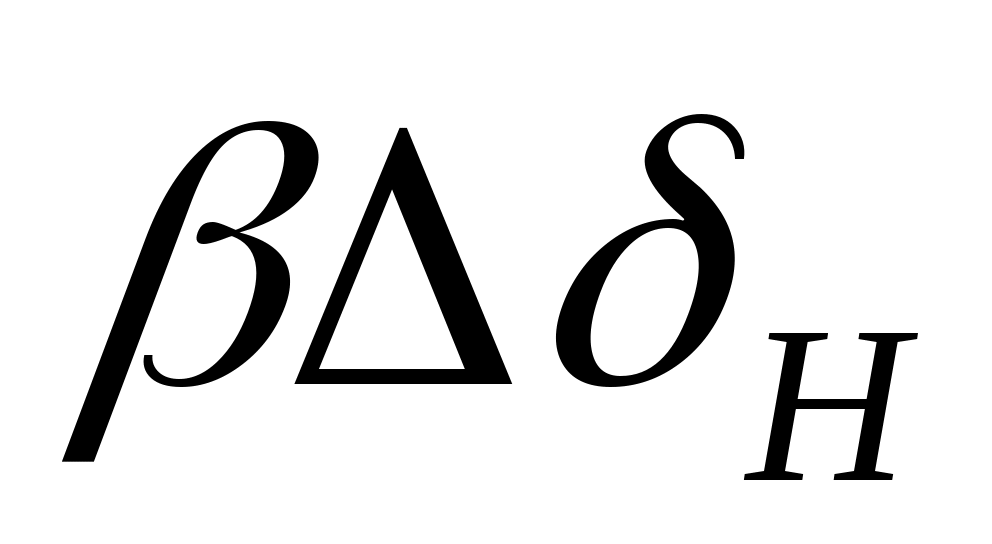 являются величинами второго порядка малости, то из первого уравнения выражения (17) найдём составляющие приращения силы лобового сопротивления
являются величинами второго порядка малости, то из первого уравнения выражения (17) найдём составляющие приращения силы лобового сопротивления
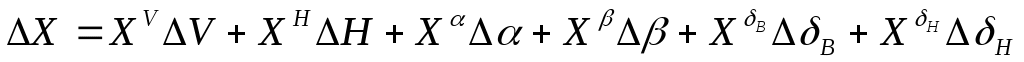 ,
,
Опуская при записи индекс "*":
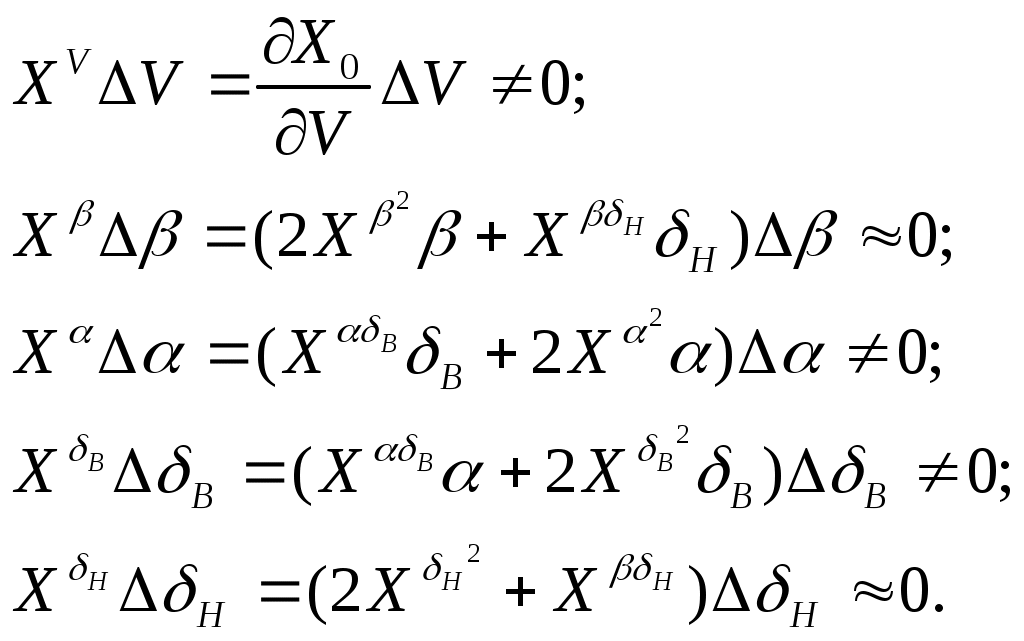
Таким образом, необходимо найти выражения для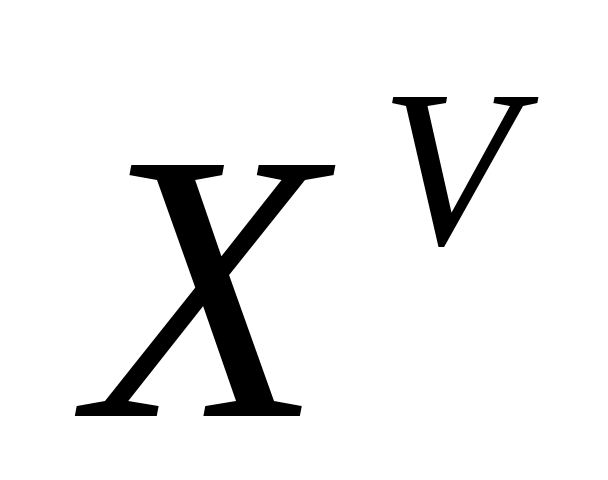 ,
, 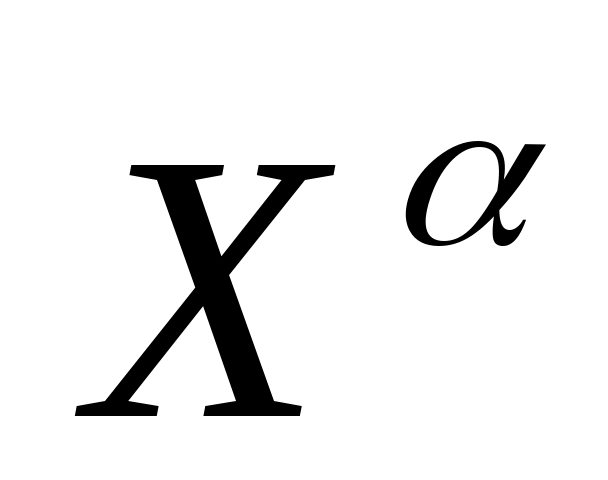 ,
, 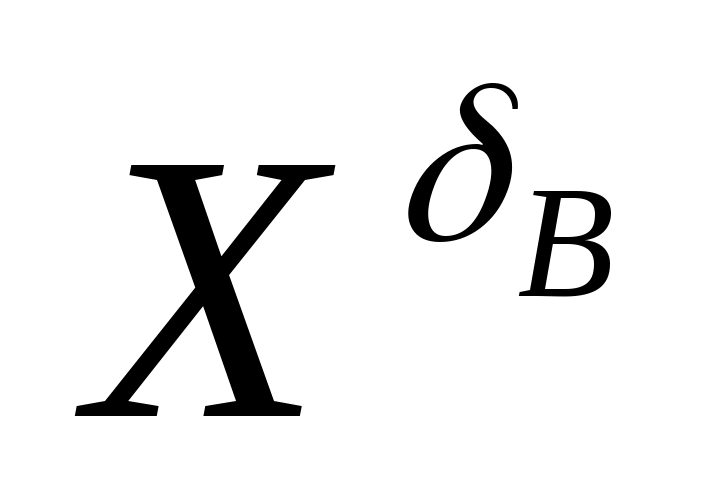 . Для примера найдем развернутое выражение для
. Для примера найдем развернутое выражение для 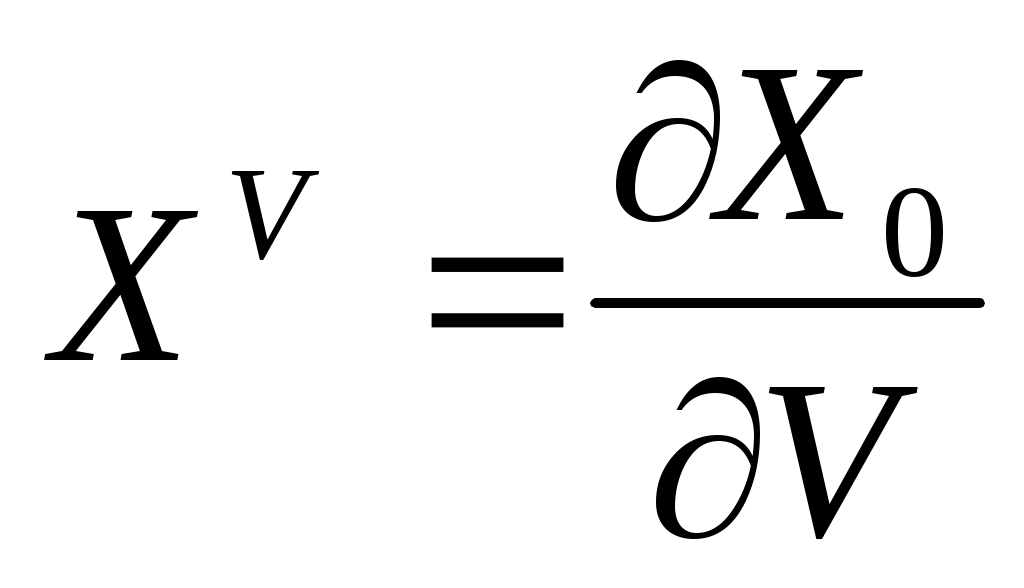 .
.
Известно [5, 4], что
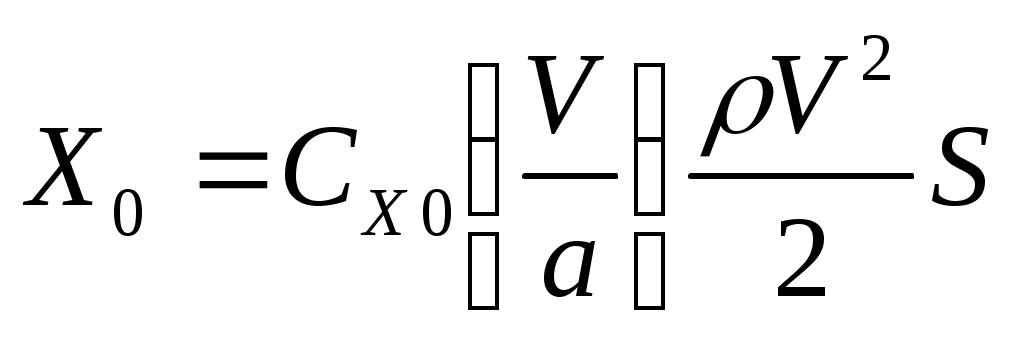 ,
,
a – скорость звука, зависящая от высот полета
;
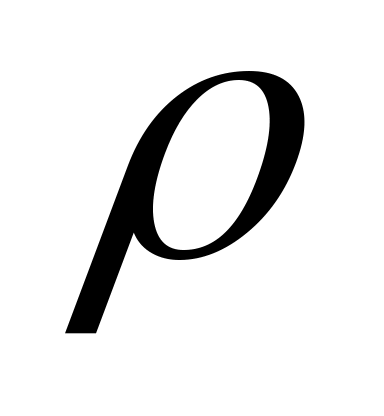 – плотность, также зависящая от высоты:
– плотность, также зависящая от высоты:
S – характерное сечение:
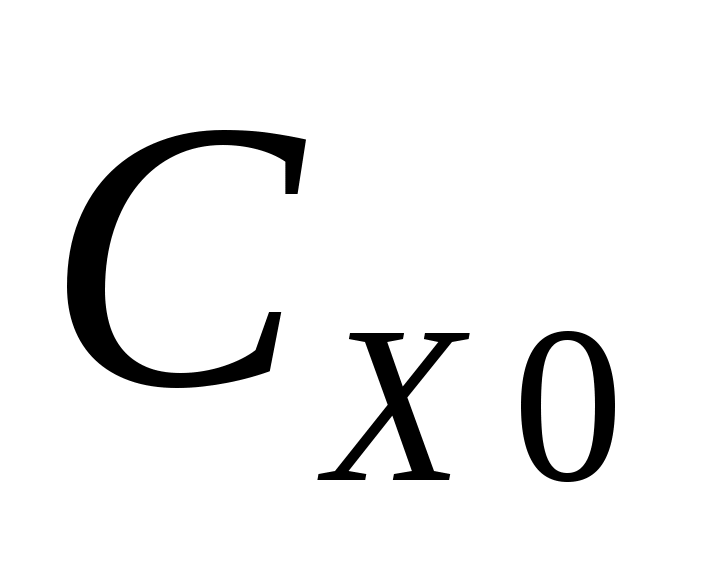 – коэффициент лобового сопротивления, зависящий от числа маха M=V/a.
– коэффициент лобового сопротивления, зависящий от числа маха M=V/a.
В [5, 4] дается физическое толкование и математические выражения для всех аэродинамических сил и моментов. Тогда
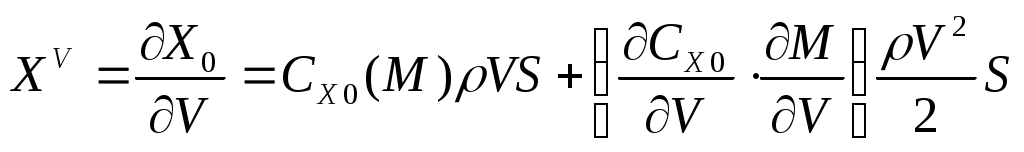 .
.
Обозначив , получим
, получим 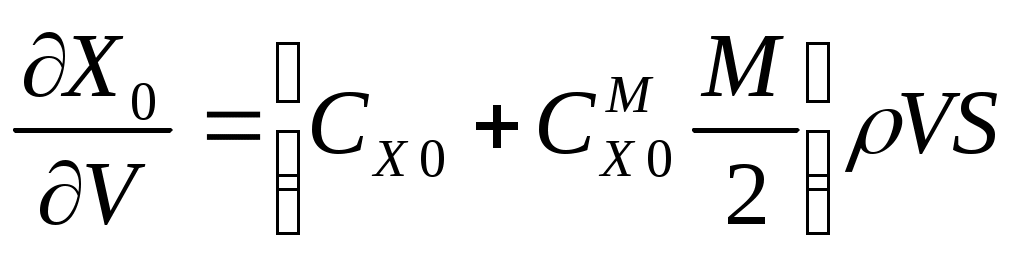 .
.
Коэффициенты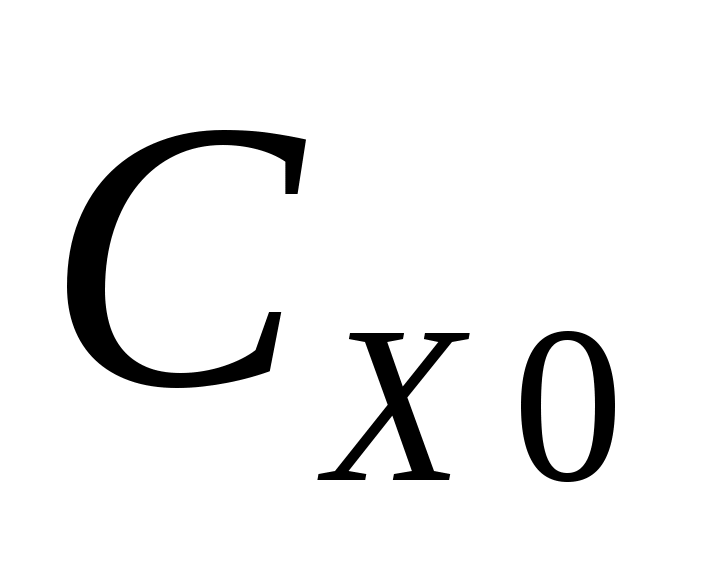 и
и 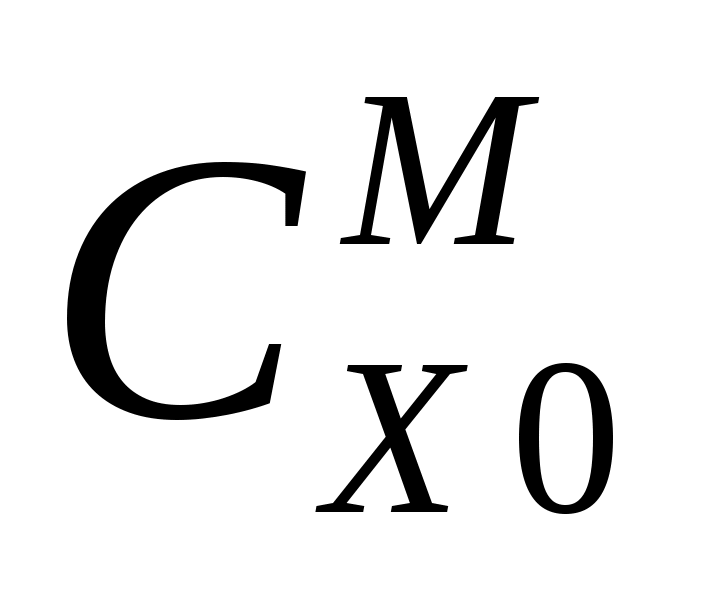 можно вычислить по экспериментальному графику
можно вычислить по экспериментальному графику 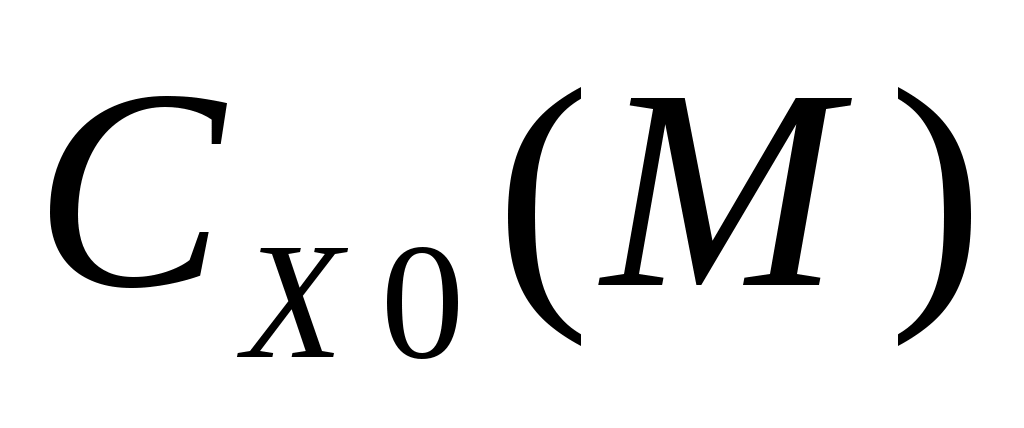 для заданных значений
для заданных значений  и
и 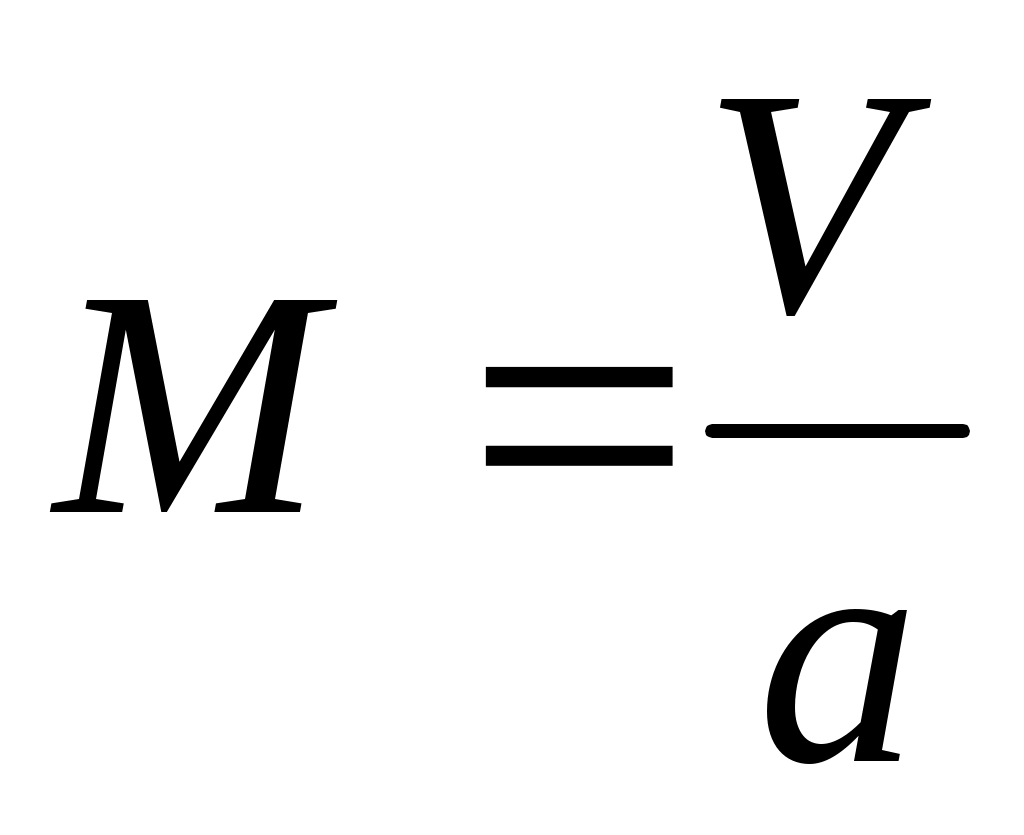 . (Напомним, что в полученных выражениях фигурируют значения параметров невозмущенной траектории.)
. (Напомним, что в полученных выражениях фигурируют значения параметров невозмущенной траектории.)
Аналогично вычисляются и другие производные. Тогда окончательно первое уравнение с ил получим в следующем виде:
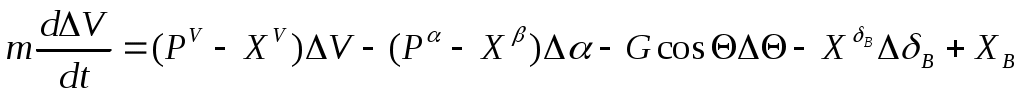 . (1л)
. (1л)
При линеаризации уравнения (2) отбрасывается член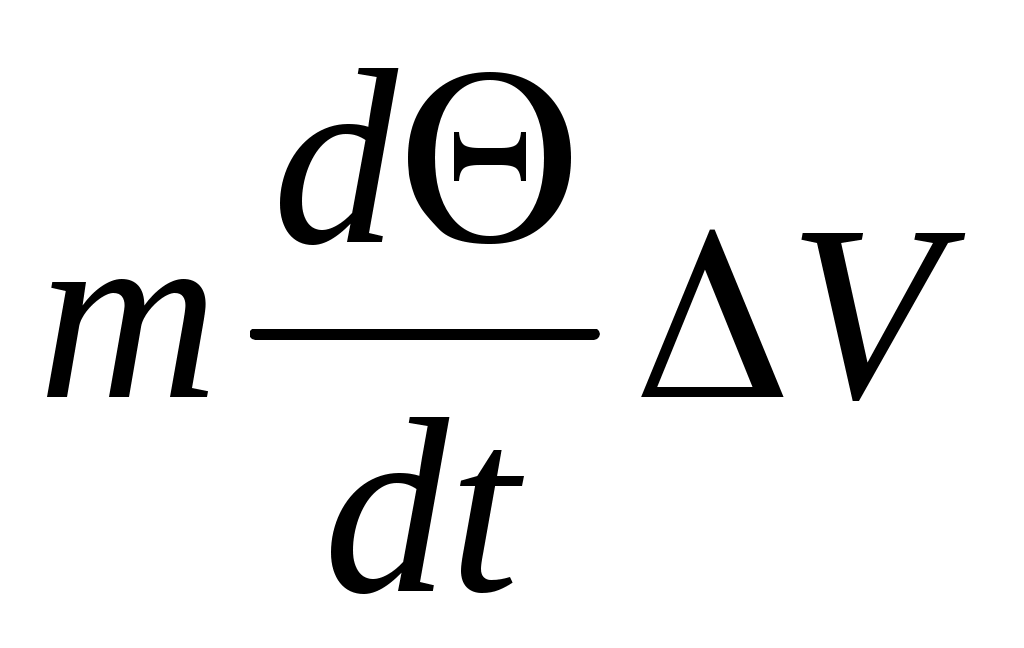 , так как он имеет второй порядок малости согласно допущению, сделанному в § 4 п. 3; второй порядок малости имеют также члены
, так как он имеет второй порядок малости согласно допущению, сделанному в § 4 п. 3; второй порядок малости имеют также члены 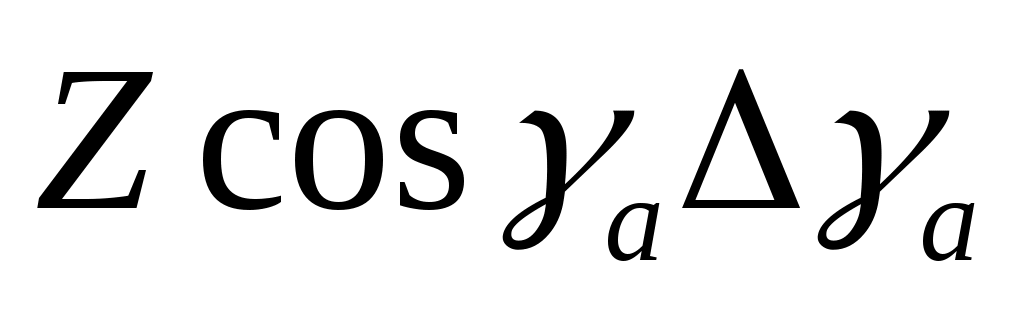 , поскольку
, поскольку 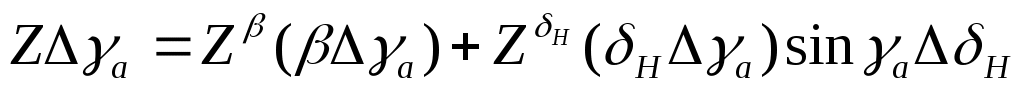 и т. д. Поэтому линеаризованное уравнение (2) имеет следующий вид:
и т. д. Поэтому линеаризованное уравнение (2) имеет следующий вид:
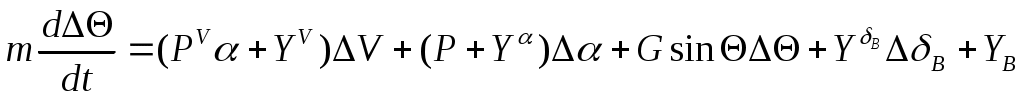 (2л)
(2л)
Уравнение (3) после линеаризации примет такой вид:
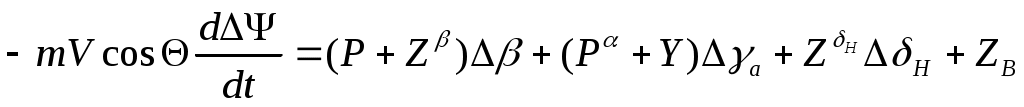 (3л)
(3л)
В этом уравнении отброшены члены
, содержащие произведения малых величин:
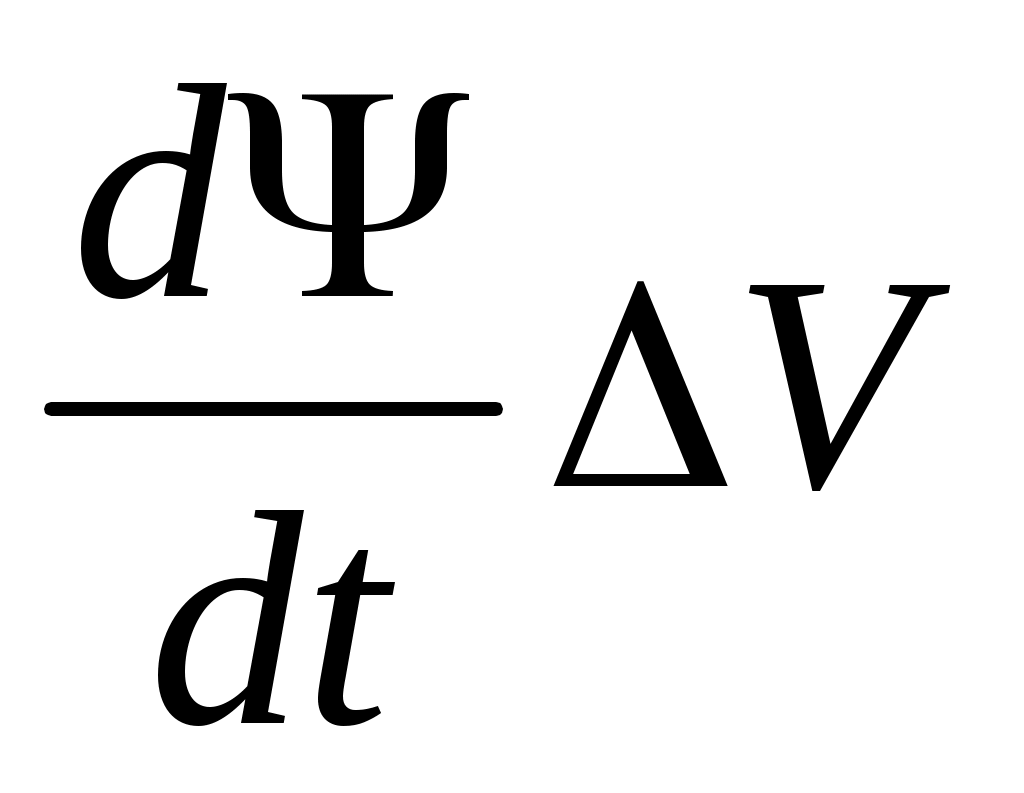 ;
; 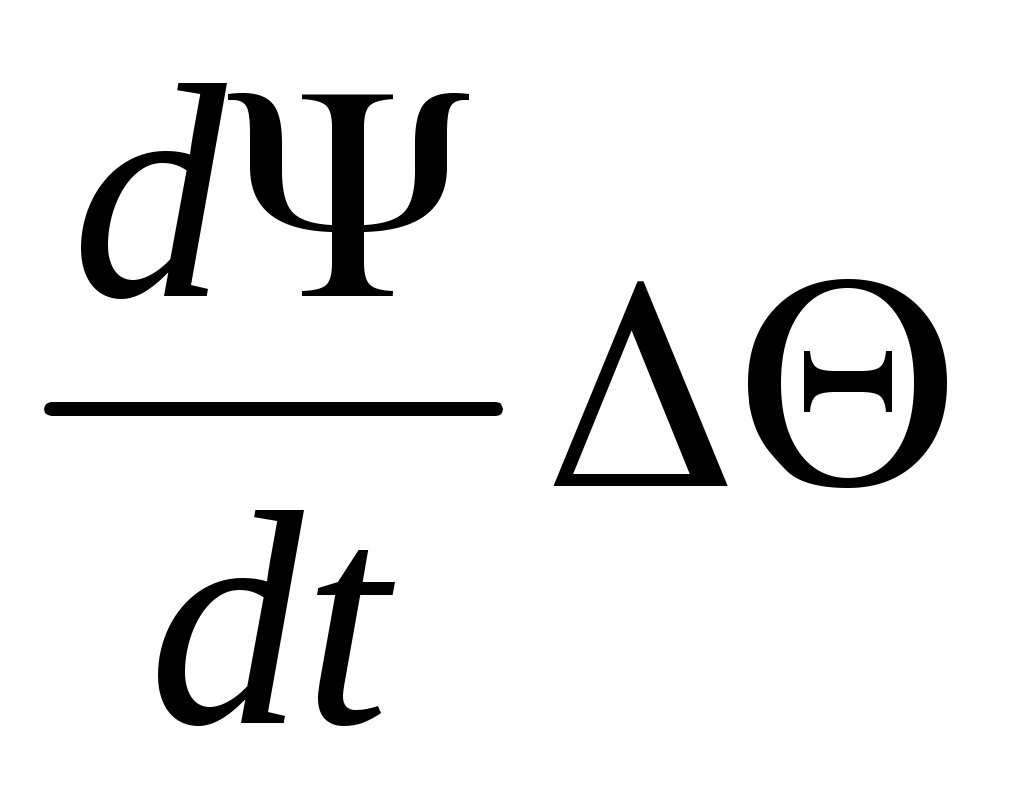 ;
; 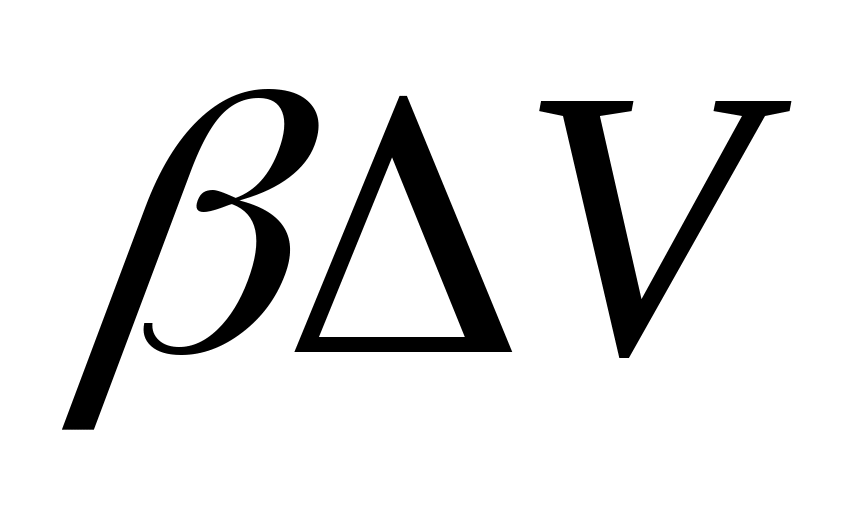 ;
; 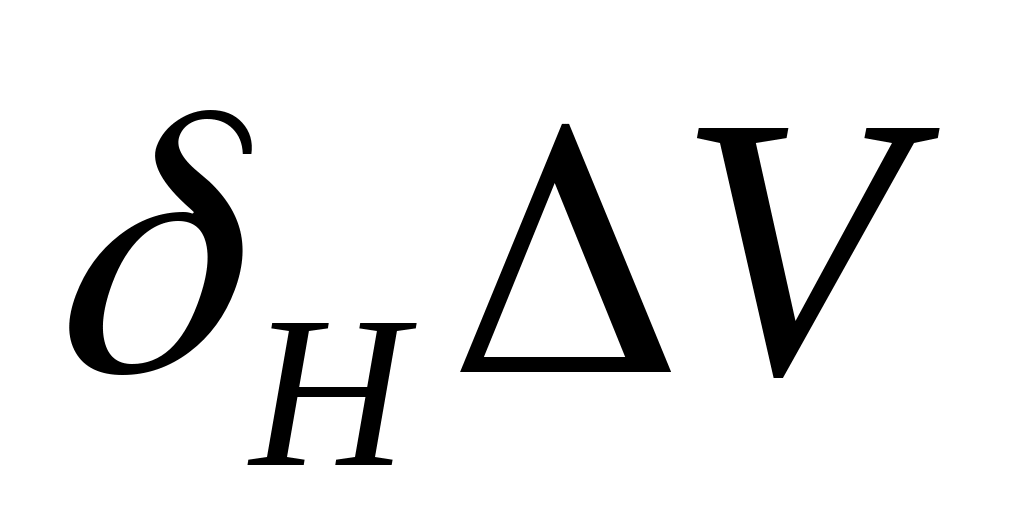 и др.
и др.
Пример линеаризации четвертого уравнения
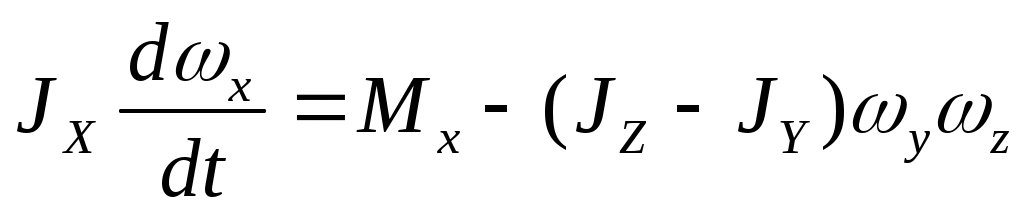 .
.
Уравнение возмущенного движения примет следующий вид:
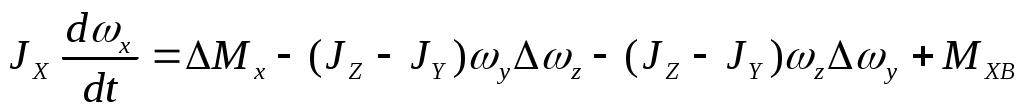 .
.
На основании (19) можно раскрыть вариацию
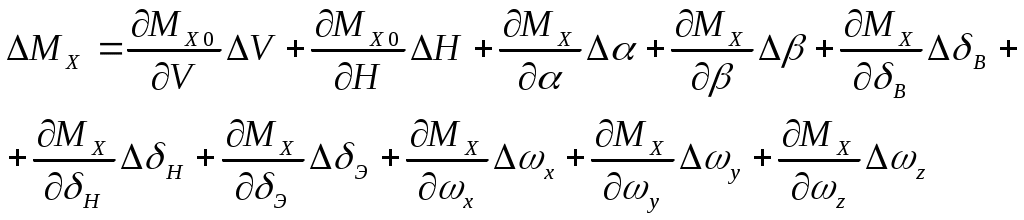
Величины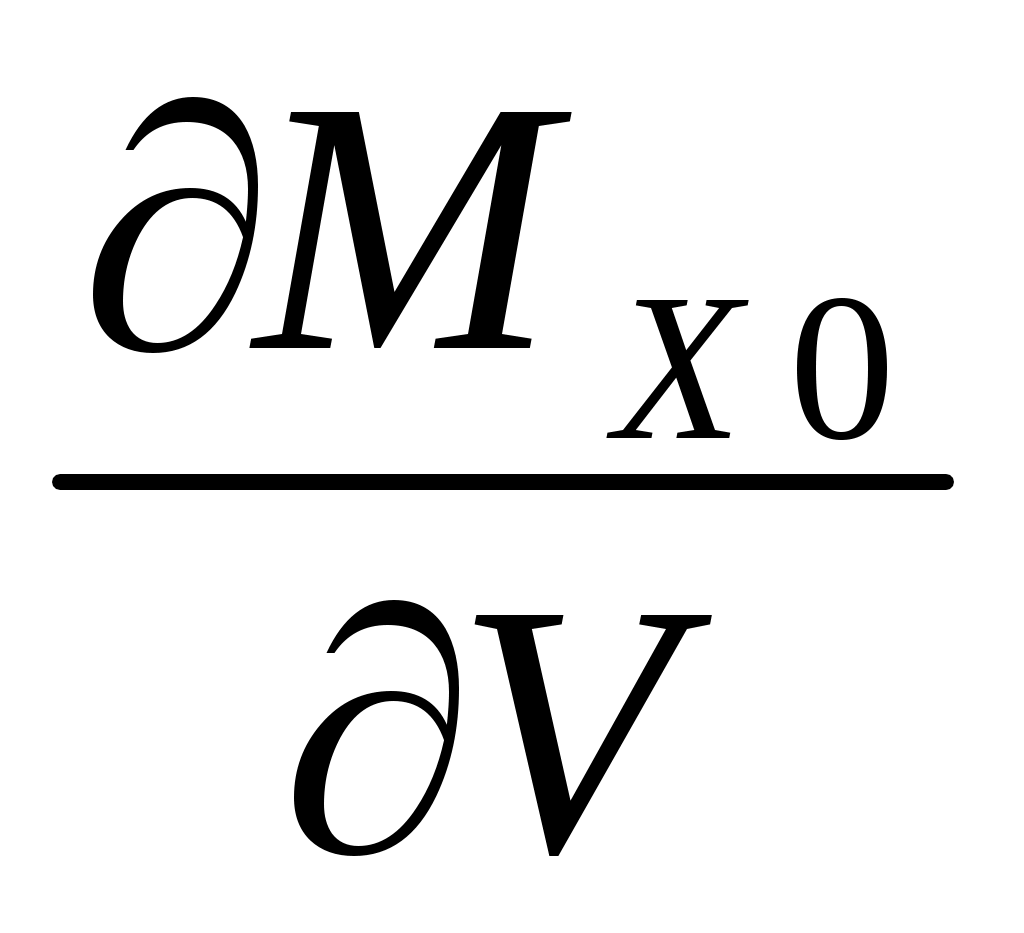 и
и 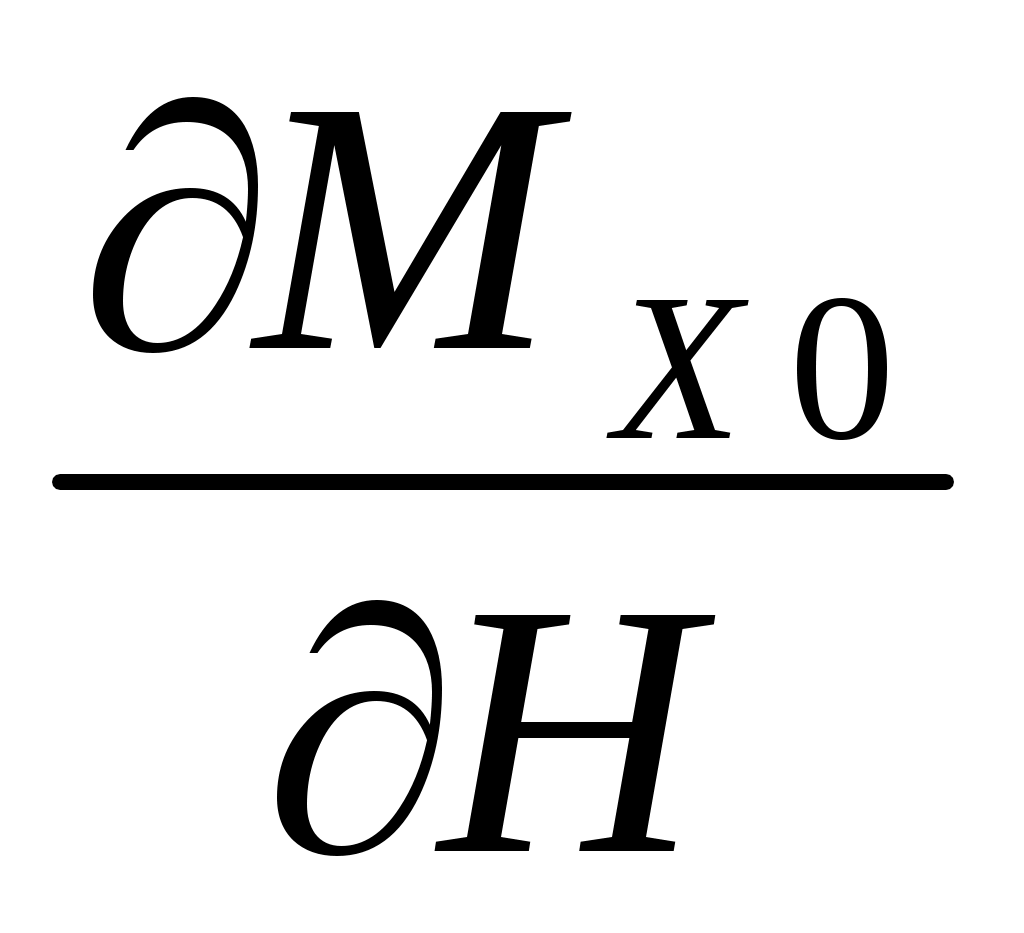 в практических расчетах можно считать малыми, поэтому слагаемые
в практических расчетах можно считать малыми, поэтому слагаемые 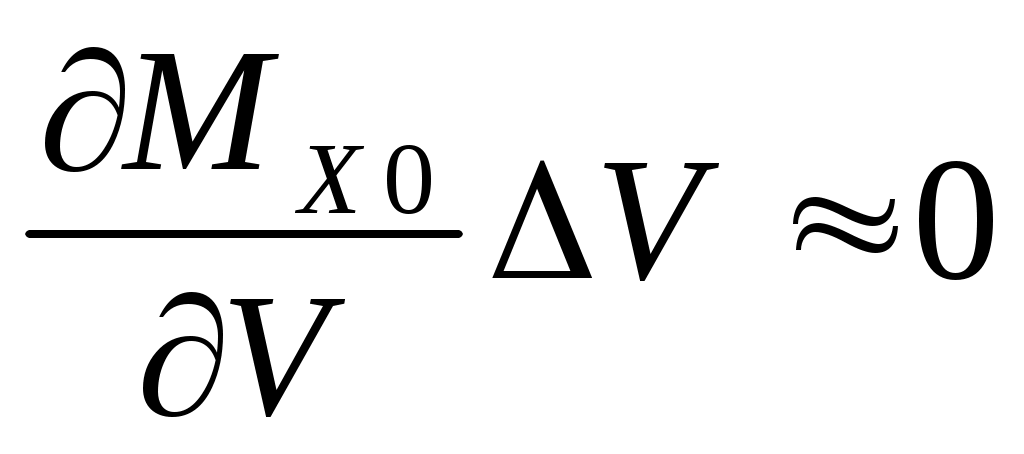 ;
; 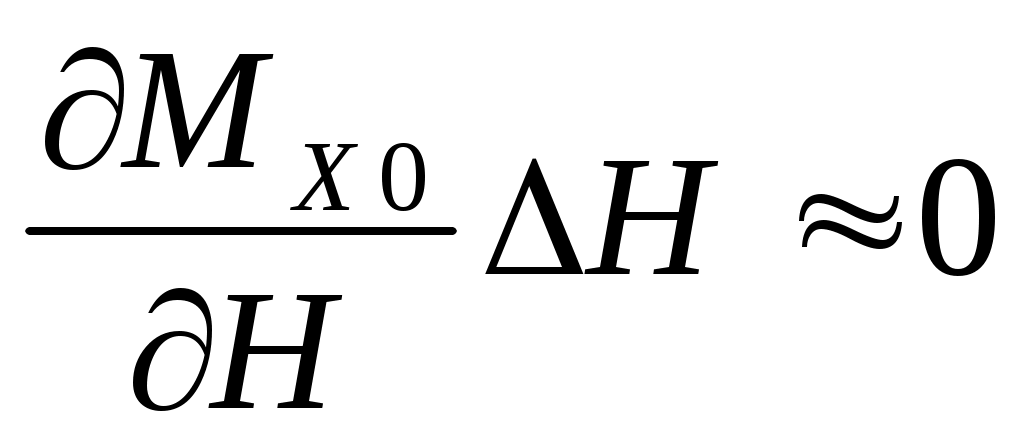 . Мал также значения
. Мал также значения 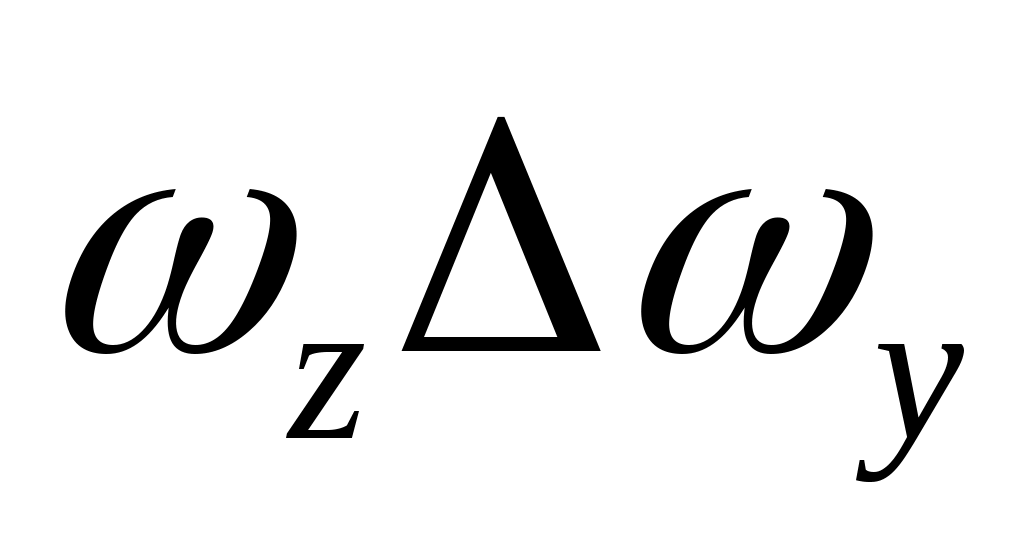 и
и 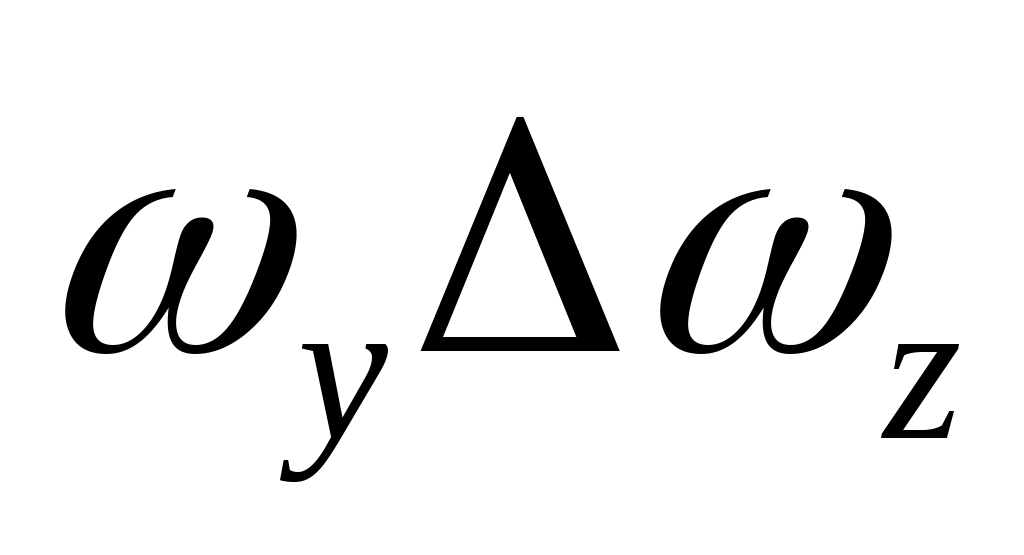 . Учитывая (17) и принятые допущения, сделанные в п.п. 1-4 данного параграфа, вычислим вариации слагаемых
. Учитывая (17) и принятые допущения, сделанные в п.п. 1-4 данного параграфа, вычислим вариации слагаемых 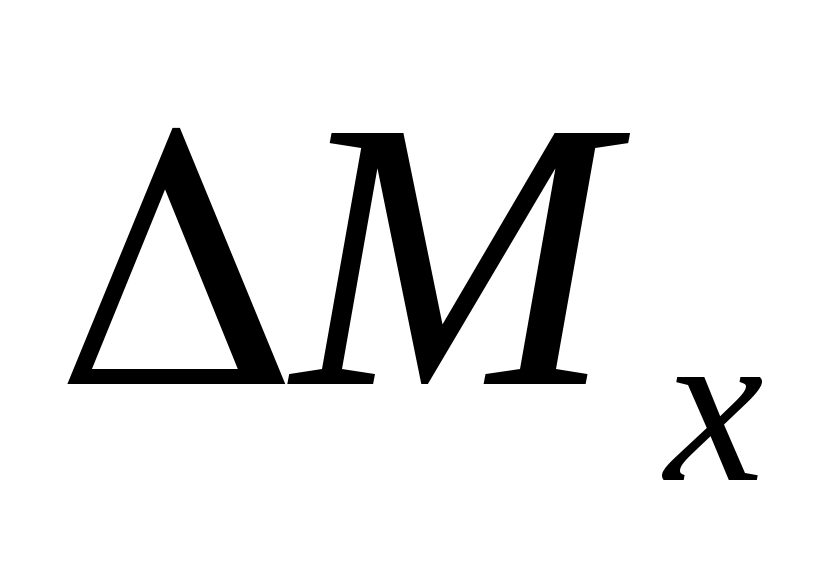 :
:
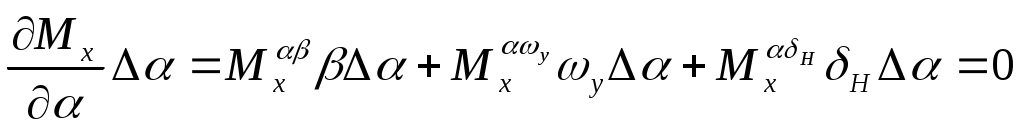 ;
;
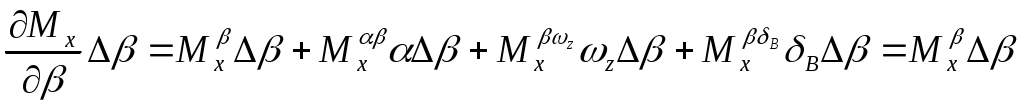 ;
;
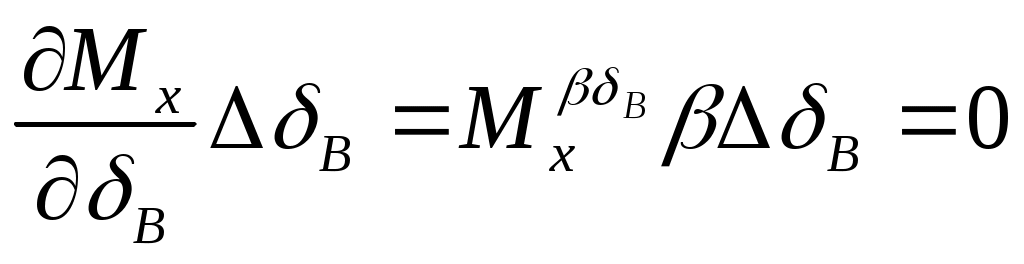 ;
;
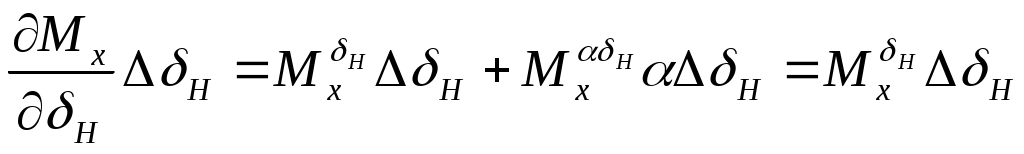 ;
;
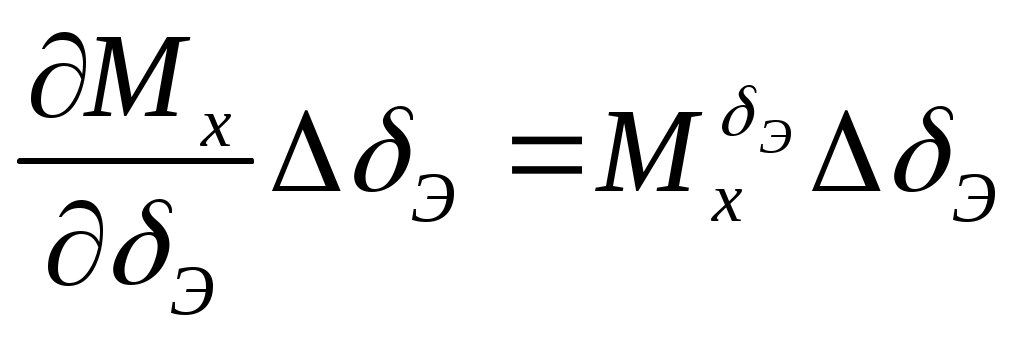 ;
;
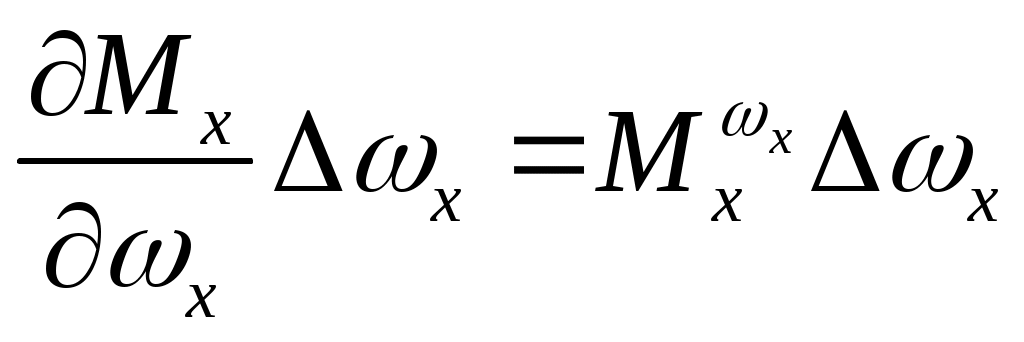 ;
;
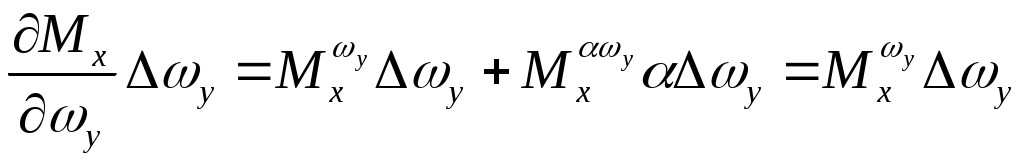 ;
;
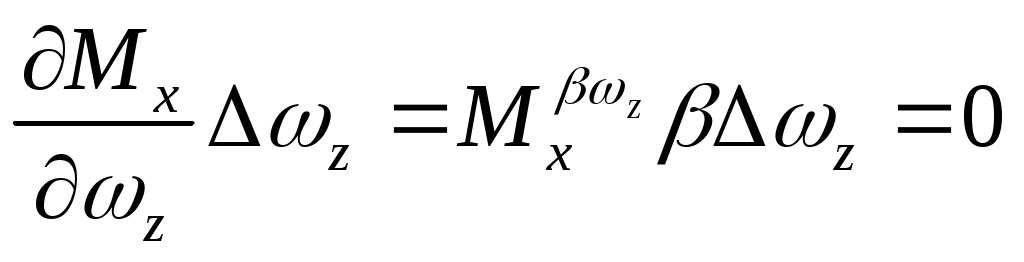 .
.
Запишем линеаризованное уравнение (4):
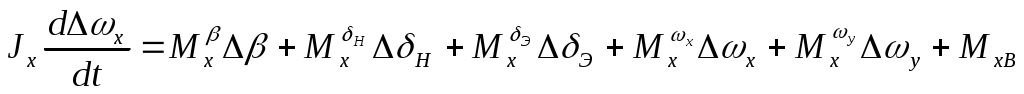 (4л)
(4л)
Аналогично линеаризуем уравнение (5) и (6):
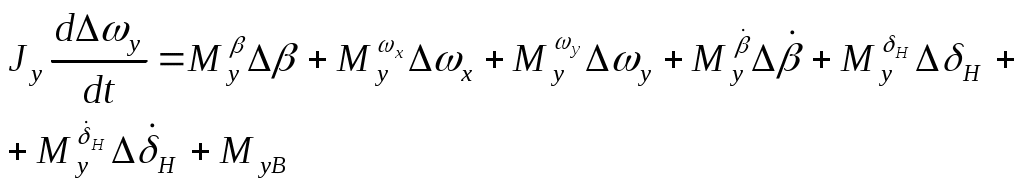 (5л)
(5л)
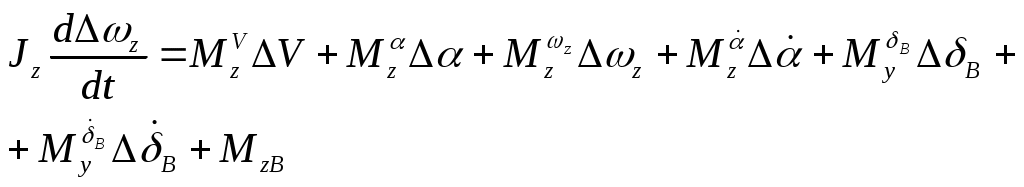 (6л)
(6л)
Разложение в ряд Тейлора уравнений (7), (8), и (9) относительно малых приращений параметров возмущенной траектории дает следующий результат:
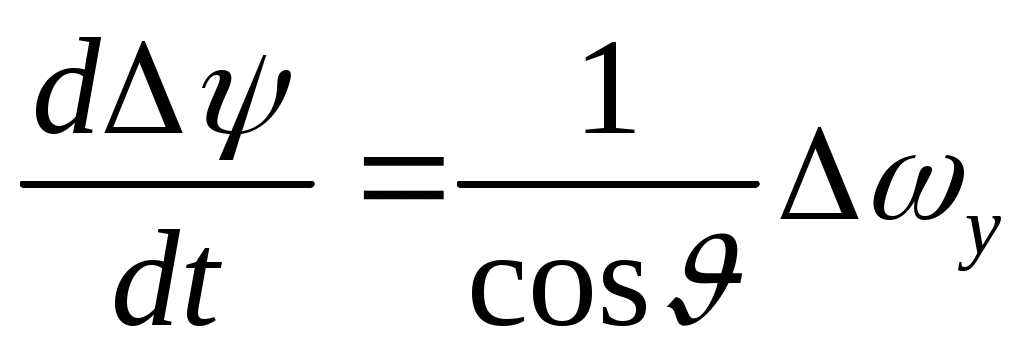 ; (7л)
; (7л)
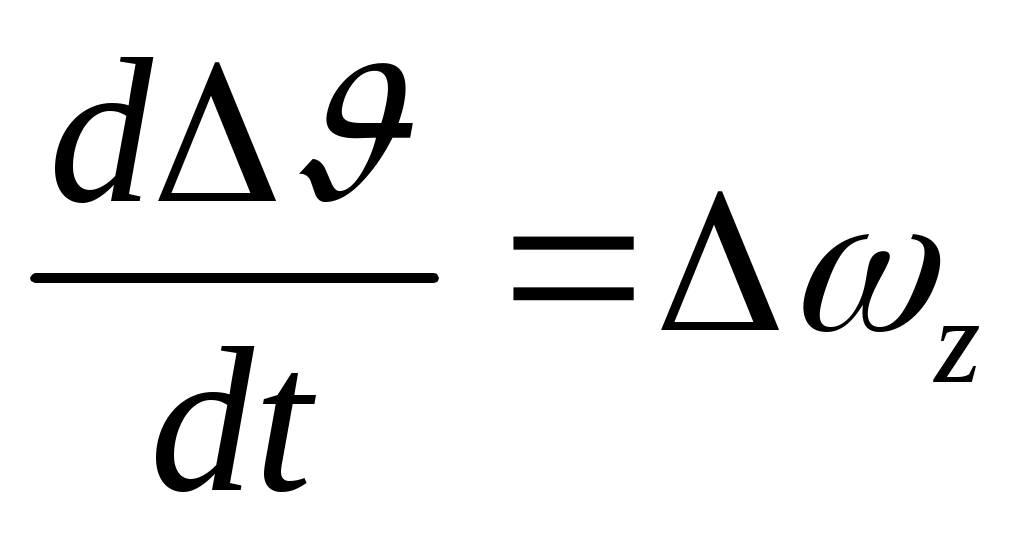 ; (8л)
; (8л)
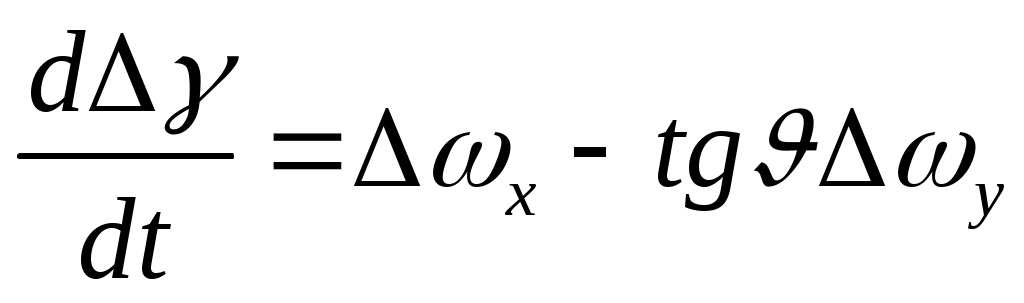 . (9л)
. (9л)
Линеаризуем геометрическое уравнение связи углов (10):
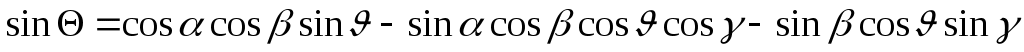 .
.
После разложения в ряд Тейлора данное уравнение дает следующее соотношение между вариациями параметров:
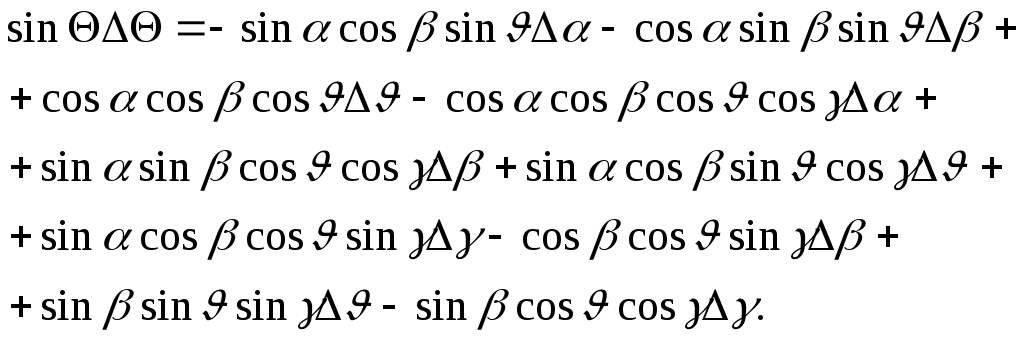
Отсюда с учетом допущений, сделанных в п.п. I – 4 данного параграфа, получаем:
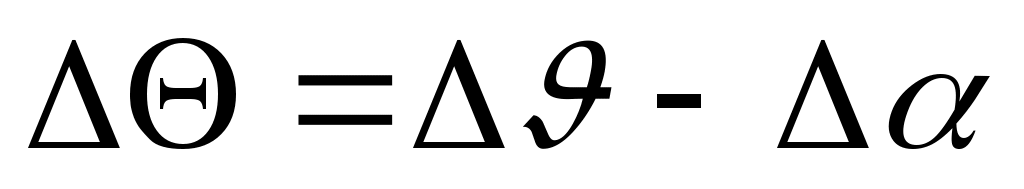 . (10л)
. (10л)
Уравнения (11) и (12) приводятся соответственно к виду
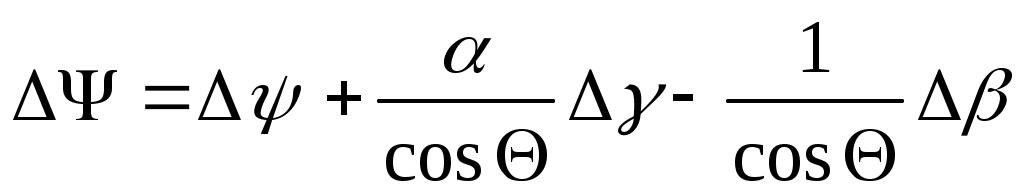 ; (11л)
; (11л)
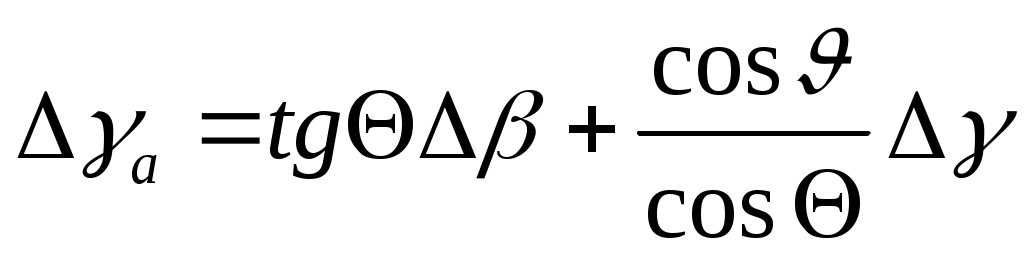 . (12л)
. (12л)
Аналогично получаем линеаризованные кинематические уравнения (13)-(15) движения центра масс ЛА в земной системе координат:
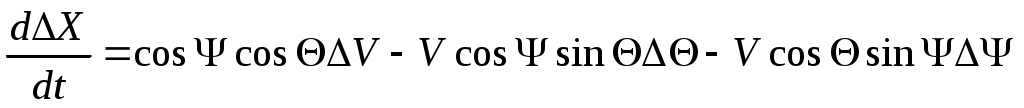 ; (13л)
; (13л)
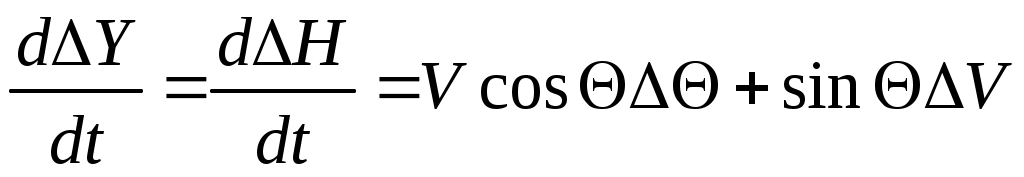 ; (14л)
; (14л)
 ; (15л)
; (15л)
Уравнение (16) – линейно.
Таким образом, получена линеаризованная система дифференциальных уравнений пространственного движения ЛА (1л) – (16л). Анализ динамических свойств ЛА как объекта управления осуществляется в динамике полета на основе именно этих уравнений.
В качестве дальнейших шагов в упрощении линеаризованных уравнений движения ЛА применяют принцип «замороженных коэффициентов», что позволяет свести исходную систему к системе линейных уравнений с постоянными коэффициентами. И, наконец, проводят разделение уравнений движения на три независимые группы, которые
4. При упрощении геометрических соотношений между отклонениями
С учётом этих предположений, а также выражений (17) будем считать, что силы и моменты, входящие в правые части уравнений (1) – (16), зависят от следующих параметров [5]:
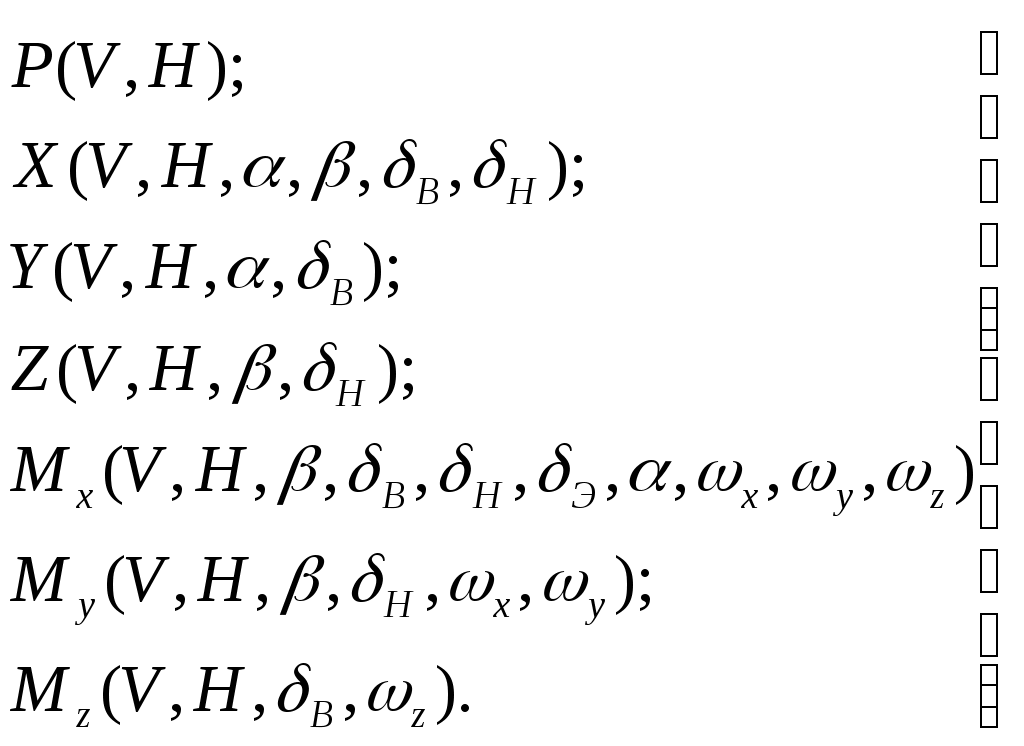 (19)
(19)Проведем линеаризацию напримере уравнения (1):
Придадим параметрам V, H,
,
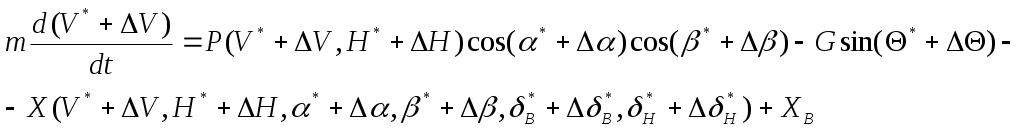
Разложим все функции в последнем уравнении в ряд Тейлора по степеням приращений
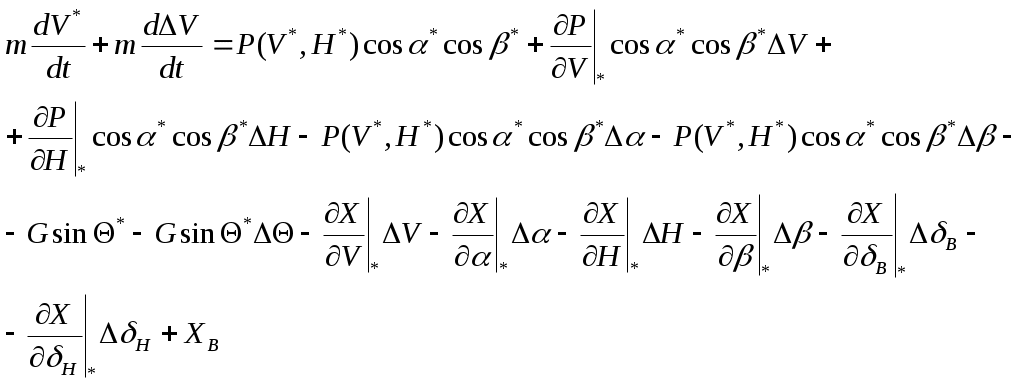
Для невозмущённых слагаемых в левой и правой частях уравнение (1) справедливо как тождество, поэтому линеаризованное уравнение возмущенного движения принимает вид
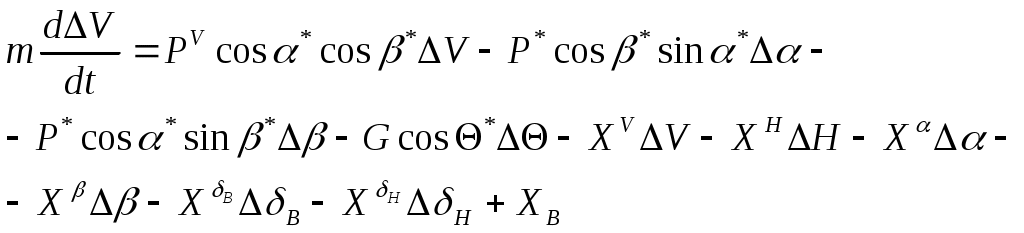
Так как в силу ранее принятых допущений произведения
Опуская при записи индекс "*":
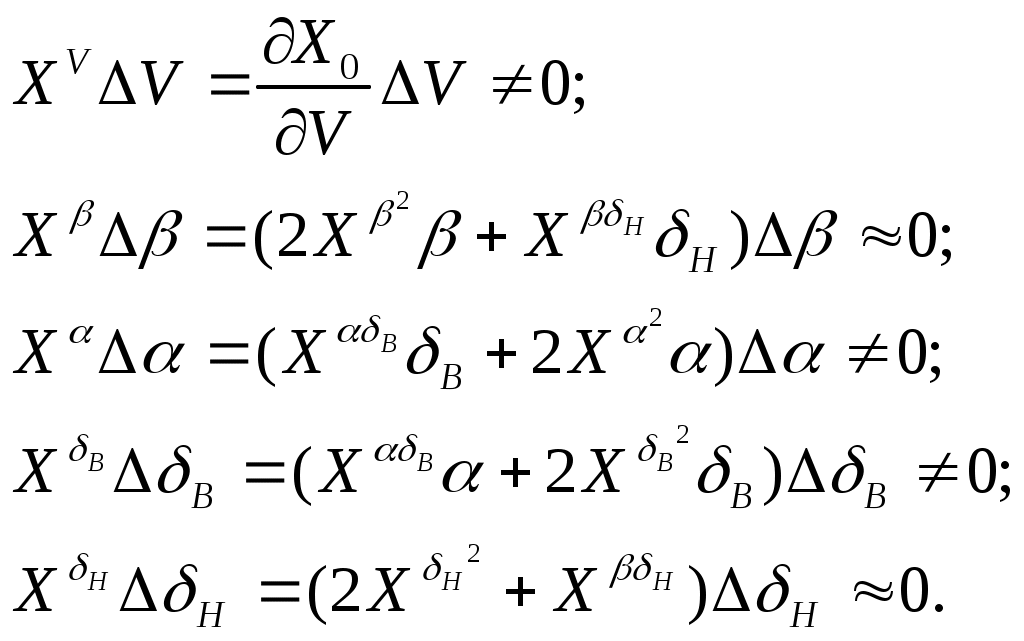
Таким образом, необходимо найти выражения для
Известно [5, 4], что
a – скорость звука, зависящая от высот полета
;
S – характерное сечение:
В [5, 4] дается физическое толкование и математические выражения для всех аэродинамических сил и моментов. Тогда
Обозначив
Коэффициенты
Аналогично вычисляются и другие производные. Тогда окончательно первое уравнение с ил получим в следующем виде:
При линеаризации уравнения (2) отбрасывается член
Уравнение (3) после линеаризации примет такой вид:
В этом уравнении отброшены члены
, содержащие произведения малых величин:
Пример линеаризации четвертого уравнения
Уравнение возмущенного движения примет следующий вид:
На основании (19) можно раскрыть вариацию
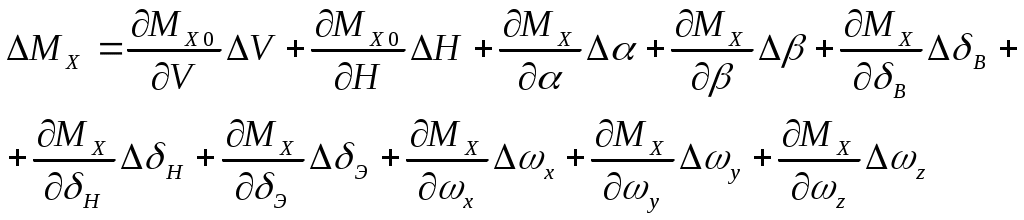
Величины
Запишем линеаризованное уравнение (4):
Аналогично линеаризуем уравнение (5) и (6):
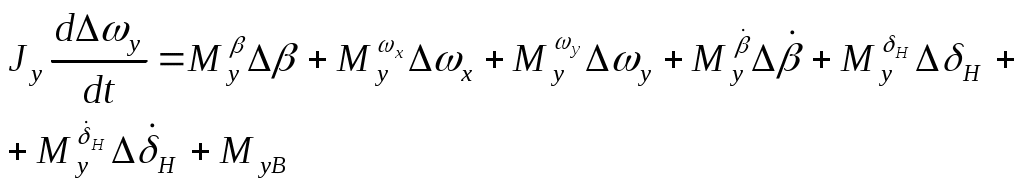 (5л)
(5л)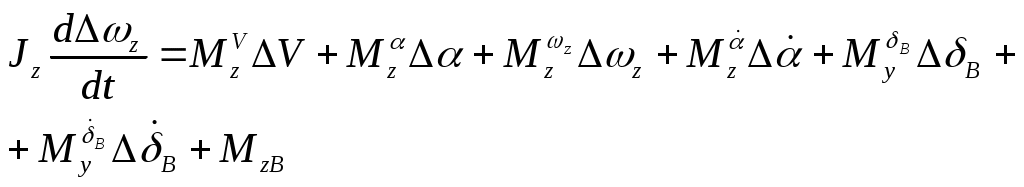 (6л)
(6л)Разложение в ряд Тейлора уравнений (7), (8), и (9) относительно малых приращений параметров возмущенной траектории дает следующий результат:
Линеаризуем геометрическое уравнение связи углов (10):
После разложения в ряд Тейлора данное уравнение дает следующее соотношение между вариациями параметров:
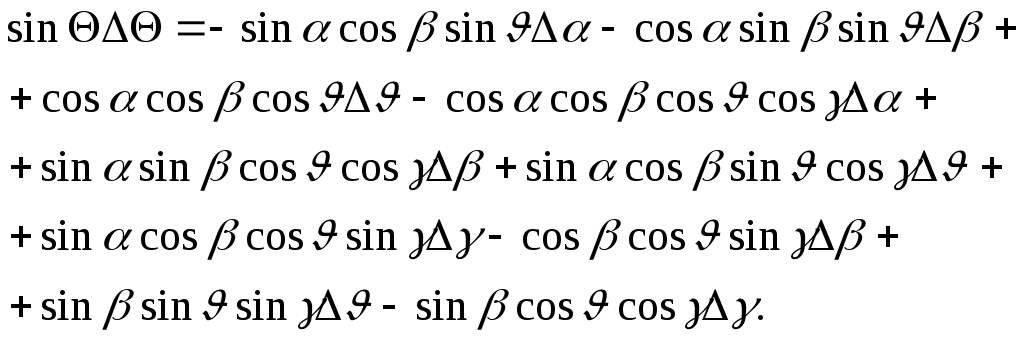
Отсюда с учетом допущений, сделанных в п.п. I – 4 данного параграфа, получаем:
Уравнения (11) и (12) приводятся соответственно к виду
Аналогично получаем линеаризованные кинематические уравнения (13)-(15) движения центра масс ЛА в земной системе координат:
Уравнение (16) – линейно.
Таким образом, получена линеаризованная система дифференциальных уравнений пространственного движения ЛА (1л) – (16л). Анализ динамических свойств ЛА как объекта управления осуществляется в динамике полета на основе именно этих уравнений.
В качестве дальнейших шагов в упрощении линеаризованных уравнений движения ЛА применяют принцип «замороженных коэффициентов», что позволяет свести исходную систему к системе линейных уравнений с постоянными коэффициентами. И, наконец, проводят разделение уравнений движения на три независимые группы, которые