Файл: Методические указания по выполнению рейтинговой работы по дисциплине Теория вероятностей и математическая статистика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 87
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Кафедра математических и естественно-научных дисциплин
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению рейтинговой работы
по дисциплине «Теория вероятностей и математическая статистика»
Уровень высшего образования:
Бакалавриат
Специалитет
Москва 2022
СОДЕРЖАНИЕ
1. ОБЩИЕ ПОЛОЖЕНИЯ 3
Рейтинговая работа по дисциплине выполняется обучающимся в ходе самостоятельной работы и является обязательным элементом балльно-рейтинговой системы (БРС) Университета. 3
1. ОБЩИЕ ПОЛОЖЕНИЯ
Рейтинговая работа по дисциплине выполняется обучающимся в ходе самостоятельной работы и является обязательным элементом балльно-рейтинговой системы (БРС) Университета.
Рейтинговая работа – Расчетно-аналитическое задание.
Расчетно-аналитическое задание – самостоятельная письменная работа, требующая от обучающегося умений применять полученные в ходе изучения дисциплины знания и навыки при решении задач и выполнении заданий по определенной методике, анализировать полученные результаты, обосновывать выводы. Выполнение расчетно-аналитического задания ориентировано на развитие математических способностей, логического и аналитического мышления.
Рейтинговая работа в виде расчетно-аналитического задания состоит из пяти практических заданий. Решение задач расчетно-аналитического задания рассчитано на обретение навыков правильного применения полученных теоретических знаний в конкретных условиях, развитие профессиональных компетенций в целом.
Задание для контрольной работы разработано в десяти вариантах.
Выбор варианта контрольной работы по начальной букве фамилии:
Вариант 1 – «А» - «В»
Вариант 2 – «Г» - «Е»
Вариант 3 – «Ж» - «И»
Вариант 4 – «К» - «Л»
Вариант 5 – «М» - «О»
Вариант 6 – «П» - «С»
Вариант 7 – «Т» - «Ф»
Вариант 8 – «Х» - «Ч»
Вариант 9– «Ш» - «Э»
Вариант 10 – «Ю» - «Я»
2. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ РЕЙТИНГОВОЙ РАБОТЫ
Задание 1. Решить задачи используя основные формулы теории вероятностей.
Вариант 1.
а) Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95; второй сигнализатор срабатывает с вероятностью 0,8. Найти вероятность того, что при аварии сработает только один сигнализатор.
б) В магазин поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20%, второй – 45% и третьей – 35% изделий. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, и для третьей – 4%. Чему равна вероятность того, что оказавшееся нестандартным изделие произведено на ПЕРВОЙ фабрике?
Вариант 2.
а) Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что два из них бракованные?
б) Завод изготовил две партии автомобилей. Первая партия в три раза больше второй. Надежность автомобилей первой партии – 0.9, второй партии – 0.8. Определить вероятность того, что наугад купленный автомобиль будет надежным.
Вариант 3.
а) Найти вероятность того, что среди взятых наудачу пяти деталей две стандартные, если вероятность того, что каждая деталь окажется стандартной, равна 0,9.
б) Предположим, что 5% мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Считая, что мужчин и женщин одинаковое количество, найти вероятность того, что этот человек мужчина.
Вариант 4.
а) В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?
б) На трех станках при одинаковых и независимых условиях изготовляются детали одного наименования. На первом станке изготовляется 10 %, на втором - 30 %, на третьем - 60 % всех деталей. Для каждой детали вероятность быть бездефектной равна 0,7, если она изготовлена на первом станке; 0,8 - если она изготовлена на втором станке; 0,9 - если она изготовлена на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
Вариант 5.
а) В группе студентов, состоящей из 20 человек, 12 юношей и 8 девушек. Для дежурства случайным образом отобрано двое студентов. Какова вероятность того, что среди них будет один юноша и одна девушка?
б) Завод изготовил две партии телевизоров. Первая партия телевизоров в два раза больше второй. Надежность телевизоров первой партии – 0,9, второй партии – 0,8. Определить вероятность того, что наугад купленный телевизор будет надежным.
Вариант 6.
а) В ящике имеется 12 деталей, из которых 5 деталей нестандартны. Сборщик наудачу извлекает из ящика 4 детали. Какова вероятность того, что все они будут нестандартными?
б) На первом заводе из каждых 100 электролампочек производится в среднем 90 стандартных, на втором – 95, на третьем – 85, а продукция этих заводов составляет соответственно 50, 30 и 20% всех электролампочек, поставляемых в магазин. Найти вероятность приобретения в магазине стандартной электролампочки.
Вариант 7.
а) Студент знает 15 из 20 вопросов программы. Какова вероятность того, что он знает все три вопроса, предложенные экзаменатором?
б) Партия деталей изготовлена двумя рабочими. Каждый из них изготовил половину всех деталей. Вероятность брака у них соответственно 0,01 и 0,1. Взятая из партии наугад деталь оказалась бракованной. Какова вероятность того, что ее изготовил второй рабочий?
Вариант 8.
а) Техническое устройство содержит три независимо работающих элемента. Вероятности отказа этих элементов соответственно равны 0,05; 0,07 и 0,09. Найти вероятность того, что техническое устройство не сработает, если для этого достаточно, чтобы отказал хотя бы один элемент.
б) Предположим, что 5% мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Считая, что мужчин и женщин одинаковое количество, найти вероятность того, что этот человек женщина.
Вариант 9.
а) Вероятность попадания в мишень при трех выстрелах хотя бы один раз для некоторого стрелка равна 0,875. Найти вероятность попадания при одном выстреле.
б) 45% телевизоров, имеющихся в магазине, изготовлены на 1-м заводе, 15% - на 2-м заводе, остальные – на 3-м заводе. Вероятности того, что телевизоры, изготовленные на этих заводах, не потребуют ремонта в течение гарантийного срока, равны 0,96, 0,84, 0,9 соответственно. Найти вероятность того, что купленный наудачу телевизор выдержит гарантийный срок работы.
Вариант 10.
а) Исследователь разыскивает нужные ему сведения в трех справочниках. Вероятности того, что эти сведения находятся в первом, во втором и в третьем справочнике равны соответственно 0,7; 0,6; 0,9. Найти вероятность того, что требуемые сведения содержатся хотя бы в одном справочнике.
б) В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили наудачу один шар
, а затем из второй урны вынули наугад один шар. Найти вероятность того, что шар, вынутый из второй урны, окажется черным.
Задание 2. По заданному условию, составить ряд распределения, найти математическое ожидание
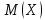 и дисперсию
и дисперсию 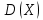 . Номер условия выбирается соответственно варианту.
. Номер условия выбирается соответственно варианту.-
В корзине 10 яблок, причем 6 из них красные. Наудачу выбирают 2 яблока. X число красных яблок, среди отобранных. -
Производится 3 выстрела по мишени, вероятность попадания при каждом выстреле 2/3. X число попаданий в мишень. -
Стрелок стреляет по мишени до первого попадания или пока не израсходует 4 патрона. Вероятность попадания при одном выстреле равна 0,7. X число израсходованных патронов. -
В ралли участвуют 4 машины. Вероятность выхода из соревнований в результате поломки для каждой машины равна 1/5. X число машин, вышедших из соревнования. -
4 лодки пересекают озеро на перегонки, вероятность того, что одна из лодок может отстать, для каждой считается равной 0,1. X число отставших лодок. -
Из колоды карт выбирают 4 карты. X число пиковых карт среди отобранных. -
3 кольца бросается на колышек до первого попадания. Вероятность попадания при каждом броске равна 0,4. X число промахов. -
X число появлений герба при четырех подбрасываниях монеты. -
На складе имеется 5 принтеров, 3 из них изготовлены фирмой HP. Наудачу взято 2 принтера. X число взятых принтеров, изготовленных фирмой HP. -
Вероятность того, что лампа останется исправной равна 0,7. В коридоре поставили 3 новых лампы. X число ламп, оставшихся исправными.
Задание 3. Непрерывная случайная величина задана плотностью вероятности. Найти: 1) коэффициент C; 2) построить график плотности распределения; 3) вычислить математическое ожидание
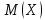 . Функция плотности выбирается из таблицы по номеру согласно варианту.
. Функция плотности выбирается из таблицы по номеру согласно варианту.| 1. 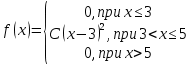 | 2. 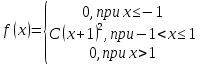 |
| 3. 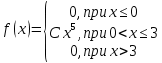 | 4. 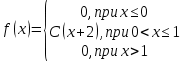 |
| 5. 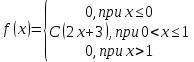 | 6. 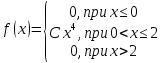 |
| 7. 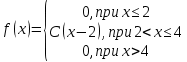 | 8. 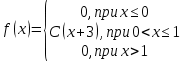 |
| 9. 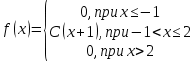 | 10. 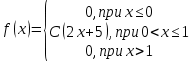 |
Задание 4. Случайная величина X имеет нормальное распределение, известно a и
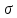 . Записать плотность распределения и построить её график; найти вероятность попадания в заданный интервал и соответствующую область под графиком заштриховать. Данные по коэффициентам a и
. Записать плотность распределения и построить её график; найти вероятность попадания в заданный интервал и соответствующую область под графиком заштриховать. Данные по коэффициентам a и 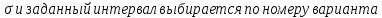 .
.| № варианта | a | 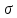 | интервал |
| 1. | -30 | 5 | 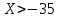 |
| 2. | 20 | 10 | 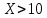 |
| 3. | -1 | 1 | 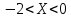 |
| 4. | -4 | 2 | 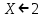 |
| 5. | -7 | 3 | 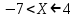 |
| 6. | -3 | 6 | 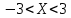 |
| 7. | 10 | 10 | 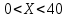 |
| 8. | -20 | 20 | 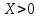 |
| 9. | 0 | 2 | 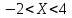 |
| 10. | -10 | 5 | 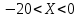 |
Задание 5. По результатам обследования выборки записать ранжированный ряд и определить выборочную среднюю и величину