Файл: Вариант 8 Решите задачу графическим методом. Найти максимум и минимум функции при ограничениях Решение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 60
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
записываем наименьшее из значений 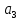 и
и 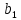
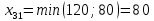 и исключаем из дальнейшего рассмотрения
и исключаем из дальнейшего рассмотрения 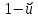 столбец. Запасы третьего поставщика уменьшаются на величину
столбец. Запасы третьего поставщика уменьшаются на величину 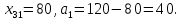
С оставшейся матрицей поступаем аналогично предыдущему:
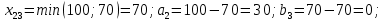
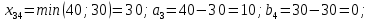
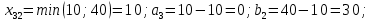
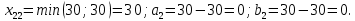
Построенный начальный план перевозок является невырожденным, так как число назначенных перевозок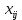 равно
равно 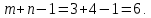
Определим полную стоимость перевозок по найденному опорному плану:
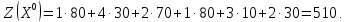
Проверим план, построенный методом «минимальной стоимости» на оптимальность. С помощью метода потенциалов вычислим потенциалы строк и столбцов по стоимости перевозок в загруженных клетках. Если известен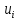 , то
, то 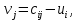 если известен
если известен 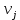 , то
, то 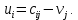 Положим, например,
Положим, например, 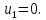 Тогда будут вычислены и остальные потенциалы строк и столбцов.
Тогда будут вычислены и остальные потенциалы строк и столбцов.
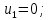
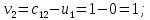
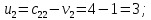
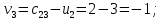
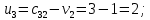
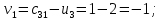
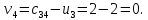
Для незагруженных клеток вычислим величины превышения стоимости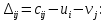
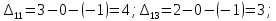
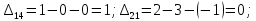
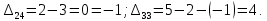
Полученный план не оптимален. Среди оценок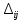 имеется отрицательное значение. Потенциальной является клетка
имеется отрицательное значение. Потенциальной является клетка 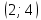 . От клетки
. От клетки 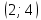 строим замкнутый контур:
строим замкнутый контур: 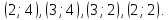 Начиная с клетки
Начиная с клетки 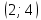 разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки
разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки 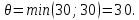 Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Определим полную стоимость перевозок по найденному опорному плану:
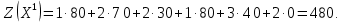
Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:
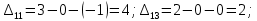
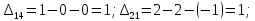
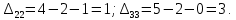
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален.
Ответ: оптимальный план перевозок, обеспечивающий минимальные затраты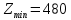 (усл.ед.):
(усл.ед.):
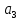 и
и 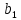
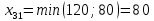 и исключаем из дальнейшего рассмотрения
и исключаем из дальнейшего рассмотрения 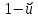 столбец. Запасы третьего поставщика уменьшаются на величину
столбец. Запасы третьего поставщика уменьшаются на величину 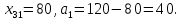
С оставшейся матрицей поступаем аналогично предыдущему:
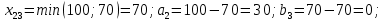
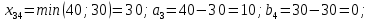
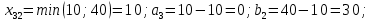
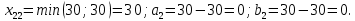
| Поставщики | Потребители | Мощности поставщиков | |||
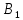 | 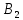 | 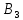 | 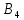 | ||
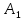 | 3 | 1 80 | 2 | 1 | 80 |
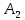 | 2 | 4 30 | 2 70 | 2 | 100 |
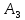 | 1 80 | 3 10 | 5 | 2 30 | 120 |
| Мощности потребителей | 80 | 120 | 70 | 30 | 300 |
Построенный начальный план перевозок является невырожденным, так как число назначенных перевозок
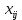 равно
равно 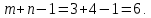
Определим полную стоимость перевозок по найденному опорному плану:
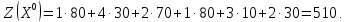
Проверим план, построенный методом «минимальной стоимости» на оптимальность. С помощью метода потенциалов вычислим потенциалы строк и столбцов по стоимости перевозок в загруженных клетках. Если известен
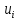 , то
, то 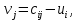 если известен
если известен 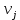 , то
, то 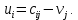 Положим, например,
Положим, например, 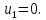 Тогда будут вычислены и остальные потенциалы строк и столбцов.
Тогда будут вычислены и остальные потенциалы строк и столбцов.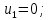
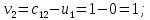
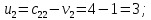
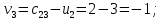
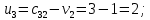
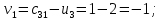
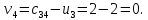
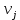 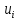 | 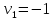 | 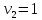 | 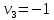 | 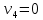 |
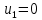 | 3 | 1 80 | 2 | 1 |
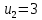 | 2 |  - 4 - 430 | 2 70 | + 2 |
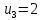 | 1 80 | + 3 10 | 5 | - 2 30 |
Для незагруженных клеток вычислим величины превышения стоимости
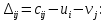
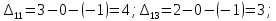
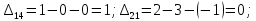
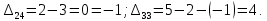
Полученный план не оптимален. Среди оценок
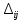 имеется отрицательное значение. Потенциальной является клетка
имеется отрицательное значение. Потенциальной является клетка 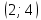 . От клетки
. От клетки 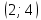 строим замкнутый контур:
строим замкнутый контур: 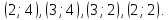 Начиная с клетки
Начиная с клетки 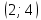 разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки
разметим вершины контура попеременно знаками плюс «+», минус «-», обходя замкнутый контур в любом направлении. Из клеток, помеченных знаком «-», выбираем наименьшее значение объема перевозки 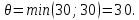 Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».
Сформируем новый улучшенный план: на 30 увеличим перевозки в клетках, помеченных знаком «+», и уменьшим в клетках, помеченных знаком «-».   |  |  | 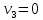 |  |
 | 3 | 1 80 | 2 | 1 |
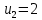 | 2 | 4 | 2 70 | 2 30 |
 | 1 80 | 3 40 | 5 | 2 0 |
Определим полную стоимость перевозок по найденному опорному плану:
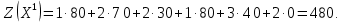
Вычислим потенциалы и величины превышения стоимости для незагруженных клеток:
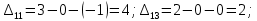
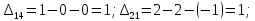
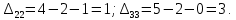
Характеристики свободных клеток не отрицательны, следовательно, текущий план оптимален.
Ответ: оптимальный план перевозок, обеспечивающий минимальные затраты
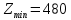 (усл.ед.):
(усл.ед.):| Поставщики | Потребители | Мощности поставщиков | |||
 |  |  |  | ||
 | 3 | 1 80 | 2 | 1 | 80 |
 | 2 | 4 | 2 70 | 2 30 | 100 |
 | 1 80 | 3 40 | 5 | 2 0 | 120 |
| Мощности потребителей | 80 | 120 | 70 | 30 | 300 |