Добавлен: 05.02.2019
Просмотров: 440
Скачиваний: 9
ВОПРОСЫ К ИГА ЛФ СТАТИСТИКА
1.ПРОИЗВОДНУЮ
ФУНКЦИИ
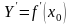МОЖНО РАССМАТРИВАТЬ КАК:
1. закон роста популяции бактерий;
2. изменение массы вещества;
3. мгновенную скорость изменения функции;
4. все выше перечисленное;
2.В ТОЧКЕ МАКСИМУМА ФУНКЦИИ ПРИЗВОДНАЯ ФУНКЦИИ:
1. остается постоянной;
2. меняет знак с «+» на «-»;
3. меняет знак с «-» на «+»;
4. увеличивается;
3.В ТОЧКЕ МИНИМУМА ФУНКЦИИ ПРИЗВОДНАЯ ФУНКЦИИ:
1. остается постоянной;
2. меняет знак с «+» на «-»;
3. меняет знак с «-» на «+»;
4. увеличивается;
4.КРИТИЧЕСКИМИ ТОЧКАМИ ФУНКЦИИ НАЗЫВАЮТСЯ ТОЧКИ, В КОТОРЫХ:
1. производная функции не существует;
2. производная функции меняет знак;
3. производная функции равна нулю или не существует;
4. производная функции равна нулю.
5.ТОЧКАМИ ЭКСТРЕМУМА ФУНКЦИИ НАЗЫВАЮТ:
1. критические точки;
2. точки максимума и минимума;
3. точки, в которых производная функции равна нулю;
4. точки перегиба.
6.С ГЕОМЕТРИЧЕСКОЙ ТОЧКИ ЗРЕНИЯ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ-ЭТО:
1. семейство кривых;
2. скорость изменения функции;
3. площадь криволинейной трапеции;
4. тангенс угла наклона касательной к графику функции в этой точке.
7.ИНТЕГРИРОВАНИЕ МЕТОДОМ ЗАМЕНЫ ПЕРЕМЕННОЙ ПРЕДПОЛАГАЕТ:
1. замену подынтегрального выражения на произведение;
2. замену интеграла от сложной функции на произведение двух интегралов;
3. ввод промежуточной переменной интегрирования.
4. замену подынтегрального выражения на сумму;
8.ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА ОПРЕДЕЛЯЕТ:
1. значение неопределенного интеграла;
2. значение определенного интеграла;
3. значение производной;
4. значение дифференциала.
9.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ ИСПОЛЬЗУЕТСЯ ДЛЯ ВЫЧИСЛЕНИЯ:
1. скорости роста популяции;
2. площади криволинейной трапеции;
3. скорости изменения температуры в системе;
4. скорости движения тела.
10.ПОРЯДОК ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ-ЭТО:
1. наименьший порядок производной функции;
2. наивысший порядок степени аргумента;
3. наивысший порядок производной функции;
4. наименьший порядок степени аргумента.
11.ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ-ЭТО УРАВНЕНИЕ, СОДЕРЖАЩЕЕ:
1. независимую переменную и ее степень любого порядка;
2. независимую переменную, функцию и ее степень любого порядка;
3. функцию и независимую переменную;
4. функцию, независимую переменную и производную функции любого порядка.
12.ЧАСТНОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ПОЛУЧАЮТ ПРИ:
1. подстановке конкретного значения постоянной C в уравнение;
2. подстановке заданных начальных значений х0 и y0 в уравнение;
3. подстановке в общее решение заданных начальных значений х0 и y0;
4. подстановке общего решения в уравнение.
13.СОБЫТИЯ НАЗЫВАЮТ СОВМЕСТИМЫМИ, ЕСЛИ:
1. наступление одного из событий не исключает появление другого,
2. наступление одного из них сопровождается наступлением другого,
3. в условиях опыта произойдут только эти события и никакие другие.
4. верны все варианты
14.СОБЫТИЯ НАЗЫВАЮТ ЕДИНСТВЕННО ВОЗМОЖНЫМИ:
1. если в условиях данного опыта произойдут только эти события и никакие другие,
2. если наступление одного из событий исключает появление другого,
3. если события не могут произойти одновременно в условиях данного опыта.
4. верны все варианты
15.ПОД ПРОТИВОПОЛОЖНЫМИ СОБЫТИЯМИ ПОНИМАЮТ:
1. два единственно возможных события образующих полную группу.
2. если наступление одного из событий исключает появление другого,
3. события, которые в результате опыта могут наступить, но могут и не наступить, при условии что эти события образуют полную группу.
4. верны все варианты
16.ВЕРОЯТНОСТЬЮ СОБЫТИЯ НАЗЫВАЕТСЯ:
1. отношение числа благоприятных исходов к общему числу возможных исходов
2. численная мера степени объективной возможности не появления этого события,
3. событие, если оно обязательно произойдет в условиях данного опыта.
4. верны все варианты
17.ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ СОБЫТИЙ, ОБРАЗУЮЩИХ ПОЛНУЮ ГРУППУ
РАВНА:
1.нулю
2.единице
3.разности между единицей и вероятностью наступления события А.
4. 0,5
18.СУММОЙ ДВУХ СОБЫТИЙ А И В ЯВЛЯЕТСЯ СОБЫТИЕ С, КОТОРОЕ ЗАКЛЮЧАЕТСЯ:
1. в появлении либо события А, либо события В,
2. в одновременном появлении событий А и В,
3. в исключении события А и события В.
4. верны все варианты
19.ФОРМУЛА БАЙЕСА ПОЗВОЛЯЕТ ОПРЕДЕЛИТЬ:
1.доопотные вероятности,
2.послеопотные вероятности гипотез
3.полную вероятность.
4. вероятность события
20.ЗНАМЕНАТЕЛЬ В ФОРМУЛЕ БАЙЕСА ЭТО:
1.доопотные вероятности,
2.послеопотные вероятности,
3.полная вероятность.
4. классическая вероятность
21.ДИСКРЕТНОЙ НАЗЫВАЮТ ТАКУЮ СЛУЧАЙНУЮ ВЕЛИЧИНУ:
1. которая принимает некоторые значения из некоторого интервала,
2. которая принимает только отдельные числовые значения в определенном интервале,
3. значения которой можно просчитать.
4. нет правильного ответа
22.НЕПРЕРЫВНОЙ НАЗЫВАЮТ ТАКУЮ СЛУЧАЙНУЮ ВЕЛИЧИНУ:
1. которая принимает некоторые значения из некоторого интервала,
2. значения которой лежат в определенном интервале,
3. значения которой можно просчитать.
4. нет правильного ответа
23.ДИСПЕРСИЯ ХАРАКТЕРИЗУЕТ:
1.среднее значение случайной величины,
2.степень рассеяния случайной величины.
3.функцию распределения случайной величины.
4. нет правильного ответа
24.ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА ПОДЧИНЯЕТСЯ:
1. распределению Пуассона,
2. нормальному распределению,
3. биноминальному распределению.
4. биноминальному распределению и распределению Пуассона,
25.БИНОМИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПРИМЕНЯЕТСЯ:
1.в случае редких событий,
2.если вероятность единичного события больше 0.1,
3.если заданное значение случайной непрерывной величины находится
в определенном интервале.
4. нет правильного ответа
26.В СЛУЧАЕ РЕДКИХ СОБЫТИЙ ПРИМЕНЯЕТСЯ:
1. биноминальное распределение,
2. нормальное распределение,
3. распределение Пуассона.
4. нет правильного ответа
27.МАТЕМАТИЧЕСКИМ ОЖИДАНИЕМ СЛУЧАЙНОЙ ВЕЛИЧИНЫ НАЗЫВАЕТСЯ:
1. сумма произведений всех возможных значений случайной величины на их вероятности,
2. корень квадратной из дисперсии,
3. совокупность всех значений этой величины с соответствующими вероятностями.
4. нет правильного ответа
28. ГИСТОГРАММА ЭТО ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЗАВИСИМОСТИ:
-
значений функций распределения от значений случайной величины
-
функции плотности вероятности распределения от случайной величины
-
дисперсии от значений случайной величины
-
нет правильного ответа
-
ЗАВИСИМОСТЬ НАЗЫВАЕТСЯ ФУНКЦИОННАЛЬНОЙ, ЕСЛИ:
-
одному значению одной переменной величины соответствует множество значений другой,
-
одному значению одной переменной величины соответствует одно значение другой,
-
одному значению одной переменной величины соответствует два значений другой.
30.ОДНОМУ ЗНАЧЕНИЮ ОДНОЙ ПЕРЕМЕННОЙ СООТВЕТСТВУЕТ МНОЖЕСТВО ЗНАЧЕНИЙ ДРУГОЙ, ТО ТАКАЯ ЗАВИСИМОСТЬ ЯВЛЯЕТСЯ:
1.функциональной зависимостью,
2.обратнопропорциональной,
3.корреляционной,
4.прямопропорциональной.
ОТВЕТЫ
|
№ вопроса |
ответ |
№вопроса |
ответ |
№вопроса |
ответ |
|
1 |
4 |
11 |
4 |
21 |
3 |
|
2 |
2 |
12 |
3 |
22 |
2 |
|
3 |
3 |
13 |
1 |
23 |
2 |
|
4 |
3 |
14 |
1 |
24 |
4 |
|
5 |
2 |
15 |
2 |
25 |
2 |
|
6 |
1 |
16 |
1 |
26 |
3 |
|
7 |
3 |
17 |
2 |
27 |
1 |
|
8 |
2 |
18 |
1 |
28 |
2 |
|
9 |
2 |
19 |
2 |
29 |
2 |
|
10 |
3 |
20 |
3 |
30 |
3 |
Зав.кафедрой биофизики и математики
д.м.н. Е.Н.Денисов