ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Факультет естествознания группа 211 ФПК
Специальность/ОП Физика
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
Количество билетов 25 количество обучающихся 10
Утверждено на заседании Академического комитета
протокол № _________ от «_____» ____________20___
Решение экспертной комиссии ______________________________________
Дата экзамена____________ время ____________ ауд. _________________
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Дайте определение скалярного поля. Приведите примеры скалярного поля. Покажите как графически изображается скалярное поле. Приведите примеры. Дайте инвариантное определение градиента скалярного поля. Перечислите основные свойства градиента скалярного поля. Покажите как вычисляется модуль градиента скалярного поля. | 35 | |
| 2 | Запишите уравнение Лапласа в цилиндрических координатах. Найдите решение этого уравнения методом Фурье. Назовите специальные функции, которые встречаются при решении данного уравнения. | 35 | |
| 3 | Вычислите дивергенцию векторного поля 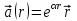 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | В математической физике используют основные формулы векторной алгебры. Дайте определения скалярного и векторного произведений двух векторов. Приведите их основные свойства. Выразите скалярное и векторное произведения двух векторов через проекции на координатные оси. Запишите формулу двойного векторного произведения. Покажите основное свойство смешанного произведения трех векторов. | 35 | |
| 2 | Рассмотрите задачу об охлаждении бесконечно длинного стержня. Решите задачу методом Фурье. | 35 | |
| 3 | Определите градиент скалярного поля 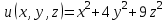 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Дайте определение векторного поля. Приведите примеры векторного поля. Покажите как графически изображается векторное поле. Приведите примеры. Выведите формулу векторных линий. | 35 | |
| 2 | Запишите уравнение Лапласа в сферических координатах. Найдите решение этого уравнения методом Фурье. Назовите специальные функции, которые встречаются при решении данного уравнения. | 35 | |
| 3 | Найдите градиент скалярного поля 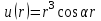 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Покажите как определяется поток векторного поля через элементарную поверхность и через полную замкнутую поверхность. Сформулируйте теорему Остроградского-Гаусса. Запишите математическое выражение этой теоремы. Приведите пример определения потока векторного поля с помощью теоремы Остроградского-Гаусса. | 35 | |
| 2 | Запишите уравнение Бесселя. Изложите методику решения уравнения Бесселя. Назовите цилиндрические функции. Запишите выражения для цилиндрических функций. | 35 | |
| 3 | Вычислите градиент скалярного поля 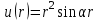 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Дайте инвариантное определение дивергенции векторного поля. Приведите основные свойства дивергенции векторного поля. Запишите формулу, по которой вычисляется дивергенция векторного поля в декартовых координатах. | 35 | |
| 2 | Рассмотрите задачу о колебаниях бесконечно длинной струны. Приведите постановку задачи и найдите решение этого уравнения методом Даламбера. | 35 | |
| 3 | Определите градиент скалярного поля 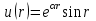 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Дайте определение циркуляции векторного поля. Приведите инвариантное определение ротора векторного поля. Запишите формулу для вычисления ротора векторного поля в декартовых координатах. Приведите основные свойства ротора векторного поля. Сформулируйте теорему Стокса. Запишите математическое выражение этой теоремы. | 35 | |
| 2 | Запишите обобщенное и простое уравнение Лежандра. Изложите методику решения уравнения Лежандра. Запишите формулы Родриго для полиномов Лежандра. | 35 | |
| 3 | Найдите дивергенцию векторного поля 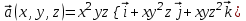 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Запишите выражение для оператора Гамильтона. Назовите дифференциальные операции первого порядка. Выразите их с помощью оператора Гамильтона. Найдите результат действия оператора Гамильтона на произведения скалярных и векторных полей. | 35 | |
| 2 | Во многих задачах физики применяются дифференциальные уравнения в частных производных второго порядка. Приведите не менее пяти наиболее часто вcтречающихся видов таких уравнений. | 35 | |
| 3 | Вычислите дивергенцию векторного поля 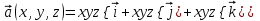 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Дайте определение векторного поля. Приведите классификацию векторных полей. Напишите условие соленоидальности, условие потенциальности векторного поля. Дайте определение гармонического векторного поля. Напишите формулу, выражающую условие гармоничности векторного поля. | 35 | |
| 2 | Введите основные понятия и определения теории дифференциального уравнения в частных производных. Приведите классификацию дифференциальных уравнений в частных производных. Напишите формулу, выражающую общий вид линейного дифференциального уравнения в частных производных второго порядка. | 35 | |
| 3 | Определите поток векторного поля 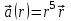 через произвольную замкнутую поверхность, ограничивающую объем V. через произвольную замкнутую поверхность, ограничивающую объем V. | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Найдите результат применения оператора Гамильтона к произведению двух векторных полей. Докажите формулу 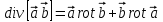 , используя непосредственное вычисление. , используя непосредственное вычисление. | 35 | |
| 2 | Назовите известные вам методы решения дифференциальных уравнений в частных производных. Какова сущность метода разделения переменных? Приведите пример использования метода разделения переменных при решении дифференциального уравнения в частных производных. | 35 | |
| 3 | Вычислите градиент скалярного поля 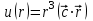 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Назовите дифференциальные операции второго порядка. Используя оператор Гамильтона, найдите выражения для дифференциальных операций второго порядка. Составьте таблицу дифференциальных операций второго порядка. Запишите выражение оператора Лапласа в декартовых координатах. | 35 | |
| 2 | Дайте определение дифференциального уравнения в частных производных. Назовите типы дифференциальных уравнений в частных производных. Приведите их примеры. Покажите как определять тип дифференциального уравнения в частных производных. | 35 | |
| 3 | Найдите дивергенцию векторного поля 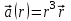 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Введите криволинейные координаты. Напишите уравнения, определяющие координатные поверхности. Дайте определение координатных линий. Запишите соотношения, доказывающие что криволинейная система координат является ортогональной. Выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи коэффициентов Ламе. | 35 | |
| 2 | Приведите классификацию краевых задач. Дайте определение задачи Коши. | 35 | |
| 3 | Определите поток векторного поля 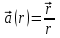 через произвольную замкнутую поверхность, ограничивающую объем V. через произвольную замкнутую поверхность, ограничивающую объем V. | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Запишите основные дифференциальные операции в криволинейных координатах. Приведите формулы для вычисления коэффициентов Ламе. | 35 | |
| 2 | Назовите методы решения дифференциальных уравнений в частных производных. Напишите в чем заключается метод функции Грина. Приведите пример использования метода функции Грина. | 35 | |
| 3 | Вычислите градиент скалярного поля 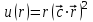 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Назовите цилиндрические координаты. Покажите связь цилиндрических и декартовых координат. Сделайте рисунок и покажите координатные поверхности и координатные линии в цилиндрической системе координат. Определите коэффициенты Ламе в цилиндрической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов. Запишите основные дифференциальные операции в цилиндрических координатах. | 35 | |
| 2 | Запишите уравнение Пуассона для потенциала электростатического поля. Сформулируйте граничное условие для данной задачи. Примените метод функции Грина для определения потенциала электростатического поля. | 35 | |
| 3 | Найдите ротор векторного поля 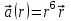 . . | 30 | |
Дисциплина Методы математической физики
Преподаватель Калжанова Г.К.
| № | Вопросы/задания | Балл | Набранный балл |
| 1 | Дайте определение вектор-функции скалярного аргумента. Приведите примеры вектор-функций из разных разделов физики. Запишите правила дифференцирования вектор-функции. Приведите правила интегрирования вектор-функции. | 35 | |
| 2 | Назовите физические задачи, описываемые уравнениями параболического типа. Перечислите методы решения уравнений параболического типа и с помощью одного из них решите уравнение данного типа. | 35 | |
| 3 | Вычислите 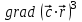 . . | 30 | |