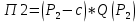Добавлен: 06.12.2023
Просмотров: 833
Скачиваний: 82
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 3
Вариант 4
Известно, что для потребительского набора
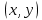функция полезности потребителя задана уравнением 
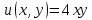Общий доход m, которым располагает потребитель, составляет 480 ден. ед. Цена товара 
– 
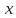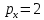ден. ед., цена товара 
– 
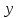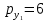ден. ед. Предположим, что цена товара 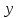увеличивается до уровня 
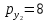ден.ед.Осуществите следующие действия:
- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;
- определите эффект замены (по Хиксу);
- определите эффект дохода (по Хиксу);
- определите общий эффект (по Хиксу);
- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Решение
1. Бюджетное ограничение по заданным значениям принимает вид:
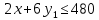
Оптимальный выбор потребителя:
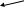
Кривые безразличия
8
y
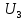
x
6
Рисунок 3.1
Графическое представление оптимальной точки – это точка касания бюджетного ограничения потребителя и кривой безразличия. Исходя из этого, в точке оптимума угол наклона кривой безразличия (
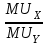) равен углу наклона бюджетного ограничения (
). 
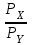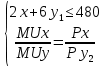
Решая данную систему для функции вида Кобба-Дугласа
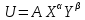, находим выражения для оптимального количества товаров Х и У.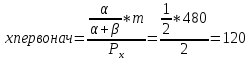
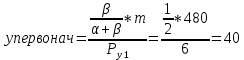
Первоначально потребитель потреблял 40 ед. товара x и 15 ед. товара y; при этом он достигал уровня полезности:
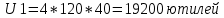
Аналогично можно рассчитать объемы товаров x и y после изменения цены на товар y, то есть конечную оптимальную точку.
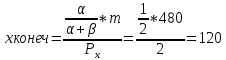
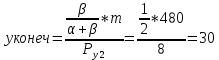
После повышения цены товара y, потребитель уменьшил объем потребления этого товара на 10 единиц. Таким образом, общий эффект от повышения цены товара y равен –10 ед.
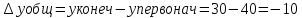
Общий эффект показывает, как изменился объем потребления товара при изменении его цены.
2. Для расчета по методу Хикса, необходимо построить дополнительное (вспомогательное) бюджетное ограничение, параллельное новому бюджетному ограничению (с новыми ценами), которое бы являлось касательным к первоначальной кривой безразличия.
Точка 1 – первоначальная оптимальная точка потребителя (касание первоначального бюджетного ограничения и первоначальной кривой безразличия). Точка 2 – конечная оптимальная точка потребителя (касание нового бюджетного ограничения и новой кривой безразличия). Точка 3 – вспомогательная точка по методу Хикса (касание вспомогательного бюджетного ограничения и первоначальной кривой безразличия).
Рисунок 3.2
Для расчета координат вспомогательной (промежуточной точки) необходимо решить систему из двух уравнений:
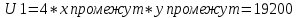
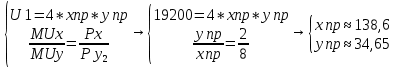
Подробное решение:
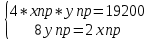
Из второго уравнения выразим yпр:
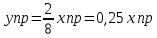
Подставим в первое:
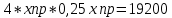
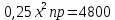
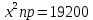
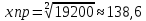
Найдем, чему равен yпр:
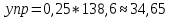
Эффект замены: при повышении цены товара y, объем потребления товара y (при сохранении потребителем первоначального уровня полезности) уменьшился на 5,35 ед.
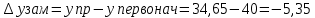
3. Эффект дохода: при повышении цены товара y, что эквивалентно росту реального дохода потребителя, объем потребления товара y уменьшился на 4,65 ед.
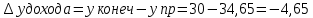
Прямая зависимость между изменением реального дохода и объемом потребления, следовательно, y – товар нормальный.
4. Выполним проверку:
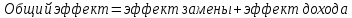
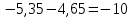
Вывод: товар y является нормальным (качественным товаром). Закон спроса (обратная зависимость между ценой товара и объемом потребления) не нарушен.
Практическое задание 4
Вариант 4
Технологическая норма замещения факторов L и K равна MRS = –4. Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора K на 1 единицу. Сколько дополнительных единиц фактора L потребуется фирме?
Решение:
Условие оптимального использования ресурсов:
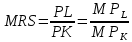
При этом:
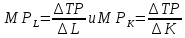
Так как фирма сократит использование фактора K на 1 единицу, то К= –1, а объем выпуска остается неизменным. Составим уравнение:
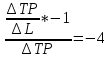
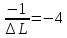
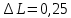
Вывод: в результате проведенных расчетов, фирме потребуется 0,25 дополнительных фактора L.
Практическое задание 5
Задача 1
Предположим, что на рынке действуют две фирмы, функции общих издержек TC заданы уравнениями:
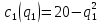и 
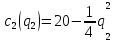. Рыночный спрос описывается функцией:
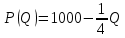,где
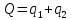.Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:
- фирмы конкурируют по Курно;
- фирмы конкурируют по Бертрану;
- фирмы конкурируют по сценарию Штакельберга.
Изобразите решение на графике.
Решение:
1. Стратегия по Курно предполагает, что фирмы изначально выбирают объем производства, обладая полной информацией о своих конкурентах. Решения о выборе объема принимаются одновременно.
Решение задачи по Курно:
Подставим общий выпуск двух фирм в формулу отраслевого спроса, получим:
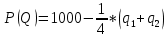
Распишем прибыли олигополистов:
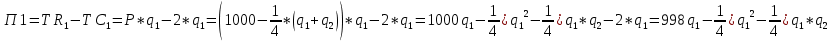
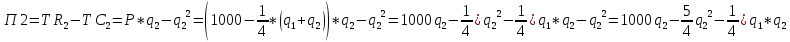
Каждая фирма стремится к максимуму прибыли.
Найдём максимум функций прибыли. Для этого приравняем к нулю первые производные полученных функций и найдём оптимальный объём выпуска:
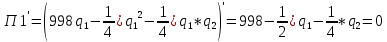
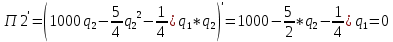
Уравнение реакции для первой фирмы:
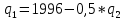
Уравнение реакции для второй фирмы:
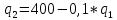
Точка пересечения этих линий определяет рыночное равновесие для монополистов представлена на рисунке 5:
Равновесие Курно
3992
400
q1
4000
1996
0
q2
Рисунок 5
Решим систему из двух уравнений реакции дуополистов, получим равновесные значения выпуска для первой и второй фирмы.
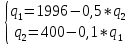
Подставим второе уравнение в первое:
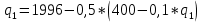
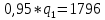
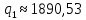
Полученное значение подставим во второе:
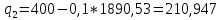
Подставив равновесные значения q*1 и q*2 в функцию отраслевого спроса, найдём цену равновесия:
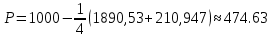
2. Стратегия по Бертрану предполагает, что фирмы изначально выбирают цену, обладая полной информацией о своих конкурентах. Решения о выборе цены принимаются одновременно. Важным условием такой модели является полная взаимозаменяемость товаров. Очевидно, что потребители будут покупать товар по наименьшей доступной цене. Тогда фирмы, которые установили не минимальную цену, получат нулевую выручку.
Рынок товара контролируют две фирмы. Соответственно, они выбирают цены ????1 и ????2. Тогда функции прибыли этих фирм будут принимать следующий вид:
Если
то
