Файл: Httpsfuture2day runejronnyeseti#.docx

В рамках кибернетики развивалось и направление, которое мы привыкли называть нейросетевым. Юрген Шмитхубер, создатель известной нейросетевой архитектуры LSTM, известный в наши дни также как историк глубокого обучения, часто ссылается в своих выступлениях на вклад советских учёных в становление этого направления.

В 60-ые годы в СССР большими тиражами выходило несколько серьёзных тематических изданий, и, судя по наукометрической статистике, изрядная доля мировых коннекционистских исследований издавалась именно на русском языке. Коннекционизм в какой-то момент оказался настолько популярен, что им занялись не только в метрополии, но и в других городах и республиках, например в Армении и Грузии. К сожалению, пока что оцифрована лишь небольшая доля публикаций тех лет, большинство работ можно найти только в оффлайн-библиотеках.

---

«Шла машина из Тамбова» или чем занимался Маккарти в СССР

Несмотря на железный занавес, советские исследователи не варились в собственном соку. Существовал интенсивный обмен идеями между нашими и заграничными учёными. Если говорить про кибернетику, в 1965 году в рамках международного обмена группа западных исследователей посетила СССР. 

Сначала они заехали в Киев и познакомились с академиком Виктором Глушковым, автором концепции ОГАС, а также с профессором Киевского политехнического института Алексеем Ивахненко, о котором речь пойдёт далее. Затем последовал визит в Тбилиси, где западных гостей встречал директор Института систем управления Академии наук Грузинской ССР Арчил Элиашвили. Там над многослойными (или, как их называли в советской литературе, «многорядными») перцептронами работали исследователи, имена которых сейчас даже человеку, подкованному в теме, мало что скажут. Они занимались в том числе системами распознавания речи. Уинстон Нельсон (Winston Nelson) из Лаборатории Белла, участвовавший в делегации, описывает визит в грузинскую лабораторию так:

«Там на полу был небольшой робот, и он передвигался согласно произносимым вслух командам. <...> А затем мы вернулись в офис директора, где стоял длинный стол, уставленный вазами с фруктами, хачапури и превосходным грузинским коньяком».


Помимо Одессы, Киева и Тбилиси, делегация посетила Баку, Москву, Минск, Ленинград и несколько других городов союзных республик. В Москве Маккарти встретился со своим старым знакомым — академиком Андреем Ершовым. Коллеги познакомились в декабре 1958 года в Великобритании на Конференции по автоматизации мыслительных процессов. После визита в Москву Маккарти в сопровождении Ершова отправился в новосибирский Академгородок, откуда через Москву вернулся домой (в реалиях холодной войны, когда Новосибирск был одним из полузакрытых научных центров, Ершову стоило больших трудов согласовать этот визит). 

Через три года Маккарти ещё раз приехал в Академгородок

---

 — теперь уже на два месяца и в качестве сотрудника Вычислительного центра: он прочитал курс по верификации программ в Новосибирском университете. В ходе одной из поездок Маккарти познакомился с Александром Кронродом, который работал над шахматной программой, наследницей которой стала знаменитая «Каисса», и договорился о проведении первого в мире шахматного матча между компьютерными программами. В этом матче в 1967-м году советская шахматная программа, разработанная в Институте теоретической и экспериментальной физики, победила программу Стэнфордского университета со счётом 3-1.



Типы Нейронных сетей

https://tproger.ru/translations/neural-network-zoo-1/

Решение задач нейронными сетями

http://www.gotai.net/documents/doc-art-003-05.aspx

В данной главе описано несколько базовых задач для нейронных сетей и основных или исторически первых методов настройки сетей для их решения:

1. 
   Классификация (с учителем) (персептрон Розенблатта [1-3]).
   
2. 
   Ассоциативная память (сети Хопфилда [4-7]).
   
3. 
   Решение систем линейных уравнений (сети Хопфилда [8]).
   
4. 
   Восстановление пробелов в данных (сети Хопфилда).
   
5. 
   Кластер-анализ и классификация (без учителя) (сети Кохонена [9-12]).
   

Начнем мы, однако, не с сетей, а с систем, состоящих из одного элемента.

1. Настройка одноэлементных систем для решения задач

Даже системы из одного адаптивного сумматора находят очень широкое применение. Вычисление линейных функций необходимо во многих задачах. Вот неполный перечень «специальностей» адаптивного сумматора:

6. 
   Линейная регрессия и восстановление простейших закономерностей [13-14];
   
7. 
   Линейная фильтрация и адаптивная обработка сигналов [15];
   
8. 
   Линейное разделение классов и простейшие задачи распознавания образов [16-18].
   

Задача линейной регрессии состоит в поиске наилучшего линейного приближения функции, заданной конечным набором значений: дана выборка значений вектора аргументов x¹ , ..., x^m, заданы значения функции F в этих точках: F(x ⁱ)=f_i, требуется найти линейную (неоднородную) функцию j(x)=(a,x)+a₀, ближайшую к

---

F. Чтобы однозначно поставить задачу, необходимо доопределить, что значит «ближайшую». Наиболее популярен метод наименьших квадратов, согласно которому j ищется из условия

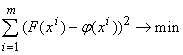(1)

Необходимо особенно подчеркнуть, что метод наименьших квадратов не является ни единственным, ни наилучшим во всех отношениях способом доопределения задачи регрессии. Его главное достоинство ‑ квадратичность минимизируемого критерия и линейность получаемых уравнений на коэффициенты j.

Явные формулы линейной регрессии легко получить, минимизируя квадратичный критерий качества регрессии. Обозначим



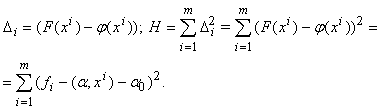
Найдем производные минимизируемой функции H по настраиваемым параметрам:



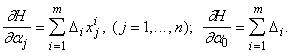
где x ⁱ_j ‑ j-я координата вектора x ⁱ.

Приравнивая частные производные H нулю, получаем уравнения, из которых легко найти все a_j (j=0,...,n). Решение удобно записать в общем виде, если для всех i =1,...,m обозначить и рассматривать n+1-мерные векторы данных x ⁱ и коэффициентов a. Тогда



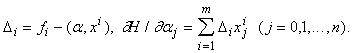
Обозначим p n+1-мерный вектор с координатами 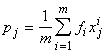; Q - матрицу размером (n+1)´(n+1) с элементами .

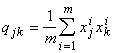В новых обозначениях решение задачи линейной регрессии имеет вид:

j(x)=(a,x), a=Q‑1p.

(2)

Приведем это решение в традиционных обозначениях математической статистики. Обозначим M_î среднее значение j-й координаты векторов исходной выборки:

---

.

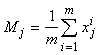
Пусть M ‑ вектор с координатами M_î. Введем также обозначение s_j для выборочного среднеквадратичного отклонения:



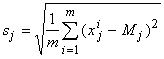
Величины s_j задают естественный масштаб для измерения j-х координат векторов x. Кроме того, нам потребуются величина s_f и коэффициенты корреляции f с j-ми координатами векторов x ‑ r_fj:



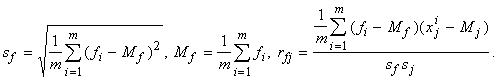
Вернемся к n-мерным векторам данных и коэффициентов. Представим, что векторы сигналов проходят предобработку ‑ центрирование и нормировку и далее мы имеем дело с векторами y ⁱ:



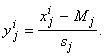
Это, в частности, означает, что все рассматриваемые координаты вектора x имеют ненулевую дисперсию, т.е. постоянные координаты исключаются из рассмотрения ‑ они не несут полезной информации. Уравнения регрессии будем искать в форме: j(y)=(b,y)+b₀. Получим:

b0=Mf, b=sfR‑1Rf,

(3)

где R_f ‑ вектор коэффициентов корреляции f с j-ми координатами векторов x, имеющий координаты r_fj, R ‑ матрица коэффициентов корреляции между координатами вектора данных:



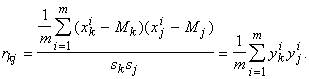
В задачах обработки данных почти всегда возникает вопрос о последовательном уточнении результатов по мере поступления новых данных (обработка данных «на лету»). Существует, как минимум, два подхода к ответу на этот вопрос для задачи линейной регрессии. Первый подход состоит в том, что изменения в коэффициентах регрессии при поступлении новых данных рассматриваются как малые и в их вычислении ограничиваются первыми порядками теории возмущений. При втором подходе для каждого нового вектора данных делается шаг изменений коэффициентов, уменьшающий ошибку регрессии D² на вновь поступившем векторе данных. При этом «предыдущий опыт» фиксируется только в текущих коэффициентах регрессии.

В рамках первого подхода рассмотрим

---