ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Сети Хопфилда
Перейдем от одноэлементных систем к нейронным сетям. Пусть aij ‑ вес связи, ведущей от j-го нейрона к i -му (полезно обратить внимание на порядок индексов). Для полносвязных сетей определены значения aij при всех i ,j, для других архитектур связи, ведущие от j-го нейрона к i -му для некоторых i ,j не определены. В этом случае положим aij=0.
В данном разделе речь пойдет в основном о полносвязных сетях. Пусть на выходах всех нейронов получены сигналы xj (j-номер нейрона). Обозначим x вектор этих выходных сигналов. Прохождение вектора сигналов x через сеть связей сводится к умножению матрицы (aij) на вектор сигналов x. В результате получаем вектор входных сигналов нелинейных элементов нейронов:
.Это соответствие «прохождение сети º умножение матрицы связей на вектор сигналов» является основой для перевода обычных численных методов на нейросетевой язык и обратно. Практически всюду, где основной операцией является умножение матрицы на вектор, применимы нейронные сети. С другой стороны, любое устройство, позволяющее быстро осуществлять такое умножение, может использоваться для реализации нейронных сетей.
В частности, вычисление градиента квадратичной формы
может осуществляться полносвязной сетью с симметричной матрицей связей: 
(
). Именно это наблюдение лежит в основе данного раздела.Что можно сделать, если мы умеем вычислять градиент квадратичной формы?
В первую очередь, можно методом наискорейшего спуска искать точку минимума многочлена второго порядка. Пусть задан такой многочлен:
. Его градиент равен 
. Этот вектор может быть получен при прохождении вектора x через сеть с весами связей
при условии, что на входной сумматор каждого нейрона по дополнительной связи веса b подается стандартный единичный сигнал.Зададим теперь функционирование сети формулой
 | (8) |
Нелинейных элементов вовсе не нужно! Каждый (j-й) нейрон имеет входные веса
для связей с другими нейронами (i ¹j), вес 
для постоянного единичного входного сигнала и вес 
для связи нейрона с самим собой (передачи на него его же сигнала с предыдущего шага). Выбор шага h>0 может вызвать затруднение (он зависит от коэффициентов минимизируемого многочлена). Есть, однако, простое решение: в каждый момент дискретного времени T выбирается свое значение 
. Достаточно, чтобы шаг стремился со временем к нулю, а сумма шагов ‑ к бесконечности (например, 
).Итак, простая симметричная полносвязная сеть без нелинейных элементов может методом наискорейшего спуска искать точку минимума квадратичного многочлена.
Решение системы линейных уравнений
сводится к минимизации многочлена
Поэтому решение системы может производиться нейронной сетью. Простейшая сеть, вычисляющая градиент этого многочлена, не полносвязна, а состоит из двух слоев: первый с матрицей связей
, второй ‑ с транспонированной матрицей 
. Постоянный единичный сигнал подается на связи с весами
на первом слое. Минимизация этого многочлена, а значит и решение системы линейных уравнений, может проводиться так же, как и в общем случае, в соответствии с формулой 
. Усовершенствованные варианты алгоритма решения можно найти в работах Сударикова [8].Небольшая модификация позволяет вместо безусловного минимума многочлена второго порядка P искать точку условного минимума с условиями
, то есть точку минимума P в ограничении на аффинное многообразие, параллельное некоторым координатным плоскостям. Для этого вместо формулы
следует использовать:
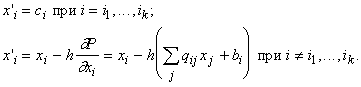 | (9) |
Устройство, способное находить точку условного минимума многочлена второго порядка при условиях вида
позволяет решать важную задачу ‑ заполнять пробелы в данных (и, в частности, строить линейную регрессию).Предположим, что получаемые в ходе испытаний векторы данных подчиняются многомерному нормальному распределению:
,где Mx ‑ вектор математических ожиданий координат,
, 
‑ ковариационная матрица, n ‑ размерность пространства данных,
.
Напомним определение матрицы
:
,где M ‑ символ математического ожидания, нижний индекс соответствует номеру координаты.
В частности, простейшая оценка ковариационной матрицы по выборке дает:
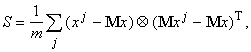
где m ‑ число элементов в выборке, верхний индекс j ‑ номер вектора данных в выборке, верхний индекс Т означает транспонирование, а Ä ‑ произведение вектора-столбца на вектор-строку (тензорное произведение).
Пусть у вектора данных x известно несколько координат:
. Наиболее вероятные значения неизвестных координат должны доставлять условный максимум показателю нормального распределения ‑ многочлену второго порядка 
(при условии ). Эти же значения будут условными математическими ожиданиями неизвестных координат при заданных условиях.Таким образом, чтобы построить сеть, заполняющую пробелы в данных, достаточно сконструировать сеть для поиска точек условного минимума многочлена
при условиях следующего вида: . Матрица связей Q выбирается из условия 
, где S ‑ ковариационная матрица (ее оценка по выборке).На первый взгляд, пошаговое накопление
по мере поступления данных требует слишком много операций ‑ получив новый вектор данных требуется пересчитать оценку S, а потом вычислить . Можно поступать и по-другому, воспользовавшись формулой приближенного обрашения матриц первого порядка точности:
Если же добавка D имеет вид
, то  | (10) |
Заметим, что решение задачи (точка условного минимума многочлена) не меняется при умножении Q на число. Поэтому полагаем:
где 1 ‑ единичная матрица, e>0 ‑ достаточно малое число,
‑ k+1-й вектор данных, 
‑ среднее значение вектора данных, уточненное с учетом : = 
В формуле для пошагового накопления матрицы Q ее изменение DQ при появлении новых данных получается с помощью вектора y=
, пропущенного через сеть: 
, где z=Qy. Параметр e выбирается достаточно малым для того, чтобы обеспечить положительную определенность получаемых матриц (и, по возможности, их близость к истинным значениям Q).Описанный процесс формирования сети можно назвать обучением. Вообще говоря, можно проводить формальное различение между формированием сети по явным формулам и по алгоритмам, не использующим явных формул для весов связей (неявным). Тогда термин «обучение» предполагает неявные алгоритмы, а для явных остается название «формирование». Здесь мы такого различия проводить не будем.
Если при обучении сети поступают некомплектные данные
с отсутствием значений некоторых координат, то сначала эти значения восстанавливаются с помощью имеющейся сети, а потом используются в ее дальнейшем обучении.