Файл: Httpsfuture2day runejronnyeseti#.docx

Во всех задачах оптимизации существенную роль играет вопрос о правилах остановки: когда следует прекратить циклическое функционирование сети, остановиться и считать полученный результат ответом? Простейший выбор ‑ остановка по малости изменений: если изменения сигналов сети за цикл меньше некоторого фиксированного малого d (при использовании переменного шага d может быть его функцией), то оптимизация заканчивается.

До сих пор речь шла о минимизации положительно определенных квадратичных форм и многочленов второго порядка. Однако самое знаменитое приложение полносвязных сетей связано с увеличением значений положительно определенных квадратичных форм. Речь идет о системах ассоциативной памяти [4-7,9,10,12].

Предположим, что задано несколько эталонных векторов данных и при обработке поступившего на вход системы вектора x требуется получить на выходе ближайший к нему эталонный вектор. Мерой сходства в простейшем случае будем считать косинус угла между векторами ‑ для векторов фиксированной длины это просто скалярное произведение. Можно ожидать, что изменение вектора x по закону

,

(11)

где h ‑ малый шаг, приведет к увеличению проекции x на те эталоны, скалярное произведение на которые больше.

Ограничимся рассмотрением эталонов, и ожидаемых результатов обработки с координатами . Развивая изложенную идею, приходим к дифференциальному уравнению

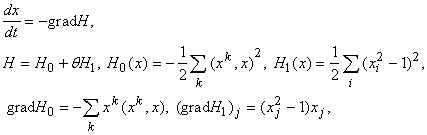(12)

где верхними индексами обозначаются номера векторов-эталонов, нижними ‑ координаты векторов.

Функция H называется «энергией» сети, она минимизируется в ходе функционирования. Слагаемое

---

вводится для того, чтобы со временем возрастала проекция вектора x на те эталоны, которые к нему ближе, слагаемое обеспечивает стремление координат вектора x к . Параметр q определяет соотношение между интенсивностями этих двух процессов. Целесообразно постепенно менять q со временем, начиная с малых q<1, и приходя в конце концов к q>1.

Подробнее системы ассоциативной памяти рассмотрены в отдельной главе. Здесь же мы ограничимся обсуждением получающихся весов связей. Матрица связей построенной сети определяется функцией , так как вычисляется непосредственно при j-м нейроне без участия сети. Вес связи между i -м и j-м нейронами не зависит от направления связи и равен

(13)

Эта простая формула имеет чрезвычайно важное значение для развития теории нейронных сетей. Вклад k-го эталона в связь между i -м и j-м нейронами ( ) равен +1, если i -я и j-я координаты этого эталона имеют одинаковый знак, и равен ‑1, если они имеют разный знак.

В результате возбуждение i -го нейрона передается j-му (и симметрично, от j-го к i -му), если у большинства эталонов знак i -й и j-й координат совпадают. В противном случае эти нейроны тормозят друг друга: возбуждение i -го ведет к торможению j-го, торможение i -го ‑ к возбуждению j-го (воздействие j-го на i -й симметрично). Это правило образования ассоциативных связей (правило Хебба) сыграло огромную роль в теории нейронных сетей.

---

3. Сети Кохонена для кластер-анализа и классификации без учителя

Построение отношений на множестве объектов - одна из самых загадочных и открытых для творчества областей применения искусственного интеллекта. Первым и наиболее распространенным примером этой задачи является классификация без учителя. Задан набор объектов, каждому объекту сопоставлен вектор значений признаков (строка таблицы). Требуется разбить эти объекты на классы эквивалентности.

Естественно, прежде, чем приступать к решению этой задачи, нужно ответить на один вопрос: зачем производится это разбиение и что мы будем делать с его результатом? Ответ на него позволит приступить к формальной постановке задачи, которая всегда требует компромисса между сложностью решения и точностью формализации: буквальное следование содержательному смыслу задачи нередко порождает сложную вычислительную проблему, а следование за простыми и элегантными алгоритмами может привести к противоречию со здравым смыслом.

Итак, зачем нужно строить отношения эквивалентности между объектами? В первую очередь - для фиксации знаний. Люди накапливают знания о классах объектов - это практика многих тысячелетий, зафиксированная в языке: знание относится к имени класса (пример стандартной древней формы: "люди смертны", "люди" - имя класса). В результате классификации как бы появляются новые имена и правила их присвоения.

Для каждого нового объекта мы должны сделать два дела:

12. 
    найти класс, к которому он принадлежит;
    
13. 
    использовать новую информацию, полученную об этом объекте, для исправления (коррекции) правил классификации.
    

Какую форму могут иметь правила отнесения к классу? Веками освящена традиция представлять класс его "типичным", "средним", "идеальным" и т.п. элементом. Этот типичный объект является идеальной конструкцией, олицетворяющей класс.

Отнесение объекта к классу проводится путем его сравнения с типичными элементами разных классов и выбора ближайшего. Правила, использующие типичные объекты и меры близости для их сравнения с другими, очень популярны и сейчас.

Простейшая мера близости объектов - квадрат евклидового расстояния между векторами значений их признаков (чем меньше расстояние ‑ расстояние - тем ближе объекты). Соответствующее определение признаков типичного объекта - среднее арифметическое значение признаков по выборке, представляющей класс.

---

Мы не оговариваем специально существование априорных ограничений, налагаемых на новые объекты - естественно, что "вселенная" задачи много 'уже и гораздо определеннее Вселенной.

Другая мера близости, естественно возникающая при обработке сигналов, изображений и т.п. - квадрат коэффициента корреляции (чем он больше, тем ближе объекты). Возможны и иные варианты - все зависит от задачи.

Если число классов m заранее определено, то задачу классификации без учителя можно поставить следующим образом.

Пусть {x^p } - векторы значений признаков для рассматриваемых объектов и в пространстве таких векторов определена мера их близости r{x,y}. Для определенности примем, что чем ближе объекты, тем меньше r. С каждым классом будем связывать его типичный объект. Далее называем его ядром класса. Требуется определить набор из m ядер y¹ , y² , ... y^m и разбиение {x^p} на классы:



минимизирующее следующий критерий

.

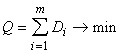(14)

где для каждого (i -го) класса ‑ сумма расстояний от принадлежащих ему точек выборки до ядра класса:

.

(15)

Минимум Q берется по всем возможным положениям ядер и всем разбиениям {x^p}на m классов Y _i.

Если число классов заранее не определено, то полезен критерий слияния классов: классы Y _i и Y_j сливаются, если их ядра ближе, чем среднее расстояние от элемента класса до ядра в одном из них. (Возможны варианты: использование среднего расстояния по обоим классам, использование порогового коэффициента, показывающего, во сколько раз должно расстояние между ядрами превосходить среднее расстояние от элемента до ядра и др.)

---

Использовать критерий слияния классов можно так: сначала принимаем гипотезу о достаточном числе классов, строим их, минимизируя Q, затем некоторые Y _i объединяем, повторяем минимизацию Q с новым числом классов и т.д.

Существует много эвристических алгоритмов классификации без учителя, основанных на использовании мер близости между объектами. Каждый из них имеет свою область применения, а наиболее распространенным недостатком является отсутствие четкой формализации задачи: совершается переход от идеи кластеризации прямо к алгоритму, в результате неизвестно, что ищется (но что-то в любом случае находится, иногда - неплохо).

Сетевые алгоритмы классификации без учителя строятся на основе итерационного метода динамических ядер. Опишем его сначала в наиболее общей абстрактной форме. Пусть задана выборка предобработанных векторов данных {x^p}. Пространство векторов данных обозначим E. Каждому классу будет соответствовать некоторое ядро a. Пространство ядер будем обозначать A. Для каждых xÎE и aÎA определяется мера близости d(x,a). Для каждого набора из k ядер a₁,...,a_k и любого разбиения {x^p} на k классов {x^p}=P₁ÈP₂È...ÈP_k определим критерий качества:

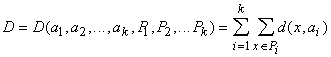(16)

Требуется найти набор a₁,...,a_k и разбиение {x^p}=P₁ÈP₂È...ÈP_k, минимизирующие D.

Шаг алгоритма разбивается на два этапа:

1-й этап - для фиксированного набора ядер a₁,...,a_k ищем минимизирующее критерий качества D разбиение {x^p}=P₁ÈP₂È...ÈP_k; оно дается решающим правилом: xÎP _i, если d(x,a _i )<d(x ,a_j ) при i ¹j, в том случае, когда для x минимум d(x,a) достигается при нескольких значениях i , выбор между ними может быть сделан произвольно;

2-й этап - для каждого P _i (i =1,...,k), полученного на первом этапе, ищется a _iÎA, минимизирующее критерий качества (т.е. слагаемое в D для данного i -

---