ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 102
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для нахождения касательных напряжений применяется формула
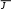T . (3.2)
p
Здесь Mx, My,T – изгибающие и крутящий момент, Jx, Jy – осевые
P
моменты инерции, J – полярный момент инерции, x, y– координаты точки, – радиус вектор точки поперечного сечения стержня, в котором определяются напряжения.
Используя равенство (3.1), (3.2), можно показать, что в поперечном сечении стержня в виде круга или кольца
максимальные значения и
находятся по соотношениям:
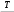
M
max W, max 2W, (3.3)
где M Mx My , W – момент со
противления сечения. Для круга радиуса R D/2
65
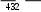W R3 D3 , (3.4)
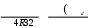
d
для кольца, с радиусами r d/2 , R D/2 (c d/ D),
W R4 r4
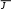T . (3.2)p
Здесь Mx, My,T – изгибающие и крутящий момент, Jx, Jy – осевые
P
моменты инерции, J – полярный момент инерции, x, y– координаты точки, – радиус вектор точки поперечного сечения стержня, в котором определяются напряжения.
Используя равенство (3.1), (3.2), можно показать, что в поперечном сечении стержня в виде круга или кольца
максимальные значения и
находятся по соотношениям:
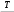
M
max W, max 2W, (3.3)
где M Mx My , W – момент со
противления сечения. Для круга радиуса R D/2
65
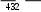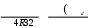
W R3 D3 , (3.4) d
для кольца, с радиусами r d/2 , R D/2 (c d/ D),
W R4 r4