М ИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ

НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ УКРАИНЫ

«КИЕВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ»

КАФЕДРА СИСТЕМ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ


АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ

АНАЛОГОВЫХ ФИЛЬТРОВ
О.ДА.722XX- XX


КУРСОВАЯ РАБОТА

по курсу

ОСНОВЫ АВТОМАТИЗАЦИИ ПРОЕКТИРОВАНИЯ

СЛОЖНЫХ ОБЪЕКТОВ И СИСТЕМ

Руководитель:			Выполнил:
Ладогубец В.В.
			студент гр. ДА-XX
Допущен к защите:
Защищено с оценкой:			Зач. книжка №ДА-XXXX

Киев 2000

Листов

2000


СОДЕРЖАНИЕ

Введение
1. Постановка задачи расчета ARC-фильтра.
2. Исходные данные к расчету
3. Нормирование характеристик и электрических величин
4. Аппроксимация нормированной передаточной функции фильтра нижних частот
5. Каскадная реализация фильтра по передаточной функции
6. Денормирование электрических величин.
7. Расчет ненормированной АЧХ фильтра
8. Описание программы, реализующей методику расчета
9. Расчет схемы фильтра с помощью разработанной программы
10. Моделирование полученной схемы фильтра с помощью пакета ALLTED
11. Сравнение полученных результатов
Выводы

---

Введение
Основным содержанием курсовой работы по курсу "Основы автоматизации проектирования сложных объектов и систем" является изучение и закрепление на практике изученного теоретического материала, касающегося методов проектирования активных аналоговых фильтров на резистивно-емкостных радиоэлементах (ARC-фильтров), находящих широкое применение при разработке электронных аналоговых и цифровых схем, систем автоматического управления и т.п.

Основная цель данной курсовой работы – приобрести навыки автоматизированного проектирования и моделирования принципиальных схем электронных устройств на базе комплексного использования пакета схемотехнического проектирования ALLTED.
1.Постановка задачи расчета ARC-фильтра
При проектировании аналоговых фильтров обычно задаются требования к амплитудно-частотной характеристике (АЧХ). Общепринятый способ задания таких требований для фильтра нижних (ФНЧ) частот показан на рис.1. При этом требования к фазовой характеристике не оговариваются. В этом случае для фильтра нижних частот обычно задается частота среза, неравномерность коэффициента передачи а_ф в полосе пропускания, граничная частота полосы задерживания f₁ , минимальное затухание в_ф коэффициента передачи в этой полосе.





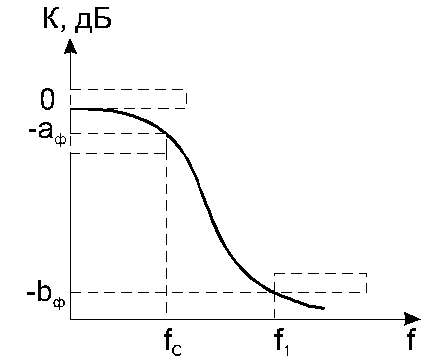
Рис.1. Задание требований к АЧХ фильтра нижних частот:
Таким образом, для фильтра нижних частот имеем :

полоса пропускания 0 f f_c ;

полоса задерживания f₁ f );
Основная задача, возникающая при проектировании аналоговых фильтров, – синтез оптимальной принципиальной схемы и расчет величин элементов по заданным требованиям к его АЧХ. Синтез можно разбить на два основных этапа.

На первом этапе решается задача аппроксимации–отыскание аналитической аппроксимирующей функции, которая с требуемой точностью воспроизводит заданную по условиям характеристику. При этом на аппроксимирующую функцию накладываются ограничения в виде необходимых и достаточных условий физической реализуемости.

---

На втором этапе решается задача реализации–отыскание совокупности цепей, имеющих характеристики, достаточно близкие к аппроксимирующей функции. В связи с тем, что любой физически осуществимой функции соответствует множество электрических схем, синтез неоднозначен.

Так как реализация функций высоких порядков затруднительна, функцию раскладывают на сомножители, обычно не выше второго порядка, которые и реализуют простейшими развязанными звеньями с активными элементами, например операционными усилителями (ОУ). При каскадном соединении таких звеньев удается получить результирующую схему с требуемыми свойствами, так как ее коэффициент передачи равен произведению коэффициентов передачи исходных звеньев.
2. Исходные данные к расчету

Вариантом 1 задания курсовой работой предусмотрено проектирование фильтра нижних частот с типом аппроксимации АЧХ по Баттерворту, Требования к АЧХ проектируемого фильтра приведены ниже :

---

Фильтр нижних частот

Вариант	FC,Гц	Аф,дБ	f1,Гц	Вф,дБ	Аппроксимация
1	500	2	800	30	по Баттерворту

3. Нормирование характеристик и электрических величин

Порядок величин, характеризующих параметры элементов электрических цепей, колеблется от 10^-12 Ф (для емкостей) до 10⁶...10⁷ Ом (для сопротивлений). Рабочие частоты колеблются в диапазоне от нескольких до миллионов герц. Таким образом, числовые значения электрических величин могут оказаться неудобными для практического использования. С другой стороны, свойства различных функций к операции синтеза не зависят от абсолютной величины коэффициентов этих функций. Поэтому целесообразно отделить рассмотрение свойств функций и техники синтеза (проектирования) от конкретных значений коэффициентов. Это достигается нормированием величин.

Вычисления можно упростить, если все функции сопротивления разделять на некоторую величину R₀, что эквивалентно изменению параметров пассивных элементов R, L и C следующим образом:

R'_н= , L'_н= , C'_н=CR₀.

Этот процесс называется изменением уровня (нормированием) сопротивлений. При таком преобразовании передаточные функции цепи, представляющие собой отношения напряжений или токов, не изменяются. При проектировании фильтров величину R₀ можно выбирать произвольно (обычно в пределах 1...100 к0м).

Для того чтобы сделать расчеты универсальными и упростить вычисления, используют также и нормирование частоты путем деления текущей частоты f на частоту f₀. В качестве нормирующей частоты f₀ в фильтрах нижних частот выбирают частоту среза f_c. Осуществив нормирование, решают задачу аппроксимации и реализации в нормированной частоте. При таком преобразовании частоты сопротивления R'_н не изменяются, индуктивное сопротивление уменьшается, а емкостное сопротивление увеличивается в 

---

₀ раз (₀=2f₀).

4.Аппроксимация нормированной передаточной функции фильтра нижних частот
В соответствии с заданием на курсовую работу для аппроксимации амплитудно-частотной характеристики проектируемого фильтра нижних частот должна использоваться максимально плоская аппроксимация амплитудно-частотной характеристики (аппроксимация Баттерворта)
В случае ФНЧ нормирующей частотой является частота среза, т.е. f₀=f_c. При аппроксимации нормированной АЧХ по Баттерворту передаточная функция представляется и виде

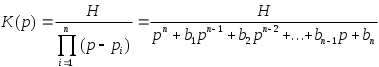(1)

Здесь P_i - полюсы передаточной функции,



Аппроксимация по Баттерворту дает хорошее приближение АЧХ в точке F=0 (рис.2,а). По мере удаления от нее погрешность аппроксимации возрастает и достигает максимального значения на границе полосы пропускания (F=1). Нормированную частоту F₁, определяющую начало полосы задерживания, находят следующим образом:

F₁=f₁/f_c.

В полосе задерживания модуль передаточной функции фильтра Баттерворта также монотонно уменьшается.


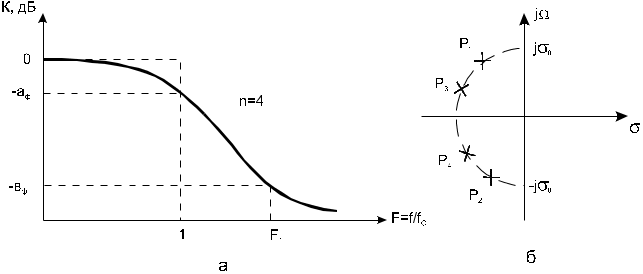
Риc.2. Аппроксимация АЧХ по Баттерворту
Порядок n аппроксимирующей функции (1) определяется по формуле

(2)

Полюсы передаточной функции располагаются и левой комплексной полуплоскости на полуокружности симметрично относительно действительной оси (рис.2,б). Их координаты рассчитываются с помощью выражения

i= , (3)

где _0–радиус полуокружности,

(4)

5. Каскадная реализация фильтра по передаточной функции K(p)
Реализация передаточных функций, обеспечивающих необходимую АЧХ , чаще всего осуществляется по методу каскадно-развязанного включения звеньев 1-го и 2-го порядков. При такой реализации передаточная функция должна быть представлена в виде произведения сомножителей 1-го и 2-го порядка K

---

Смотрите также файлы

• Перманганотометрия.rtf

• Кафедра Физики отчет по лабораторной работе 12 по дисциплине Физика Тема Исследование внешнего фотоэффекта Выполнение.pdf

• Основные принципы, задачи и этапы медицинской реабилитации больных и детейинвалидов.pdf

• Начало научной деятельности учёного.doc

• Курсовая работа по дисциплине Теория и методика высших достижений Средства и методы спортивной тренировки в подготовке спортсмена в лыжных гонках.doc