Файл: Национальный технический университет украины киевский политехнический институт кафедра систем автоматизированного проектирования.doc
Добавлен: 06.12.2023
Просмотров: 75
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i(p):
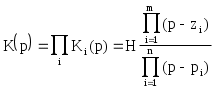(5)
Рис.3. Каскадное соединение звеньев
Каждый из сомножителей Ki в выражении (5) реализуется соответствующим звеном. Если звенья не влияют друг на друга. то схема обладает требуемой передаточной функцией n-го порядка.
Передаточную функцию K(p) можно разложить на сомножители, используя различные комбинации постоянных множителей Hi, нулей и полюсов. Вещественные полюса образуют звенья 1-го порядка с передаточной функцией
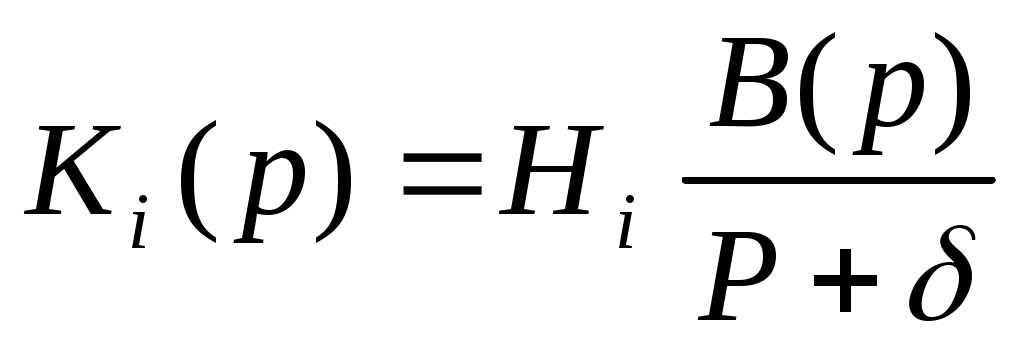, (6)
где B(p)–полином первой степени или единица;–постоянное число.
Комплексно-сопряженные полюсы образуют звенья 2-го порядка с передаточной функцией
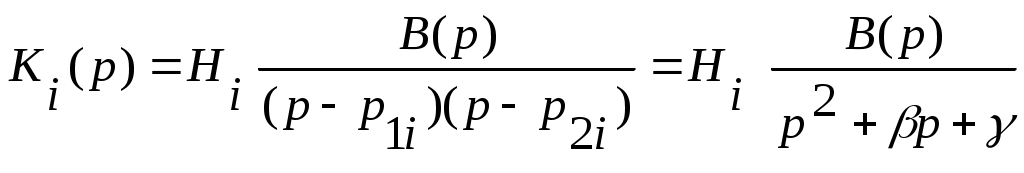, (7)
где В(р)–полином второй или меньшей степени;
и - постоянные коэффициенты.
Для фильтра нижних частот полином В(р) представляет собой единицу.
Для четного порядка n>2 каскадная схема содержит n/2 звеньев второго порядка, каждое с передаточной функцией типа (7). Если порядок n>2 является нечетным, то схема содержит (n-1)/2 звеньев второго порядка с передаточными функциями типа (7) и одно звено первого, порядка с передаточной функцией типа (6).
Для звеньев второго порядка, описываемых функцией (7), определим:
собственную частоту
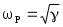(8)
и добротность
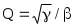(9)
Для обеспечения коэффициента передачи фильтра в полосе пропускания равного единице (0 дБ) необходимо соблюдать условие
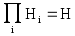(10)
Так как операционные усилители обладают большим входным и малым выходным сопротивлениями, то звенья, построенные с их применением, практически не влияют друг на друга.
Для фильтров нижних частот нечетного порядка одно звено должно обладать передаточной функцией первого порядка.
Звено ФНЧ первого порядка должно реализовывать передаточную функцию вида:
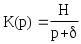(11)
Для реализации звена первого порядка можно использовать инвертирующий усилитель. На рис.4 изображена схема звена ФНЧ первого порядка с инвертирующим операционным усилителем. Передаточная функция такого звена имеет вид
(12)
Сопоставляя формулы (11) и (12), получаем расчетные соотношения (при выбранном нормированном значении емкости С)
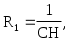
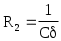
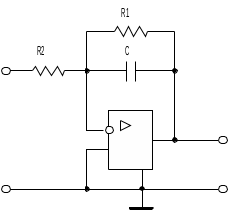
Рис.4. Звено ФНЧ первого порядка с инвертирующим ОУ
Для звена фильтра нижних частот второго порядка типовая передаточная функция имеет вид
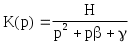(13)
На рис.5 изображено звено второго порядка, собранное по схеме с многопетлевой обратной связью (МОС). Эта схема реализует передаточную функцию с инвертирующим коэффициентом усиления (К<0) и параметрами
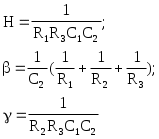
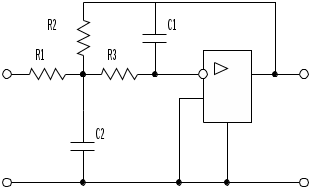
Рис.5. Звено ФНЧ второго порядка с МОС
Выбрав значения С1 и С2 можно рассчитать сопротивления:
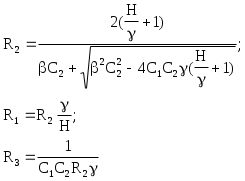
Значения емкостей С1 и С2 должны быть нормированными и в результате расчета давать положительное значение сопротивления R2. Это условие выполняется, если
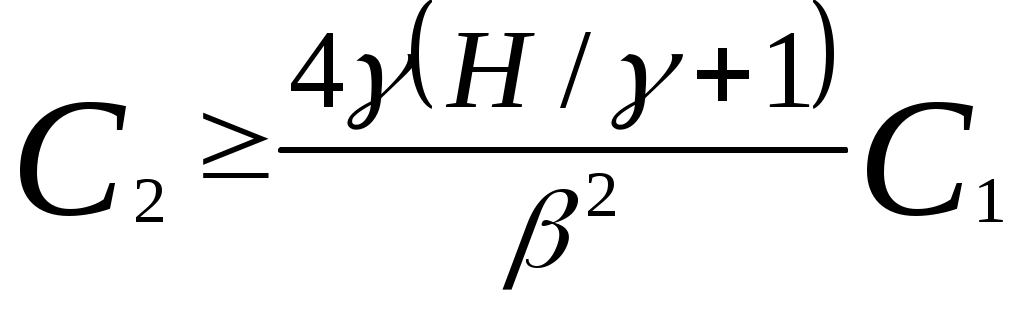
Схему с МОС целесообразно применять при добротностях, не превышающих 10.
При реализации звеньев второго порядка с добротностями выше 10 нужно применять более сложные схемы, например, так называемую биквадратную схему (рис.6). Такая схема реализует значения добротности вплоть до 100. Биквадратное звено ФНЧ реализует передаточную функцию (13) при неинвертирующем коэффициенте усиления и параметрах
H=1/R1R4
C12; =1/R2C1; =1/R3R4C12.
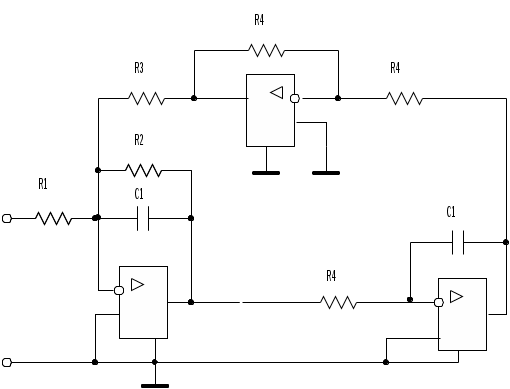
Рис.6. Биквадратное звено ФНЧ второго порядка
Значения сопротивлений определяются из следующих соотношений:
R1=1/HC12R4; R2=1/C1; R3=1/R4C12,
где С1 и R4 выбираются. Если значение С1 выбрано близким к 10, то приемлемое значение R4=1/C1.
Тогда получаем: R1=R4/H; R2=R4/; R3=R4/.
6. Денормирование электрических величин
После реализации передаточной функции с помощью звеньев первого и второго порядка для получения реальных значений сопротивлений входящих в эти звенья компонентов необходимо параметры R и L умножить, а С - разделить на R0.
Для перехода от нормированной циклической частоты к требуемому частотному диапазону, необходимо нормированные величины Lн и Cн разделить на 0, т.е.
L’H = LH /0
C’H = CH /0 ( 14 )
R’н = Rн.
Теперь нужно денормировать значения сопротивлений
L = L’H R0
C= C’H / R0 ( 15 )
R= R’нR0.
Таким образом, если нормирующими коэффициентами являются R0 и f0, а Rн, Lн и Сн представляют собой нормированные значения параметров пассивных компонентов, полученных в результате синтеза цепи, то их действительные значения после восстановления уровня (денормирования) сопротивлений и частоты на основании выражений (1) и (2) составят:
R=RHR0; C=CH/(R0 2f0 ); L=LHR0/(2f0); ( 16 )
При денормировании значений параметров компонентов величину R0 следует выбирать таким образом, чтобы значения R, C и L, рассчитанные с помощью формул (3), в рабочей области частот удовлетворяли условиям: Rвх>>R>>Rвых; Rвх>>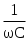
>>Rвых; Rвх>>L>>Rвых, где Rвх, Rвых - соответственно входные и выходные сопротивления используемых активных усилительных элементов (например, операционных усилителей).
7. Расчет ненормированной АЧХ фильтра
Согласно выражению (5) передаточная функция фильтра есть произведение передаточных функций его звеньев (при условии отсутствия их взаимного влияния друг на друга)
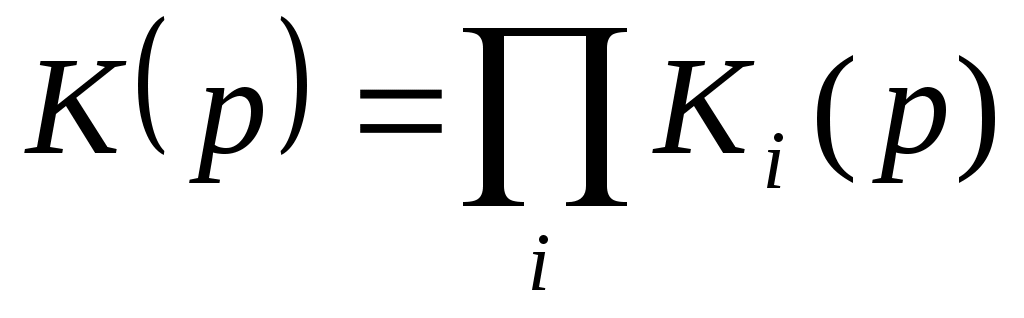
Таким образом, передаточная функция представлена в виде произведения сомножителей 1-го и 2-го порядка Ki(p), каждый из которых реализуется соответствующим звеном.
Звено первого порядка имеет передаточную фунцию вида
Для звена первого порядка, реализованного по схеме с инвертирующим ОУ,
H=1/R1C;
=1/R2C;
Звено второго порядка имеет передаточную фунцию вида
,
где параметры H,, определяются исходя из номиналов компонентов, входящих в конкретное звено.
Для звена второго порядка, реализованного по схеме с многопетлевой обратной связью (МОС)
Для звена второго порядка, реализованного по биквадратной схеме:
H=1/R1R4C12; =1/R2C1; =1/R3R4C12.
Таким образом, определив передаточную каждого звена и перемножив эти функции, получим передаточную функцию фильтра.
Осуществив подстановку
p = j 2f
и взяв модуль комплексной передаточной функции K(p), получим ненормированную АЧХ фильтра :
8. Описание программы , реализующей методику расчета
Программа, реализующая приведенную выше методику расчета, написана на языке Паскаль (для компилятора Boland Pascal 7.0) и предназначена для автоматизированного проектирования фильтров нижних частот с использованием максимально плоской аппроксимации амплитудно-частотной характеристики (аппроксимации Баттерворта). Листинг программы приведен в приложении П1. Программа позволяет рассчитать активный RC фильтр нижних частот до 50-го порядка. Программа также формирует файл протокола расчета filter.txt; файл filter.tab, содержащий результат табулирования АЧХ спроектированного фильтра, а также файл filter.atd, содержащий задание на моделирование фильтра и анализ его частотных характеристик в системе ALLTED.
После запуска программы на экране появляется заставка. После нажатия клавиши Enter программа запрашивает у пользователя параметры проектируемого фильтра: частоту среза, минимальную неравномерность коэффициента передачи в полосе пропускания, граничную частоту полосы задерживания и минимальное затухание коэффициента передачи в полосе задерживания. В случае ввода некорректного набора исходных данных программа выводит сообщение об ошибке и ее характере, после нажатия клавиши Enter программа повторно запрашивает у пользователя параметры фильтра. В случае, если введенные параметры корректны, то после нажатия клавиши Enter программа производит расчет фильтра. Если в процессе расчета будет получен порядок фильтра , превышающий установленный максимально допустимый (50), то выдается соответствующее сообщение и работа программы прекращается.
После завершения расчета на экране появляется информация о параметрах спроектированного фильтра, его порядок, количество звеньев, и их порядок, добротность, тип схемной реализации и номиналы компонентов в этих реализациях. Для реализации звеньев первого порядка используется схема на инвертирующем ОУ. Для звеньев второго порядка с добротностью <10 – схема с многопетлевой обратной связью; с добротностью <10 – биквадратная схема.
После просмотра результатов расчета нажимают Enter и программа выводит на экран график логарифмической АЧХ спроектированного фильтра (дБ). При нажатии любой клавиши работа программы завершается.
9. Расчет схемы фильтра с помощью разработанной программы
С помощью разработанной программы, описание которой приведено в предыдущем пункте, был проведен расчет схемы фильтра нижних частот в соответствии с вариантом задания на курсовую работу. Результаты расчета схемы фильтра приведены в приложении П2. Фильтр имеет порядок 8 и требует для своей реализации четыре звена второго порядка, построенных по схеме с многопетлевой обратной связью. График логарифмической АЧХ схемы фильтра, построенный разработанной программой, приводится в приложении П3. В приложении П4 приводится листинг файла filter.txt, содержащего протокол расчета схемы фильтра. Листинг сгенерированного программой файла filter.atd, содержащего задание на моделирование с помощью пакета ALLTED, приводится в приложении П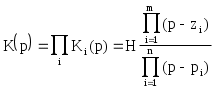5.
(5) Рис.3. Каскадное соединение звеньев
Каждый из сомножителей Ki в выражении (5) реализуется соответствующим звеном. Если звенья не влияют друг на друга. то схема обладает требуемой передаточной функцией n-го порядка.
Передаточную функцию K(p) можно разложить на сомножители, используя различные комбинации постоянных множителей Hi, нулей и полюсов. Вещественные полюса образуют звенья 1-го порядка с передаточной функцией
, (6)где B(p)–полином первой степени или единица;–постоянное число.
Комплексно-сопряженные полюсы образуют звенья 2-го порядка с передаточной функцией
, (7)где В(р)–полином второй или меньшей степени;
и - постоянные коэффициенты.
Для фильтра нижних частот полином В(р) представляет собой единицу.
Для четного порядка n>2 каскадная схема содержит n/2 звеньев второго порядка, каждое с передаточной функцией типа (7). Если порядок n>2 является нечетным, то схема содержит (n-1)/2 звеньев второго порядка с передаточными функциями типа (7) и одно звено первого, порядка с передаточной функцией типа (6).
Для звеньев второго порядка, описываемых функцией (7), определим:
собственную частоту
(8) и добротность
(9)Для обеспечения коэффициента передачи фильтра в полосе пропускания равного единице (0 дБ) необходимо соблюдать условие
(10)Так как операционные усилители обладают большим входным и малым выходным сопротивлениями, то звенья, построенные с их применением, практически не влияют друг на друга.
Реализация передаточных функций первого порядка
для фильтров нижних частот
Для фильтров нижних частот нечетного порядка одно звено должно обладать передаточной функцией первого порядка.
Звено ФНЧ первого порядка должно реализовывать передаточную функцию вида:
(11)Для реализации звена первого порядка можно использовать инвертирующий усилитель. На рис.4 изображена схема звена ФНЧ первого порядка с инвертирующим операционным усилителем. Передаточная функция такого звена имеет вид
(12)Сопоставляя формулы (11) и (12), получаем расчетные соотношения (при выбранном нормированном значении емкости С)
Рис.4. Звено ФНЧ первого порядка с инвертирующим ОУ
Реализация передаточных функций второго порядка
для фильтров нижних частот
Для звена фильтра нижних частот второго порядка типовая передаточная функция имеет вид
(13)На рис.5 изображено звено второго порядка, собранное по схеме с многопетлевой обратной связью (МОС). Эта схема реализует передаточную функцию с инвертирующим коэффициентом усиления (К<0) и параметрами
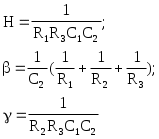
Рис.5. Звено ФНЧ второго порядка с МОС
Выбрав значения С1 и С2 можно рассчитать сопротивления:
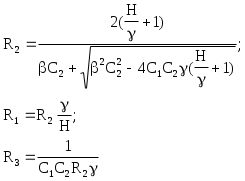
Значения емкостей С1 и С2 должны быть нормированными и в результате расчета давать положительное значение сопротивления R2. Это условие выполняется, если
Схему с МОС целесообразно применять при добротностях, не превышающих 10.
При реализации звеньев второго порядка с добротностями выше 10 нужно применять более сложные схемы, например, так называемую биквадратную схему (рис.6). Такая схема реализует значения добротности вплоть до 100. Биквадратное звено ФНЧ реализует передаточную функцию (13) при неинвертирующем коэффициенте усиления и параметрах
H=1/R1R4
C12; =1/R2C1; =1/R3R4C12.
Рис.6. Биквадратное звено ФНЧ второго порядка
Значения сопротивлений определяются из следующих соотношений:
R1=1/HC12R4; R2=1/C1; R3=1/R4C12,
где С1 и R4 выбираются. Если значение С1 выбрано близким к 10, то приемлемое значение R4=1/C1.
Тогда получаем: R1=R4/H; R2=R4/; R3=R4/.
6. Денормирование электрических величин
После реализации передаточной функции с помощью звеньев первого и второго порядка для получения реальных значений сопротивлений входящих в эти звенья компонентов необходимо параметры R и L умножить, а С - разделить на R0.
Для перехода от нормированной циклической частоты к требуемому частотному диапазону, необходимо нормированные величины Lн и Cн разделить на 0, т.е.
L’H = LH /0
C’H = CH /0 ( 14 )
R’н = Rн.
Теперь нужно денормировать значения сопротивлений
L = L’H R0
C= C’H / R0 ( 15 )
R= R’нR0.
Таким образом, если нормирующими коэффициентами являются R0 и f0, а Rн, Lн и Сн представляют собой нормированные значения параметров пассивных компонентов, полученных в результате синтеза цепи, то их действительные значения после восстановления уровня (денормирования) сопротивлений и частоты на основании выражений (1) и (2) составят:
R=RHR0; C=CH/(R0 2f0 ); L=LHR0/(2f0); ( 16 )
При денормировании значений параметров компонентов величину R0 следует выбирать таким образом, чтобы значения R, C и L, рассчитанные с помощью формул (3), в рабочей области частот удовлетворяли условиям: Rвх>>R>>Rвых; Rвх>>
>>Rвых; Rвх>>L>>Rвых, где Rвх, Rвых - соответственно входные и выходные сопротивления используемых активных усилительных элементов (например, операционных усилителей). 7. Расчет ненормированной АЧХ фильтра
Согласно выражению (5) передаточная функция фильтра есть произведение передаточных функций его звеньев (при условии отсутствия их взаимного влияния друг на друга)
Таким образом, передаточная функция представлена в виде произведения сомножителей 1-го и 2-го порядка Ki(p), каждый из которых реализуется соответствующим звеном.
Звено первого порядка имеет передаточную фунцию вида
Для звена первого порядка, реализованного по схеме с инвертирующим ОУ,
H=1/R1C;
=1/R2C;
Звено второго порядка имеет передаточную фунцию вида
,где параметры H,, определяются исходя из номиналов компонентов, входящих в конкретное звено.
Для звена второго порядка, реализованного по схеме с многопетлевой обратной связью (МОС)
Для звена второго порядка, реализованного по биквадратной схеме:
H=1/R1R4C12; =1/R2C1; =1/R3R4C12.
Таким образом, определив передаточную каждого звена и перемножив эти функции, получим передаточную функцию фильтра.
Осуществив подстановку
p = j 2f
и взяв модуль комплексной передаточной функции K(p), получим ненормированную АЧХ фильтра :
A(f) = | K(j2f) |
8. Описание программы , реализующей методику расчета
Программа, реализующая приведенную выше методику расчета, написана на языке Паскаль (для компилятора Boland Pascal 7.0) и предназначена для автоматизированного проектирования фильтров нижних частот с использованием максимально плоской аппроксимации амплитудно-частотной характеристики (аппроксимации Баттерворта). Листинг программы приведен в приложении П1. Программа позволяет рассчитать активный RC фильтр нижних частот до 50-го порядка. Программа также формирует файл протокола расчета filter.txt; файл filter.tab, содержащий результат табулирования АЧХ спроектированного фильтра, а также файл filter.atd, содержащий задание на моделирование фильтра и анализ его частотных характеристик в системе ALLTED.
После запуска программы на экране появляется заставка. После нажатия клавиши Enter программа запрашивает у пользователя параметры проектируемого фильтра: частоту среза, минимальную неравномерность коэффициента передачи в полосе пропускания, граничную частоту полосы задерживания и минимальное затухание коэффициента передачи в полосе задерживания. В случае ввода некорректного набора исходных данных программа выводит сообщение об ошибке и ее характере, после нажатия клавиши Enter программа повторно запрашивает у пользователя параметры фильтра. В случае, если введенные параметры корректны, то после нажатия клавиши Enter программа производит расчет фильтра. Если в процессе расчета будет получен порядок фильтра , превышающий установленный максимально допустимый (50), то выдается соответствующее сообщение и работа программы прекращается.
После завершения расчета на экране появляется информация о параметрах спроектированного фильтра, его порядок, количество звеньев, и их порядок, добротность, тип схемной реализации и номиналы компонентов в этих реализациях. Для реализации звеньев первого порядка используется схема на инвертирующем ОУ. Для звеньев второго порядка с добротностью <10 – схема с многопетлевой обратной связью; с добротностью <10 – биквадратная схема.
После просмотра результатов расчета нажимают Enter и программа выводит на экран график логарифмической АЧХ спроектированного фильтра (дБ). При нажатии любой клавиши работа программы завершается.
9. Расчет схемы фильтра с помощью разработанной программы
С помощью разработанной программы, описание которой приведено в предыдущем пункте, был проведен расчет схемы фильтра нижних частот в соответствии с вариантом задания на курсовую работу. Результаты расчета схемы фильтра приведены в приложении П2. Фильтр имеет порядок 8 и требует для своей реализации четыре звена второго порядка, построенных по схеме с многопетлевой обратной связью. График логарифмической АЧХ схемы фильтра, построенный разработанной программой, приводится в приложении П3. В приложении П4 приводится листинг файла filter.txt, содержащего протокол расчета схемы фильтра. Листинг сгенерированного программой файла filter.atd, содержащего задание на моделирование с помощью пакета ALLTED, приводится в приложении П5.