Экзаменационные вопросы

1. Перечислите принципы управления и поясните их.

Ответ :

Принято классифицировать системы автоматического управления по ряду признаков, определяющих их отношение к тому или иному классу САУ.

Прежде всего принято разделять САУ по принципу управления. По этому признаку различают системы:

• 
  с разомкнутым циклом управления,
  
• 
  с управлением по возмущениям,
  
• 
  с управлением с обратной связью,
  
• 
  с комбинированным принципом управления.
  

В системах с разомкнутым циклом управления информация о действительном поведении объекта управления не используется для целей управления (рис. 1.1).

Системы с разомкнутым принципом управления оказываются эффективными лишь тогда, когда характеристики  ОУ достаточно стабильны и возмущающее воздействие F незначительно влияет на выходную величину Y.



Рис. 1.1

В системах с управлением по возмущениям в структуру разомкнутого управления добавляется еще один блок (рис. 1.2) – устройство измерения возмущений (ИВ), обеспечивающее дополнительное компенсационное воздействие на ОУ при значительных изменениях возмущающего воздействия F.



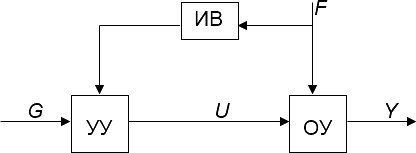
Рис. 1.2

В системах управления с обратной связью (рис. 1.3) информация о действительном поведении объекта управления снимается с выхода ОУ, обрабатывается в устройстве обратной связи (УОС) и подается в устройство сравнения (УС), где сравнивается с информацией о желаемом поведении объекта управления.



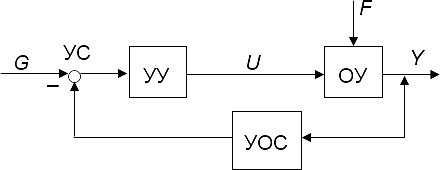
Рис. 1.3

Преимуществом систем управления с обратной связью является более высокая точность воспроизведения желаемого поведения ОУ, большая инвариантность по отношению к возмущающим воздействиям и меньшая зависимость от изменения характеристик ОУ или УУ.

В системах комбинированного управления сочетается принцип обратной связи с принципом прямого управления по внешним воздействиям: возмущающим (рис. 1.4, а) и управляющим (рис. 1.4, б).

---

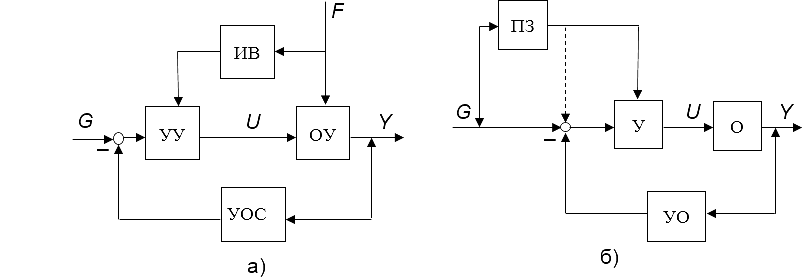
Рис. 1.4

В схеме рис. 1.4 б, ПЗ – преобразователь управляющего (задающего) воздействия. Системы с комбинированным принципом управления обеспечивают повышенную точность воспроизведения желаемого в технике управления.

2. Что представляет собой закон управления?

Ответ:

Законы управления. Типовые регуляторы

Закон управления - это алгоритм или функциональная зависимость, в соответствии с которыми регулятор формирует управляющее воздействие u(t). Эта зависимость может быть представлена в виде

u(t) = F(x, g, f), (8.1)

где F - некоторый оператор от отклонения x, задающего воздействия g и возмущающего воздействия f, а также от их производных и интегралов по времени.

Обычно выражение (8.1) может быть записано следующим образом:

u(t) = F₁(x) + F₂(g) + F₃(f). (8.2)

Здесь первое слагаемое соответствует управлению по отклонению, второе и третье - управлению по внешнему воздействию.

В зависимости от вида оператора F законы управления делятся на стандартные и специальные.

Стандартные законы управления - это универсальные законы, с помощью которых можно решать задачи автоматизации разнообразных технологических процессов и объектов.

Специальные законы управления - это законы, формируемые для решения конкретных задач.

Если для формирования управляющего воздействия u(t) используются только линейные математические операции, то такой закон управления называется линейным, в противном случае - нелинейным.

Линейный стандартный закон управления имеет следующий вид:



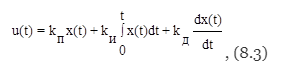
где первое слагаемое является пропорциональной, второе - интегральной, третье - дифференциальной составляющими закона, а коэффициенты k_П, k_И и k_Д определяют вклад каждой из составляющих в формируемое управляющее воздействие.

Интегральная составляющая закона управления вводится для повышения точности, а дифференциальная - для повышения быстродействия работы системы.

Регулятор, формирующий управляющее воздействие в соответствии с (8.3), имеет передаточную функцию



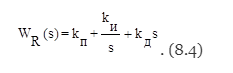
Структурная схема линейного стандартного регулятора приведена на рис.8.1.

Настройка такого регулятора заключается в задании значений коэффициентов k

---

_П, k_И, k_Д таким образом, чтобы удовлетворить требованиям качества управления в соответствии с выбранными критериями качества.



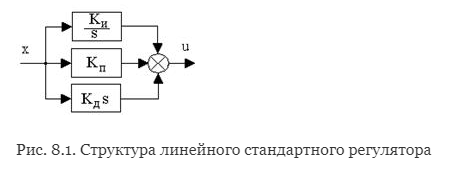
На практике широкое распространение получили типовые или промышленные регуляторы, представляющие собой универсальные автоматические устройства, легко приспосабливаемые для автоматизации разнообразных технологических процессов и объектов. При этом объект управления, как правило, является звеном статического типа, т.е. W_ОУ(0)=k_ОУ, где k_ОУ - коэффициент передачи объекта управления. Типовые регуляторы реализуют типовые законы управления, являющиеся частными случаями линейного стандартного закона управления, и классифицируются следующим образом.

П-регуляторы. Реализуют П-закон или пропорциональный закон управления

u(t) = k_П x(t).

Передаточная функция П-регулятора

W_R(s) = k_П.

Пропорциональное управление позволяет уменьшить установившуюся ошибку в объекте в (1+k) раз, где k = k_П´k_ОУ - коэффициент передачи разомкнутой системы. Регулирование в этом случае получается статическим, так как при любом конечном значении коэффициента передачи разомкнутой системы установившаяся ошибка будет отличной от нуля.



При интегральном управлении получается система, астатическая по отношению к задающему воздействию. Повышение степени астатизма приводит к увеличению установившейся точности системы, но одновременно снижает ее быстродействие, а также приводит к ухудшению устойчивости. Снижение быстродействия объясняется тем, что в первый момент времени при появлении ошибки управляющее воздействие равняется нулю и только затем начинается его рост. В системе пропорционального управления рост управляющего воздействия в первые моменты времени происходит более интенсивно, так как наличие ошибки сразу дает появление управляющего воздействия, в то время как в системе интегрального управления должно пройти некоторое время.



Пропорционально-интегральное (изодромное) управление сочетает в себе высокую точность интегрального управления (астатизм) с большим быстродействием пропорционального управления. В первые моменты времени при появлении ошибки система с ПИ-регулятором работает как система пропорционального регулирования, а в дальнейшем начинает работать как система интегрального управления.

---

Пропорционально-дифференциальное управление применяются для повышения быстродействия работы системы.

Регулирование по производной не имеет самостоятельного значения, так как в установившемся состоянии производная от ошибки равна нулю и управление прекращается. Однако она играет большую роль в переходных процессах, потому что позволяет учитывать тенденцию к росту или уменьшению ошибки. В результате увеличивается скорость реакции системы, повышается быстродействие, снижается ошибка в динамике.

ПИД-регуляторы. Реализуют ПИД-закон или пропорционально-интегрально-дифференциальный закон управления, соответствующий линейному стандартному закону вида (8.3).

ПИД-регулятор, представляющий собой астатический изодромный регулятор с предвидением, обеспечивает повышенную точность и повышенное быстродействие системы.

3. Каково назначение регулятора в системе?

Ответ:

Регулятор, или управляющее устройство, — в теории автоматического управления это устройство, которое следит за состоянием объекта управления как системы и вырабатывает для неё управляющие сигналы. Регулятор следит за изменением некоторых параметров объекта управления (непосредственно либо с помощью наблюдателей) и реагируют на их изменение с помощью некоторых воздействий в соответствии с заданным качеством управления. Регуляторы в подавляющем большинстве работают по принципу отрицательной обратной связи с целью компенсировать внешние возмущения, действующие на объект управления, и отработать заданный извне или заложенный в системе закон управления.  Основным назначением регулятора является компенсация основных инерционностей контура;

4. По каким признакам классифицируются системы управления?

Ответ:

1)  Прежде всего принято разделять САУ по принципу управления. По этому признаку различают системы:

• 
  с разомкнутым циклом управления,
  
• 
  с управлением по возмущениям,
  
• 
  с управлением с обратной связью,
  
• 
  с комбинированным принципом управления.
  

2) Вторым важным признаком классификации САУ является тип управления. По типу управления различают шесть основных классов систем управления:

---

• 
  системы стабилизации;
  
• 
  системы  программного управления;
  
• 
  следящие системы;
  
• 
  системы оптимального управления;
  
• 
  системы экстремального управления;
  
• 
  системы адаптивного управления.
  

3) Третьим существенным признаком классификации САУ  является характер сигналов управления, используемых в системах управления. По этому признаку все системы разделяются на:

• 
  непрерывные
  
• 
  релейные,
  
• 
  дискретные.
  

Дискретной системой называется такая САУ, в которой имеет место прерывистый характер передачи информации управления. Такой характер сигналов управления  может быть обусловлен включением в систему импульсных или цифровых устройств. В связи с этими  все дискретные системы разделяются на две большие группы:

• 
  импульсные САУ;
  
• 
  цифровые САУ.
  

5. Дайте классификацию систем по виду задающего воздействия.

Ответ:

По виду задающего воздействия замкнутые САУ бывают системами следящими, стабилизации и программного управления.

Следящей называется САУ, предназначенная для воспроизведения произвольного задающего воздействия g(t), например, следящая система дистанционного управления орудием.

Если функция g(t) - заранее известная функция времени (заданная программа изменения температуры в термокамере), то соответствующая следящая система называется системой программного управления.

Если функция g(t) = const, то такая следящая система называется системой стабилизации

6. Назовите необходимые и достаточные условия линейности систем.

Ответ:

Линейные системы - это системы, которые описываются линейными уравнениями (алгебраическими и дифференциальными или разностными). Если система описывается обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами, то систему называют обыкновенной линейной системой. Закон управления линейной системы формируется линейными математическими операциями.

Необходимые и достаточные условия линейности системы:

1) в установившемся процессе выходной сигнал должен в некотором масштабе повторять входной сигнал;

2) сумме двух входных воздействий должна соответствовать сумма соответствующих выходных переменных.

К линейным системам применим принцип суперпозиции, в соответствии с которым выходной сигнал линейной системы на любое произвольное входное воздействие можно определить через ее реакцию на определенное элементарное воздействие.

---

Смотрите также файлы

• Студент (ка) учебной группы .docx

• Топология Таблица адресации.docx

• Вопросы для подготовки к экзамену Функциональноструктурная организация информационных систем на архитектуре клиентсервер.docx

• Внешняя политика Это деятельность на международной арене, регулирующая взаимоотношения с другими государствами и народами.docx

• Жасспірімдерді нашаорлыа атынасы сауалнамасы.docx