Файл: Сборник задач по высшей математике РостовнаДону 2002 г. Составитель Л. В. Сахарова удк 517 с 221.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 69
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство транспорта РФ
Филиал Новороссийской государственной
морской академии
в г. Ростове-на-Дону
Введение в анализ. Дифференциальное исчисление функций одной переменной
Сборник задач по высшей математике
Ростов-на-Дону
2002 г.
Составитель Л.В. Сахарова
УДК 517
С 221
Введение в анализ. Дифференциальное исчисление функций одной переменной: Сборник задач по высшей математике. Ростов-на-Дону: Типография ООО "ВУД", 2002.- с.
Пособие предназначено для проведения занятий по курсу высшей математики и организации самостоятельной работы курсантов. Может быть использовано для составления вариантов типового расчётного задания.
Печатается по решению общенаучной кафедры филиала НГМА в г. Ростове-на-Дону
Рецензент: начальник общенаучной кафедры филиала НГМА,
доцент, к.ф.-м.н. Н.Ю.Сафонцева
Типография ООО "ВУД", 2002
§1. Функциональная зависимость
1.1. Дано:
1.2. Дано:
1.3. Дано:
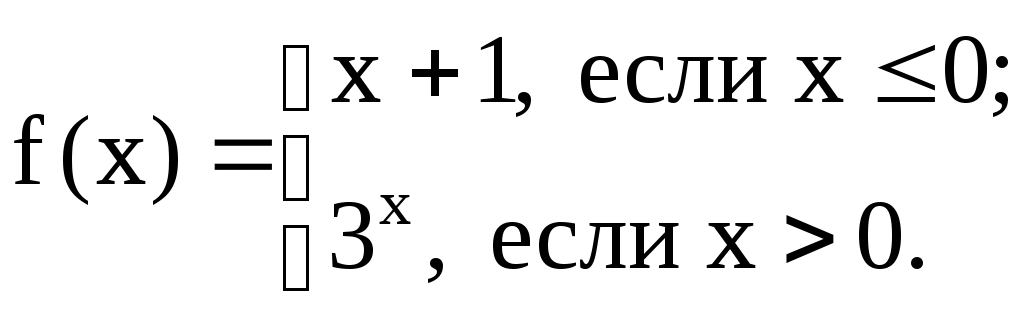 . Найти: f(–1); f(1); f(0);
. Найти: f(–1); f(1); f(0); 1.4. Дано:
Найти:
1.5. Доказать, что функция
.
1.6. Доказать, что функция
1.7. Дано:
1)
2)
1.8. Дано:
1.9. Дано:
1.10. Дано:
1.11. Найти области определения следующих функций:
1)
3)
5)
7)
9)
11)
13)
; 14)
15)
1.12. Записать в явном виде функцию y, заданную неявно:
1)
3)
5)
7)
1.13. Из уравнений, параметрически задающих функцию, исключить параметр:
1)
3)
5)
1.14. Выяснить, какие из следующих функций являются чётными, нечётными, какие не являются ни чётными, ни нечётными:
1)
;
3)
5)
7)
9)
11)
1.15. Для данных функций найти им обратные:
1)
3)
5)
7)
9)
11)
1.16. Какие из следующих функций являются периодическими:
1)
3)
5)
; 6)
7)
9)
§2. Пределы
В задачах 2.1–2.64 вычислить пределы:
2.1.
2.3.
2.5.
2.7.
2.9.
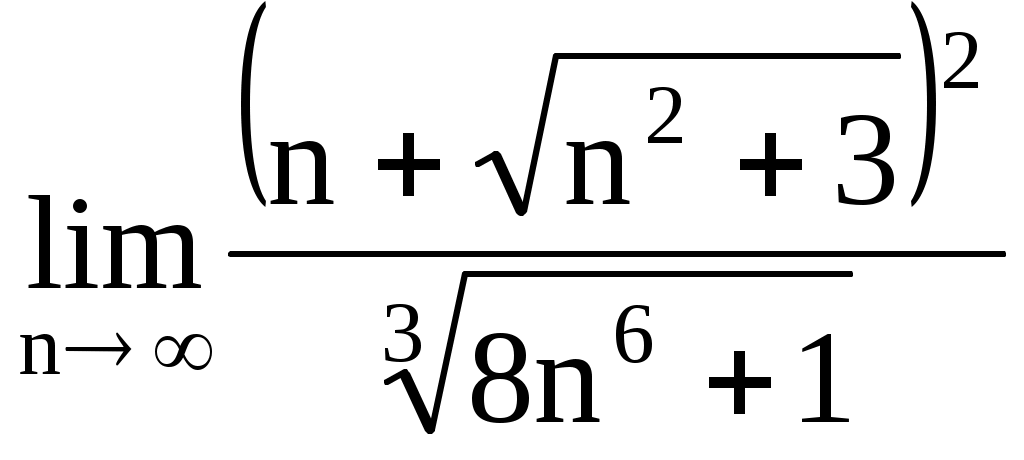 .
.2.11.
2.13.
2.15.
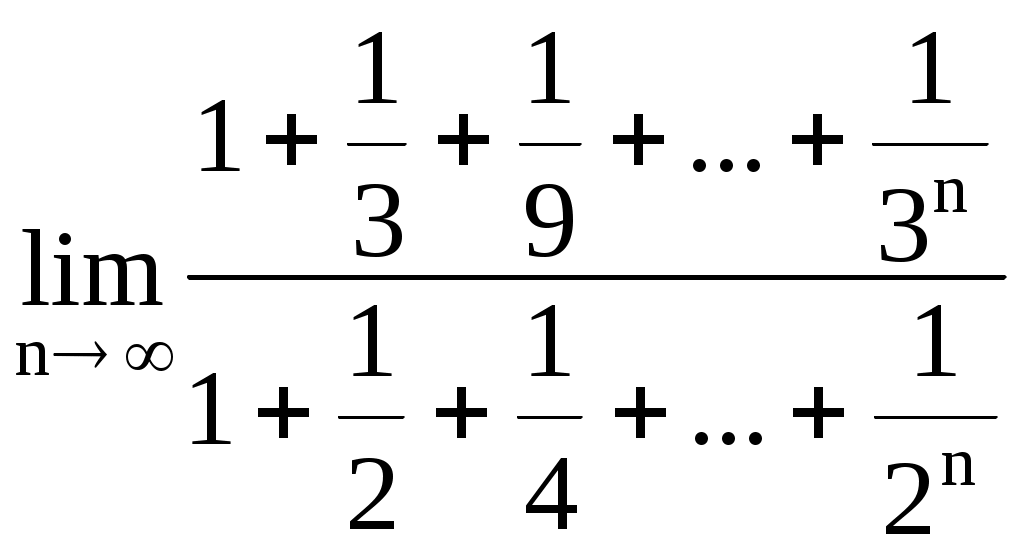 . 2.16.
. 2.16. 2.17.
2.19.
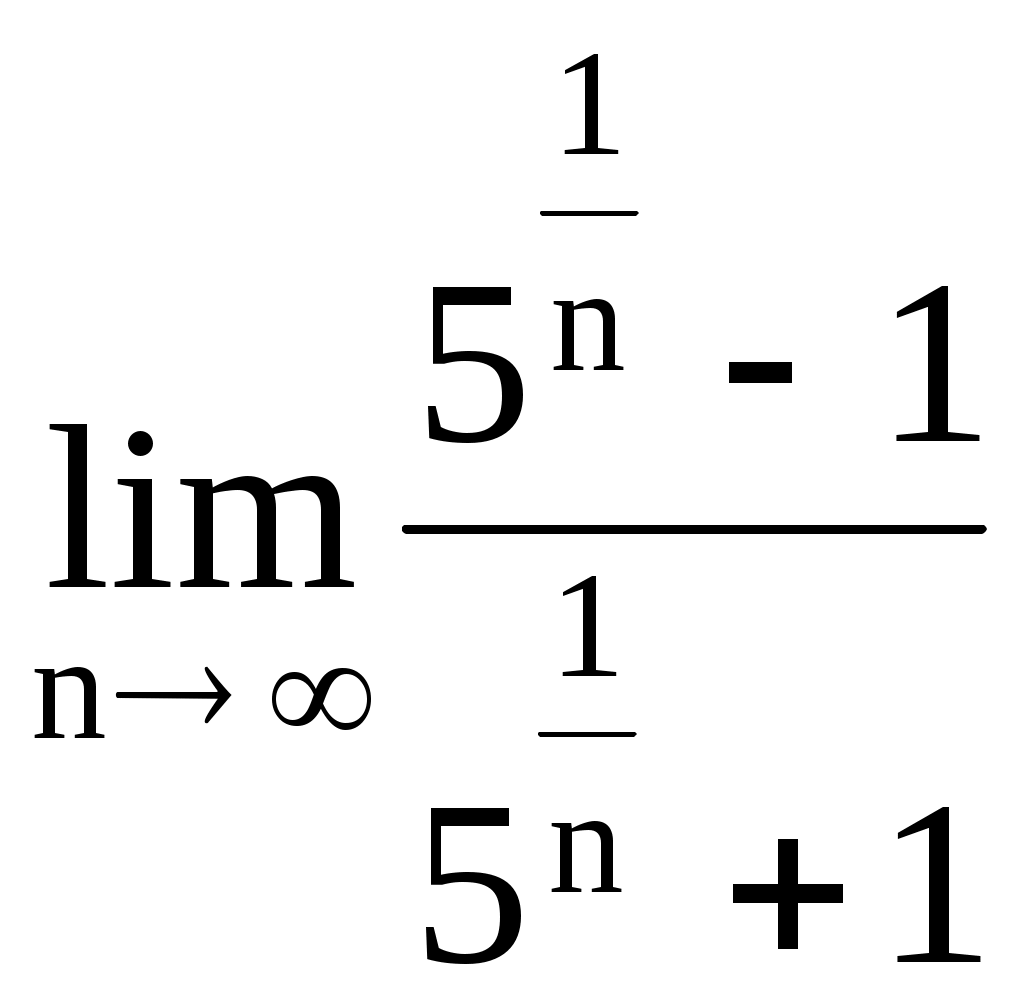 .
.2.21.