Файл: Сборник задач по высшей математике РостовнаДону 2002 г. Составитель Л. В. Сахарова удк 517 с 221.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 73
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
4)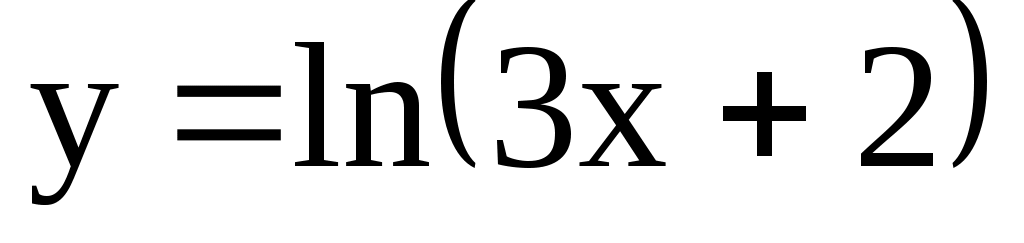 ; 5)
; 5) 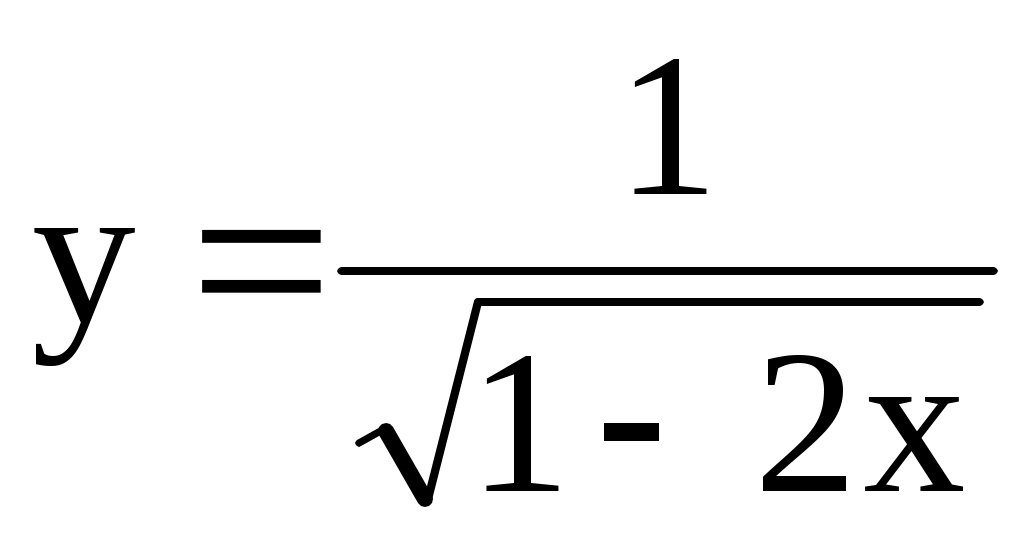 ; 6)
; 6) 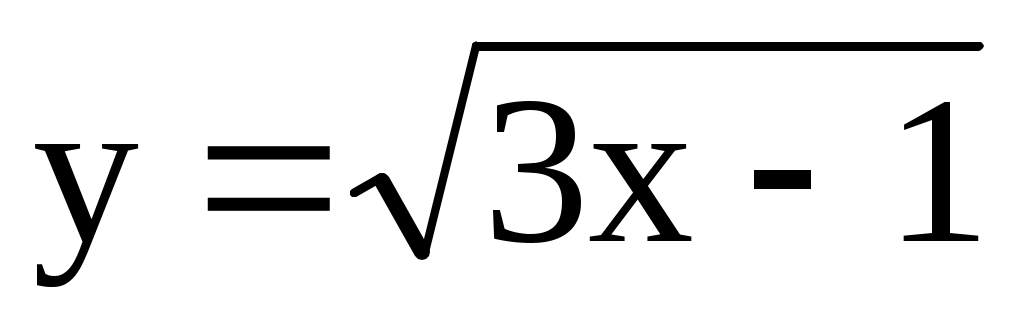 .
.
Функции, заданные в неявном виде
4.136.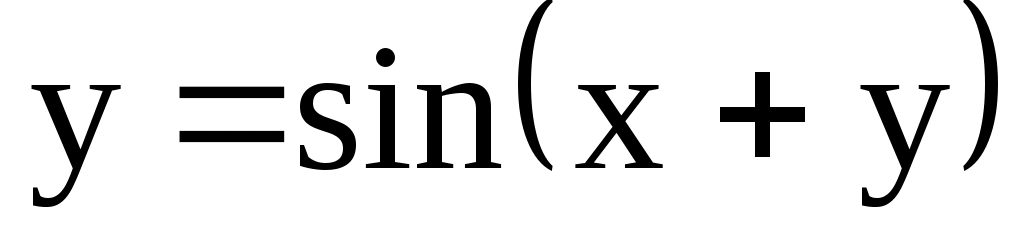 ;
; 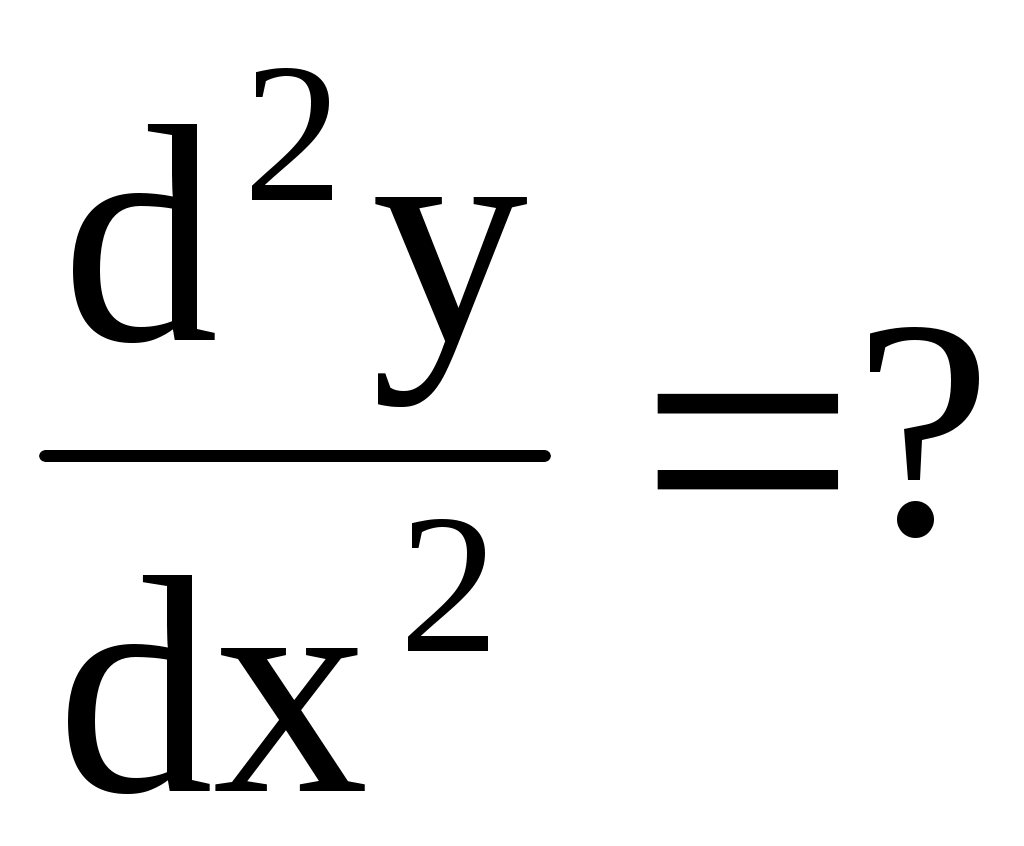 .
.
4.137.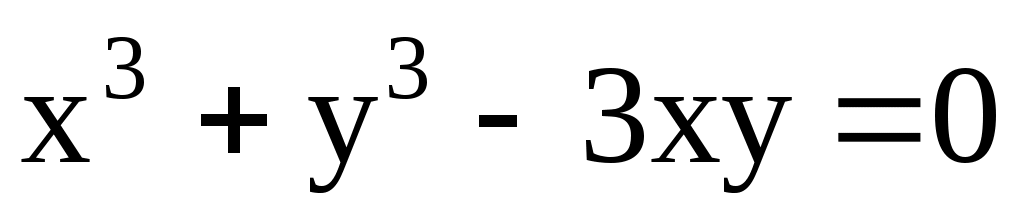 ;
; 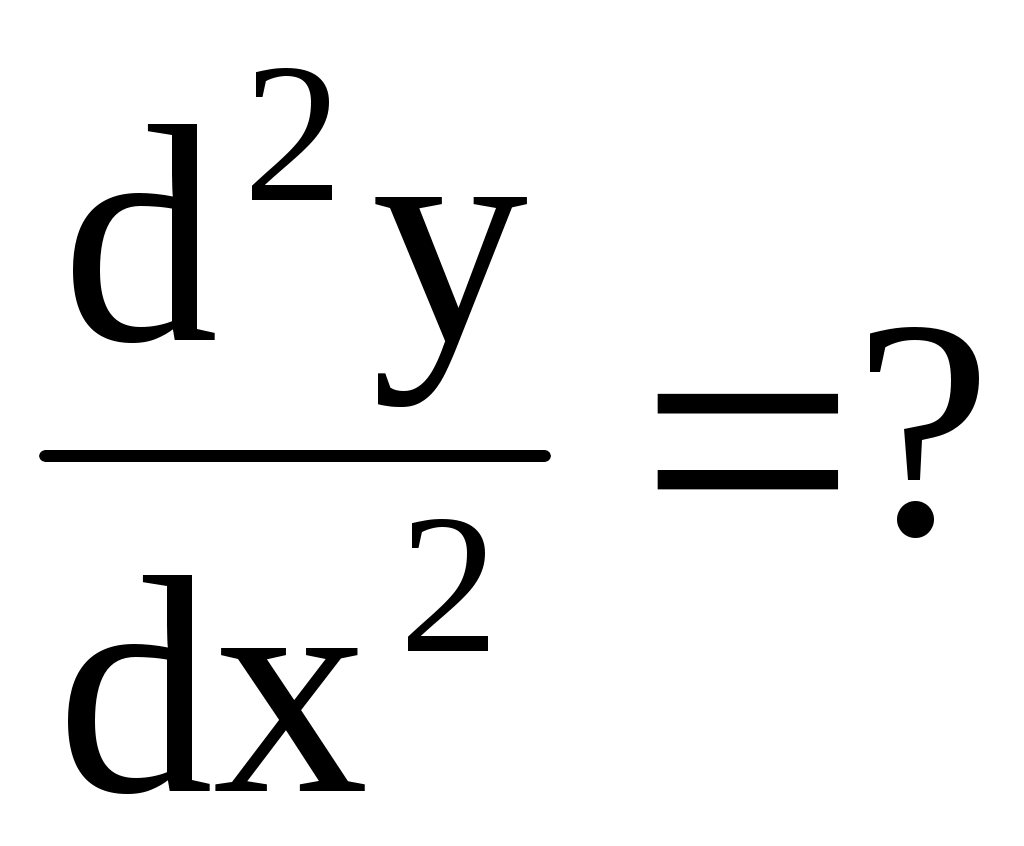 .
.
4.138.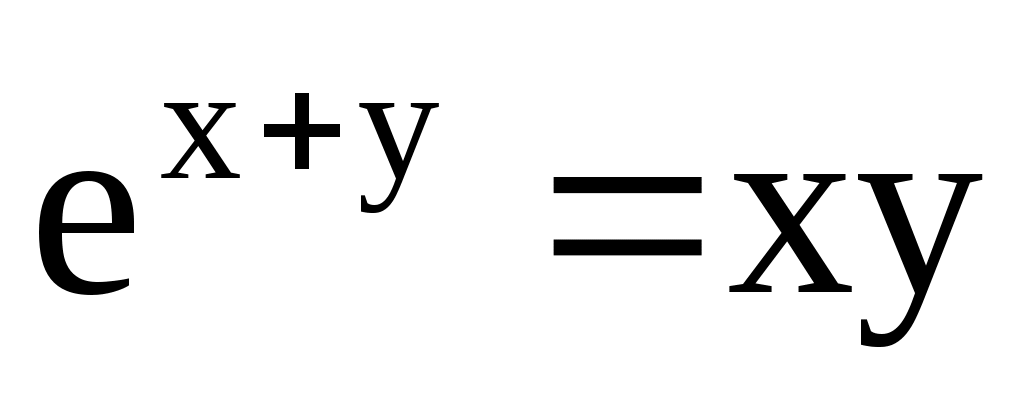 ;
; 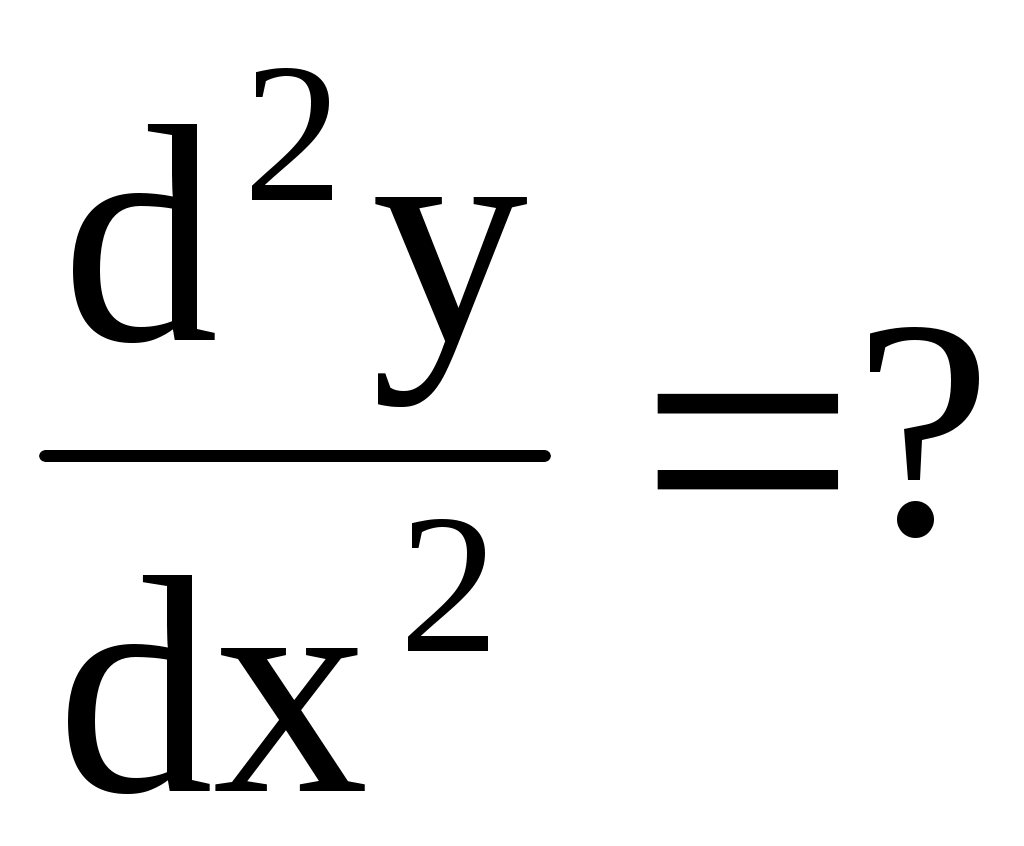 .
.
4.139.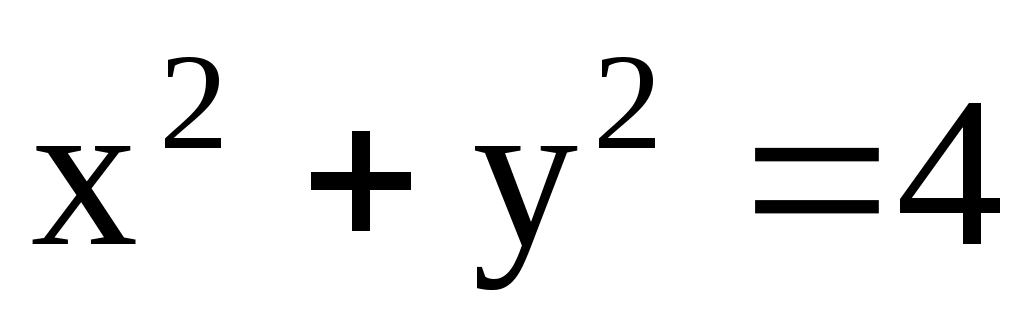 ;
; 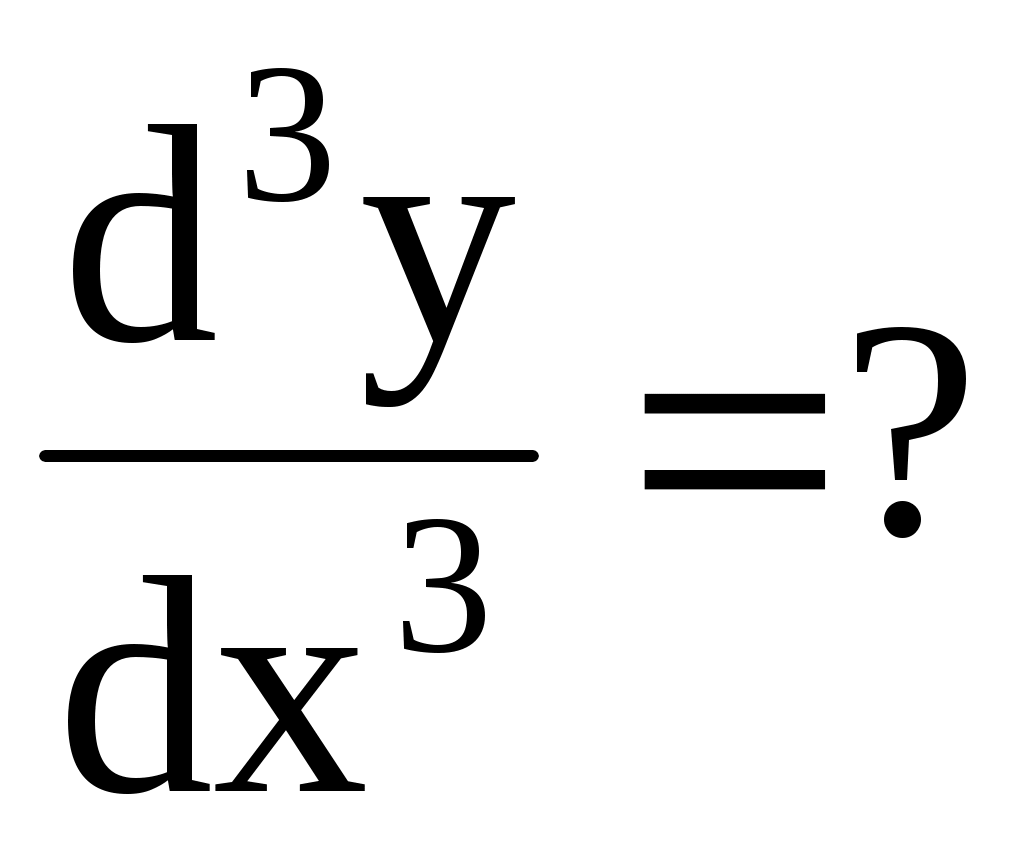 .
.
4.140.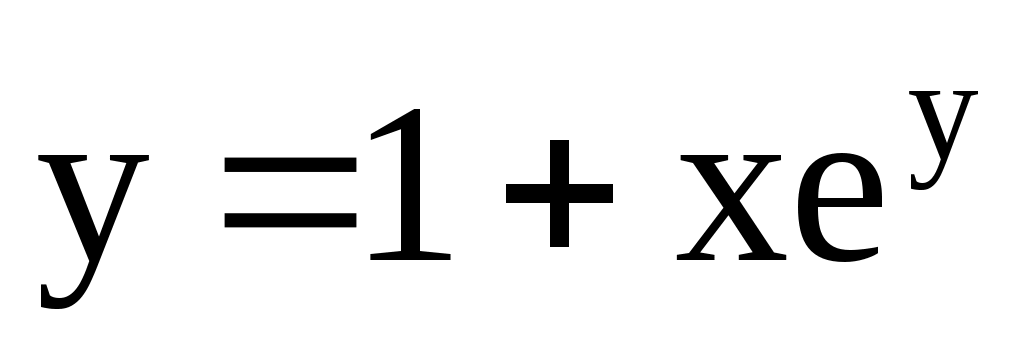 ;
; 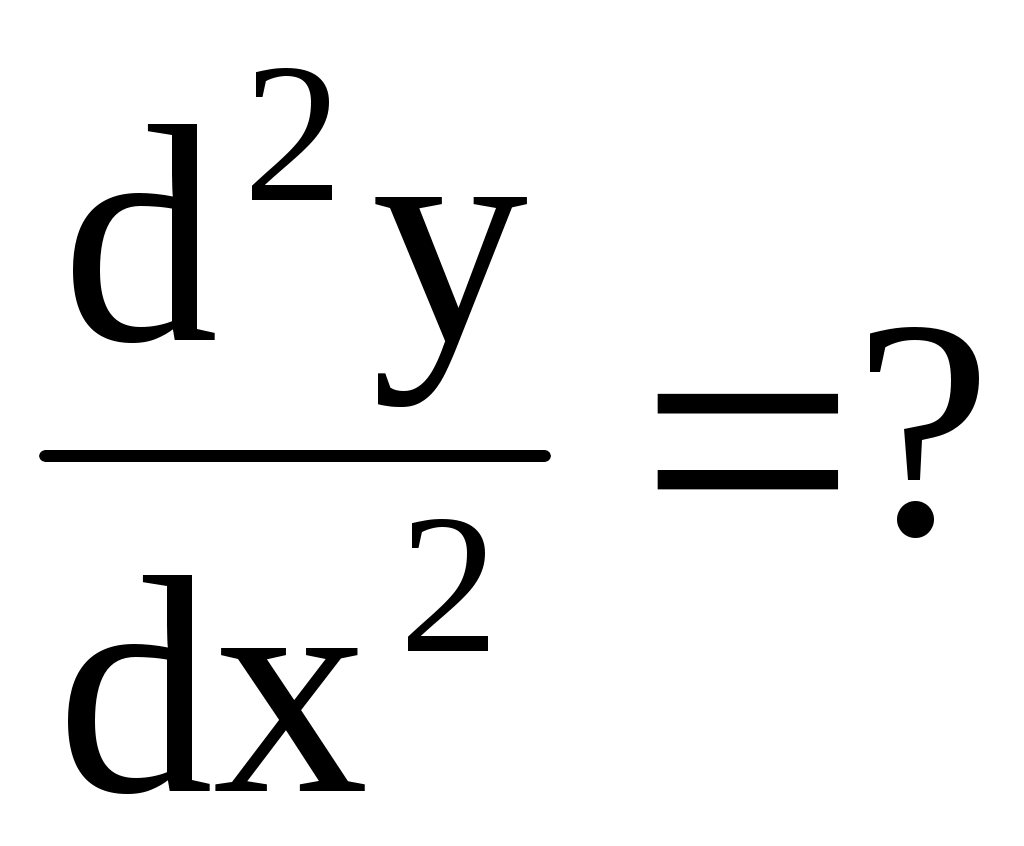 .
.
В задачах 4.141–4.151 для функций, заданных параметрически, найти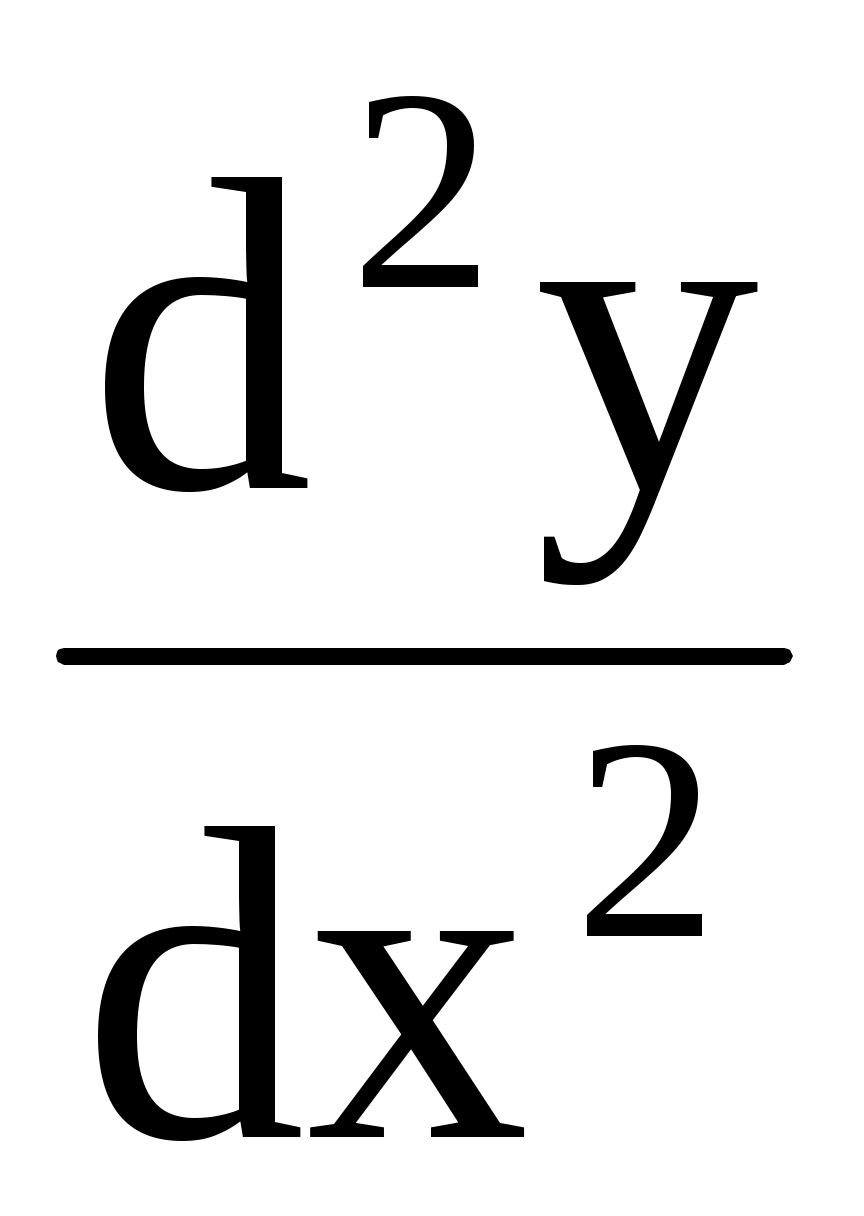 :
:
4.141. ;
; 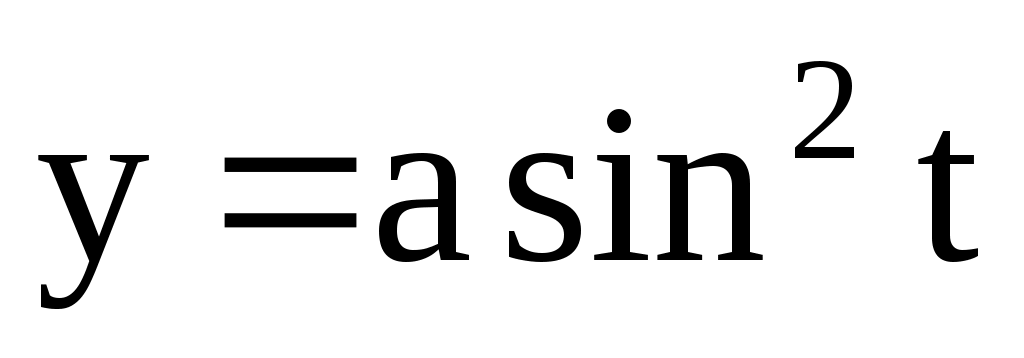 . 4.142.
. 4.142. 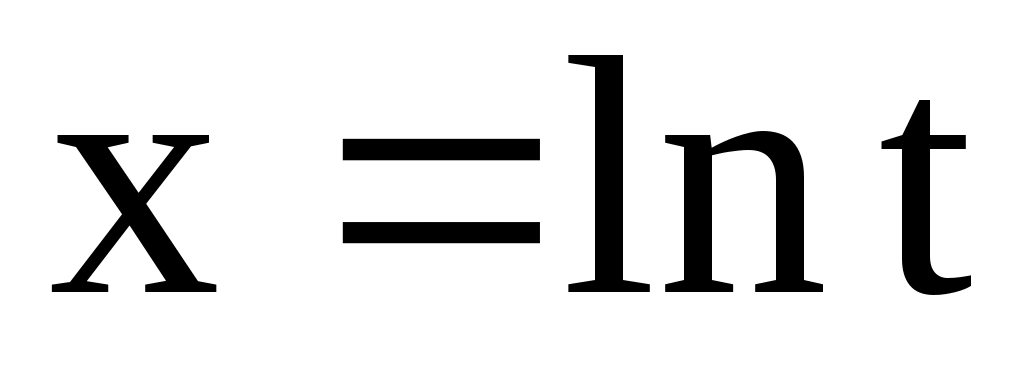 ;
; 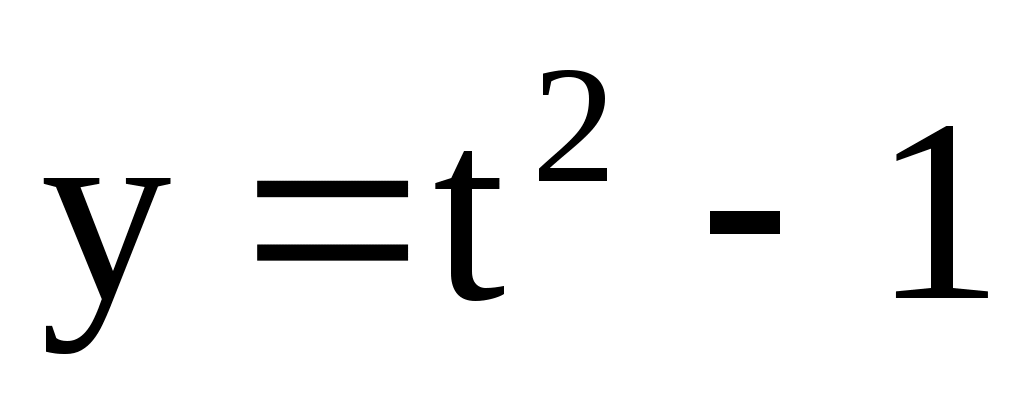 .
.
4.143.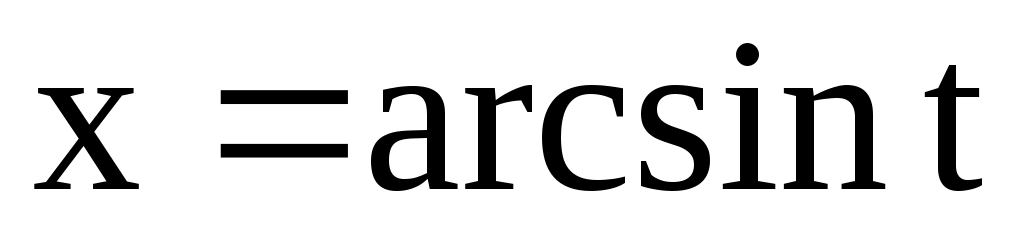 ;
; 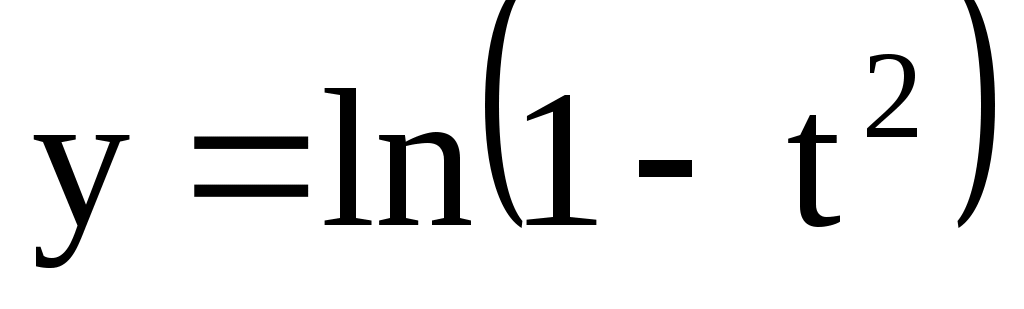 . 4.144.
. 4.144. 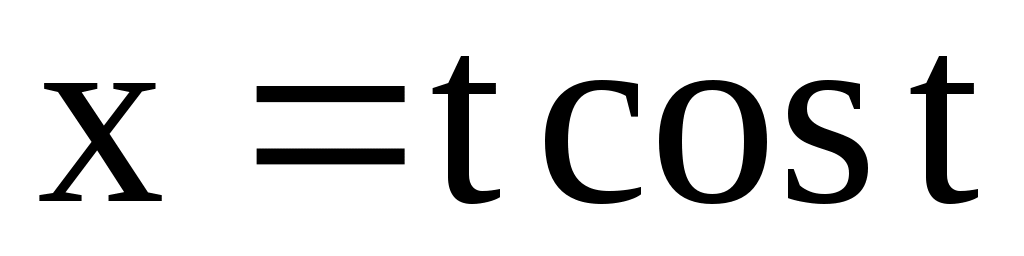 ;
;  .
.
4.145. ;
;  . 4.146.
. 4.146. 
;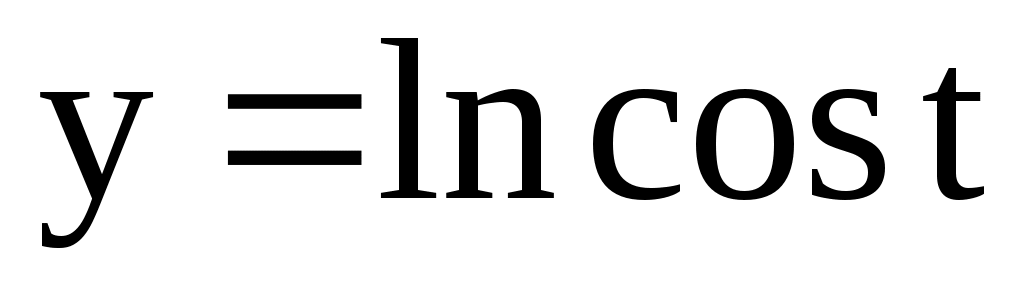 .
.
4.147.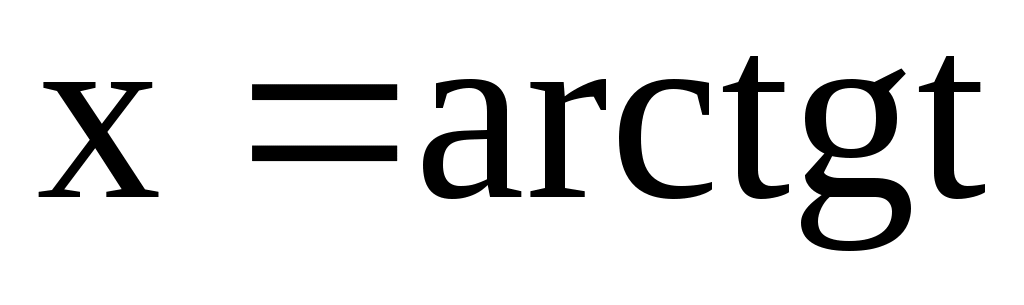 ;
; 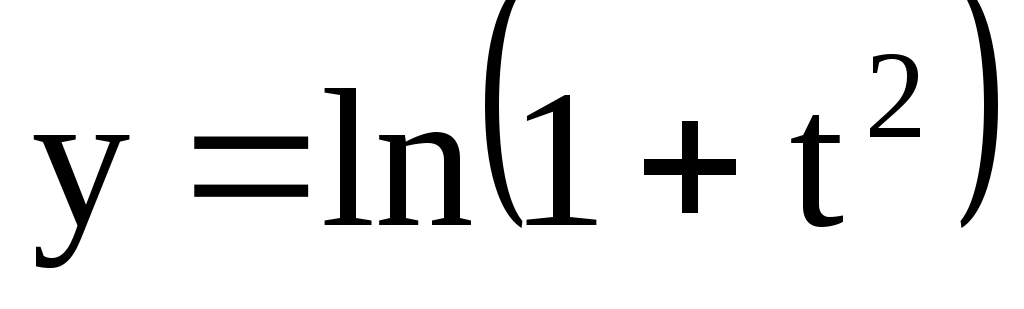 . 4.148.
. 4.148. 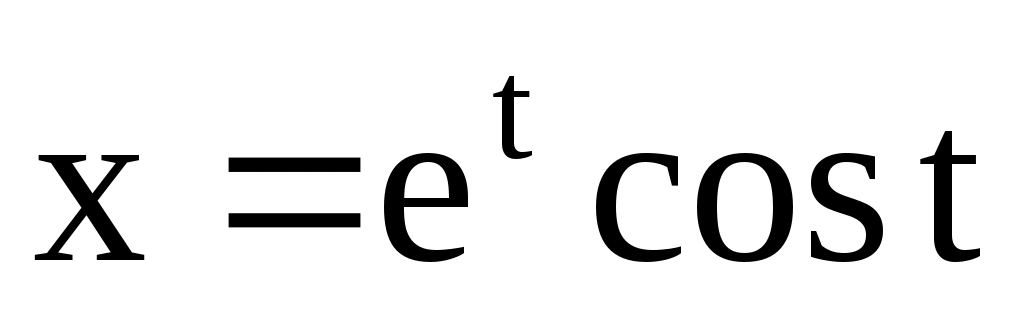 ;
; 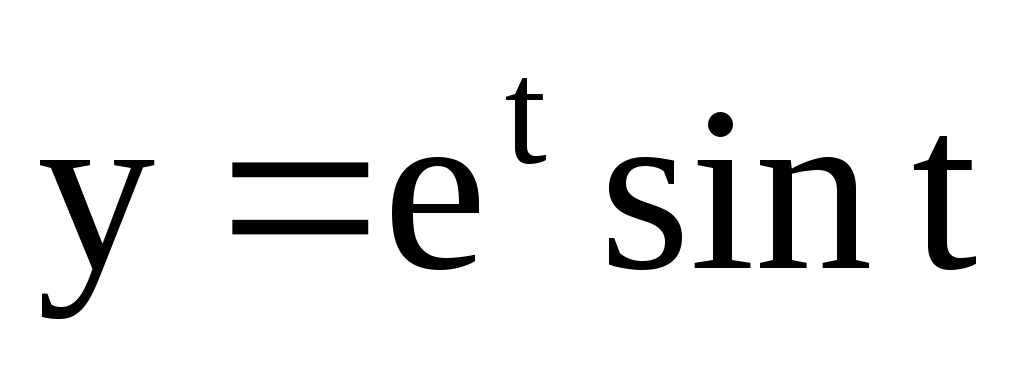 .
.
4.149.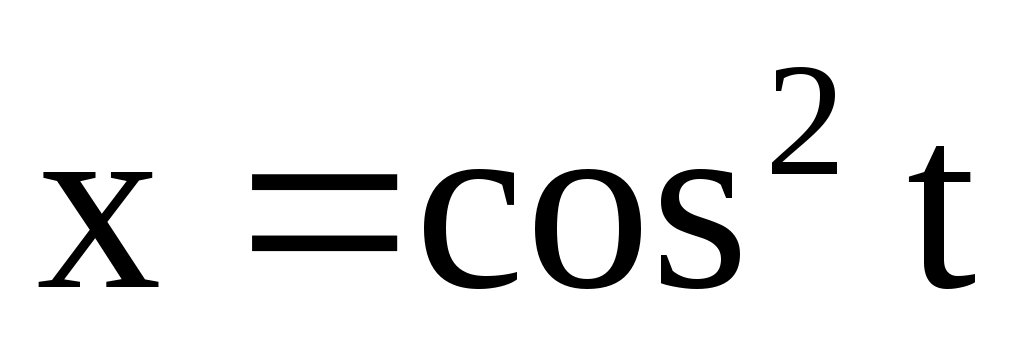 ;
; 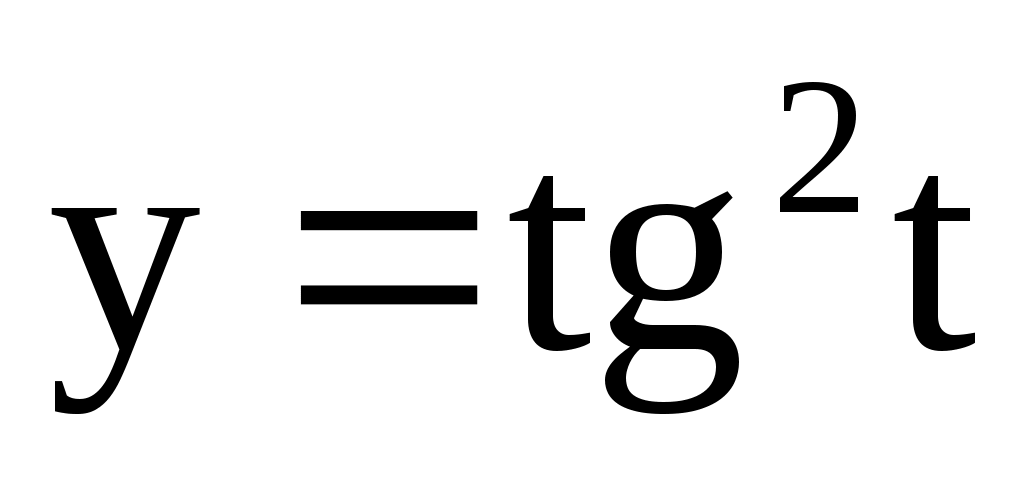 . 4.150.
. 4.150. 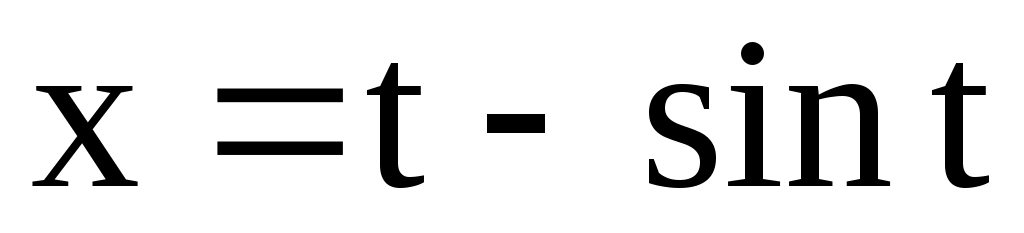 ;
; 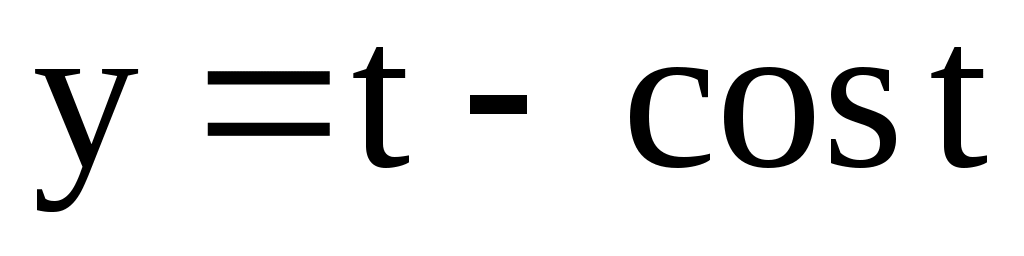 .
.
4.151.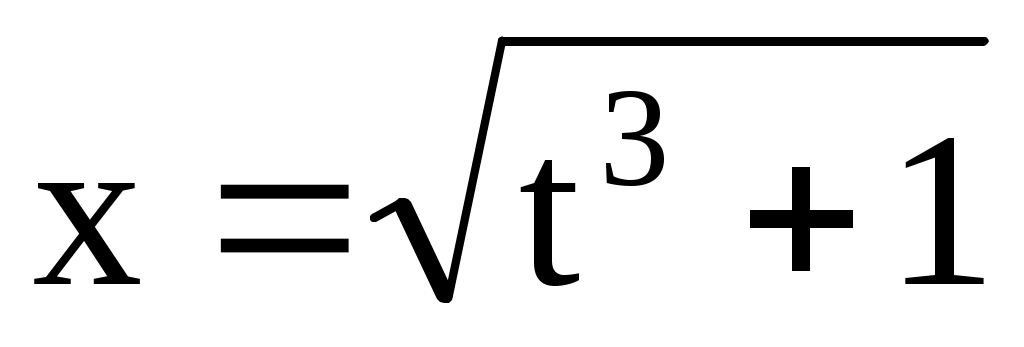 ;
; 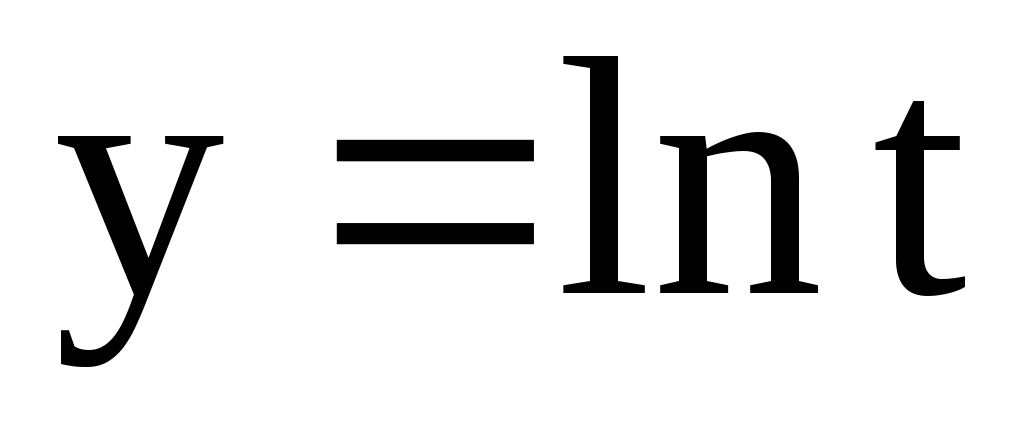 . 4.152.
. 4.152. 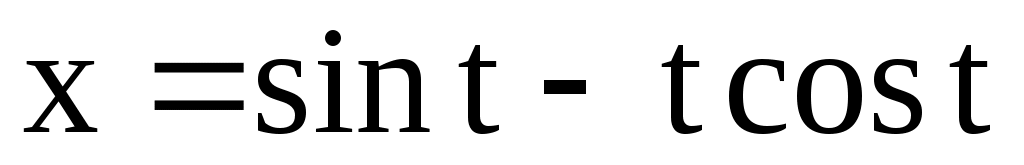 ;
; 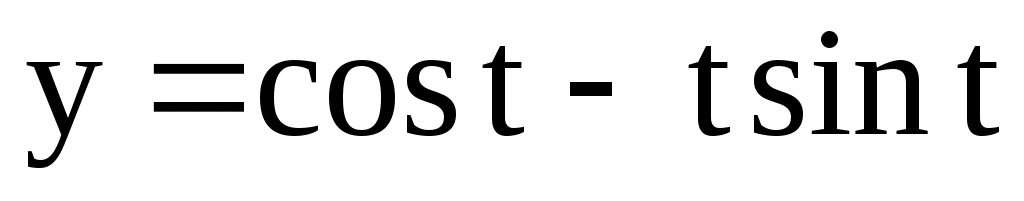 .
.
4.153.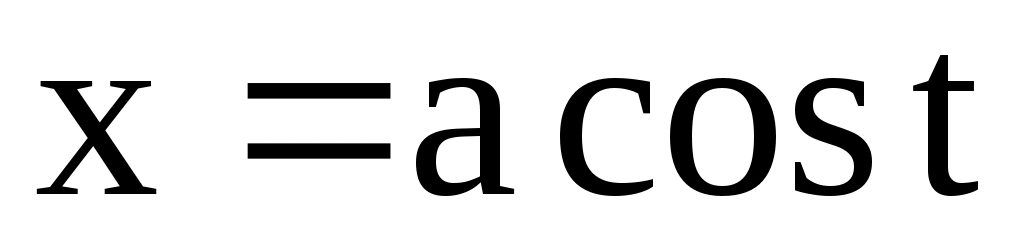 ;
; 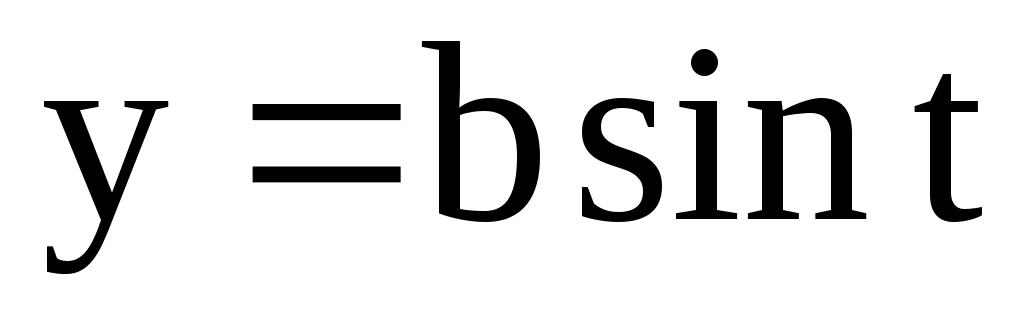 . Найти
. Найти 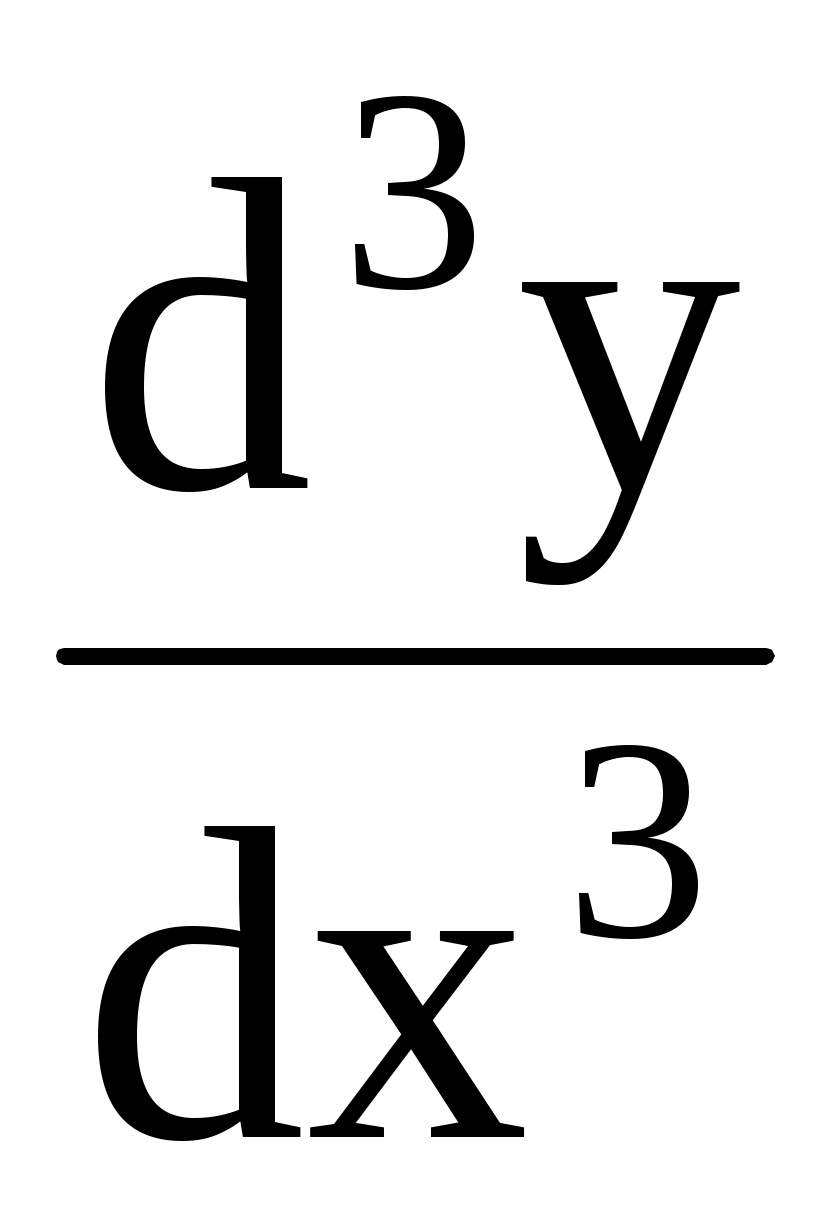 .
.
4.154.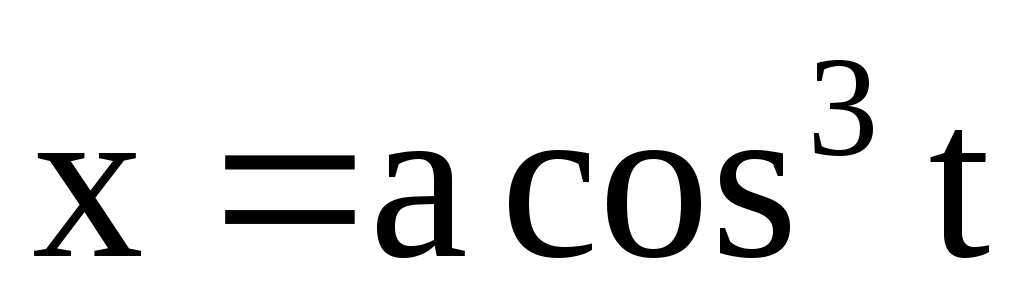 ;
;  . Найти
. Найти 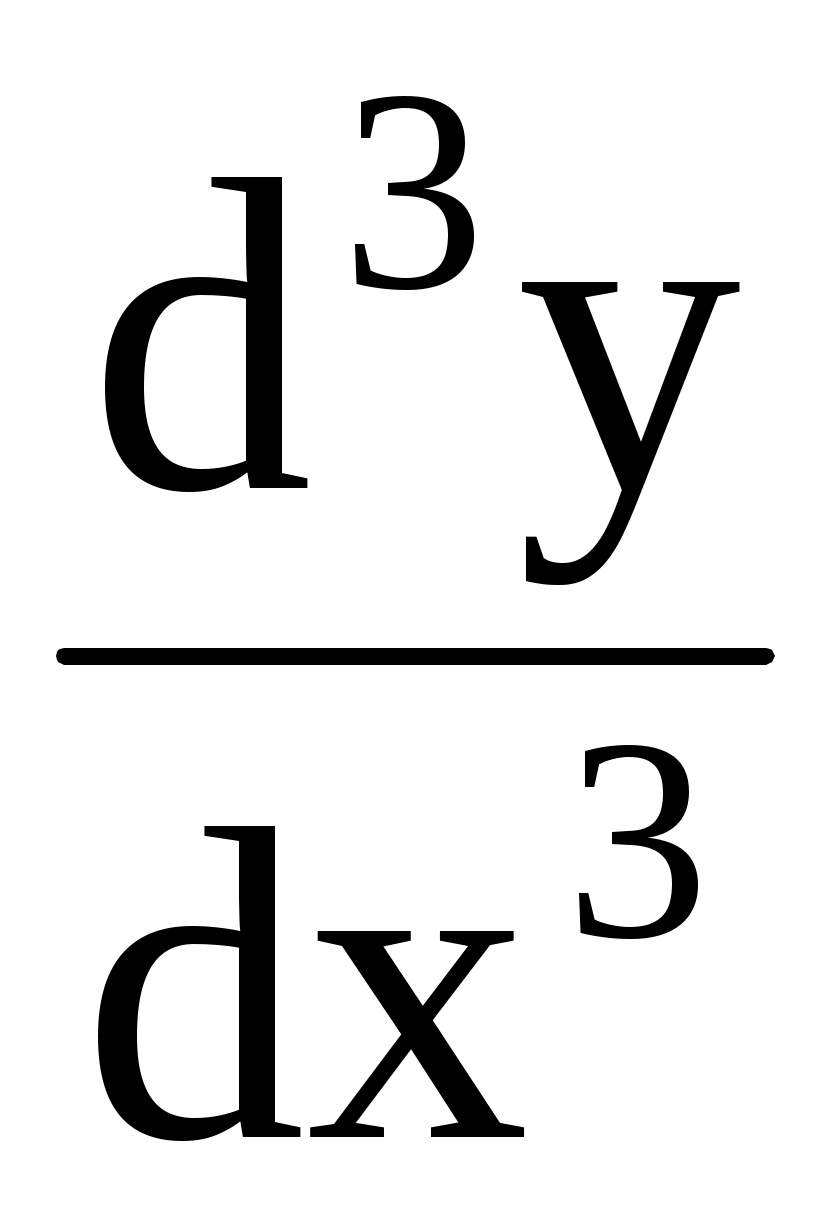 .
.
4.155. Для заданных функций найти дифференциалы 2-го порядка:
1)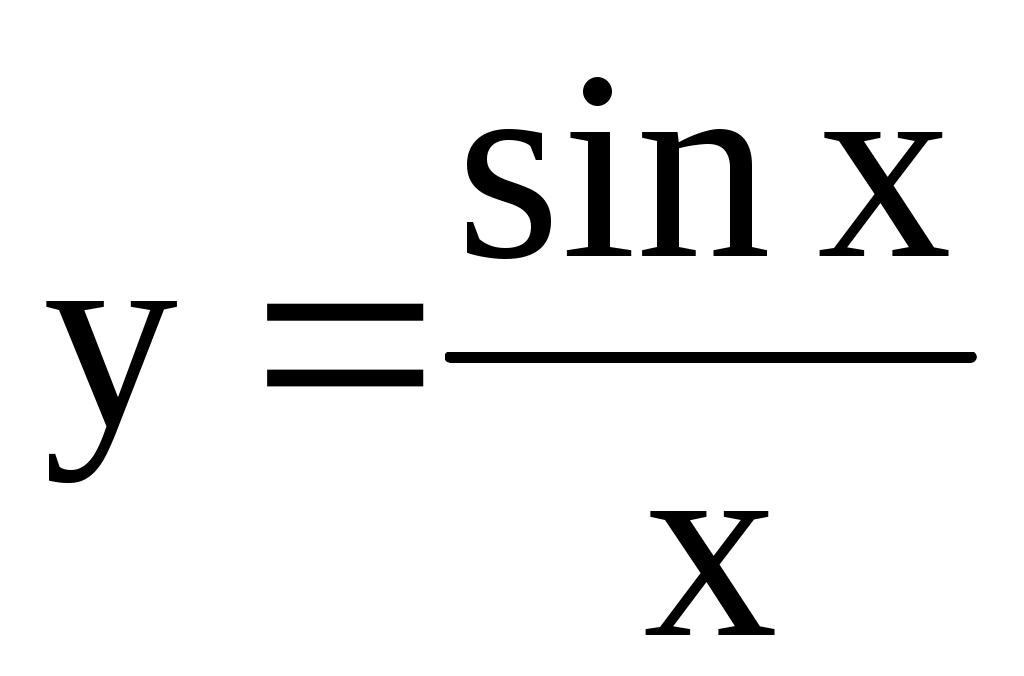 ; 2)
; 2) 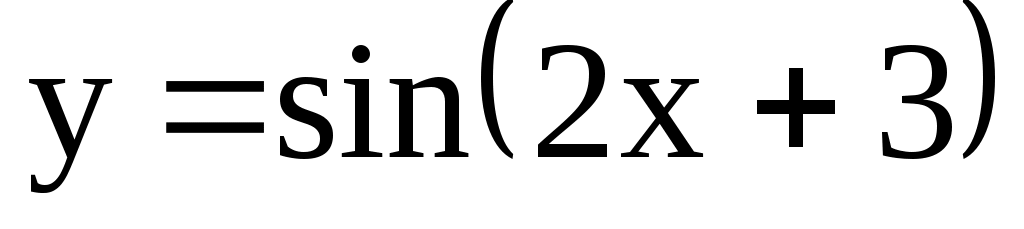 ; 3)
; 3) 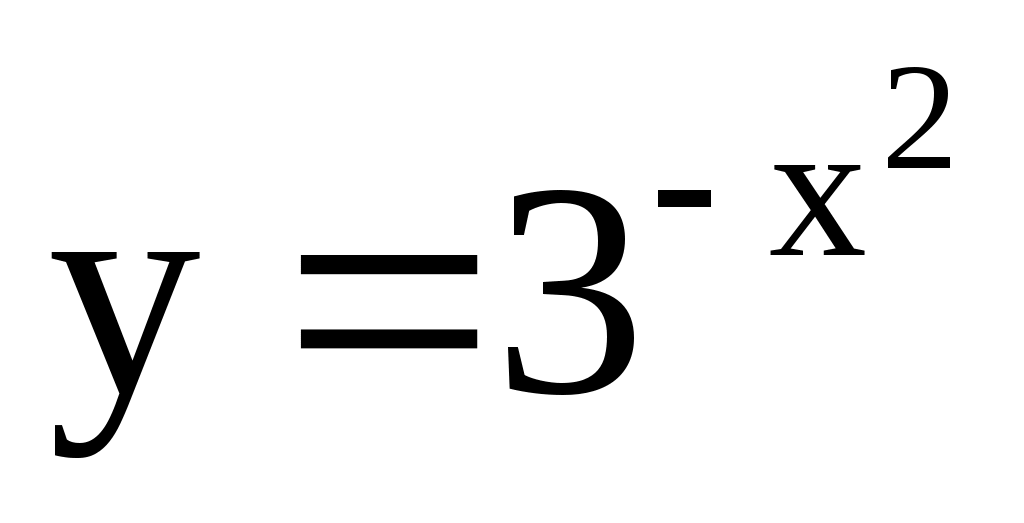 ;
;
4)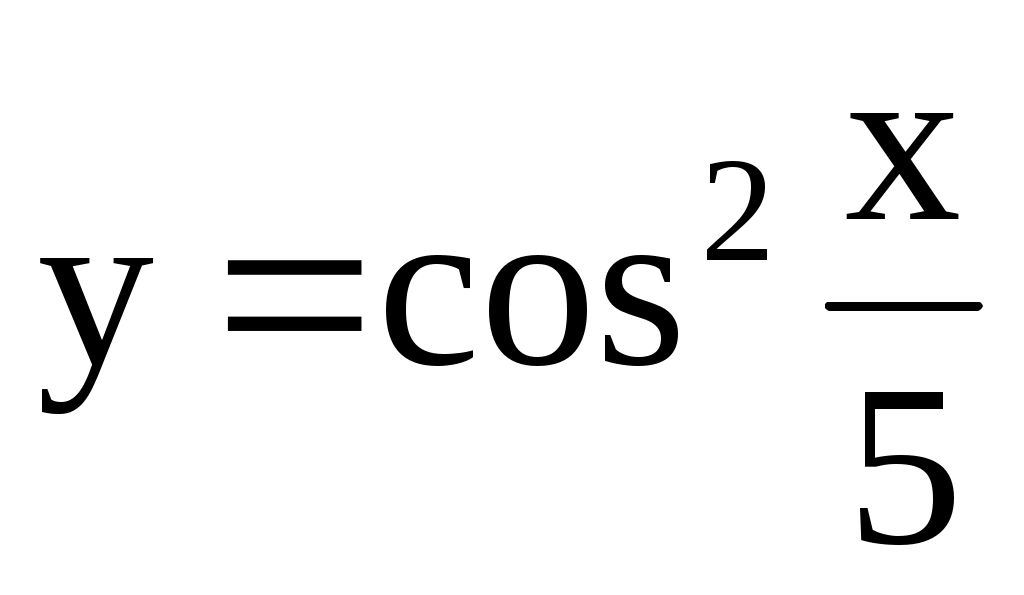 ; 5)
; 5) 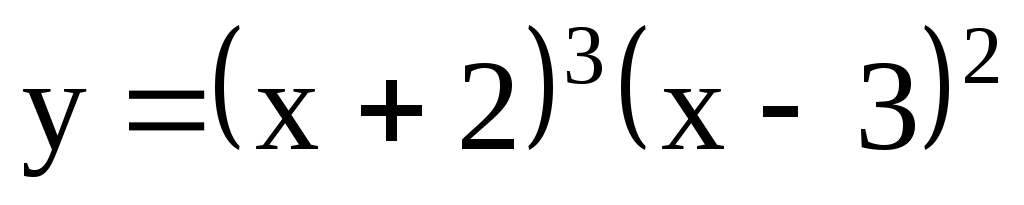 ; 6)
; 6) 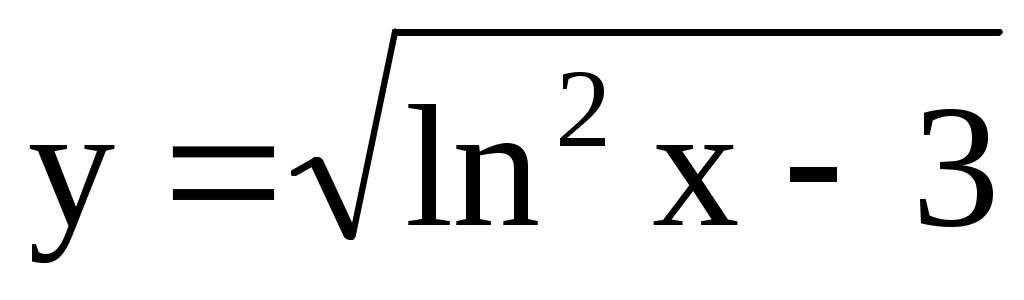 .
.
В задачах 4.156–4.170 найти наибольшее и наименьшее значения заданных функций в указанных промежутках.
4.156.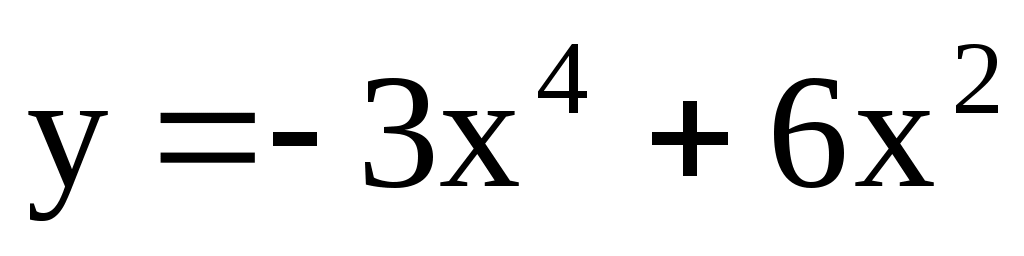
; [–2; 2]. 4.157.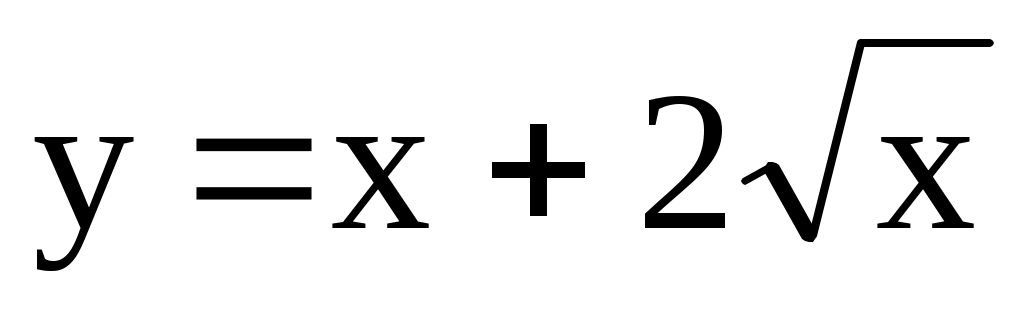 ; [0; 4].
; [0; 4].
4.158.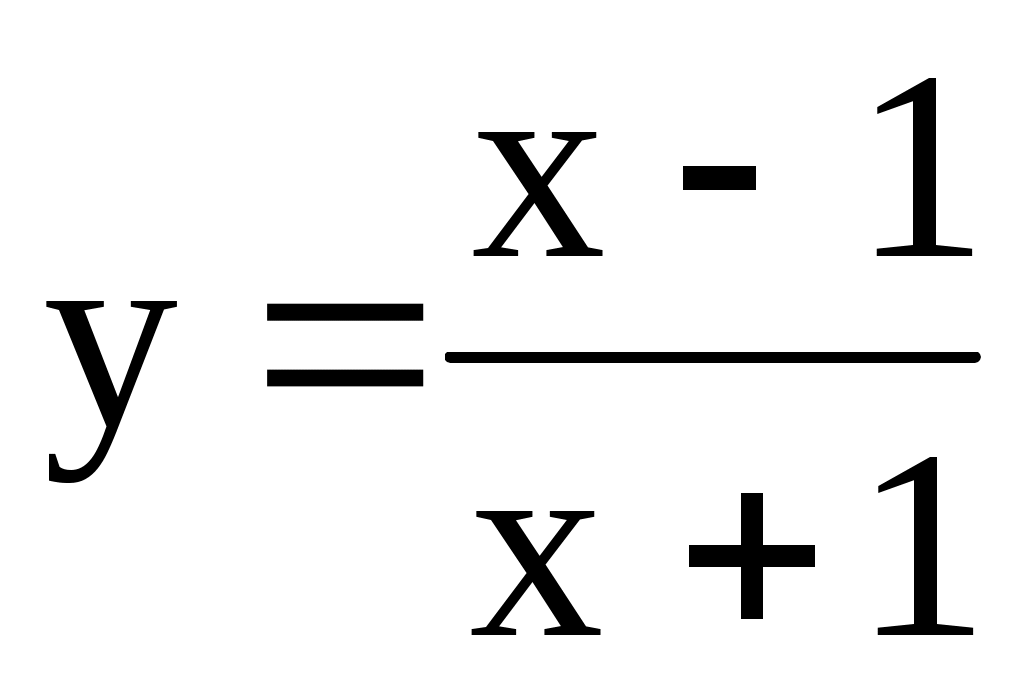 ; [0; 4]. 4.159.
; [0; 4]. 4.159. 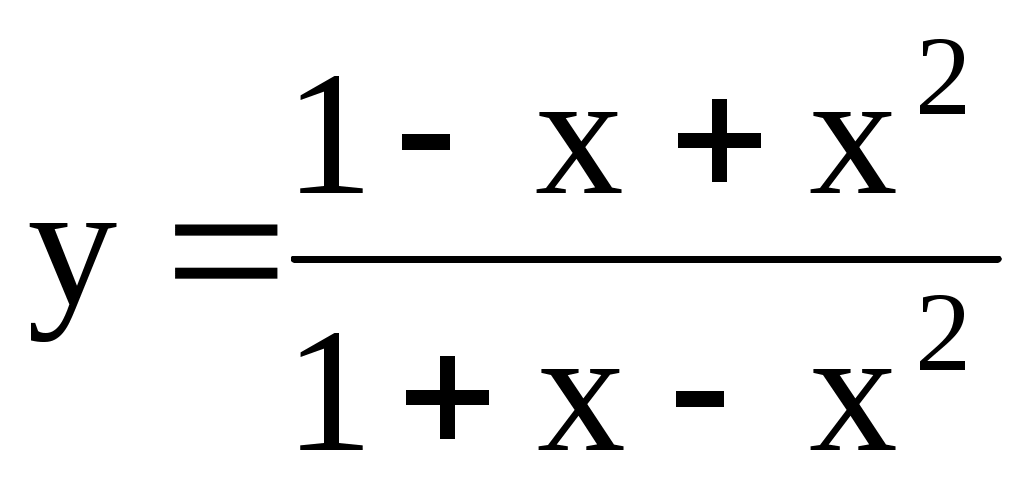 ; [0; 1].
; [0; 1].
4.160.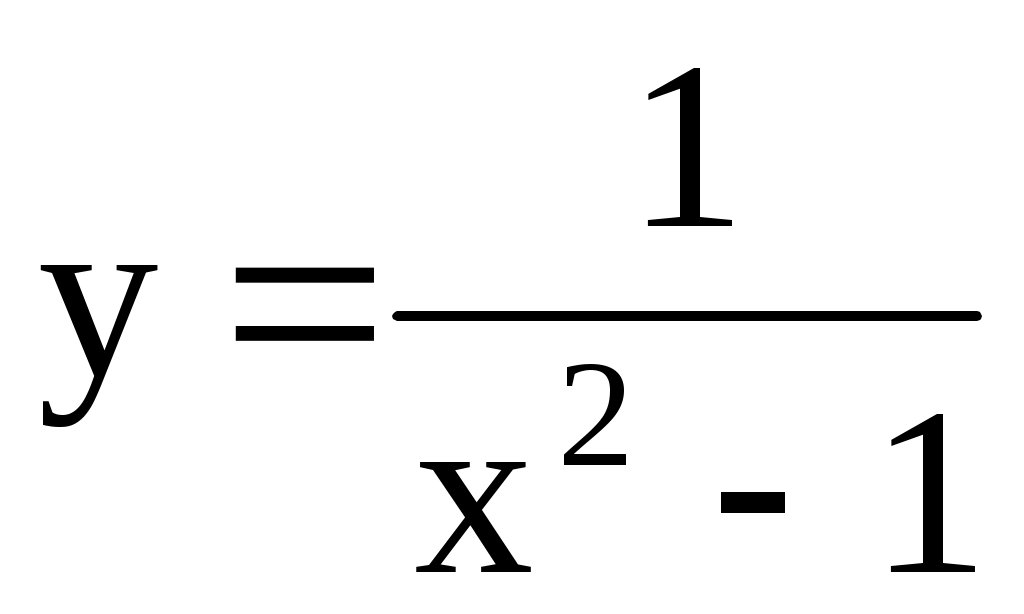 ;
; 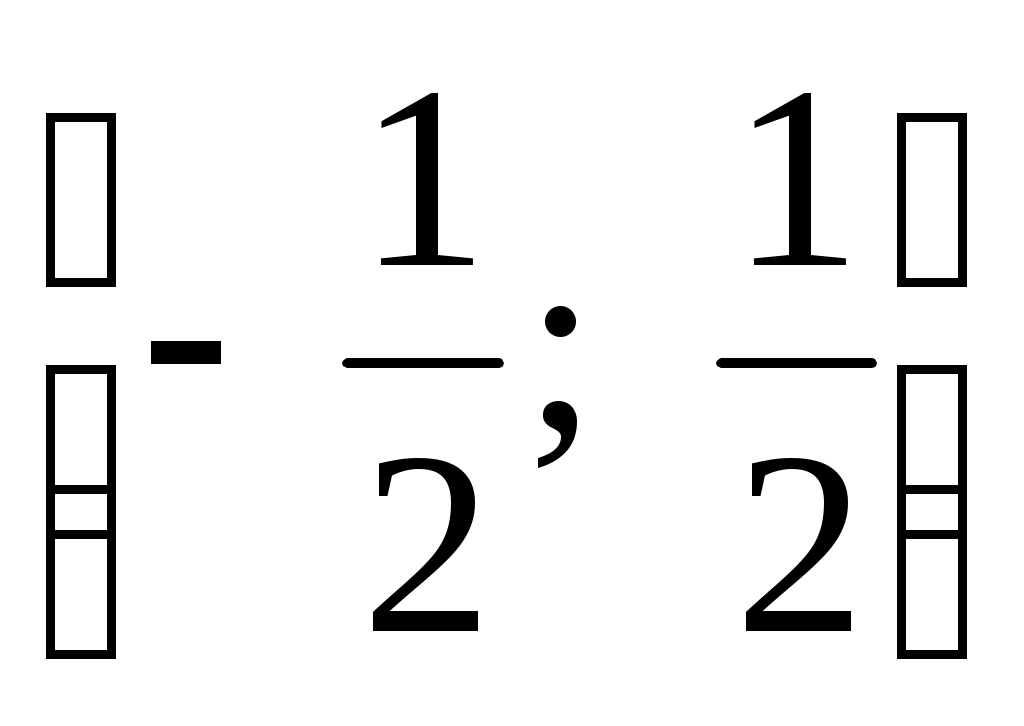 ;. 4.161.
;. 4.161. 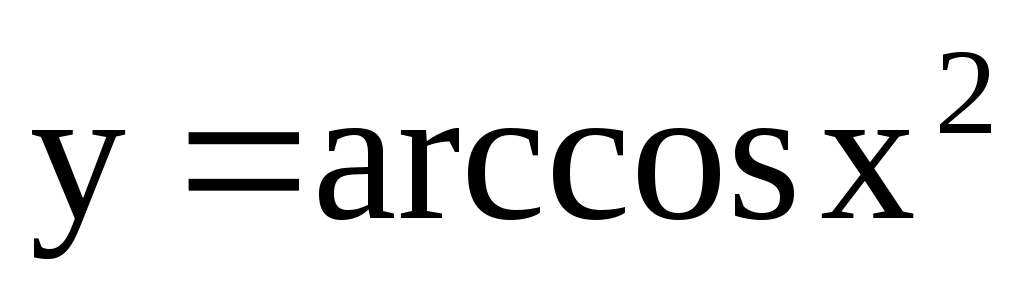 ;
; 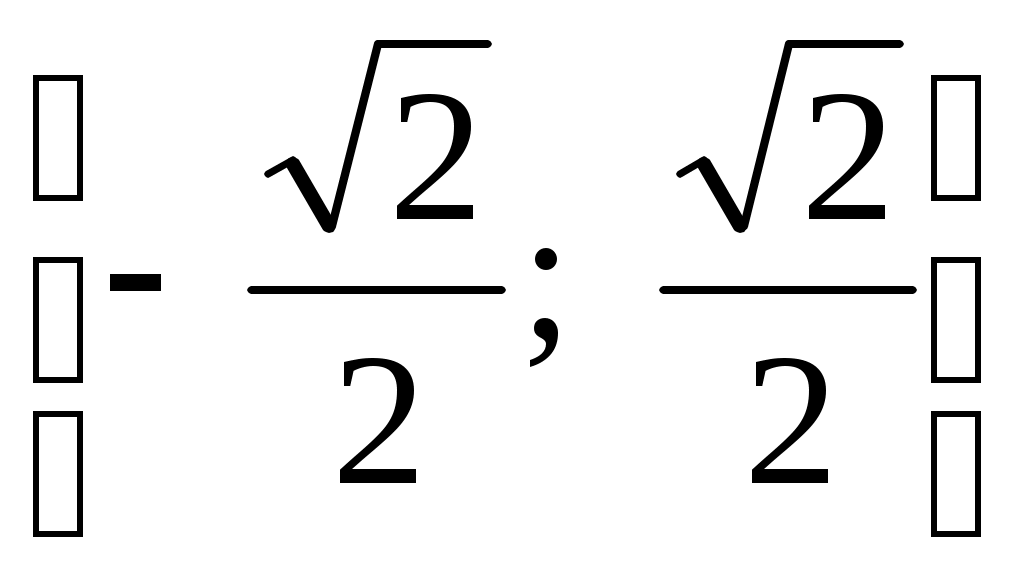 .
.
4.162.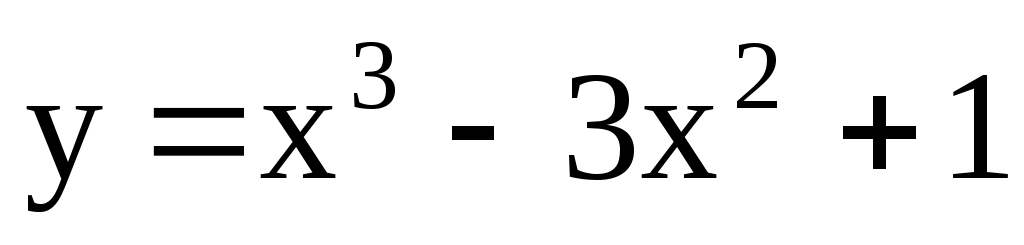 ; [-1; 4]. 4.163.
; [-1; 4]. 4.163. 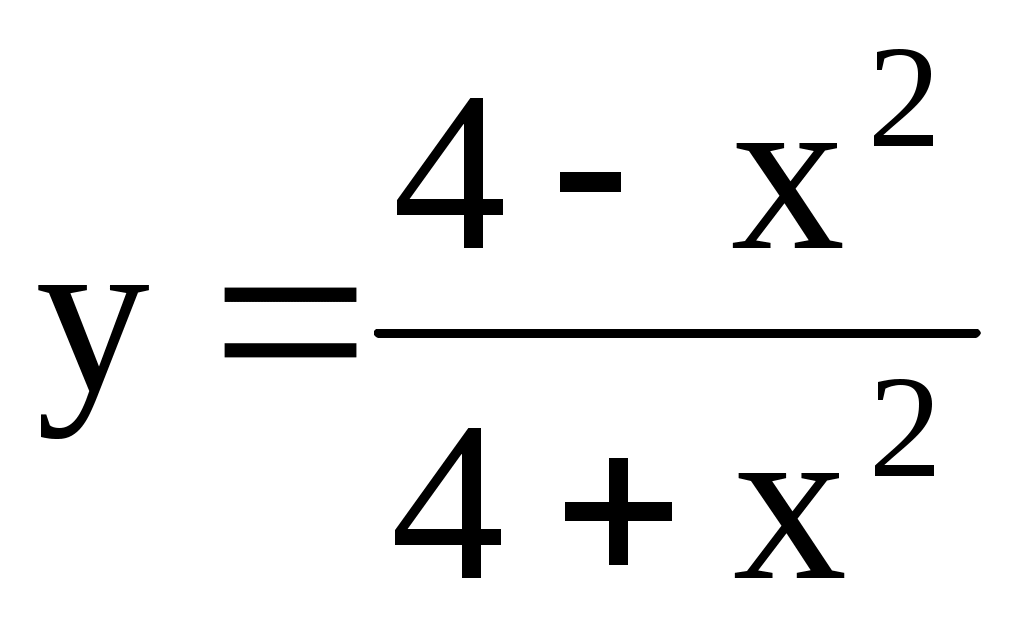 ; [–1; 3].
; [–1; 3].
4.164.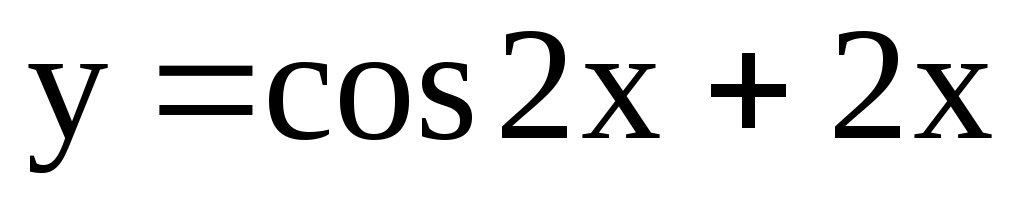 ;
; 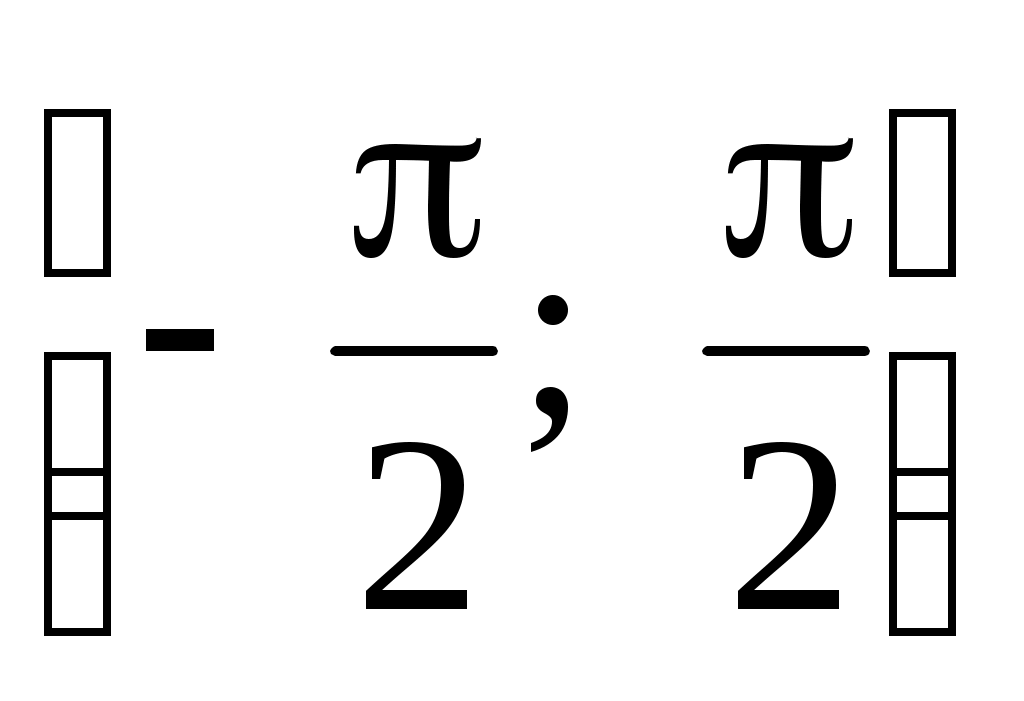 . 4.165.
. 4.165. 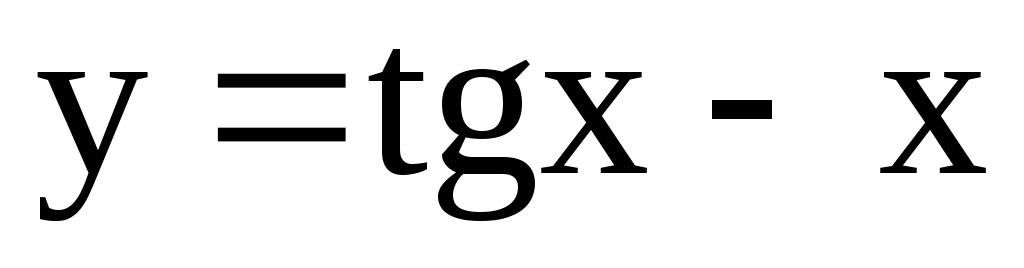 ;
; 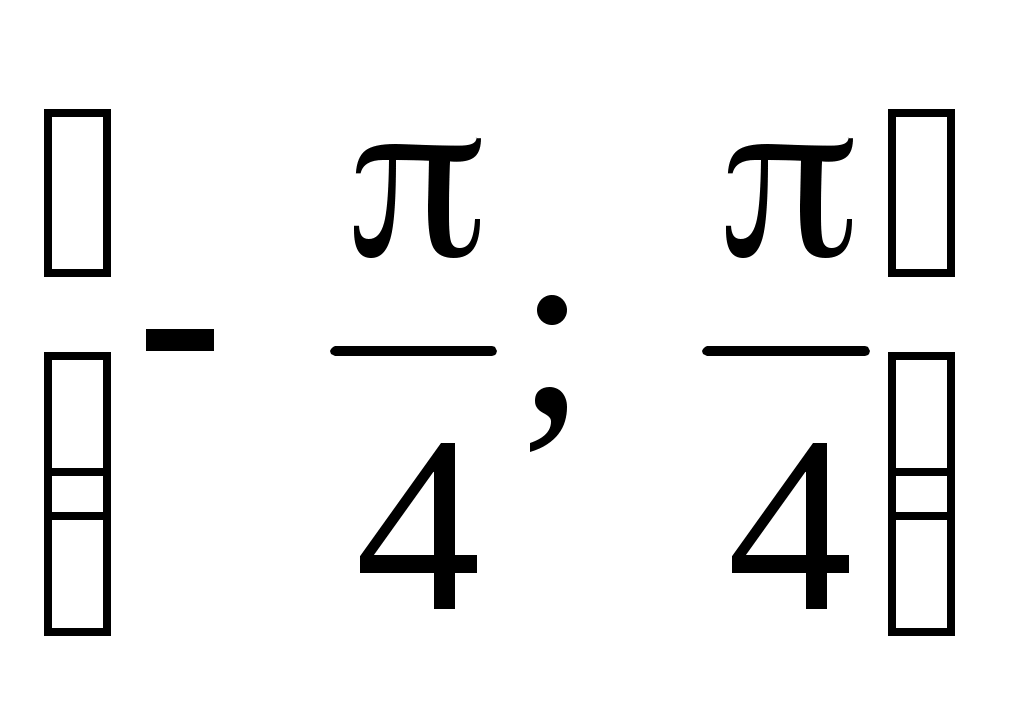 .
.
4.166. ; [–2; 2]. 4.167.
; [–2; 2]. 4.167. 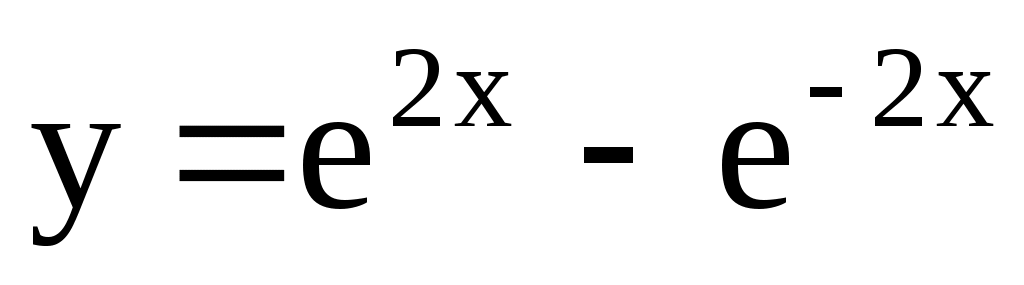 ; [–2; 1].
; [–2; 1].
4.168.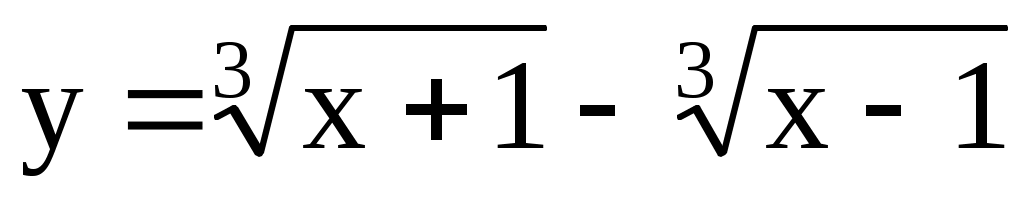 ; [0; 1]. 4.169.
; [0; 1]. 4.169. 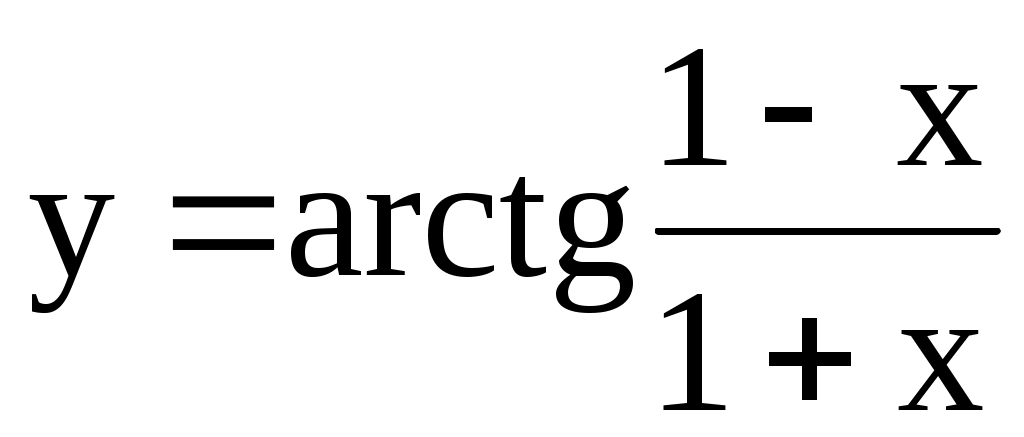 ; [0; 1].
; [0; 1].
4.170.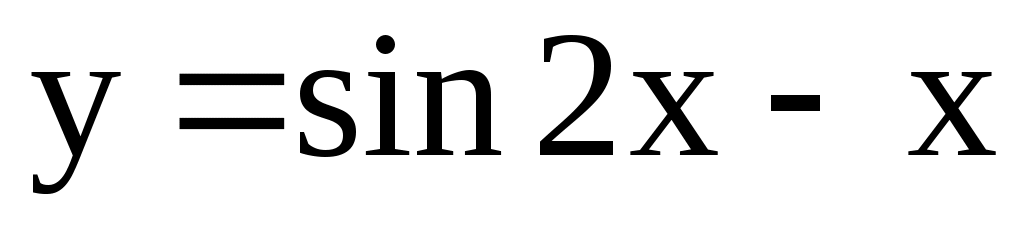 ;
; 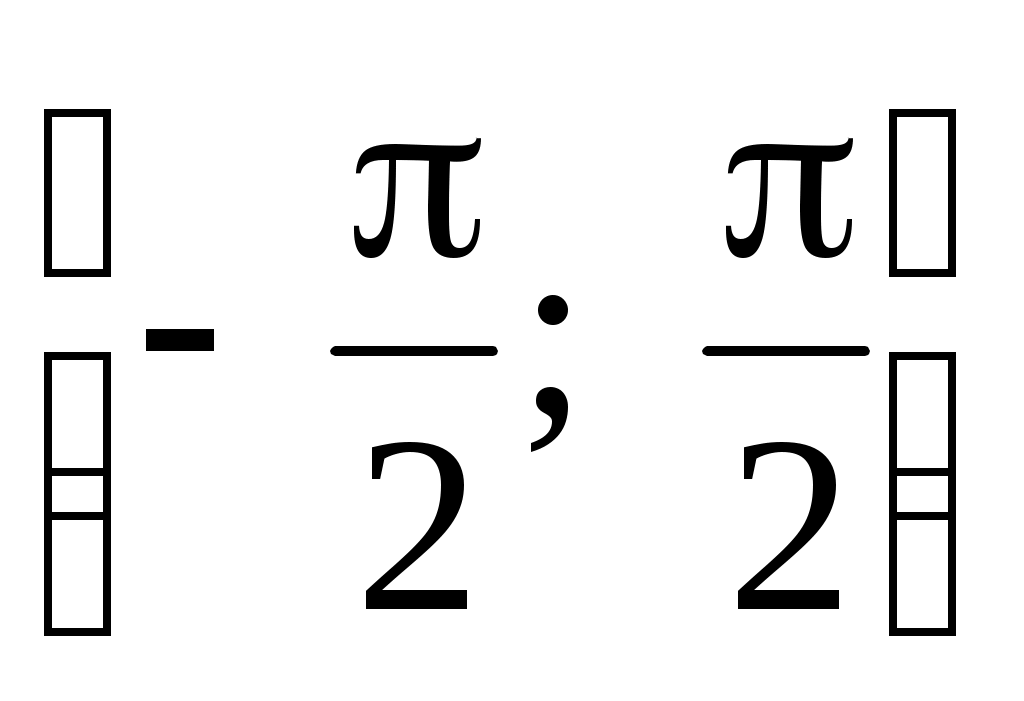 .
.
Задачи на отыскание наибольших и наименьших значений функций
4.171. Число 8 разбить на два таких слагаемых, чтобы сумма их кубов была наименьшей.
4.172. Число 36 разложить на два таких множителя, чтобы сумма их квадратов была наименьшей.
4.173. Из углов квадратного листа картона размером 1818 см2, нужно вырезать одинаковые квадраты так, чтобы согнув лист, получить коробку наибольшей вместимости. Какова должна быть сторона вырезаемого квадрата?
4.174. Открытый чан имеет форму цилиндра. При данном объёме V каковы должны быть радиус основания и высота цилиндра
, чтобы его поверхность была наименьшей.
4.175. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы её объём был наибольшим.
4.176. Найти высоту цилиндра наибольшего объёма, который можно вписать в шар радиуса R.
4.177. Найти высоту конуса наибольшего объёма, который можно вписать в шар радиуса R.
4.178. Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
4.179. Бревно длиной в 20 м имеет форму усечённого конуса, диаметры оснований которого равны соответственно 2 и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна и объём которой был бы наибольшим. Каковы должны быть размеры балки?
4.180. Катер стоит на якоре в 9 км от ближайшей точки берега; с катера нужно послать гонца в лагерь, расположенный в 15 км, считая по берегу от ближайшей к катеру точки берега (лагерь расположен на берегу). Если гонец может делать пешком по 5 км/ч, а на вёслах по 4 км/ч, то в каком пункте берега он должен пристать, чтобы попасть в лагерь в кратчайшее время?
4.181. Картина в 1,4 м высотой повешена на стену так, что её нижний край на 1,8 м выше глаза наблюдателя. На каком расстоянии от стены должен стать наблюдатель, чтобы его положение было наиболее благоприятным для осмотра картины (т.е. чтобы угол зрения был наибольшим)?
4.182. На странице книги печатный текст должен занимать S квадратных сантиметров. Верхние и нижние поля должны быть по а см, правое и левое по b см. Если принимать во внимание только экономию бумаги, то какими должны быть наиболее выгодные размеры страницы?
В задачах 4.183–4.232 вычислить пределы, пользуясь правилом Лопиталя.
4.183.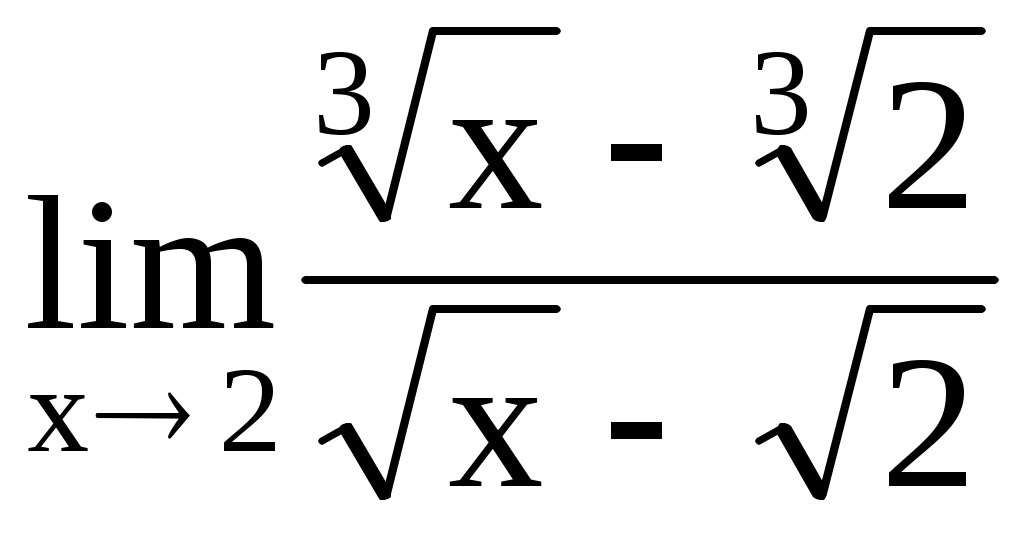 . 4.184.
. 4.184. 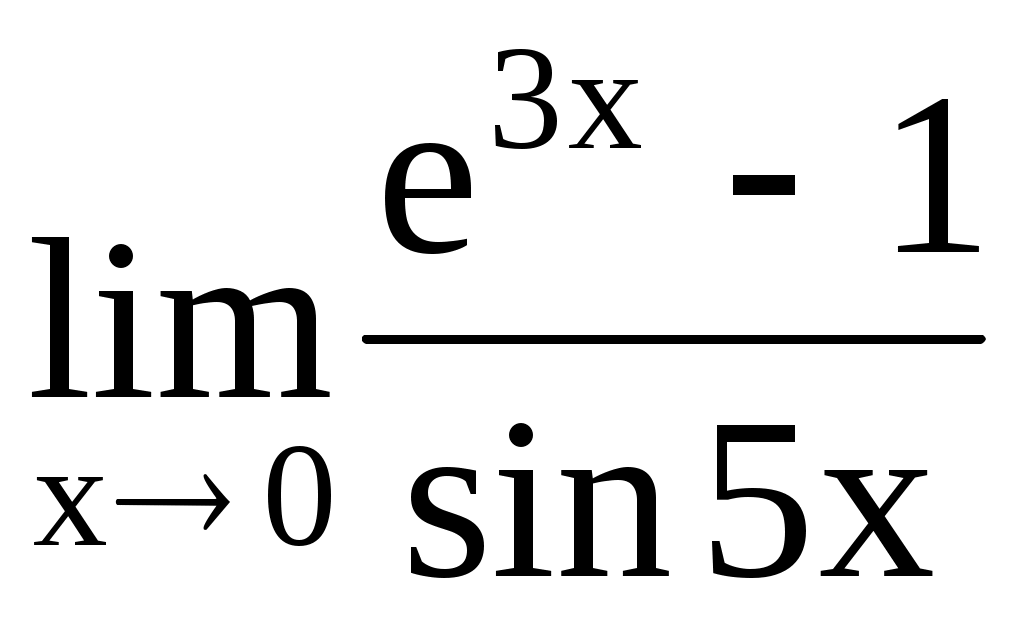 .
.
4.185.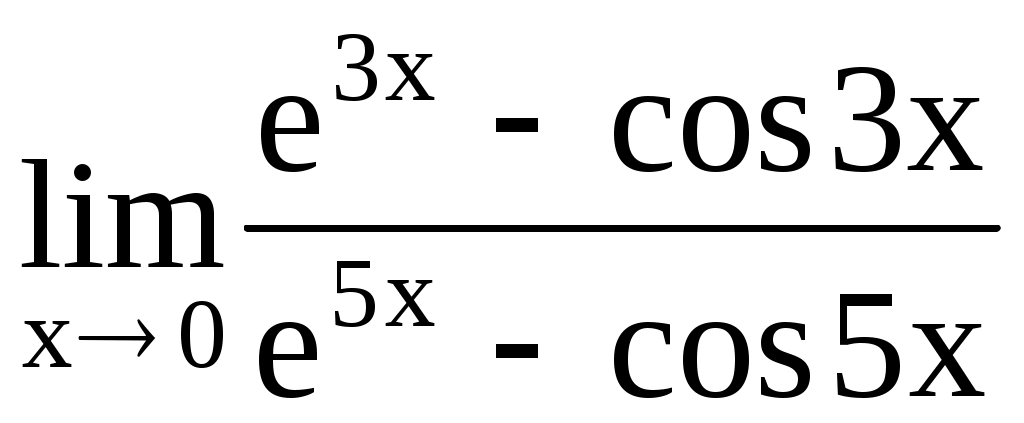 . 4.186.
. 4.186. 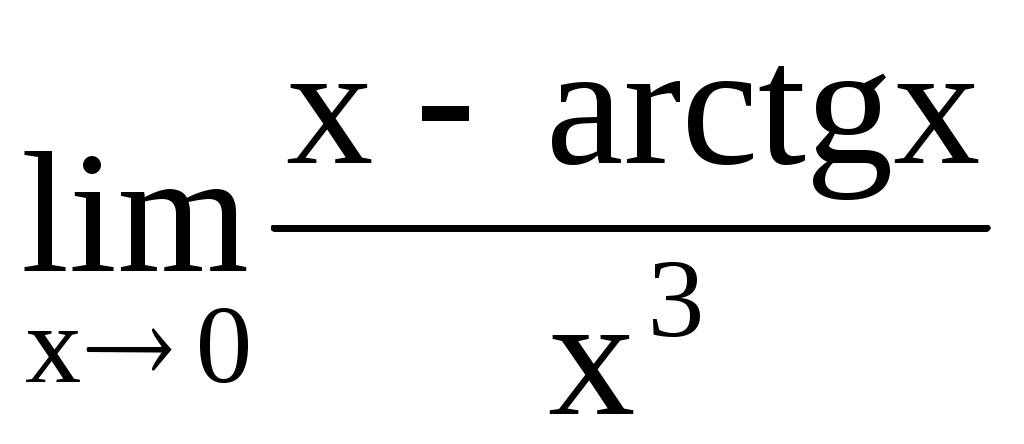 .
.
4.187.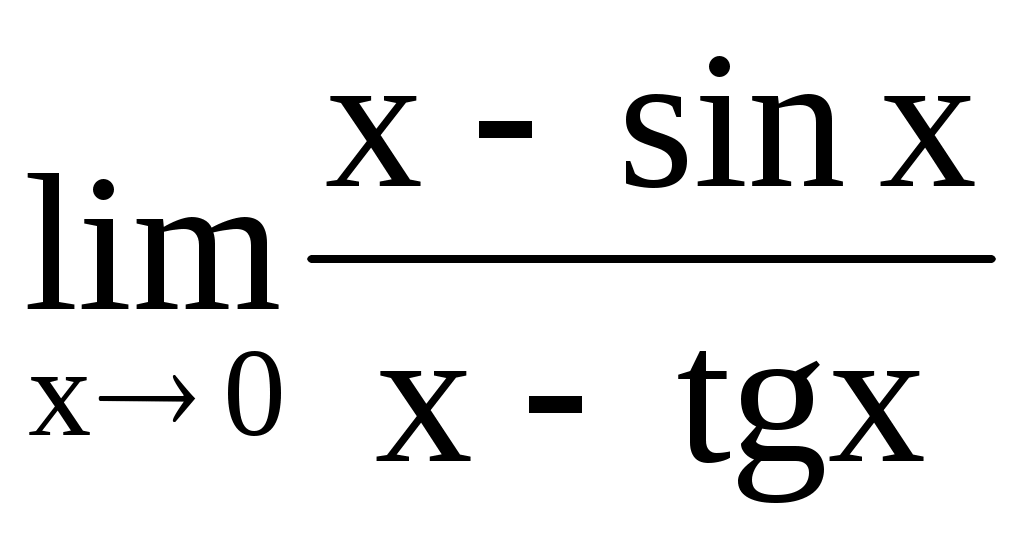 . 4.188.
. 4.188. 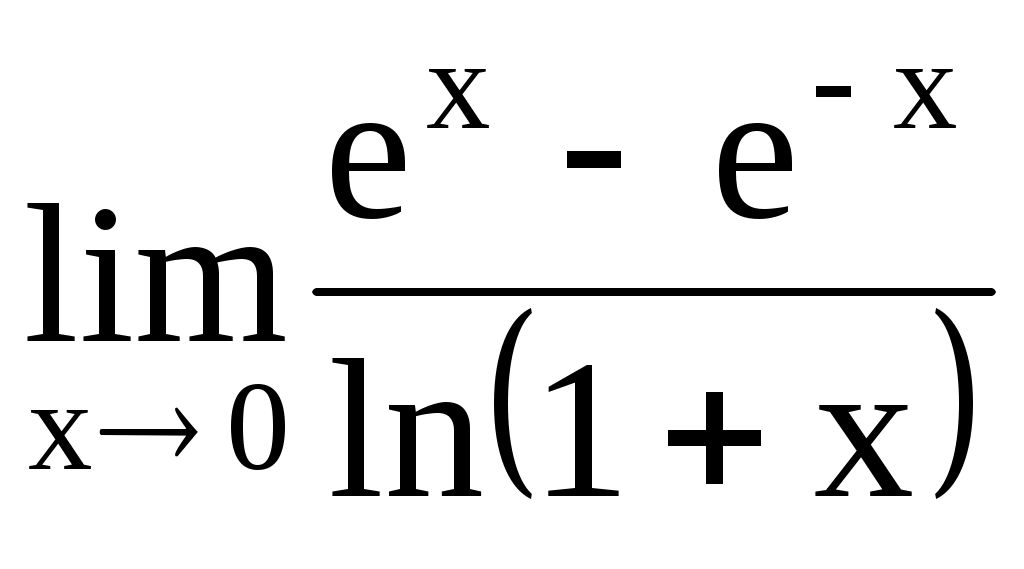 .
.
4.189.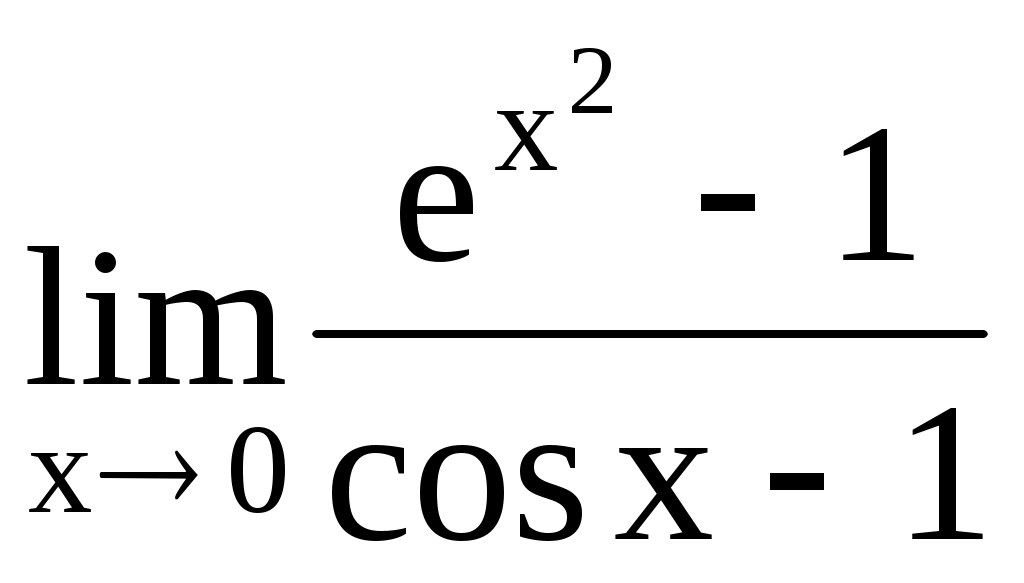 . 4.190.
. 4.190. 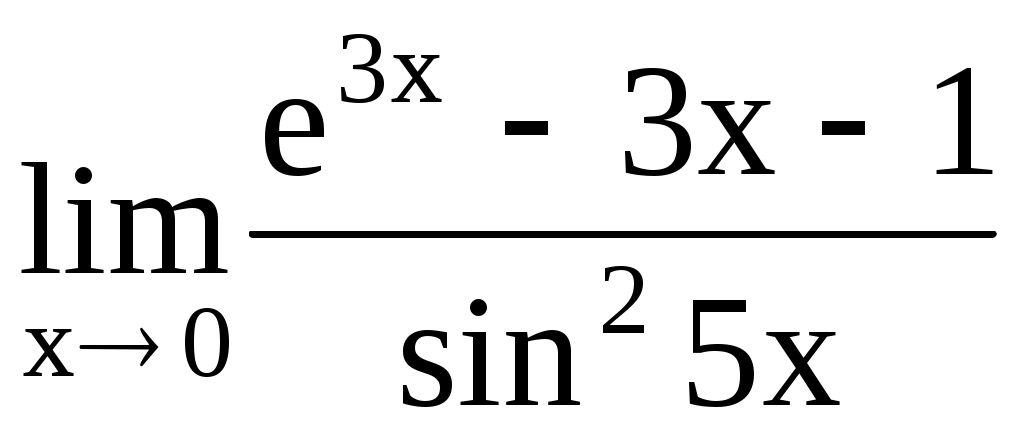
.
4.191.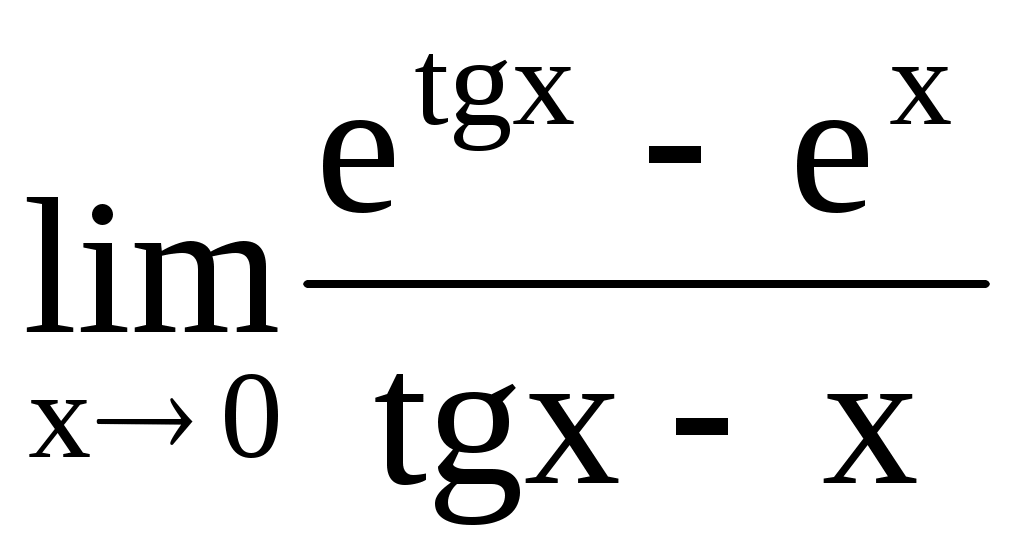 . 4.192.
. 4.192. 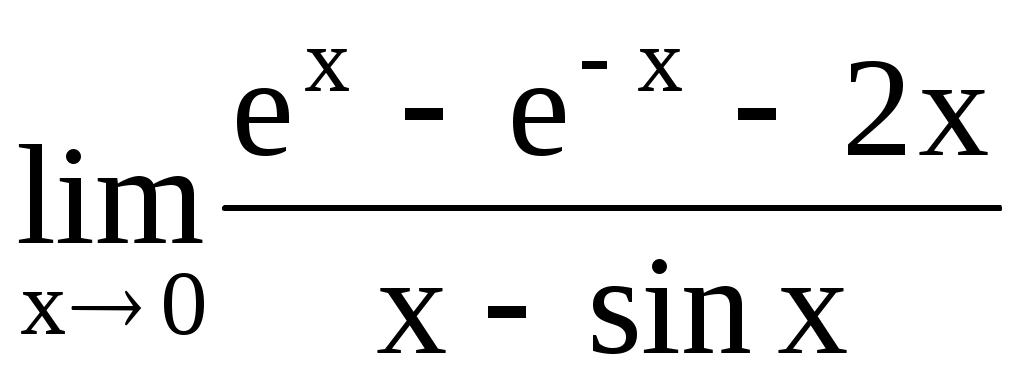 .
.
4.193.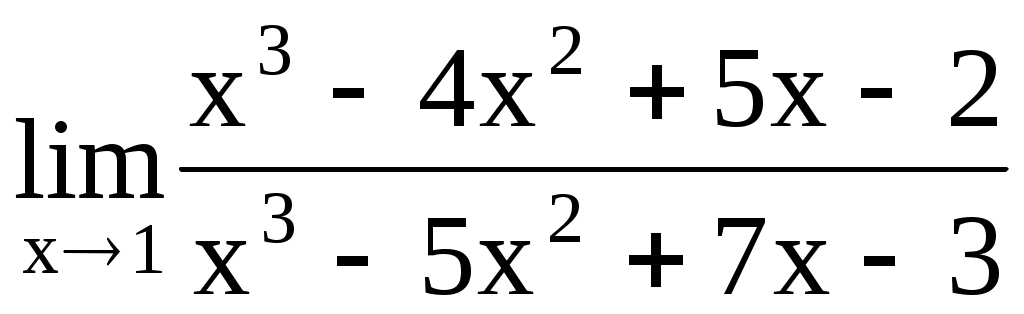 . 4.194.
. 4.194. 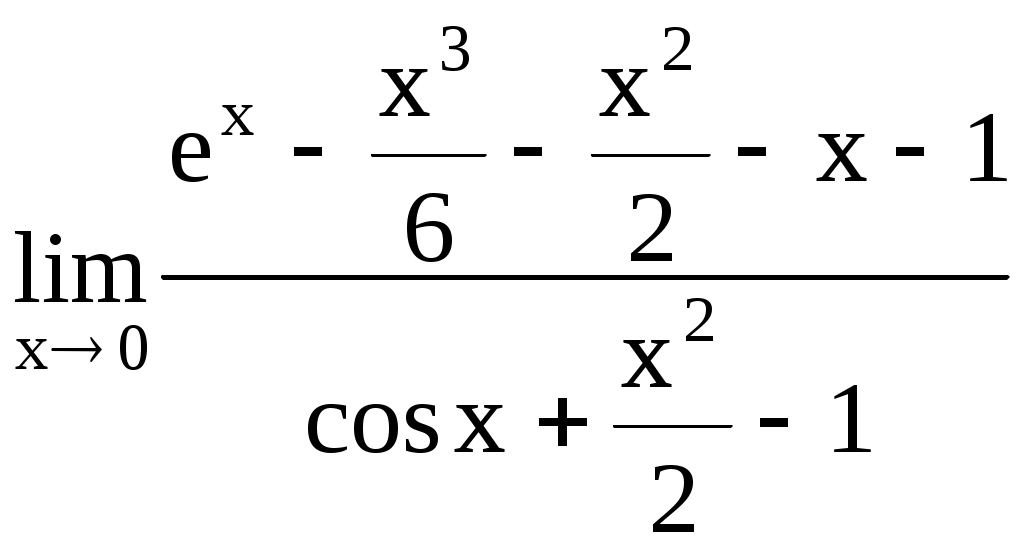 .
.
4.195.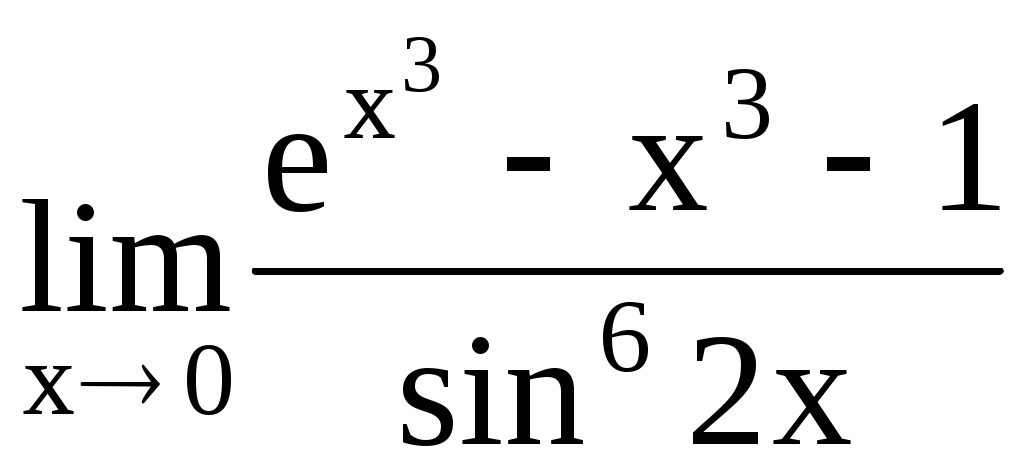 . 4.196.
. 4.196. 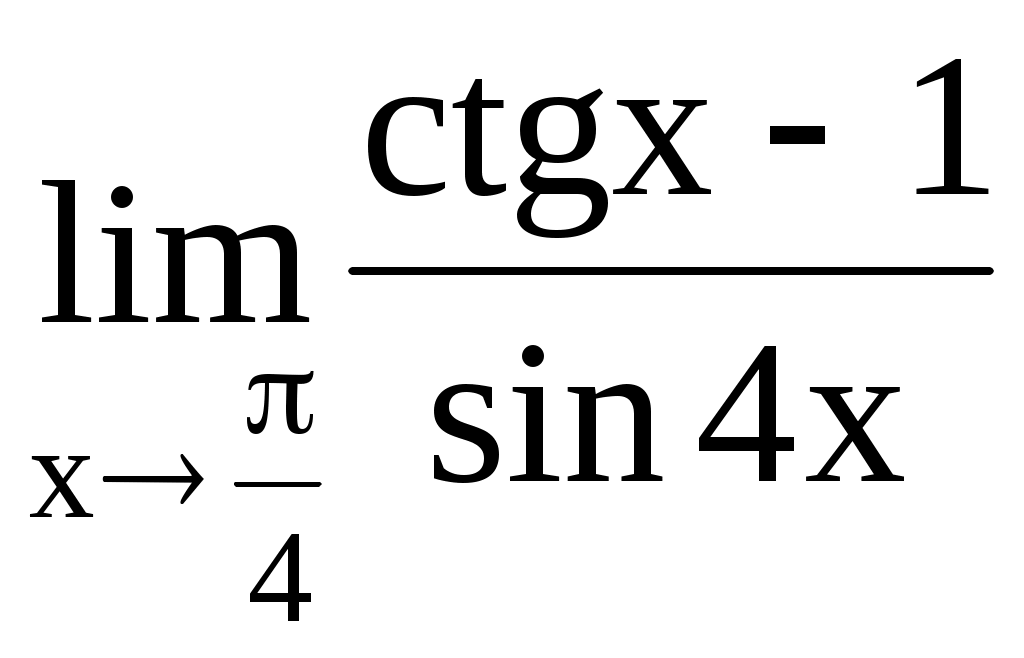 .
.
4.197.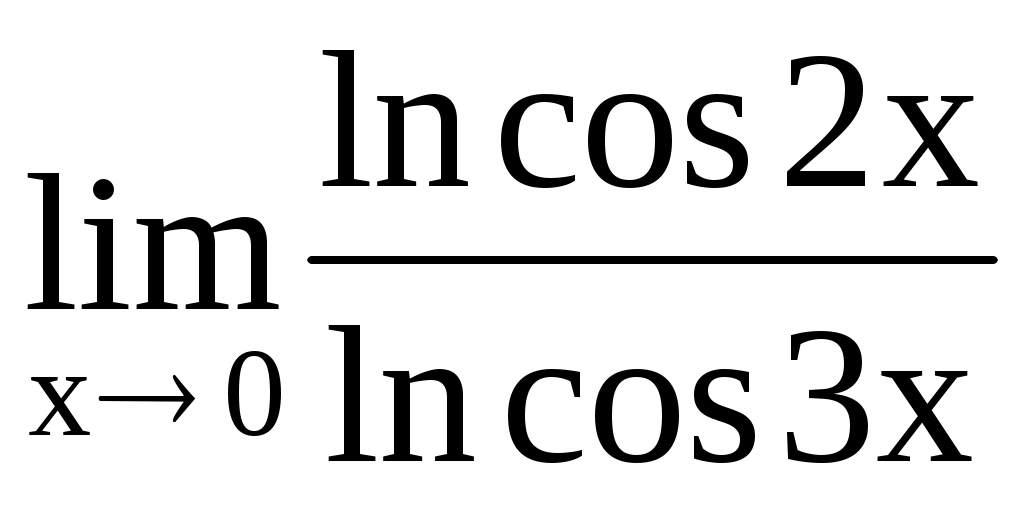 . 4.198.
. 4.198. 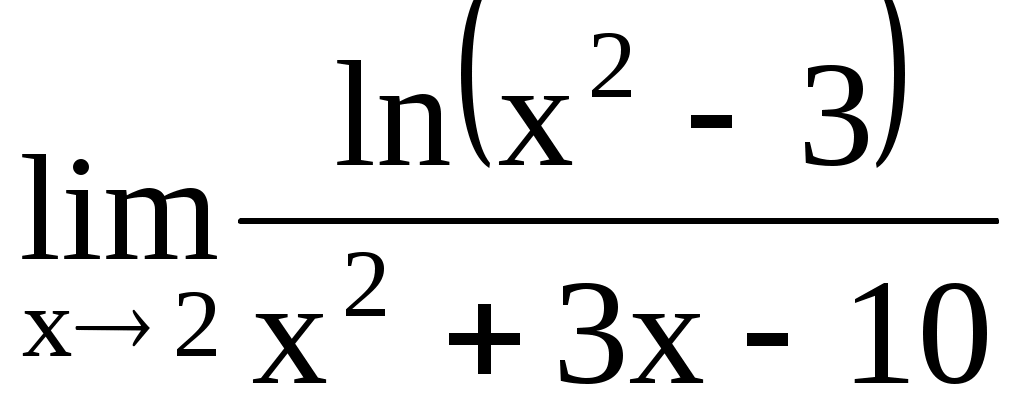 .
.
4.199.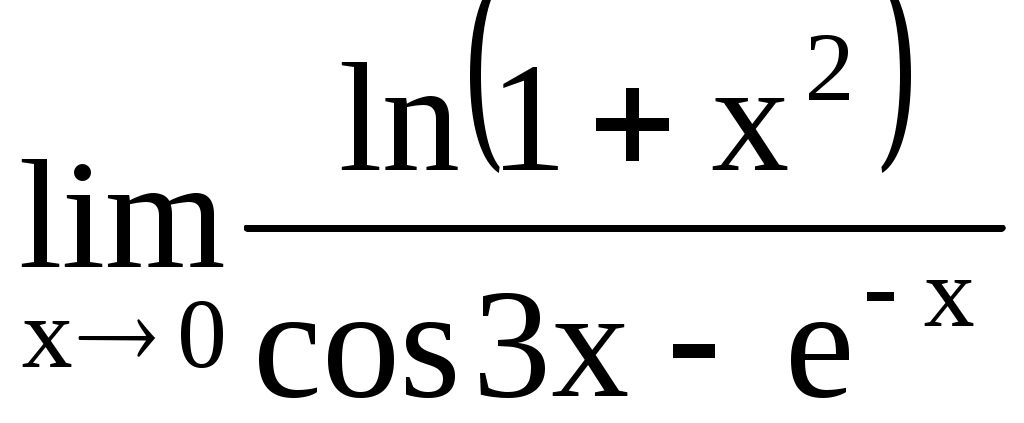 . 4.200.
. 4.200. 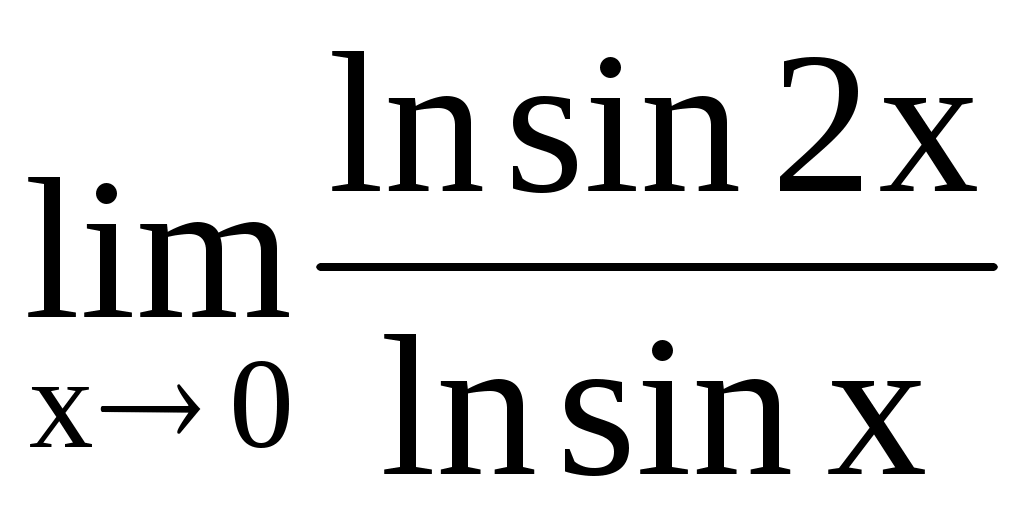 .
.
4.201.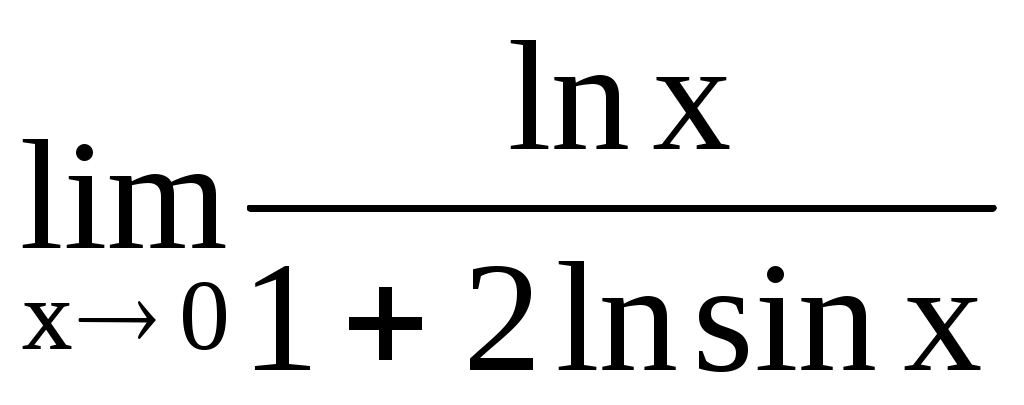 . 4.202.
. 4.202. 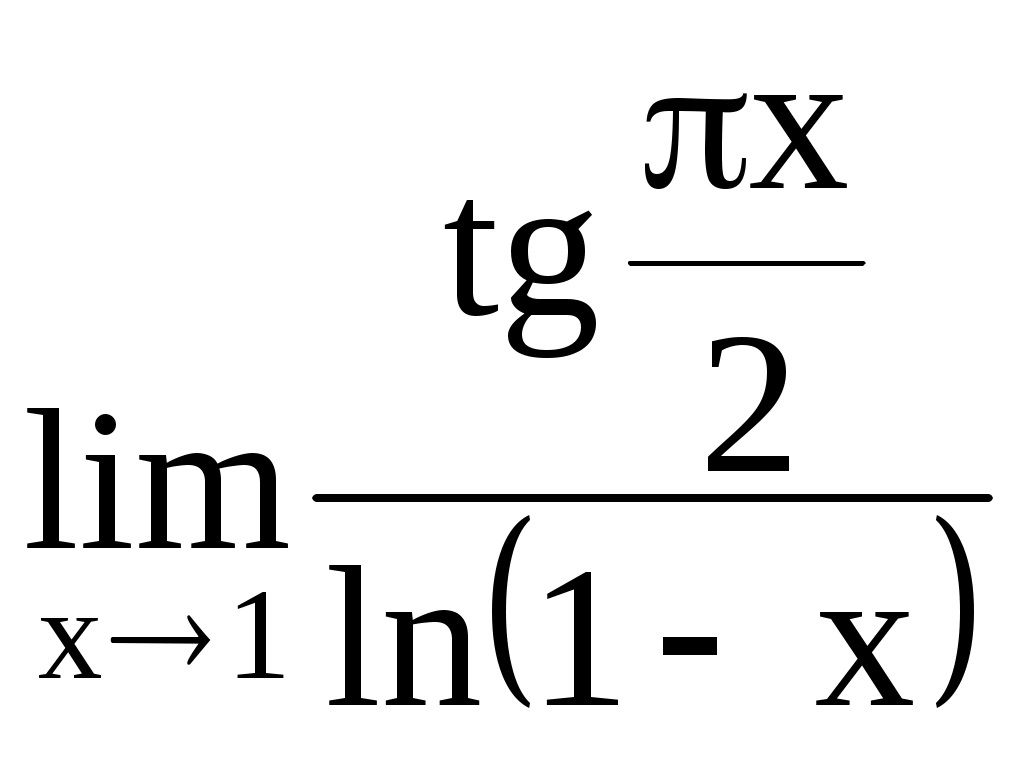 .
.
4.203.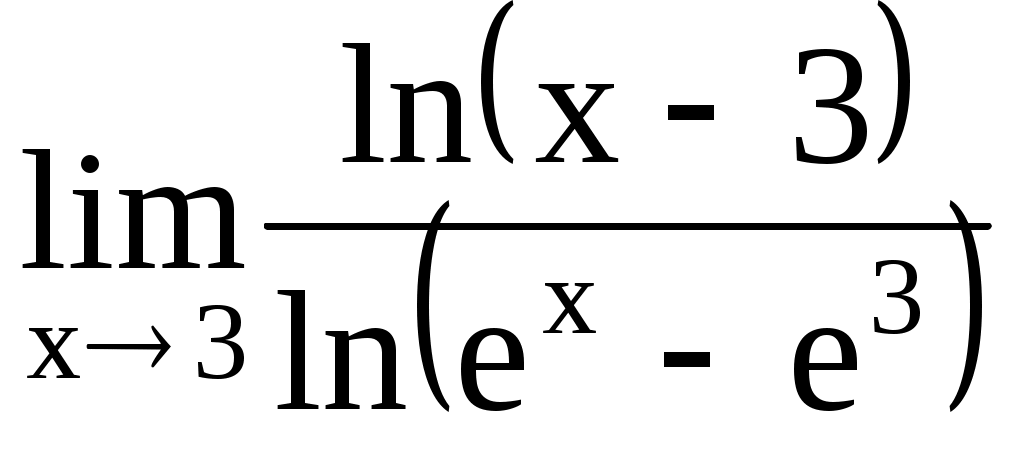 . 4.204.
. 4.204. 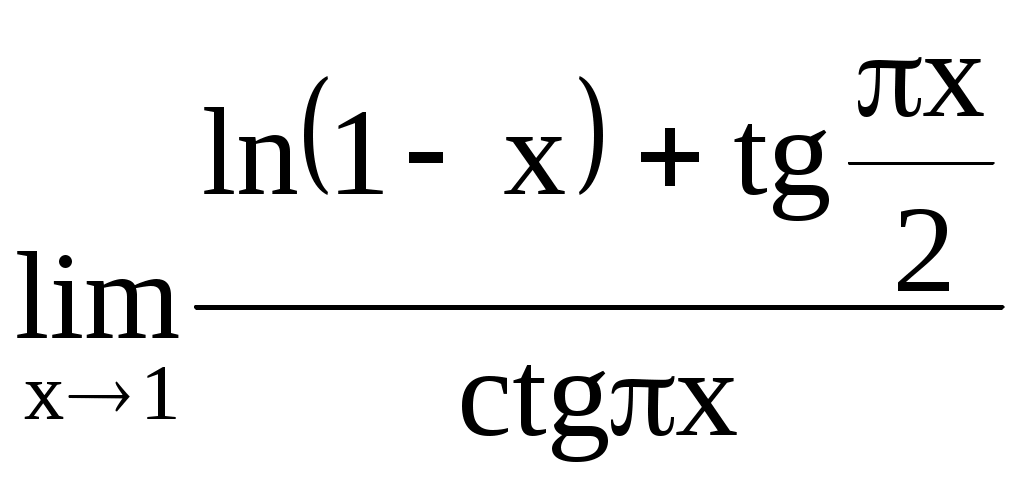 .
.
4.205.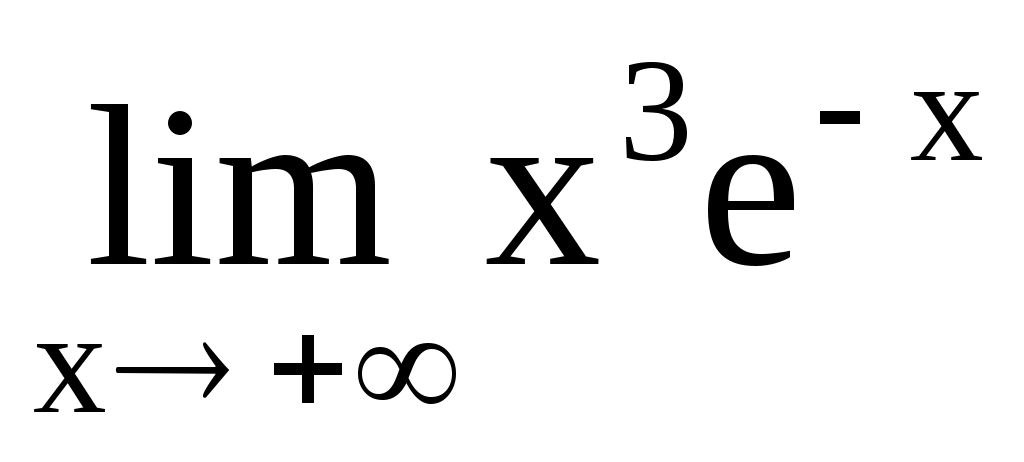 . 4.206.
. 4.206. 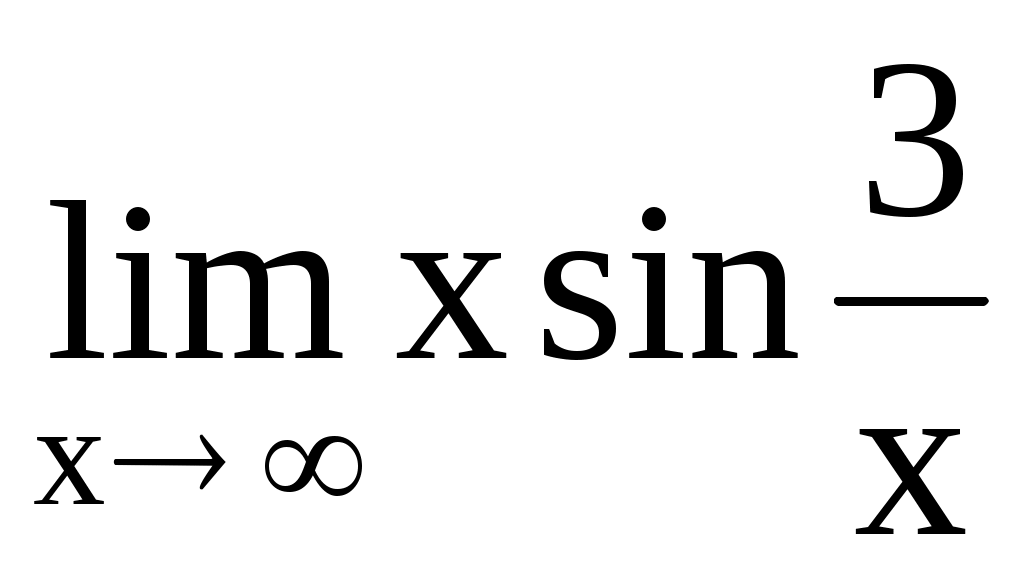 .
.
4.207.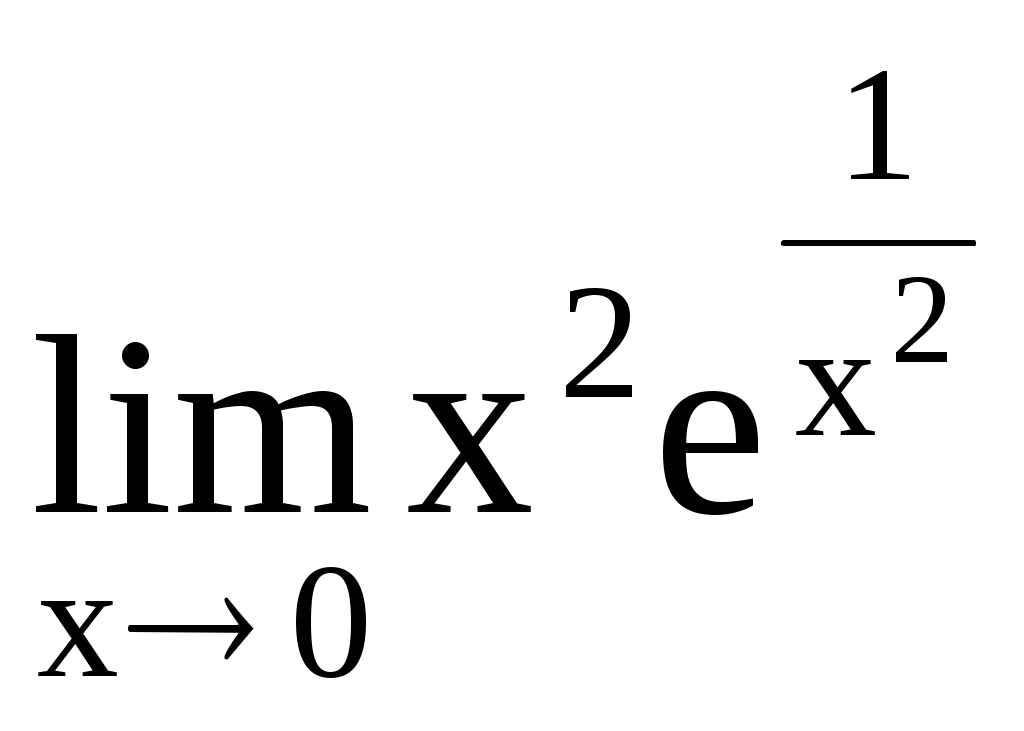 . 4.208.
. 4.208. 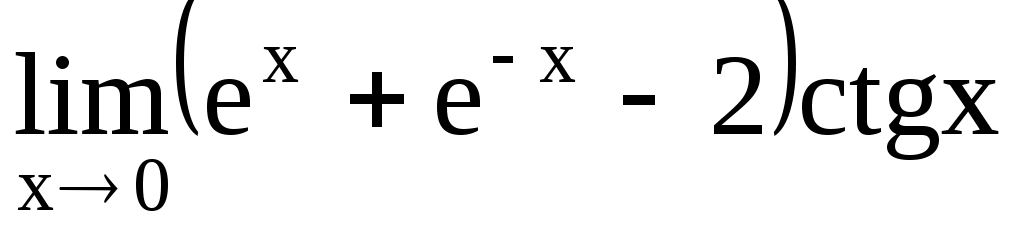 .
.
4.209.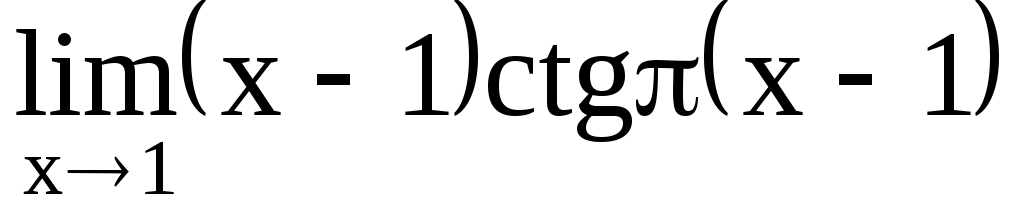 . 4.210.
. 4.210. 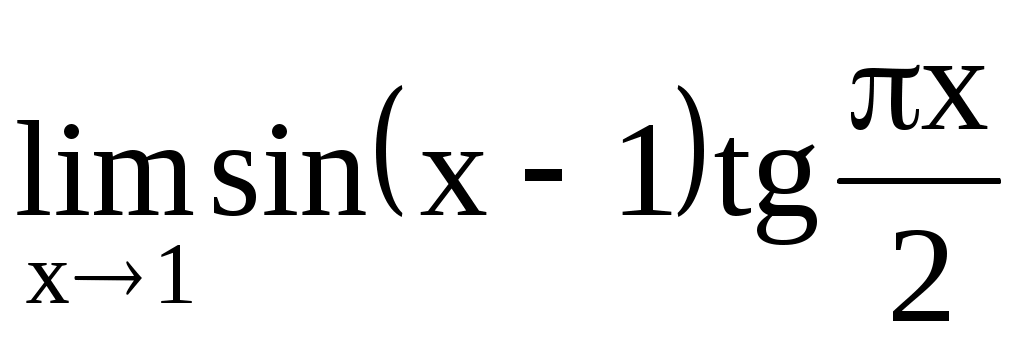 .
.
4.211.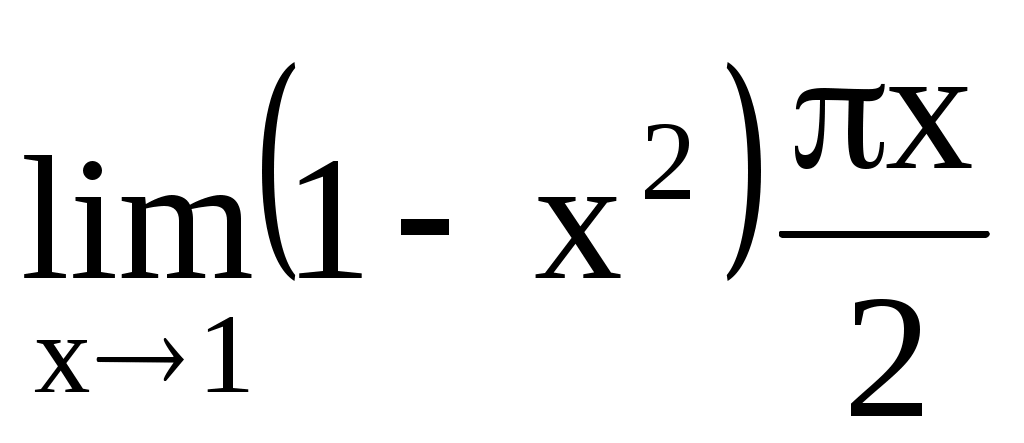 . 4.212.
. 4.212. 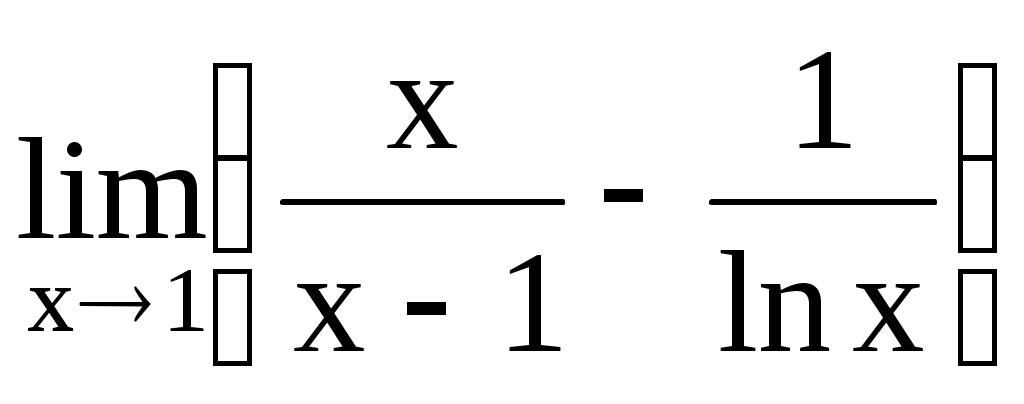 .
.
4.213.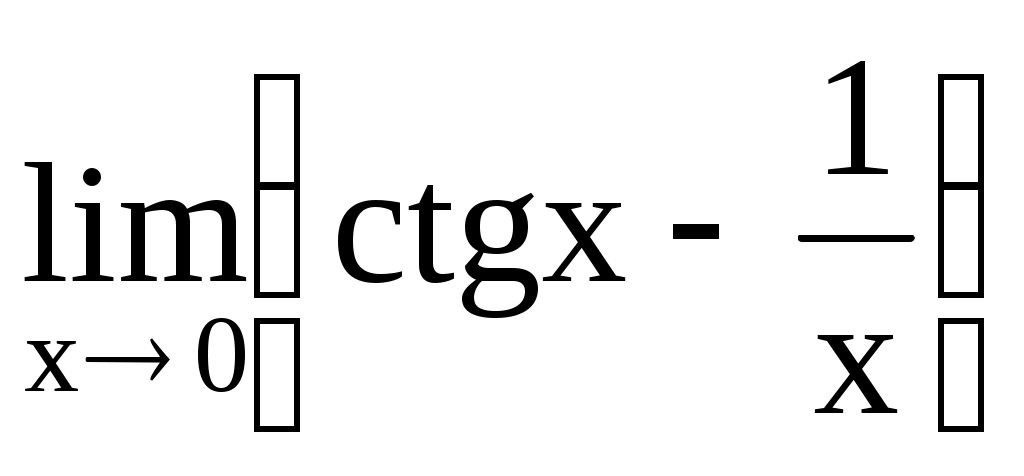 . 4.214.
. 4.214. 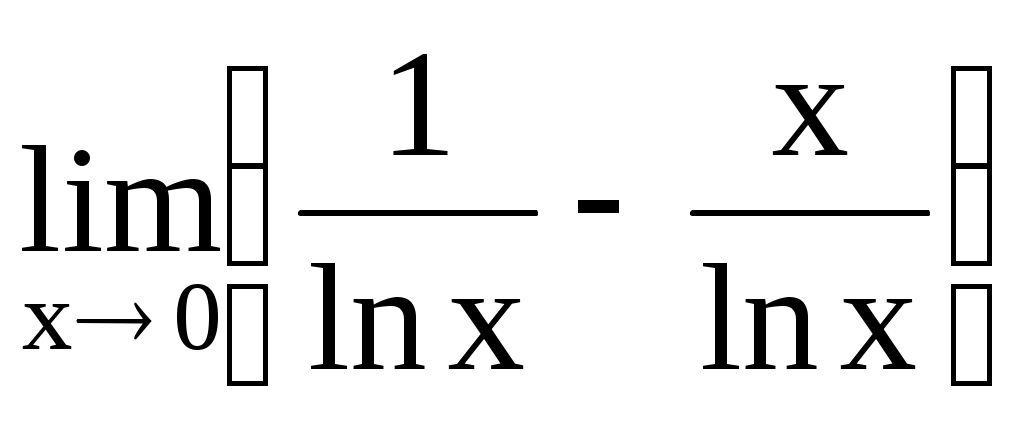 .
.
4.215.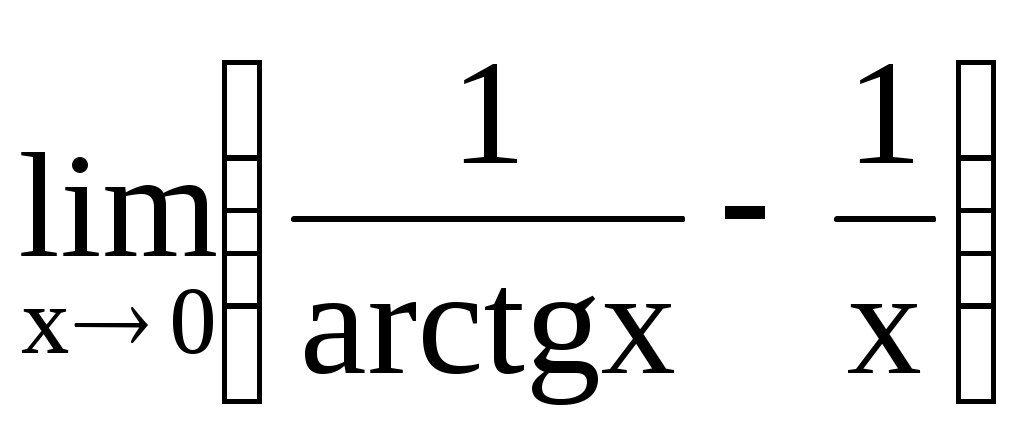 . 4.216.
. 4.216. 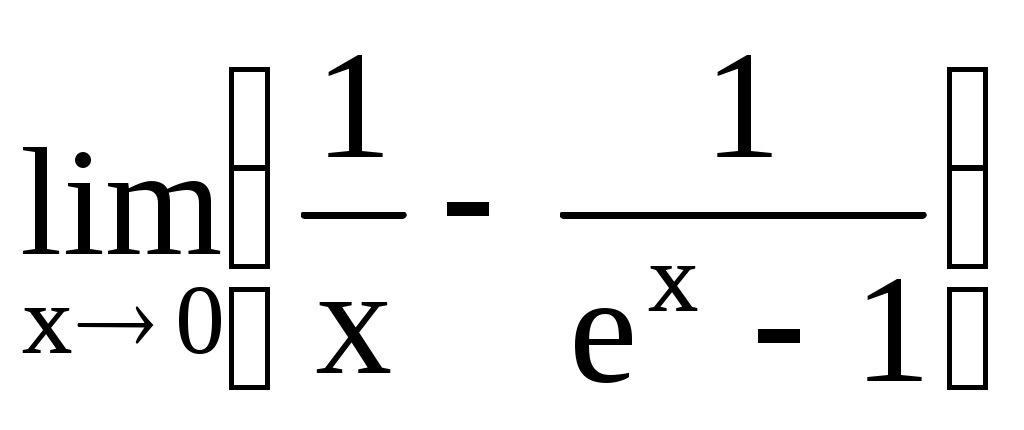 .
.
4.217.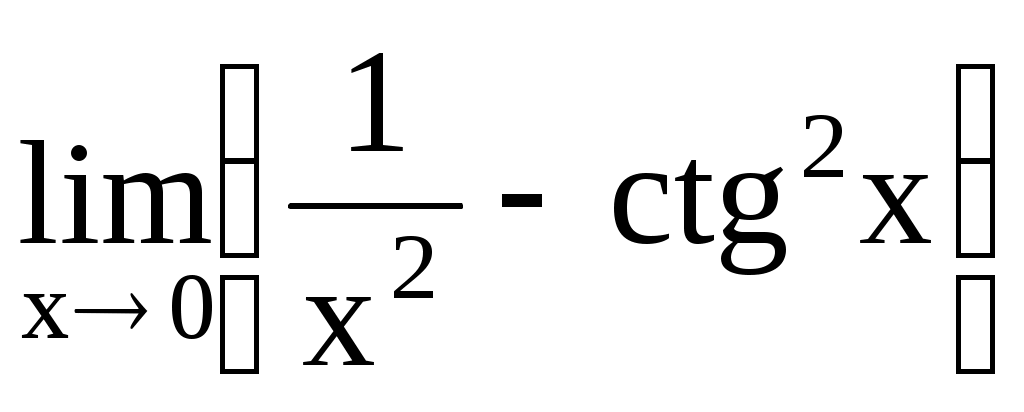
4)
Функции, заданные в неявном виде
4.136.
4.137.
4.138.
4.139.
4.140.
В задачах 4.141–4.151 для функций, заданных параметрически, найти
4.141.
4.143.
4.145.
;
4.147.
4.149.
4.151.
4.153.
4.154.
4.155. Для заданных функций найти дифференциалы 2-го порядка:
1)
4)
В задачах 4.156–4.170 найти наибольшее и наименьшее значения заданных функций в указанных промежутках.
4.156.
; [–2; 2]. 4.157.
4.158.
4.160.
4.162.
4.164.
4.166.
4.168.
4.170.
Задачи на отыскание наибольших и наименьших значений функций
4.171. Число 8 разбить на два таких слагаемых, чтобы сумма их кубов была наименьшей.
4.172. Число 36 разложить на два таких множителя, чтобы сумма их квадратов была наименьшей.
4.173. Из углов квадратного листа картона размером 1818 см2, нужно вырезать одинаковые квадраты так, чтобы согнув лист, получить коробку наибольшей вместимости. Какова должна быть сторона вырезаемого квадрата?
4.174. Открытый чан имеет форму цилиндра. При данном объёме V каковы должны быть радиус основания и высота цилиндра
, чтобы его поверхность была наименьшей.
4.175. Требуется изготовить коническую воронку с образующей, равной 20 см. Какова должна быть высота воронки, чтобы её объём был наибольшим.
4.176. Найти высоту цилиндра наибольшего объёма, который можно вписать в шар радиуса R.
4.177. Найти высоту конуса наибольшего объёма, который можно вписать в шар радиуса R.
4.178. Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
4.179. Бревно длиной в 20 м имеет форму усечённого конуса, диаметры оснований которого равны соответственно 2 и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна и объём которой был бы наибольшим. Каковы должны быть размеры балки?
4.180. Катер стоит на якоре в 9 км от ближайшей точки берега; с катера нужно послать гонца в лагерь, расположенный в 15 км, считая по берегу от ближайшей к катеру точки берега (лагерь расположен на берегу). Если гонец может делать пешком по 5 км/ч, а на вёслах по 4 км/ч, то в каком пункте берега он должен пристать, чтобы попасть в лагерь в кратчайшее время?
4.181. Картина в 1,4 м высотой повешена на стену так, что её нижний край на 1,8 м выше глаза наблюдателя. На каком расстоянии от стены должен стать наблюдатель, чтобы его положение было наиболее благоприятным для осмотра картины (т.е. чтобы угол зрения был наибольшим)?
4.182. На странице книги печатный текст должен занимать S квадратных сантиметров. Верхние и нижние поля должны быть по а см, правое и левое по b см. Если принимать во внимание только экономию бумаги, то какими должны быть наиболее выгодные размеры страницы?
В задачах 4.183–4.232 вычислить пределы, пользуясь правилом Лопиталя.
4.183.
4.185.
4.187.
4.189.
.
4.191.
4.193.
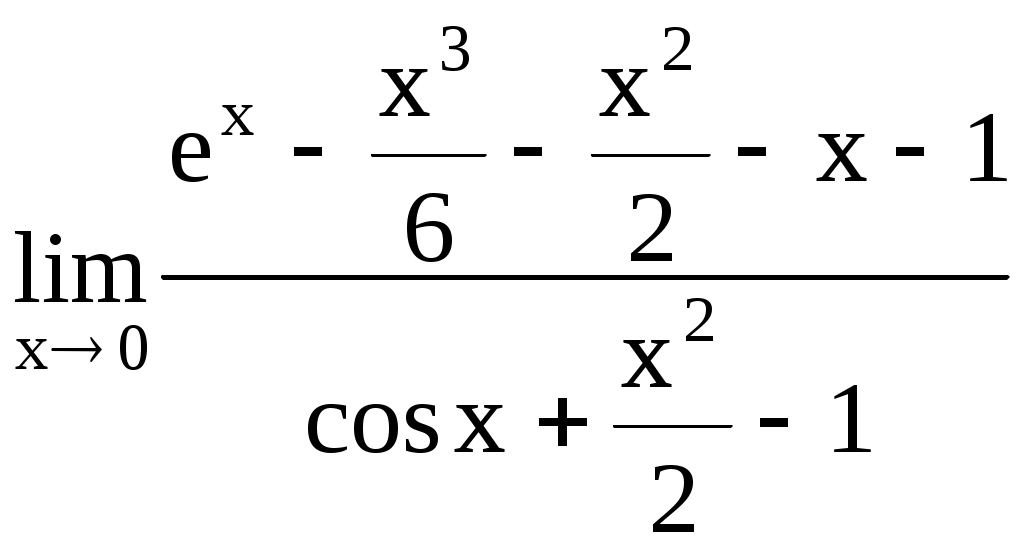 .
.4.195.
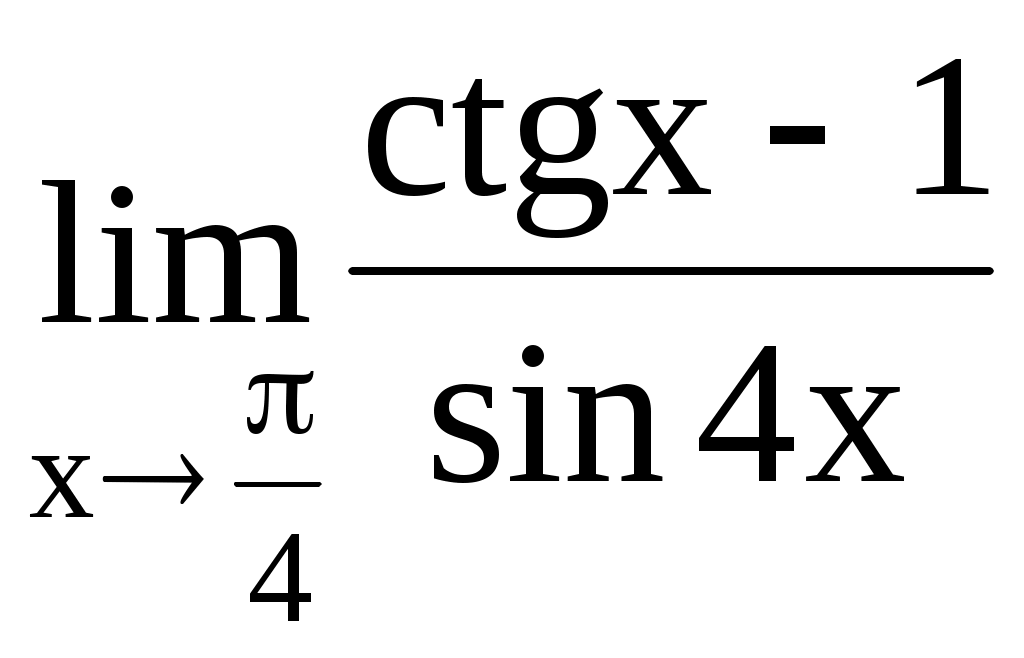 .
.4.197.
4.199.
4.201.
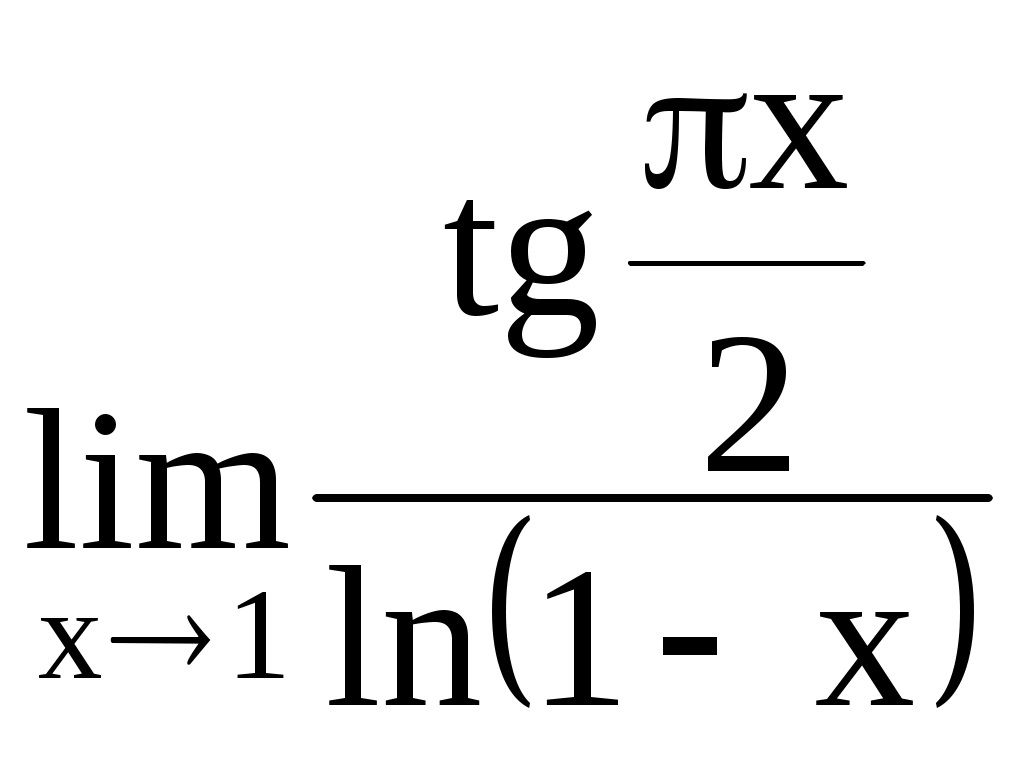 .
.4.203.
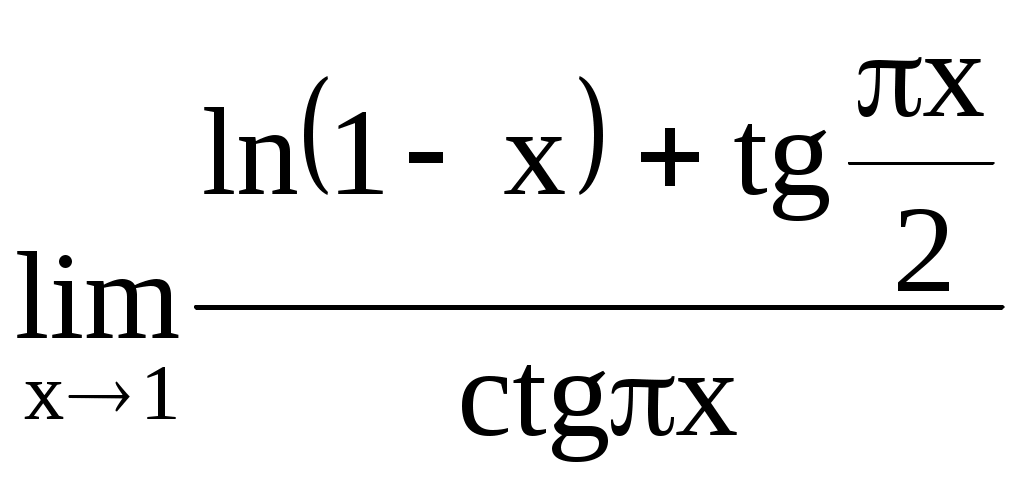 .
.4.205.
4.207.
4.209.
4.211.
4.213.
4.215.
4.217.