Федеральное агентство связи

Ордена Трудового Красного Знамени федерального государственного

бюджетного образовательного учреждения высшего образования

«Московский технический университет связи и информатики»

Волго-Вятский филиал


Кафедра инфокоммуникационных и общепрофессиональных дисциплин (ИКиОПД)
Общая теория связи
Лабораторная работа № 4
«Исследование спектрального анализа и синтеза периодических сигналов»
Методические указания и задания

Выполнил:

Проверил: Чернявский А.Д.

Нижний Новгород 2021


Цель работы. Приобретение навыков спектрального анализа и синтеза периодических сигналов.

Теоретическая часть

В общем случае периодический сигнал s(t) описывается соотношением



где T – постоянная величина, называемая периодом, с;

n – любое целое число (положительное или отрицательное).

Периодический сигнал s(t) может быть разложен в ряд Фурье. Чтобы такое разложение существовало, фрагмент сигнала s(t) длительностью в один период должен удовлетворять условиям Дирихле:

• 
  не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции);
  
• 
  число разрывов первого рода (скачков) должно быть конечным;
  
• 
  число экстремумов должно быть конечным (в качестве примера функции, которая на конечном интервале имеет бесконечное число экстремумов, можно привести sin(l/x) в окрестности нуля).
  

Различают три формы записи ряда Фурье: синусно-косинусная форма, вещественная форма и комплексная форма.

Синусно-косинусная форма ряда Фурье имеет следующий вид:



где k = 1, 2, …, ∞ – номер гармоники спектра Фурье периодического сигнала;

ω1 = 2π/T – основная круговая частота периодического сигнала (частота первой гармоники), рад/с;

---

kω1 – круговая частота k-й гармоники, рад/с;

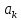– коэффициент k-й «косинусной» составляющей спектра Фурье
периодического сигнала, В;

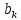– коэффициент k-й «синусной» составляющей спектра Фурье периодического сигнала, В;

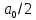– постоянная составляющая спектра Фурье периодического
сигнала, представляющая собой среднее значение сигнала на периоде, В.
Использованные в (2.2) коэффициенты 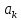, 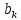(k = 1, 2, …, ∞) и 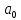определяются по формулам: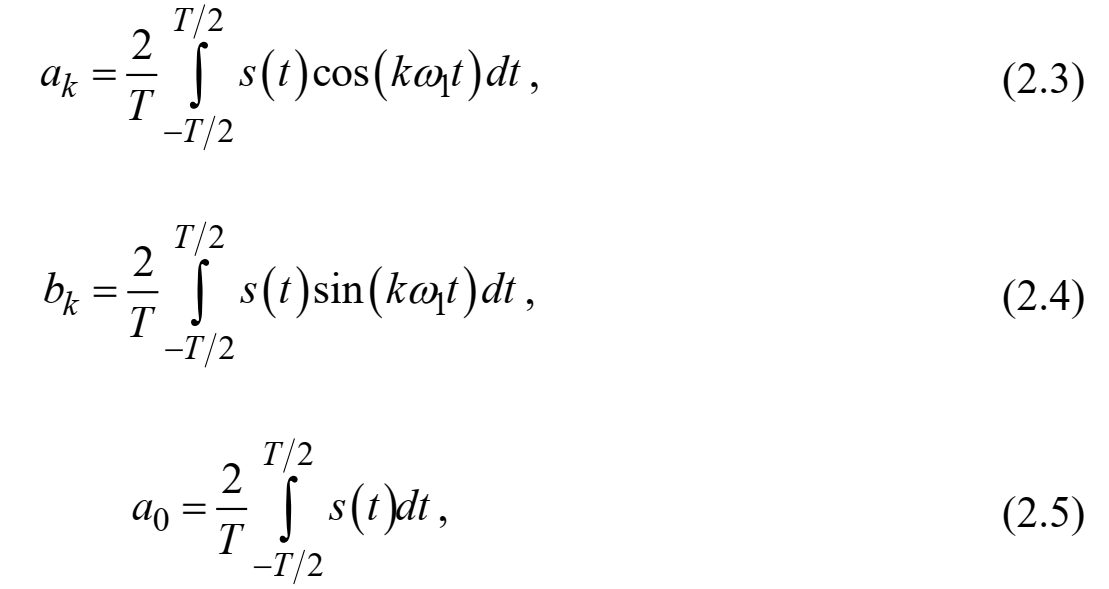


Примечание – Пределы интегрирования в формулах (2.3) – (2.5) не обязательно должны быть от –T/2 до T/2. Интегрирование может производиться по любому интервалу длиной T, результат от этого не изменится. Конкретные пределы выбираются из соображений удобства вычислений; например, может оказаться удобнее выполнять интегрирование от 0 до T или от – T до 0.

На основе анализа (2.2) видно, что базисные функции синусно-косинусной формы ряда Фурье можно представить в виде:



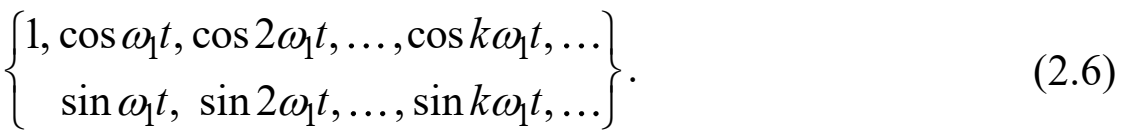
Примечание – Все функции системы (2.6) попарно ортогональны на интервале (–T/2; T/2) или (0; T), а частоты косинусоидальных и синусоидальных составляющих образуют арифметическую прогрессию.

Таким образом, в общем случае спектр периодического сигнала s(t) при использовании синусно-косинусной формы ряда Фурье состоит из постоянной составляющей 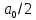и бесконечного множеств коэффициентов {ak}, {bk} (k = 1, 2, …, ∞) при «косинусных» и «синусных» составляющих спектра.

В частном случае, если сигнал s(t) является четной функцией, то все коэффициенты 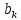будут равны нулю и, в формуле ряда Фурье будут присутствовать только «косинусные» слагаемые.

Если сигнал s(t) является нечетной функцией, равны нулю будут, наоборот, косинусные коэффициенты

---

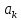
, и в формуле останутся лишь «синусные» слагаемые.

Некоторое неудобство синусно-косинусной формы ряда Фурье состоит в том, что для каждого значения индекса суммирования k в формуле (2.2) фигурируют два слагаемых – синус и косинус.

Поскольку справедливо соотношение:



где 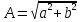– амплитуда гармонического сигнала, В; 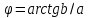– начальная фаза гармонического сигнала, радианы или градусы, то ряд (2.2) можно также представить в компактной форме: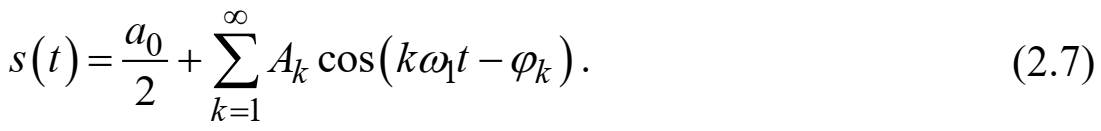


Формула (2.7) представляет вещественную форму записи ряда Фурье. Если сигнал s(t) является четной функцией, фазы 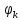могут принимать только значения 0 и π, а если s(t) – функция нечетная, то возможные значения для фазы равны ±π/2.

Обратный переход от вещественной к синусно-косинусной форме записи ряда Фурье осуществляется на основе соотношений:



Сравнивая между собой вещественную к синусно-косинусную форму записи ряда Фурье, отметим, что:

- при использовании синусно-косинусной формы разложения периодического сигнала в тригонометрический ряд (2.2) коэффициенты и зависят от выбора начала отсчета, а при пользовании вещественной формы разложения (2.7) амплитуды гармоник Ak не зависят от выбора начала отсчета и определяются только видом сигнала s(t), а аргументы гармоник 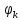зависят от начала отсчета при выборе пределов интегрирования в формулах (2.3) – (2.5);

- при сдвиге начала отсчета вдоль оси времени t на 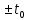амплитуды Ak сохраняются, а фазы 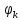получают приращение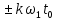

---

(теорема сдвига).

Комплексная форма представления ряда Фурье является наиболее общей и получается из вещественной формы представлением косинуса в виде полусуммы комплексных экспонент (такое представление вытекает из формулы Эйлера)



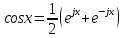
Применив данное преобразование к вещественной форме ряда Фурье, получим суммы комплексных экспонент с положительными и отрицательными показателями:



Будем трактовать экспоненты со знаком «минус» в показателе как члены ряда с отрицательными номерами. В рамках этого же общего подхода постоянное слагаемое 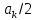станет членом ряда с нулевым номером. В результате получится комплексная форма записи ряда Фурье:



Комплексные коэффициенты ряда 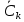связаны с амплитудами Ak и фазами , фигурирующими в вещественной форме записи ряда Фурье (2.7), следующими соотношениями:



Несложно выглядят и формулы связи 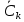с коэффициентами и синусно-косинусной формы ряда Фурье (2.2):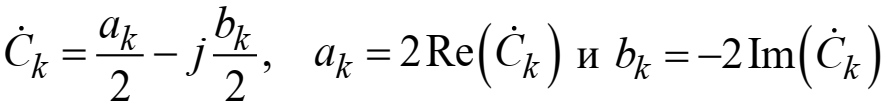



Отсюда сразу же следует и формула непосредственного расчета коэффициентов 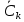ряда Фурье в комплексной форме: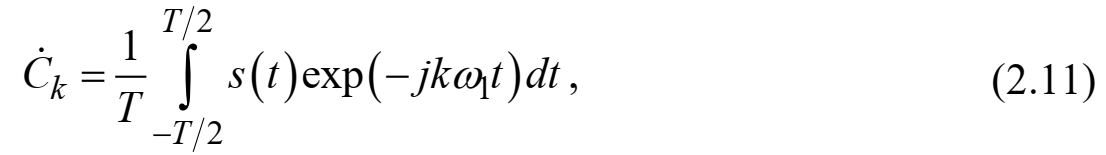



где k – любое целое число.

Формула (2.11) определяет комплексный спектр периодического сигнала. Если s(t) является четной функцией, коэффициенты ряда 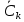будут чисто вещественными, а если s(t) – функция нечетная, коэффициенты ряда окажутся чисто мнимыми.

Совокупность амплитуд гармоник ряда Фурье часто называют амплитудным спектром периодического сигнала (спектр), а совокупность их фаз – фазовым спектром периодического сигнала (таблица 2.1).

---

Если анализируемый сигнал s(t) является вещественным, то его амплитудный и фазовый спектры обладают соответственно четной и нечетной симметрией:



а коэффициенты комплексного ряда Фурье – комплексно-сопряженной симметрией:



где * – символ математической операции комплексного сопряжения.

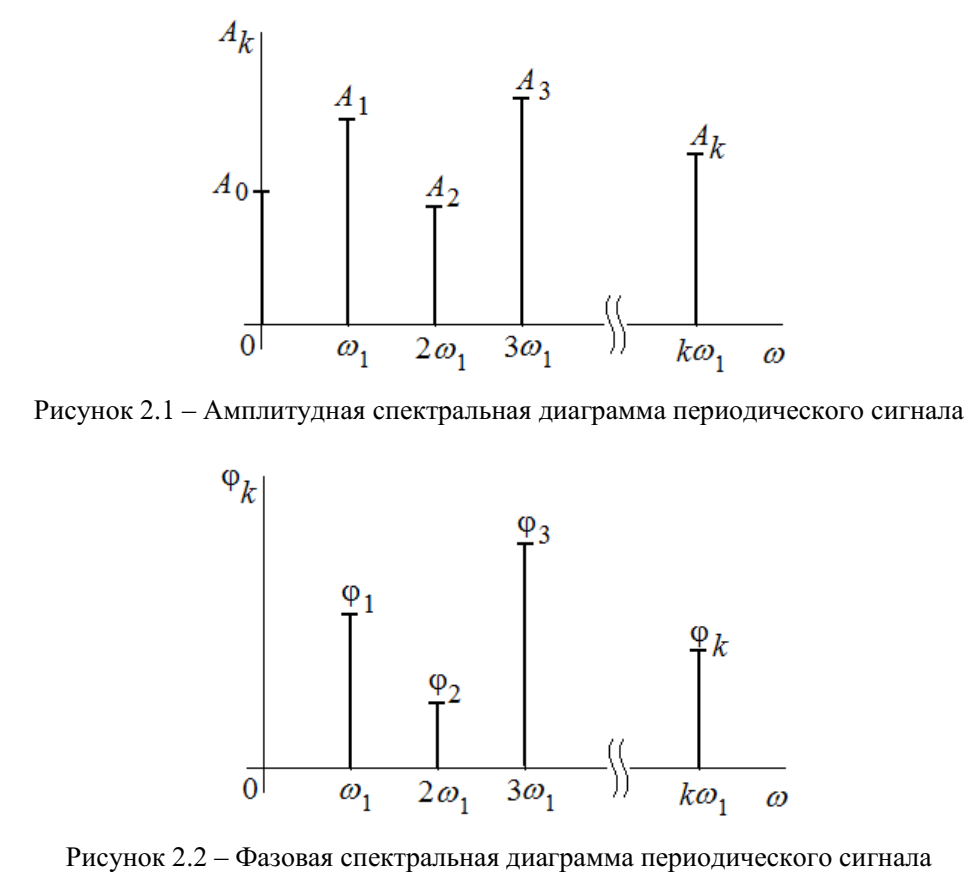
Спектральной диаграммой периодического сигнала принято называть графическое изображение коэффициентов ряда Фурье для заданного сигнала.

Различают амплитудные и фазовые спектральные диаграммы (рисунки 2.1 и 2.2).

Сформулируем основные свойства спектральных диаграмм периодических сигналов:

- первое свойство спектров, изображенных на рисунках 2.1 и 2.2, состоит в том, спектральные диаграммы периодического сигнала являются дискретными функциями частоты, поэтому их называют также линейчатым.

- второе свойство спектров, изображенных на рисунках 2.1 и 2.2, состоит в том, что эти спектры являются гармоническими. Это значит, что они состоит из равноотстоящих спектральных линий, т. к. частоты гармоник находятся в простых кратных соотношениях (все гармоники спектра имеют частоты 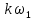кратные частоте первой гармоники ).


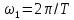Примечание – Конечно, отдельные гармоники, иногда даже первая, могут отсутствовать, т. е. амплитуды их могут равняться нулю, но это, однако, не нарушает гармоничности спектра.

Итак, ряд Фурье представляет данный периодический сигнал s(t) суммой гармонических колебаний (синусоид и косинусоид) кратных частот с соответствующим образом подобранными амплитудами и фазами. Если ограничится конечным числом членов ряда (2.2) и (2.7), то получим периодический сигнал

---

Смотрите также файлы

• Установите последовательность, отражающую систематическое положение вида Сосна обыкновенная в классификации растений, начиная с наименьшей группы.docx

• Как Вы считаете, соответствует ли изображенная ниже игрушка требованиям безопасности Аргументируйте свою точку зрения.docx

• Олимпиада по математике 2 класс i тур.docx

• Текст не нужен Текст не нужен.docx

• Протокол от согласовано Общешкольным родительским советом мбоусош7 им П. Н. Степаненко.doc