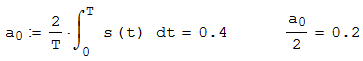Файл: Лабораторная работа 4 Исследование спектрального анализа и синтеза периодических сигналов Методические указания и задания.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 98
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
являющийся приближенным изображением сигнала 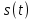 :
:
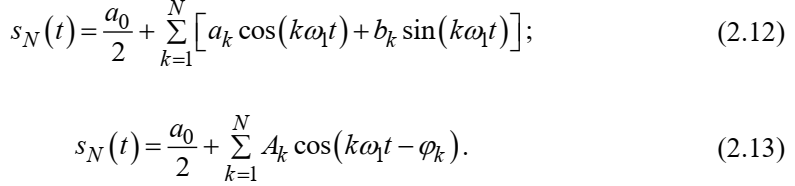
С увеличением числа членов N приближение, разумеется, улучшается, и в пределе, при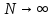 приближенные равенства (2.12) и (2.13) переходят в точные (2.2) и (2.7), соответственно.
приближенные равенства (2.12) и (2.13) переходят в точные (2.2) и (2.7), соответственно.
При этом существенно, что приближения (2.12) и (2.13) есть всегда наилучшие приближения для любого N, т. е. когда возникает необходимость аппроксимировать периодическую функцию тригонометрическим полиномом, то наименьшее квадратичное отклонение получится, если коэффициенты полинома будут определены по формулам (2.3) – (2.5).
Известно, что если существует интеграл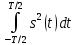 , то средняя квадратическая погрешность
, то средняя квадратическая погрешность
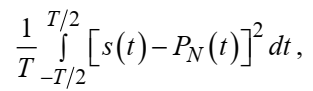
где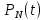 – произвольный тригонометрический многочлен вида
– произвольный тригонометрический многочлен вида
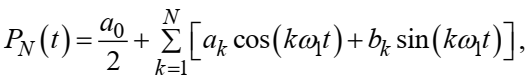
при каждом N принимает наименьшее значение, когда в качестве коэффициентов и
и  многочлена
многочлена 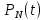 берутся соответствующие коэффициенты Фурье (2.3) – (2.5)
берутся соответствующие коэффициенты Фурье (2.3) – (2.5)  и
и  функции s(t), т. е. когда тригонометрический многочлен
функции s(t), т. е. когда тригонометрический многочлен 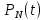 есть частичная сумма
есть частичная сумма
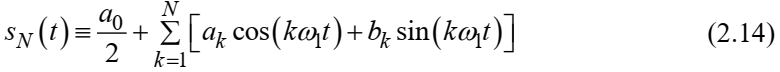
ряда Фурье функции s(t) .
Следует учитывать, что при усечении рядов Фурье определенное искажение функций существует всегда. Но при малой доле энергии отсекаемой части сигнала (при быстром затухании спектров функций с ростом номера гармоники) этот эффект, получивший название эффекта Гиббса, может быть и малозаметен. На скачках и разрывах функций эффект Гиббса проявляется наиболее ярко, что может весьма существенно сказаться на качестве и точности обработки сигналов:
- крутизна перепадов «размывается», т. к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (2.12) или (2.13);
- по обе стороны «размытых» перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ряда (2.12) или (2.13).
Более подробно проявление эффекта Гиббса будет рассмотрено далее в примере спектрального анализа и синтеза периодической последовательности прямоугольных импульсов.
Теорема Парсеваля. Определив среднюю мощность сигнала s(t), представленного в виде ряда Фурье (2.2), за период колебаний T, получим:
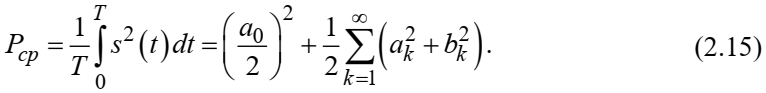
При выводе формулы (2.15) использовано соотношение
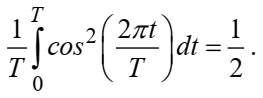
Соотношение (2.15) представляет собой математическую запись теоремы Парсеваля, из которой следует, что если периодический сигнал s(t)разлагается в ряд Фурье, то средняя за период мощность этого сигнала заключается в сумме мощностей постоянной составляющей и гармоник спектра Фурье.
При использовании вещественной формы записи ряда Фурье (2.7) равенство Парсеваля (2.15) можно, также переписать в виде
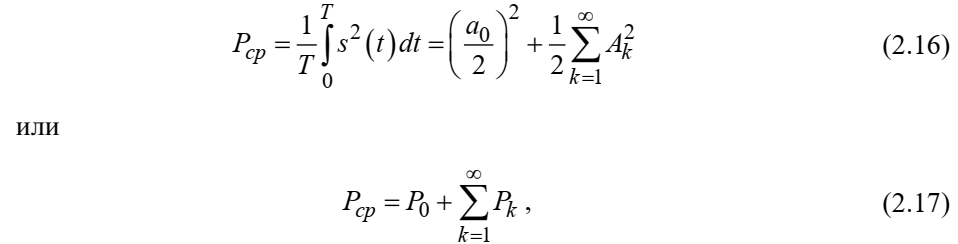

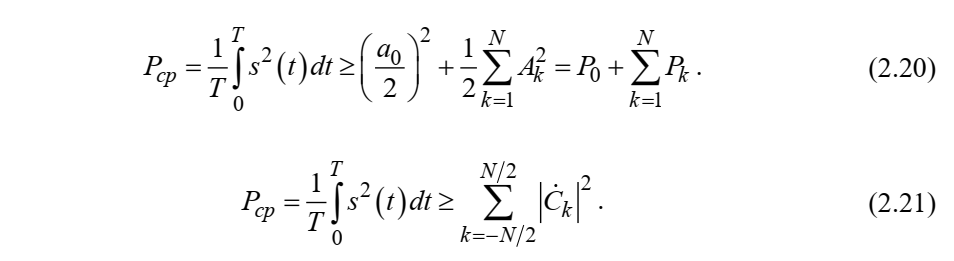
Оборудование и материалы
Для выполнения лабораторной работы необходим персональный компьютер. Также необходима операционная система WINDOWS , программа MathCAD 13 и выше.
Указания по технике безопасности
При выполнении лабораторной работы запрещается:
- самостоятельно производить ремонт персонального компьютера, а также установку и удаление имеющегося программного обеспечения;
- нарушать общепринятые правила техники безопасности при работе с электрооборудованием, в частности, касаться электрических розеток металлическими предметами и т.д.;
- принимать пищу, напитки и сорить на рабочем месте пользователя персонального компьютера.
В случае неисправности персонального компьютера необходимо немедленно сообщить об этом обслуживающему персоналу лаборатории (системному администратору, оператору).
Указания по порядку выполнения работы
Методику выполнения работы рассмотрим на примере спектрального анализа и синтеза в усеченном базисе Фурье (ограничиться рассмотрением десяти гармоник т. е. N =10) периодической последовательности прямоугольных импульсов с высотой A = 1 В, длительностью τ = 0,2 с и периодом Т = 1 с (рисунок 2.3).
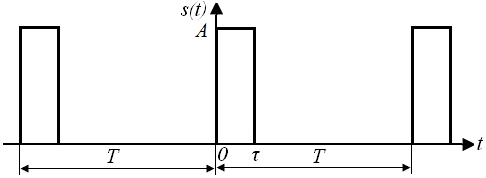
Рис.2.3. Периодическая последовательность прямоугольных импульсов
Требуется для сигнала s(t) определить:
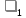 – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;
– основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;
 – коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала, В;
– коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала, В;
 – коэффициент k-той синусной составляющей спектра Фурье периодического сигнала, В;
– коэффициент k-той синусной составляющей спектра Фурье периодического сигнала, В;
 – постоянную составляющую спектра Фурье периодического сигнала, В;
– постоянную составляющую спектра Фурье периодического сигнала, В;
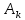 – амплитуду k-той гармоники спектра Фурье периодического сигнала, В;
– амплитуду k-той гармоники спектра Фурье периодического сигнала, В;
 – начальную фазу k-той гармоники спектра Фурье периодического сигнала, радианы или градусы;
– начальную фазу k-той гармоники спектра Фурье периодического сигнала, радианы или градусы;
- амплитудную и фазовую спектральные диаграммы периодического сигнала (построить линейчатые спектры);
- восстановленный по усеченному ряду Фурье сигнал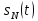 являющийся приближенным изображением сигнала s(t);
являющийся приближенным изображением сигнала s(t);
- расстояние и квадрат расстояния между сигналами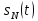 и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t);
и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t);
- среднюю мощность сигнала s(t) за период колебаний T;
- сумму мощностей постоянной составляющей и гармоник спектра Фурье,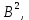 и выполнение неравенства Парсеваля;
и выполнение неравенства Парсеваля;
- tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал принимает максимальное значение (исследование эффекта Гиббса), с;
принимает максимальное значение (исследование эффекта Гиббса), с;
- Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса, В;
- Δ% – максимальное значение относительной ошибки восстановления сигнала, выраженное в процентах, обусловленное наличием эффекта Гиббса;
- исследовать, как влияет изменение количества гармоник усеченного ряда Фурье на изменение параметров эффекта Гиббса – tm, Δ и Δ%.
Рассмотрим решение поставленной задачи в математическом пакете Mathcad.
В приводимом ниже документе Mathcad приняты следующие обозначения:
- s(t) – функция, описывающая зависимость отдельного импульса, составляющего периодическую последовательность импульсов, от текущего времени в пределах одного периода T;
- sN(t) – периодическая функция, восстановленная (спектральный синтез) по результатам спектрального анализа (разложению в ряд Фурье) функции s(t) по N гармоникам;
- T – период, с;
- τ – длительность импульсов, с;
- A – высота импульса, В;
- N – число рассчитываемых гармоник спектра периодической последовательности импульсов (задача спектрального анализа);
-
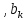 , – коэффициент k-той косинусной и синусной составляющей спектра Фурье периодического сигнала (формула (2.2)), k = 1, 2, 3, ... , N;
, – коэффициент k-той косинусной и синусной составляющей спектра Фурье периодического сигнала (формула (2.2)), k = 1, 2, 3, ... , N;
-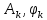 – амплитуда и начальная фаза k-той гармоники спектра Фурье периодического сигнала (формула (2.7)), k = 1, 2, 3, ... , N;
– амплитуда и начальная фаза k-той гармоники спектра Фурье периодического сигнала (формула (2.7)), k = 1, 2, 3, ... , N;
-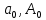 , – удвоенное значение постоянной составляющей спектра Фурье периодического сигнала (формулы (2.2) и (2.7));
, – удвоенное значение постоянной составляющей спектра Фурье периодического сигнала (формулы (2.2) и (2.7));
- tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал sN(t) принимает максимальное значение (исследование эффекта Гиббса);
- Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса;
- Δ% – максимальное значение относительной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса;
Решение:
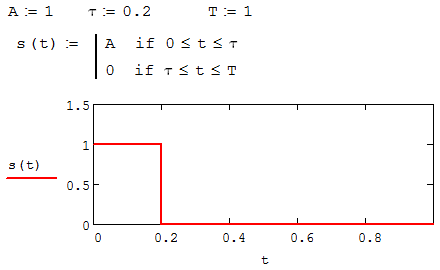
Рисунок 2.4 – Определение и график сигнала s(t) в пределах одного периода
2. Вычисляем основную круговую частоту периодического сигнала
(частоту первой гармоники), рад/с, (рисунок 2.5).
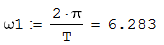
Рисунок 2.5 – Вычисляем основную круговую частоту периодического
сигнала (частоту первой гармоники)
Как видно из рисунка 2.5, частота первой гармоники составляет 6,283 рад/с.
3.Задаем количество гармоник усеченного ряда Фурье (N = 10), формируем ранжированную переменную k (k = 0, 1, 2, … , 10) и вычисляем коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала (рисунок 2.6).
k-той косинусной составляющей спектра Фурье периодического сигнала (рисунок 2.6).

Рисунок 2.6 – Вычисляем коэффициент k-той косинусной составляющей
спектра Фурье периодического сигнала
4. Вычисляем коэффициент k-той синусной составляющей спектра Фурье периодического сигнала (рисунок 2.7).
k-той синусной составляющей спектра Фурье периодического сигнала (рисунок 2.7).
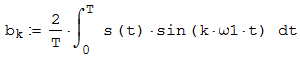
Рисунок 2.7 – Вычисляем коэффициент k-той синусной составляющей спектра Фурье периодического сигнала
5. Отображаем в виде векторов рассчитанные значения коэффициентов
 (рисунок 2.8).
(рисунок 2.8).
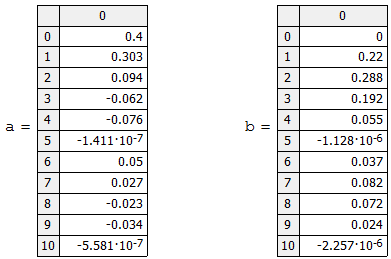
Рисунок 2.8 – Рассчитанные значения коэффициентов

6. Вычисляем постоянную составляющую спектра Фурье периодического сигнала (рисунок 2.9).
спектра Фурье периодического сигнала (рисунок 2.9).
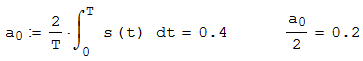
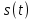 :
:
С увеличением числа членов N приближение, разумеется, улучшается, и в пределе, при
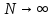 приближенные равенства (2.12) и (2.13) переходят в точные (2.2) и (2.7), соответственно.
приближенные равенства (2.12) и (2.13) переходят в точные (2.2) и (2.7), соответственно.При этом существенно, что приближения (2.12) и (2.13) есть всегда наилучшие приближения для любого N, т. е. когда возникает необходимость аппроксимировать периодическую функцию тригонометрическим полиномом, то наименьшее квадратичное отклонение получится, если коэффициенты полинома будут определены по формулам (2.3) – (2.5).
Известно, что если существует интеграл
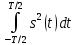 , то средняя квадратическая погрешность
, то средняя квадратическая погрешность 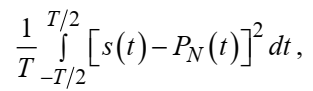
где
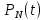 – произвольный тригонометрический многочлен вида
– произвольный тригонометрический многочлен вида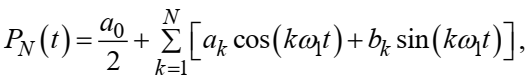
при каждом N принимает наименьшее значение, когда в качестве коэффициентов
 и
и  многочлена
многочлена 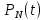 берутся соответствующие коэффициенты Фурье (2.3) – (2.5)
берутся соответствующие коэффициенты Фурье (2.3) – (2.5)  и
и  функции s(t), т. е. когда тригонометрический многочлен
функции s(t), т. е. когда тригонометрический многочлен 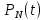 есть частичная сумма
есть частичная суммаряда Фурье функции s(t) .
Следует учитывать, что при усечении рядов Фурье определенное искажение функций существует всегда. Но при малой доле энергии отсекаемой части сигнала (при быстром затухании спектров функций с ростом номера гармоники) этот эффект, получивший название эффекта Гиббса, может быть и малозаметен. На скачках и разрывах функций эффект Гиббса проявляется наиболее ярко, что может весьма существенно сказаться на качестве и точности обработки сигналов:
- крутизна перепадов «размывается», т. к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (2.12) или (2.13);
- по обе стороны «размытых» перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ряда (2.12) или (2.13).
Более подробно проявление эффекта Гиббса будет рассмотрено далее в примере спектрального анализа и синтеза периодической последовательности прямоугольных импульсов.
Теорема Парсеваля. Определив среднюю мощность сигнала s(t), представленного в виде ряда Фурье (2.2), за период колебаний T, получим:
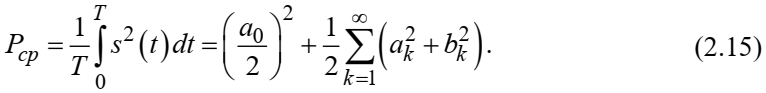
При выводе формулы (2.15) использовано соотношение
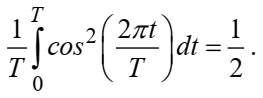
Соотношение (2.15) представляет собой математическую запись теоремы Парсеваля, из которой следует, что если периодический сигнал s(t)разлагается в ряд Фурье, то средняя за период мощность этого сигнала заключается в сумме мощностей постоянной составляющей и гармоник спектра Фурье.
При использовании вещественной формы записи ряда Фурье (2.7) равенство Парсеваля (2.15) можно, также переписать в виде
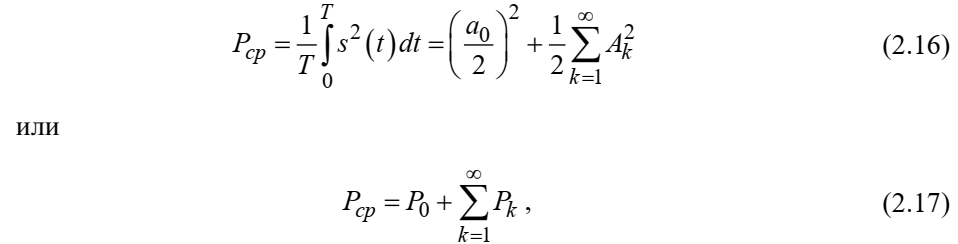

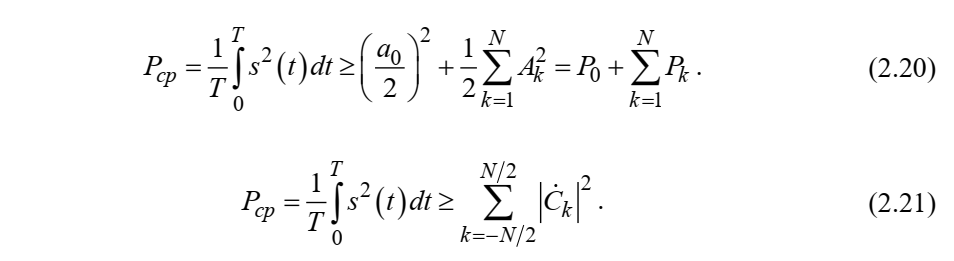
Оборудование и материалы
Для выполнения лабораторной работы необходим персональный компьютер. Также необходима операционная система WINDOWS , программа MathCAD 13 и выше.
Указания по технике безопасности
При выполнении лабораторной работы запрещается:
- самостоятельно производить ремонт персонального компьютера, а также установку и удаление имеющегося программного обеспечения;
- нарушать общепринятые правила техники безопасности при работе с электрооборудованием, в частности, касаться электрических розеток металлическими предметами и т.д.;
- принимать пищу, напитки и сорить на рабочем месте пользователя персонального компьютера.
В случае неисправности персонального компьютера необходимо немедленно сообщить об этом обслуживающему персоналу лаборатории (системному администратору, оператору).
Указания по порядку выполнения работы
Методику выполнения работы рассмотрим на примере спектрального анализа и синтеза в усеченном базисе Фурье (ограничиться рассмотрением десяти гармоник т. е. N =10) периодической последовательности прямоугольных импульсов с высотой A = 1 В, длительностью τ = 0,2 с и периодом Т = 1 с (рисунок 2.3).

Рис.2.3. Периодическая последовательность прямоугольных импульсов
Требуется для сигнала s(t) определить:
 – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;
– основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;
 – коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала, В;
– коэффициент k-той косинусной составляющей спектра Фурье периодического сигнала, В;
 – коэффициент k-той синусной составляющей спектра Фурье периодического сигнала, В;
– коэффициент k-той синусной составляющей спектра Фурье периодического сигнала, В;
 – постоянную составляющую спектра Фурье периодического сигнала, В;
– постоянную составляющую спектра Фурье периодического сигнала, В;
 – амплитуду k-той гармоники спектра Фурье периодического сигнала, В;
– амплитуду k-той гармоники спектра Фурье периодического сигнала, В;
 – начальную фазу k-той гармоники спектра Фурье периодического сигнала, радианы или градусы;
– начальную фазу k-той гармоники спектра Фурье периодического сигнала, радианы или градусы;- амплитудную и фазовую спектральные диаграммы периодического сигнала (построить линейчатые спектры);
- восстановленный по усеченному ряду Фурье сигнал
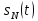 являющийся приближенным изображением сигнала s(t);
являющийся приближенным изображением сигнала s(t);- расстояние и квадрат расстояния между сигналами
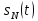 и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t);
и s(t) за период колебаний T, выраженный в процентной мере относительно квадрата нормы сигнала s(t);- среднюю мощность сигнала s(t) за период колебаний T;
- сумму мощностей постоянной составляющей и гармоник спектра Фурье,
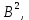 и выполнение неравенства Парсеваля;
и выполнение неравенства Парсеваля;
- tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал
 принимает максимальное значение (исследование эффекта Гиббса), с;
принимает максимальное значение (исследование эффекта Гиббса), с;- Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса, В;
- Δ% – максимальное значение относительной ошибки восстановления сигнала, выраженное в процентах, обусловленное наличием эффекта Гиббса;
- исследовать, как влияет изменение количества гармоник усеченного ряда Фурье на изменение параметров эффекта Гиббса – tm, Δ и Δ%.
Рассмотрим решение поставленной задачи в математическом пакете Mathcad.
В приводимом ниже документе Mathcad приняты следующие обозначения:
- s(t) – функция, описывающая зависимость отдельного импульса, составляющего периодическую последовательность импульсов, от текущего времени в пределах одного периода T;
- sN(t) – периодическая функция, восстановленная (спектральный синтез) по результатам спектрального анализа (разложению в ряд Фурье) функции s(t) по N гармоникам;
- T – период, с;
- τ – длительность импульсов, с;
- A – высота импульса, В;
- N – число рассчитываемых гармоник спектра периодической последовательности импульсов (задача спектрального анализа);
-

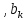 , – коэффициент k-той косинусной и синусной составляющей спектра Фурье периодического сигнала (формула (2.2)), k = 1, 2, 3, ... , N;
, – коэффициент k-той косинусной и синусной составляющей спектра Фурье периодического сигнала (формула (2.2)), k = 1, 2, 3, ... , N;-
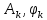 – амплитуда и начальная фаза k-той гармоники спектра Фурье периодического сигнала (формула (2.7)), k = 1, 2, 3, ... , N;
– амплитуда и начальная фаза k-той гармоники спектра Фурье периодического сигнала (формула (2.7)), k = 1, 2, 3, ... , N;-
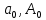 , – удвоенное значение постоянной составляющей спектра Фурье периодического сигнала (формулы (2.2) и (2.7));
, – удвоенное значение постоянной составляющей спектра Фурье периодического сигнала (формулы (2.2) и (2.7));- tm – момент времени, когда восстановленный по усеченному ряду Фурье сигнал sN(t) принимает максимальное значение (исследование эффекта Гиббса);
- Δ – максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса;
- Δ% – максимальное значение относительной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса;
Решение:
-
Запускаем математический пакет Mathcad. Согласно форме сигнала s(t) (таблица 2.3) и заданным параметрам вводим определение сигнала и строим его график в пределах одного периода (рисунок 2.4).

Рисунок 2.4 – Определение и график сигнала s(t) в пределах одного периода
2. Вычисляем основную круговую частоту периодического сигнала
(частоту первой гармоники), рад/с, (рисунок 2.5).
Рисунок 2.5 – Вычисляем основную круговую частоту периодического
сигнала (частоту первой гармоники)
Как видно из рисунка 2.5, частота первой гармоники составляет 6,283 рад/с.
3.Задаем количество гармоник усеченного ряда Фурье (N = 10), формируем ранжированную переменную k (k = 0, 1, 2, … , 10) и вычисляем коэффициент
 k-той косинусной составляющей спектра Фурье периодического сигнала (рисунок 2.6).
k-той косинусной составляющей спектра Фурье периодического сигнала (рисунок 2.6).
Рисунок 2.6 – Вычисляем коэффициент k-той косинусной составляющей
спектра Фурье периодического сигнала
4. Вычисляем коэффициент
 k-той синусной составляющей спектра Фурье периодического сигнала (рисунок 2.7).
k-той синусной составляющей спектра Фурье периодического сигнала (рисунок 2.7).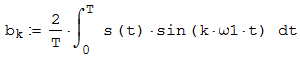
Рисунок 2.7 – Вычисляем коэффициент k-той синусной составляющей спектра Фурье периодического сигнала
5. Отображаем в виде векторов рассчитанные значения коэффициентов

 (рисунок 2.8).
(рисунок 2.8).
Рисунок 2.8 – Рассчитанные значения коэффициентов


6. Вычисляем постоянную составляющую
 спектра Фурье периодического сигнала (рисунок 2.9).
спектра Фурье периодического сигнала (рисунок 2.9).