Рисунок 2.9 – Вычисляем постоянную составляющую спектра Фурье периодического сигнала
Примечание – Строго говоря, можно было повторно и не вычислять постоянную составляющую спектра Фурье периодического сигнала, т. к. удвоенное значение этой составляющей совпадает со значением элемента вектора a (рисунок) при значении индекса k = 0.

7. Вычисляем и отображаем амплитуды , В, и начальные фазы , рад, гармоник спектра Фурье периодического сигнала (рисунок 2.10).

Примечания

- На рисунке 2.10 функция atan2(x,y) возвращает угол, отсчитанный от оси x против хода часовой стрелки до направления на точку с координатами x и y. Результат выражается в радианной мере в диапазоне между –π и π, включая и –π.

- При вычислении начальных фаз гармоник было использовано ограничение на абсолютную величину k-й синусной составляющей спектра Фурье периодического сигнала 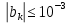т. к. без этого ограничения, например, для пятой гармоники имеем 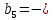1,128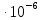 , 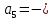1,411 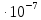и atan2( 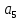, 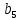)=-1,659 рад или –97,127 градусов, что является ошибкой.


Рисунок 2.10 – Амплитуды и начальные фазы гармоники спектра Фурье периодического сигнала

8. Строим амплитудную и фазовую спектральные диаграммы периодического сигнала (рисунки 2.11 и 2.12).


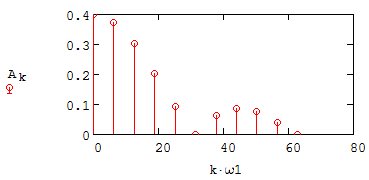
Рисунок 2.11 – Амплитудная спектральная диаграмма периодического сигнала



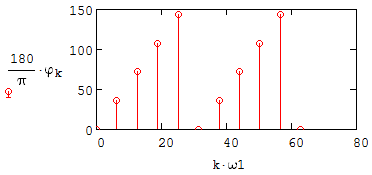
Рисунок 2.12 – Фазовая спектральная диаграмма периодического сигнала

Примечания

- На рисунках 2.11 и 2.12 вдоль оси абсцисс отложена круговая частота k-й гармоники, рад/с;

---

- На рисунке 2.11 вдоль оси ординат отложена амплитуда k-й гармоники, включая и удвоенное значение постоянной составляющей ( 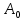) спектра Фурье периодического сигнала в вольтах.

- На рисунке 2.12 вдоль оси ординат отложена начальная фаза k-той гармоники спектра Фурье периодического сигнала в градусах.

9. Находим, восстановленный по усеченному ряду Фурье сигнал , являющийся приближенным изображением сигнала s(t), и строим его временную диаграмму в пределах двух периодов и временную диаграмму исходного сигнала s(t) в пределах, заданного в пределах одного периода (рисунок 2.13).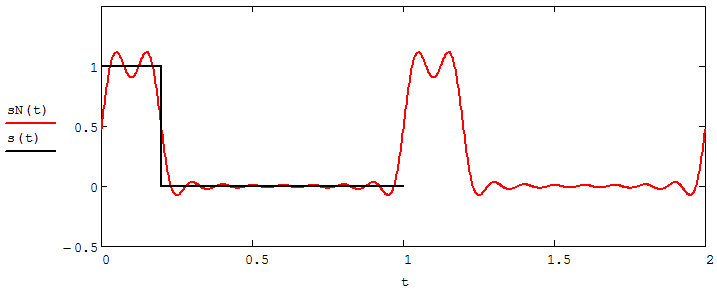



Рисунок 2.13 – Восстановленный по усеченному ряду Фурье сигнал и исходный сигнал s(t), заданный в пределах одного периода
10. Расстояние и квадрат расстояния между сигналами и s(t) за

период колебаний T (рисунок 2.14).



Рисунок 2.14 – Определение расстояния и квадрата расстояния между

сигналами и s(t)

11. Квадрат расстояния между сигналами и s(t) за период колебаний T (рисунок 2.15), выраженный в процентной мере относительно квадрата нормы сигнала s(t).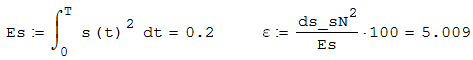



Рисунок 2.15 – Квадрата расстояния между сигналами sN(t ) и s(t ), выраженный в процентной мере относительно квадрата нормы сигнала s(t)
Делаем вывод о том, что если ограничиться рассмотрением десяти гармоник спектра Фурье, то квадрат расстояния между сигналами sN(t) и s(t) составляет примерно 5% относительно квадрата нормы сигнала s(t) .

12. Находим среднюю мощность сигнала s(t) за период колебаний T (рисунок 2.16).



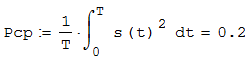
Рисунок 2.16 – Средняя мощность сигнала s(t) за период колебаний T
13. Вычисляем сумму мощностей постоянной составляющей и гармоник спектра Фурье и проверяем выполнение неравенства Парсеваля (рисунок 2.17).

---

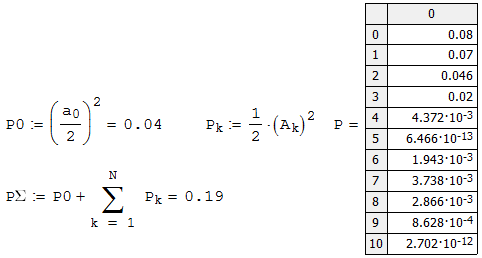
Рисунок 2.17 – Сумма мощностей постоянной составляющей и десяти

гармоник спектра Фурье

Сравнивая между собой Pcp (рисунок 2.16) и PΣ (рисунок 2.16) убеждаемся в том, что Pcp > PΣ, т. е. неравенство Парсеваля выполняется.

14. Как видно из рисунка 2.13, последовательность прямоугольных импульсов плохо подходит для представления рядом Фурье – она содержит скачки, а сумма любого числа гармонических составляющих с любыми амплитудами всегда будет непрерывной (и более того – бесконечно дифференцируемой во всех точках) функцией. Поэтому поведение ряда Фурье в окрестностях разрывов представляет особый интерес. На временной диаграмме, представленной на рисунке 2.13, хорошо видно, что в окрестности точки разрыва суммирование десяти членов ряда Фурье дает наклонный участок. В самой точке разрыва (в момент времени t = 0) ряд Фурье сходится к полусумме правого и левого пределов:



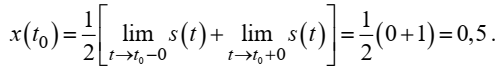
Здесь s(t) – исходный сигнал, sN(t) – сумма усеченного ряда Фурье для него.

На примыкающих к разрыву участках сумма усеченного ряда Фурье дает заметные пульсации. Это явление, присущее рядам Фурье для любых сигналов с разрывами первого рода (скачками), как отмечалось ранее, называется эффектом Гиббса. В ряде работ, например, показано, что амплитуда первого (самого большого) выброса составляет примерно 9 % от величины скачка. Убедимся в этом самостоятельно и определим момент времени tm, с, когда восстановленный по усеченному ряду Фурье сигнал принимает первое после момента времени t = 0 максимальное значение (рисунок 2.18).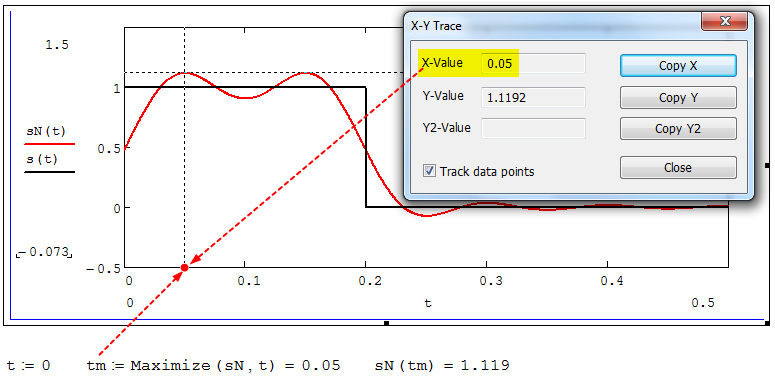


Рисунок 2.18 – Момент времени, когда восстановленный по усеченному ряду Фурье сигнал принимает максимальное значение
Примечание – На рисунке 2.18 реализовано два способа определения

момента времени tm:

- первый способ основан на использовании окна трассировки графика «X-Y Trace»;

- второй способ основан на использовании встроенной в Mathcad функции Maximize(f, var1), которая возвращает значение переменной var1 при котором функция f(var1) принимает максимальное значение. Для того, чтобы исключить неоднозначность определения параметра tm (на рисунке 2.18 у функции

---

имеется несколько максимумов) перед обращением к функции Maximize(f, var1) задано начальное приближение этого параметра t:= 0, т. е. поиск параметра tm производится в начале системы координат при t равном нулю.

15. Вычисляем максимальное значение абсолютной ошибки Δ восстановления сигнала, обусловленное наличием эффекта Гиббса (рисунок 2.19).



Рисунок 2.19 – Максимальное значение абсолютной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса

16. Определяем максимальное значение относительной ошибки восстановления сигнала Δ%, обусловленное наличием эффекта Гиббса, выраженное в процентах (рисунок 2.20).



Рисунок 2.20 – Максимальное значение относительной ошибки восстановления сигнала, обусловленное наличием эффекта Гиббса, выраженное в процентах
Как видно из рисунка 2.20, в рассматриваемом примере, вследствие эффекта Гиббса амплитуда первого (самого большого) выброса составляет примерно 12 % от величины скачка.

17. Исследуем, как повлияет на параметры эффекта Гиббса, изменение количества гармоник спектра сигнала. Увеличим количество гармоник в два и три раза (N = 20 и N = 30). Результат восстановления сигнала и Параметры эффекта Гиббса показаны на рисунках 2.21 и 2.22.


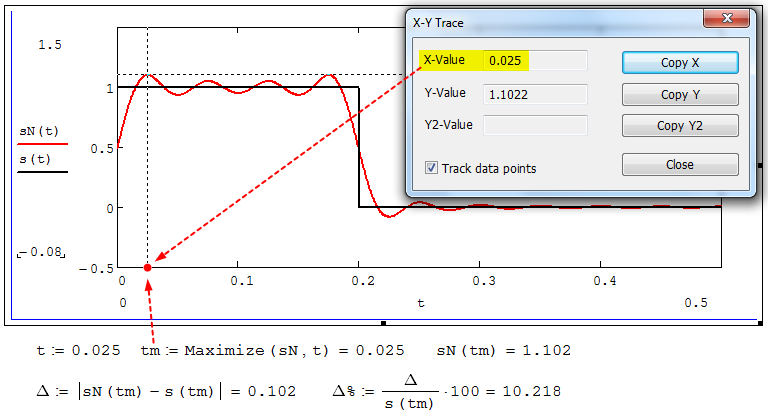
Рисунок 2.21 – Параметры эффекта Гиббса при числе гармоник N = 20



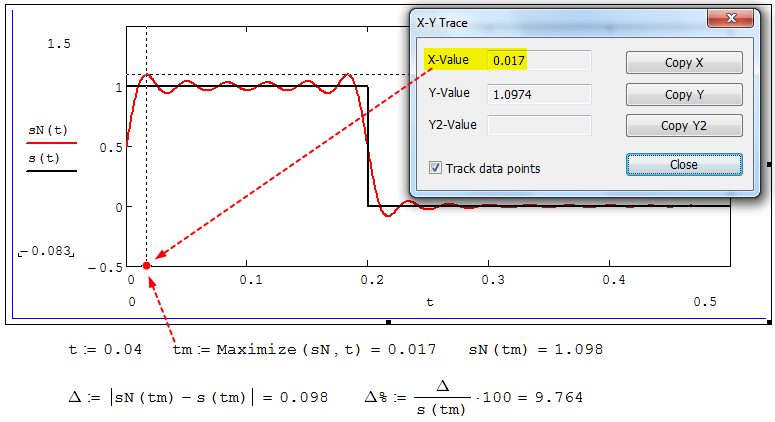
Рисунок 2.22 – Параметры эффекта Гиббса при числе гармоник N = 30
Анализ графика и данных, представленных на рисунках 2.21 и 2.22, свидетельствует о том, что при увеличении количество гармоник в два и три раза (т. е. с 10 до 20 и 30) количество пульсаций восстановленного сигнала тоже удвоилось (утроилось), а амплитуда первого (самого большого) выброса составляет примерно 10 % от величины скачка. Таким образом, исследованный детерминированный, периодический сигнал – периодическая последовательность прямоугольных импульсов (рисунок 2.3) может быть задан функцией s(t) (временной подход) или представлен в виде линейчатого спектра амплитуд и фаз гармоник в базисе Фурье (рисунки 2.11 и 2.12) (спектральный подход).

---

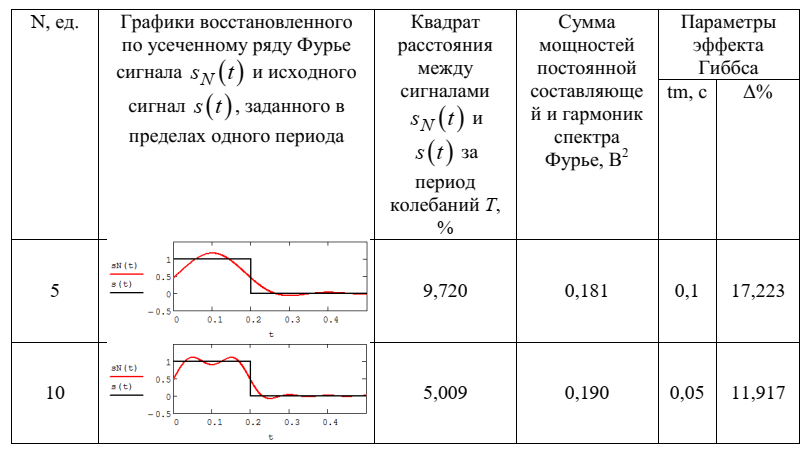
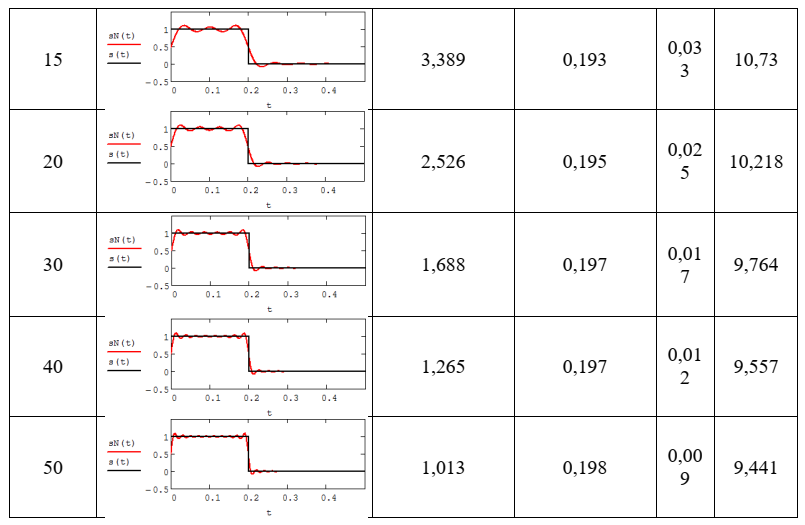
Примечание – В ходе исследования влияния изменение количества гармоник спектра Фурье сигнала на параметры эффекта Гиббса одновременно были исследованы и другие параметры (таблица 2.2).

Из анализа данных, приведенных в таблице 2.2 можно сделать выводы о степени влияния изменение количества гармоник спектра Фурье сигнала на качество восстановления по усеченному ряду Фурье сигнала , выполнение неравенства Парсеваля и параметры эффекта Гиббса сигнала .

Таблица 2.2 – Результаты исследования спектрального анализа

и синтеза периодического сигнала




Порядок выполнения работы

1. Запустить Mathcad.

2. Определить в программе Mathcad для заданного периодического сигнала s(t) в соответствии с вариантом индивидуального задания (таблица 2.3):

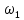- – основную круговую частоту периодического сигнала (частоту первой гармоники), рад/с;

- – коэффициент k-й «косинусной» составляющей спектра Фурье периодического сигнала, В;

- – коэффициент k-й «синусной» составляющей спектра Фурье периодического сигнала, В;

- – постоянную составляющую спектра Фурье периодического сигнала, В;

- – амплитуду k-й гармоники спектра Фурье периодического сигнала, В;

- – начальную фазу k-й гармоники спектра Фурье периодического сигнала, радианы или градусы;

- амплитудную и фазовую спектральные диаграммы периодического сигнала (построить линейчатые спектра);

- восстановленный по усеченному ряду Фурье сигнал являющийся приближенным изображением сигнала s(t);

- расстояние и квадрат расстояния между сигналами

---

Смотрите также файлы

• Установите последовательность, отражающую систематическое положение вида Сосна обыкновенная в классификации растений, начиная с наименьшей группы.docx

• Как Вы считаете, соответствует ли изображенная ниже игрушка требованиям безопасности Аргументируйте свою точку зрения.docx

• Олимпиада по математике 2 класс i тур.docx

• Текст не нужен Текст не нужен.docx

• Протокол от согласовано Общешкольным родительским советом мбоусош7 им П. Н. Степаненко.doc