Определитель полученной матрицы не равен нулю, т.к. b23*a33 - (-1)*0 = 0, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и первое уравнение идентифицируемо.

Проверим второе уравнение системы Y2 = b21Y1 + b23Y3 + a22X2 на выполнение необходимого и достаточного условия идентификации.

В этом уравнении три эндогенные переменные Y1, Y2 и Y3 (H=3). В нем отсутствуют две экзогенные переменные X1 и X3 (D=2). Уравнение идентифицируемо, т.к. D+1=H; (3=3), а значит необходимое условие идентификации выполнено.

, взятых в других уравнениях.

Уравнения, из которых взяты коэффициенты при переменных	Переменные
х1	х3
1	a11	0
3	a31	a33

Определитель полученной матрицы не равен нулю, т.к. a11*a33 - a31*0 = 0, а ранг матрицы равен 2. Значит, достаточное условие выполнено, и второе уравнение идентифицируемо.

Проверим третье уравнение системы Y3 = b32Y2 + a31X1 + a33X3 на выполнение необходимого и достаточного условия идентификации.

В этом уравнении две эндогенные переменные Y2 и Y3 (H=2). В нем отсутствуют эндогенная переменная Y1 и экзогенная переменная X2 (D=2). Уравнение сверхидентифицируемо, т.к. D+1>H; (3>2), а значит необходимое условие идентификации выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных Y1 и X2, взятых в других уравнениях.

Уравнения, из которых взяты коэффициенты при переменных	Переменные
У1	Х2
1	-1	a12
2	b21	a22

---

Задача 1.Зависимость объема продаж (Y) от расходов на рекламу (X) характеризуется по 12 предприятиям концерна следующим образом:



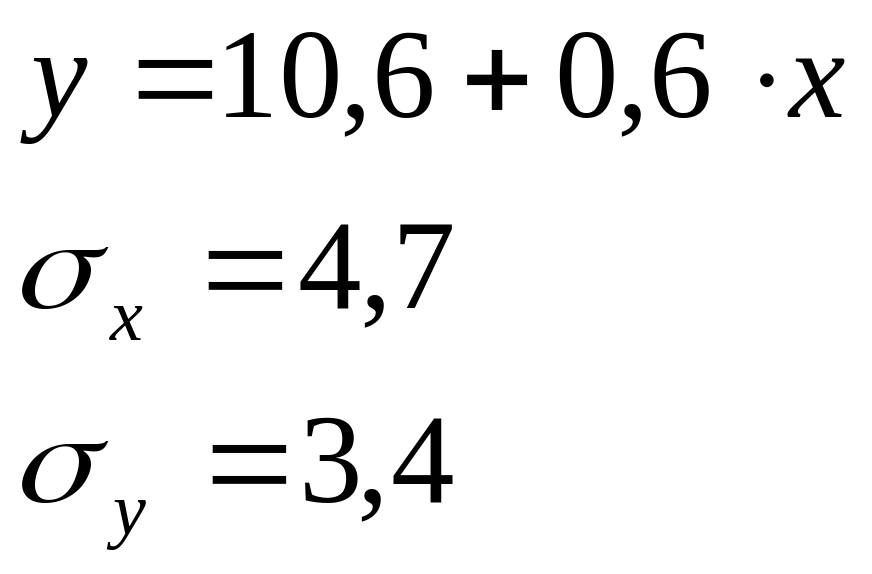
Задание: определите линейный коэффициент парной корреляции, регрессионную сумму квадратов отклонений, постройте таблицу дисперсионного анализа для оценки значимости уравнения в целом, определите F-статистику, t-статистику и доверительный интервал коэффициента регрессии.

Решение:

Для определения коэффициента корреляции применим формулу:



Значение коэффициента корреляции свидетельствует о тесной линейной взаимосвязи между объемом продаж и расходами на рекламу.

Коэффициент детерминации составит:



Определим регрессионную сумму квадратов отклонений:



Составим таблицу дисперсионного анализа и определим F-cтатистику Фишера.

Дисперсионный анализ результатов регрессии

Источники вариации	Число степеней свободы	Сумма квадратов отклонений	Дисперсия на одну степень свободы	F-статистика
				факт.	табл., α=0,05
Регрессионная (объясненная)	1	87,359	87,359	21,949	4,96
Остаточная	10	39,801	3,9801
Общая	11	127,16	11,56

---

Поскольку F_факт >F_табл, то признается статистическая значимость, надежность уравнения регрессии.

Связь между F-статистикой Фишера, t-статистикой Стьюдента для коэффициента регрессии, t-статистикой Стьюдента для коэффициента корреляции выражается равенством:



Значит,   . Табличное значение t-статистики для α=0,05, v=10 составляет 2,2281. Поскольку t_факт>t_табл, то коэффициент регрессии b статистически значимо отличен от нуля.

Экономическая интерпретация параметров линейной модели парной регрессии.



Экономический смысл свободного коэффициента Параметр а, или свободный коэффициент регрессионного уравнения, имеет экономический смысл: он показывает значение результативного признака y, если факторный x = 0.

b — коэффициент регрессии. Показывает, на какую величину в среднем изменится y при увеличении фактора х на 1 единицу.

8.Модели нелинейной регрессии, коэффициент эластичности

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция:



Связано это с тем, что параметр bв ней имеет четкое экономическое истолкование, т. е. он являетсякоэффициентом эластичности. Это значит, что величина коэффициента bпоказывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.

Например, если зависимость спроса от цен характеризуется уравнением вида  , то с увеличением цен на 1 % спрос снижается в среднем на 1,12 %.

В силу того, что коэффициент эластичности для нелинейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний по­казатель эластичностипо формуле:

---

Поскольку коэффициенты эластичности представляют эко­номический интерес, а виды моделей не ограничиваются только степенной функцией, приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии.

Коэффициенты эластичности по разным видам регрессионных моделей.

1.Линейная .

2. Парабола 2 порядка  .

3.  Гипербола  .

4.  Показательная  .

5. Степенная  .

6.  Полулогарифмическая  .

7. Логистическая  .

8. Обратная  .













Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых объясняющих переменных, что необязательно означает улучшение качества регрессионной модели. По этой причине, для устранения этого недостатка, на практике чаще используется скоректированный коэффициент детерминации.

---

В случае линейной зависимости коэффициент детерминации R2 и выборочный коэффициент корреляции rxy связаны соотношением

r2xy = R2.







Модель зависимости объемов продаж компании от расходов на рекламу имеет вид y = -0,31 + 1,5 x _t + 3 x _t-1 + 4,5 x _t-2 + 0,5 x _t-3

Краткосрочный, долгосрочный мультипликатор и средний лаг равны:

—краткосрочный 0,5, долгосрочный 9,2, средний лаг 2,3

+—краткосрочный 1,5, долгосрочный 9,5, средний лаг 0,791

—краткосрочный -0,67, долгосрочный 9,2, средний лаг 0,7

15.Спецификация эмпирического уравнения линейной модели множественной регрессии. Что измеряют коэффициенты регрессии линейной модели множественной регрессии?

Линейная модель множественной регрессии. Эмпирическая форма записи: На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Например, спрос на некоторое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии рассматривается множественная регрессия

Основной целью множественной регрессии является по строение модели с большим числом факторов, а также определение влияния каждого фактора в отдельности и совокупного их воздействия на моделируемый показатель.

. Большая часть анализа является непосредственным расширением парной регрессионной модели, но здесь также появляются и некоторые новые проблемы, из которых следует выделить две. Первая проблема касается исследования влияния конкретной независимой переменной на зависимую переменную, а также разграничения её воздействия и воздействий других независимых переменных. Второй важной проблемой является спецификация модели, которая состоит в том, что необходимо ответить на вопрос, какие факторы следует включить в регрессию (1), а какие – исключить из неё.

---

Смотрите также файлы

• Симптомы дефицита Симптомы избытка.docx

• Тема Историография и источниковедение истории Ставропольского края.docx

• Третья.docx

• Задача Определить, сколько надо вложить при 10% ставке, чтобы через 5 лет получить 100 долл решение.docx

• Самостоятельная работа к теме 1 Заполните чеклист по программе воспитания.docx