Файл: ряд тейлора. Разложение функции в степенной ряд.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.12.2023

Просмотров: 25

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

§ 3. РЯД ТЕЙЛОРА
. Разложение функции в степенной ряд

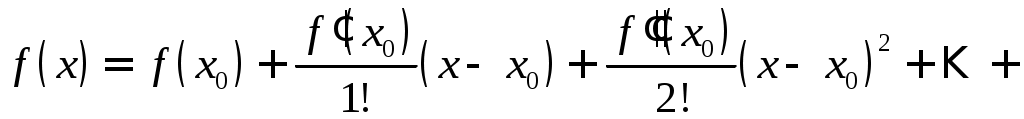
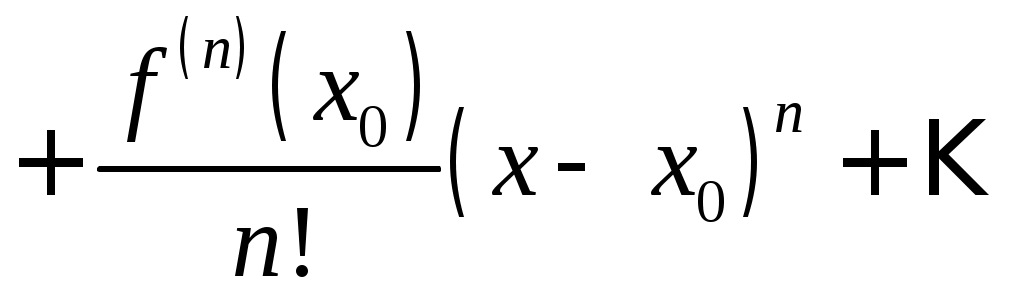Всякая функция, бесконечно дифференцируемая в интервале , т.е. , может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора

, (1)
если в этом интервале выполняется условие

,

где – остаточный член формулы Тейлора (или остаток ряда), .

При получается ряд Маклорена:

.

Если в некотором интервале, содержащем точку , при любом выполняется неравенство , где – положительная постоянная, то и функция разложима в ряд Тейлора.

Для оценки остаточного члена можно пользоваться формулой

где (2)

(форма Лагранжа).

Пример 1. Разложить функцию в ряд по степеням .

Решение. Находим производные данной функции
: , , вообще , если – четное и , если – нечетное. Полагая , получим, , , , , вообще , если

– четное, и , если – нечетное. Отсюда на основании (1) имеем:

(3)

Для определения интервала сходимости ряда (3) применяем признак Даламбера.

Имеем:



при любом . Следовательно, ряд сходится в интервале . Остаточный член в соответствии с формулой (2) имеет вид

, если нечетное , и

, если
четное.

Так как , то

,

,

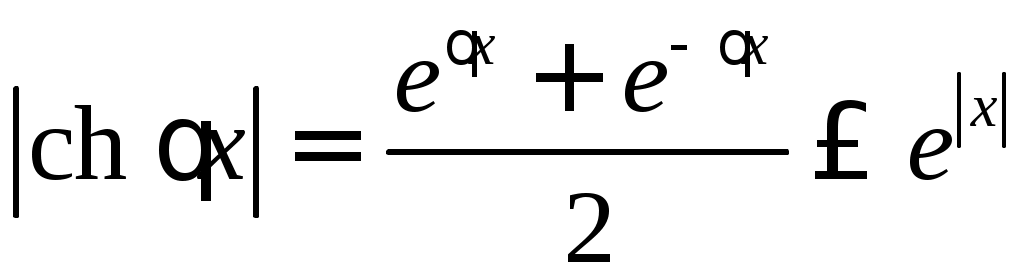и потому . Ряд с общим членом сходится при любом (в этом можно легко убедиться с помощью признака Даламбера), поскольку в соответствии с необходимым признаком сходимости

,

а следовательно, и при любом . Это означает что сумма ряда (3) для любого действительно равна .


. Приемы, применяемые при разложении в степенные

ряды

Пользуясь основными разложениями


  1. ,

  2. ,

  3. ,

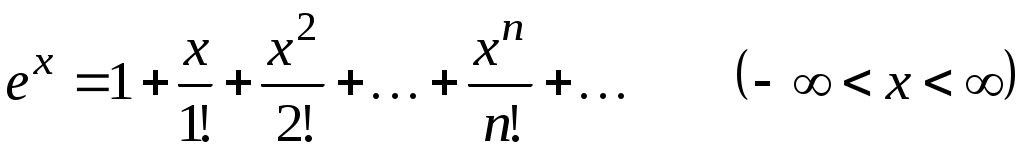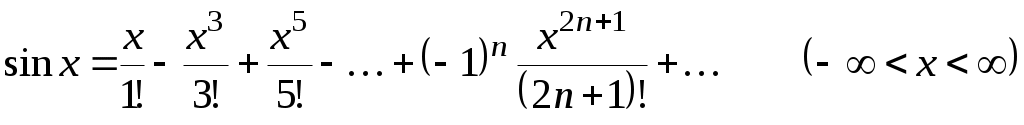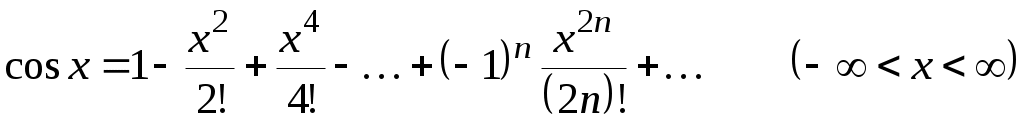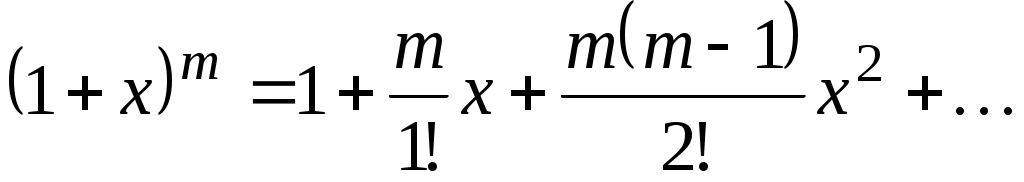
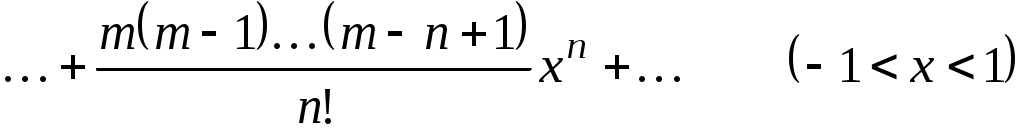  4. ; на границах интервала сходимости это последнее разложение имеет место:

при , если ,

при
, если ,

при , если .

  1. ;

  2. ;

  3. ;

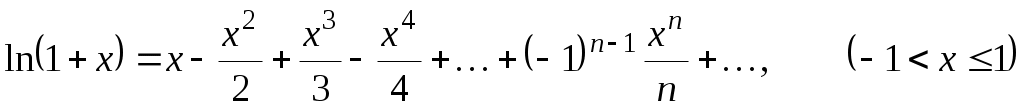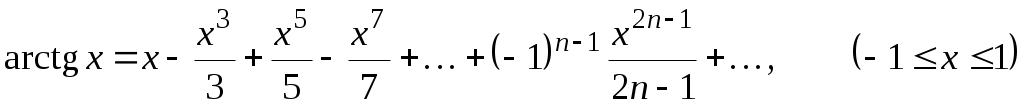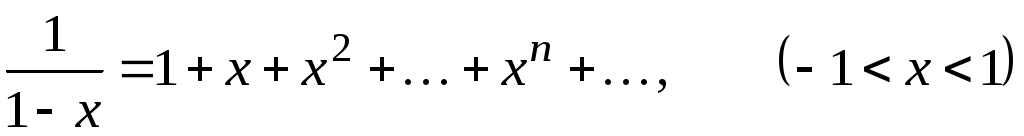можно во многих случаях просто получать разложение данной функции в степенной ряд, причем отпадает необходимость исследования остаточного члена. Иногда при разложении полезно использовать почленное дифференцирование или интегрирование. При разложении в степенные ряды рациональных функций рекомендуется разлагать эти функции на простейшие дроби.

Пример 2. Разложить по целым и положительным степеням функцию .

Решение. Разложив функцию на простейшие дроби, будем иметь:

.

Так как

(4)

и

, (5)

то окончательно

(6)

Геометрические прогрессии (4) и (5) сходятся соответственно при и следовательно, формула (6) справедлива при , т.е. при .

Пример 3. Разложить в ряд по степеням функцию

.

Решение. Продифференцируем функцию раз:

,

,

,

,

,

,

,

.

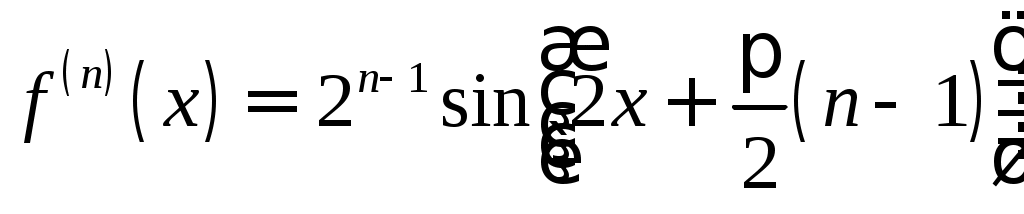Находим значение функций , , ,…, в точке , а значение определяем в точке (см. равенство для определения ). Получаем , , , , , , , …, .

Находим остаточный член:

,

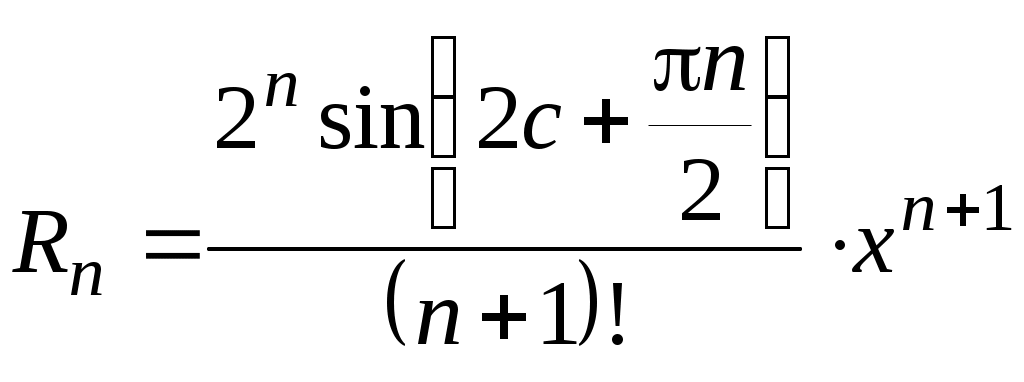т.е.

.

Так как

Смотрите также файлы