ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
при любом  , а
, а 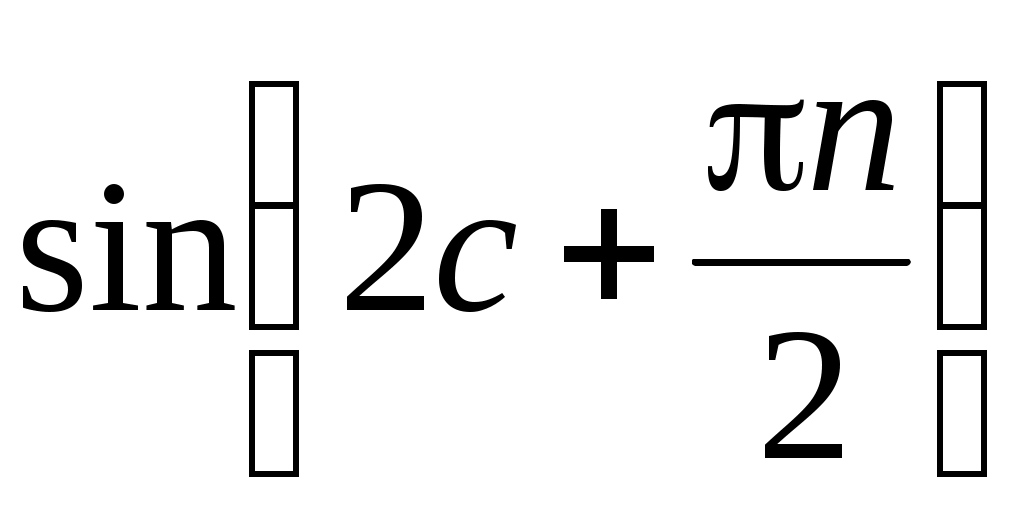 – величина ограниченная, то
– величина ограниченная, то 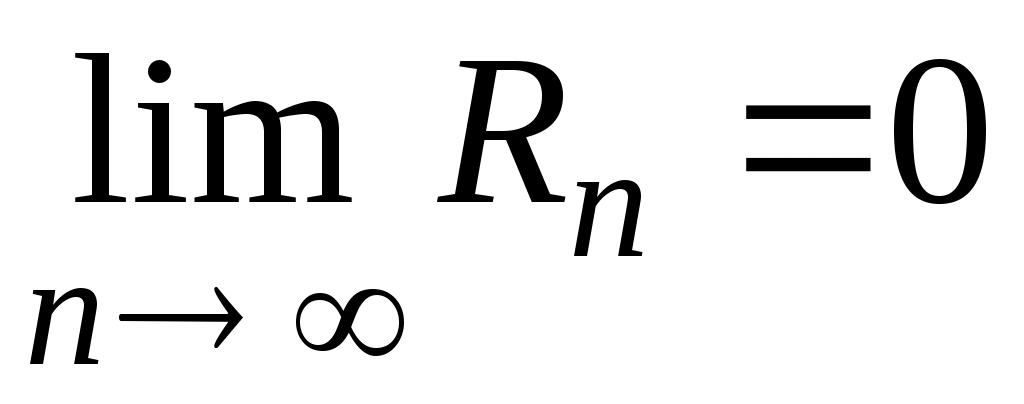 . Следовательно, функцию
. Следовательно, функцию  можно представить в виде суммы ряда Маклорена
можно представить в виде суммы ряда Маклорена
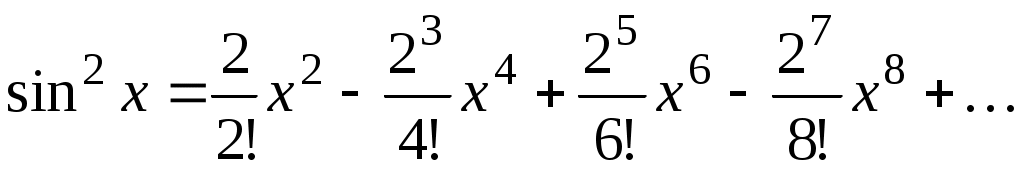 .
.
Задачу можно решить и иначе. В равенстве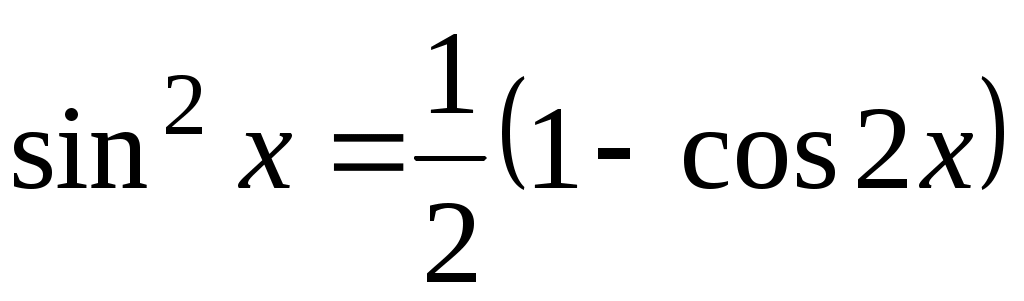 заменим
заменим  его разложением в степенной ряд:
его разложением в степенной ряд:
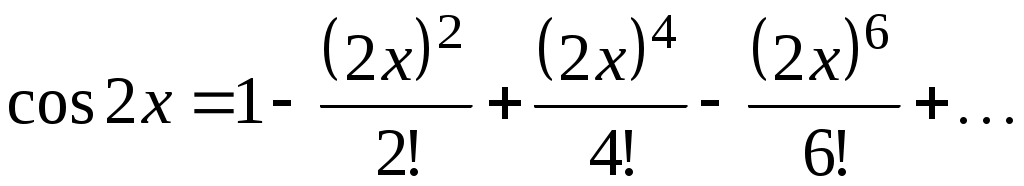 .
.
Выполнив несложные преобразования, получим найденное выше разложение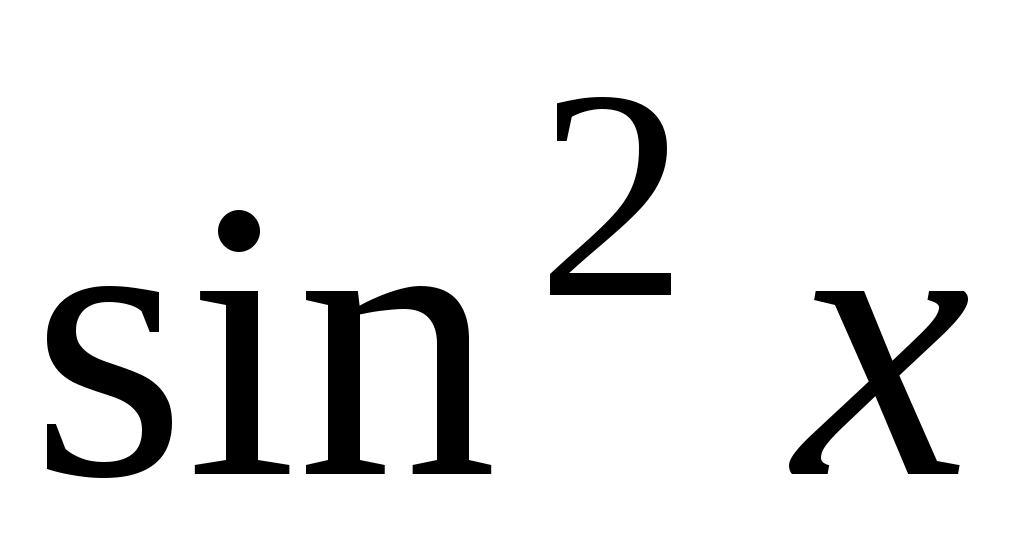 .
.
Пример 4. Разложить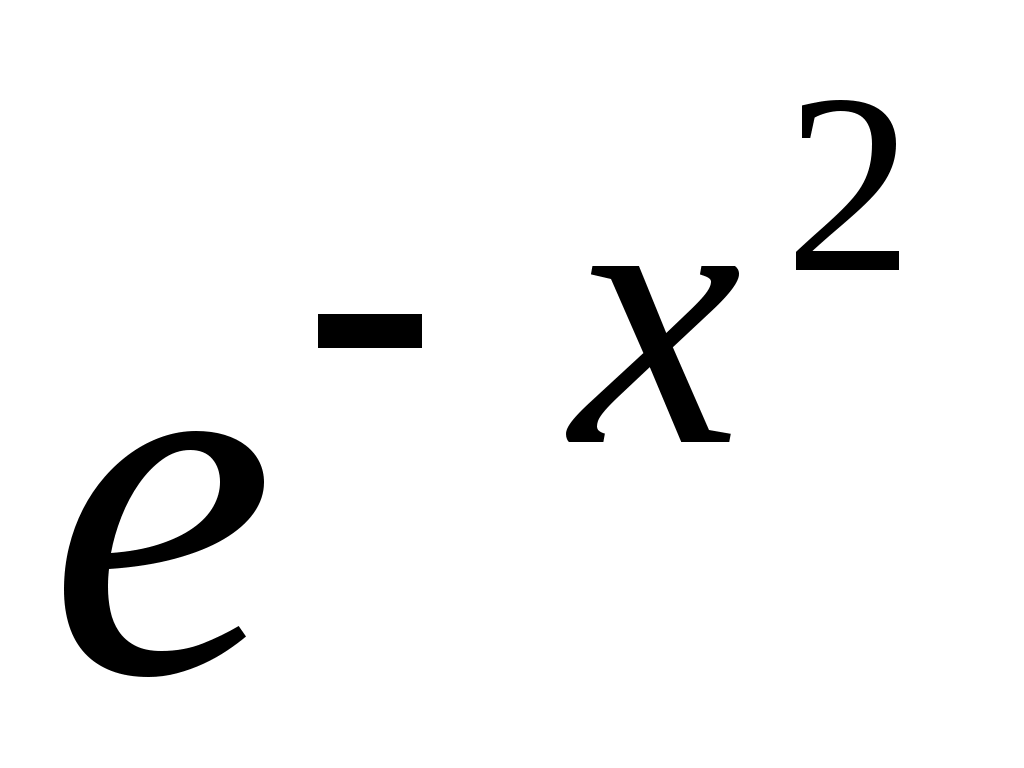 в ряд по степеням
в ряд по степеням  .
.
Решение. В разложении
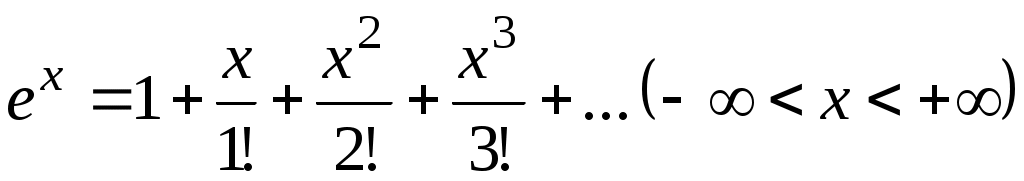
заменим на
на 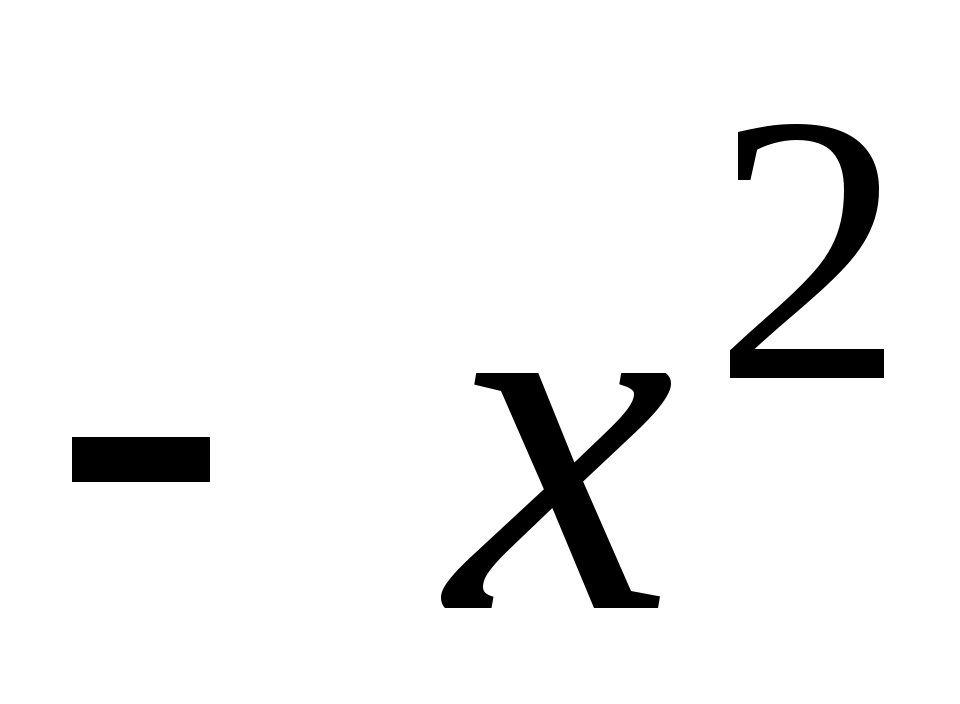 ; получим
; получим
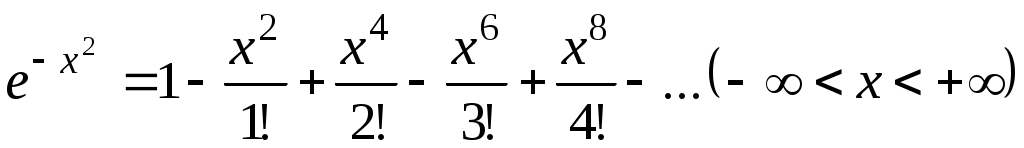 .
.
Пример 5. Разложить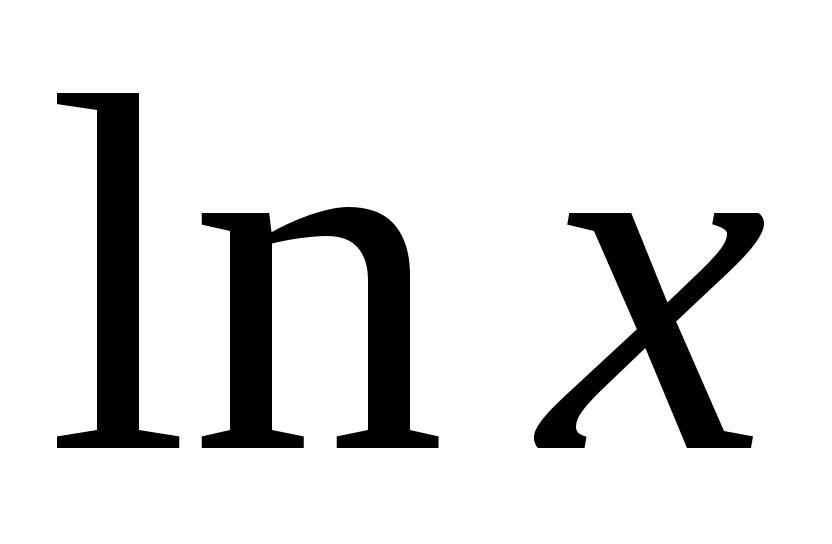 в ряд по степеням
в ряд по степеням 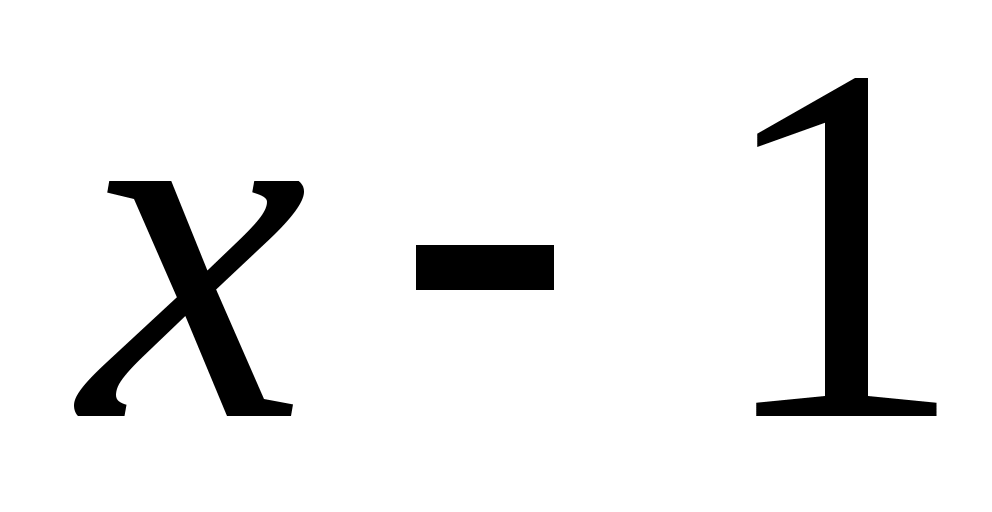 .
.
Решение. В разложении
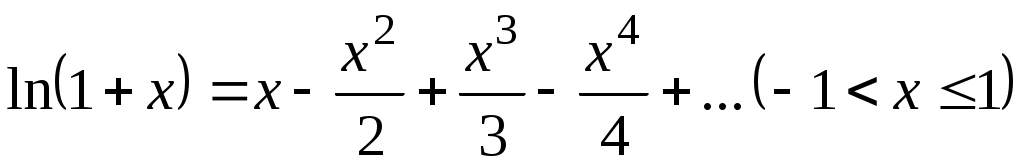
заменим на
на 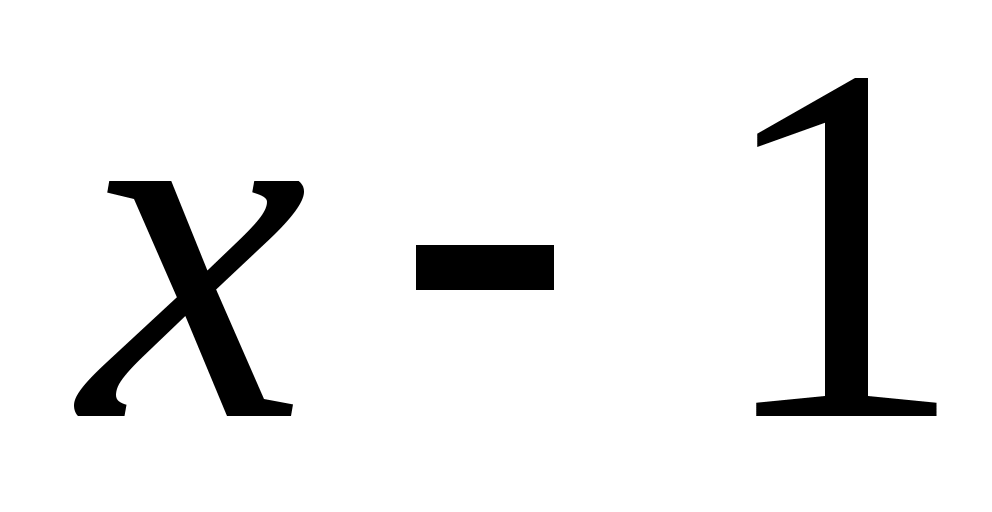 ; получим
; получим
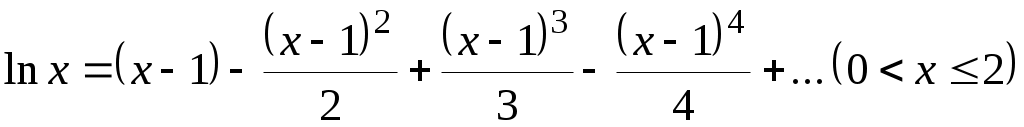 .
.
Пример 6. Разложить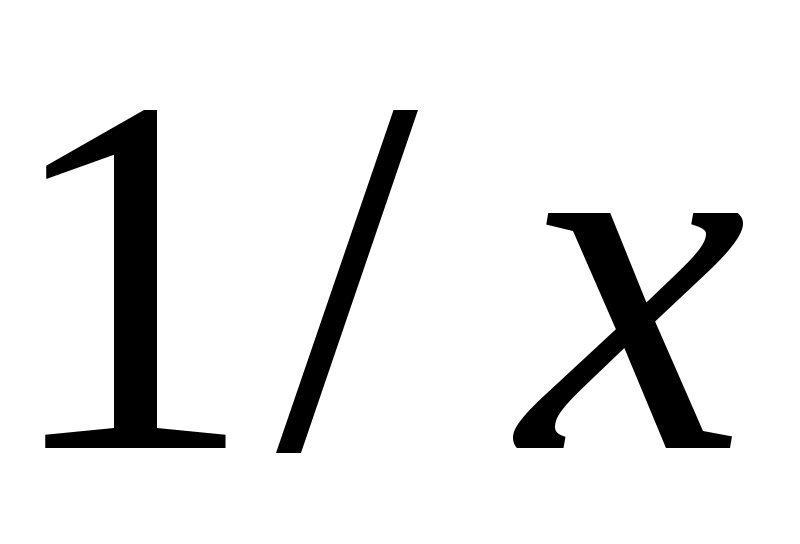 в ряд по степеням
в ряд по степеням 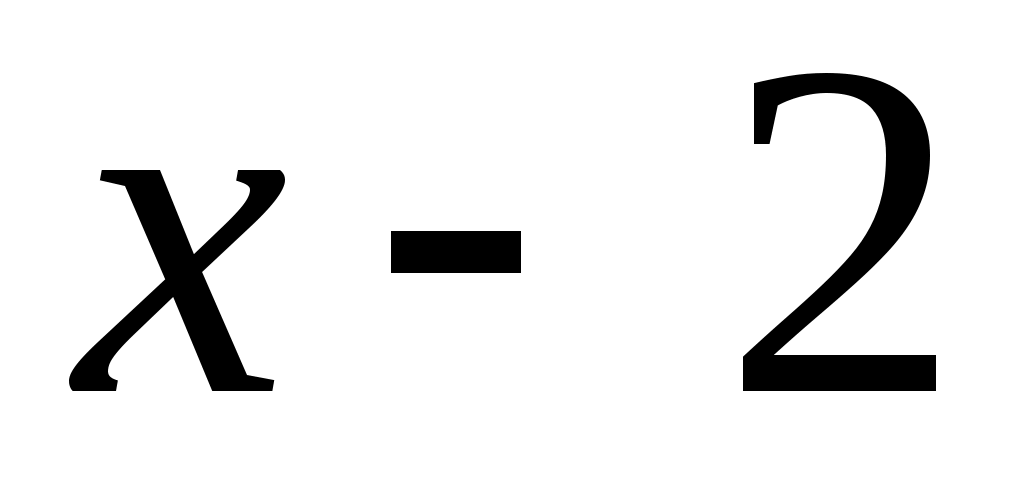
.
Решение. Воспользуемся равенством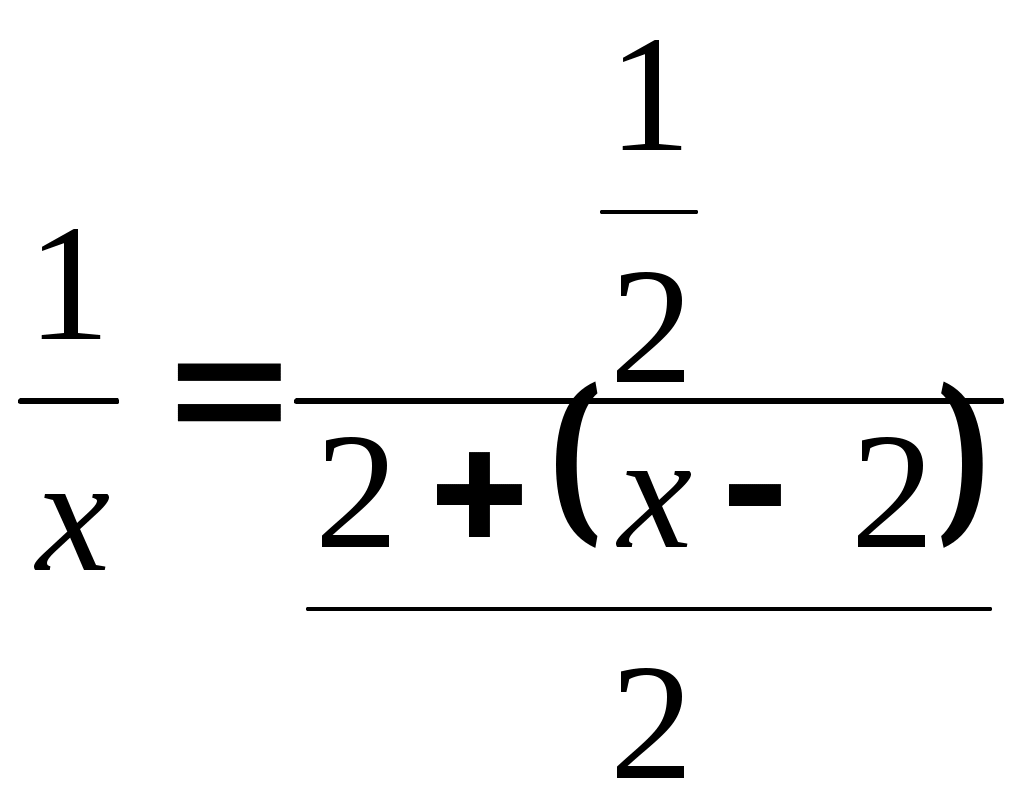 . Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом
. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом 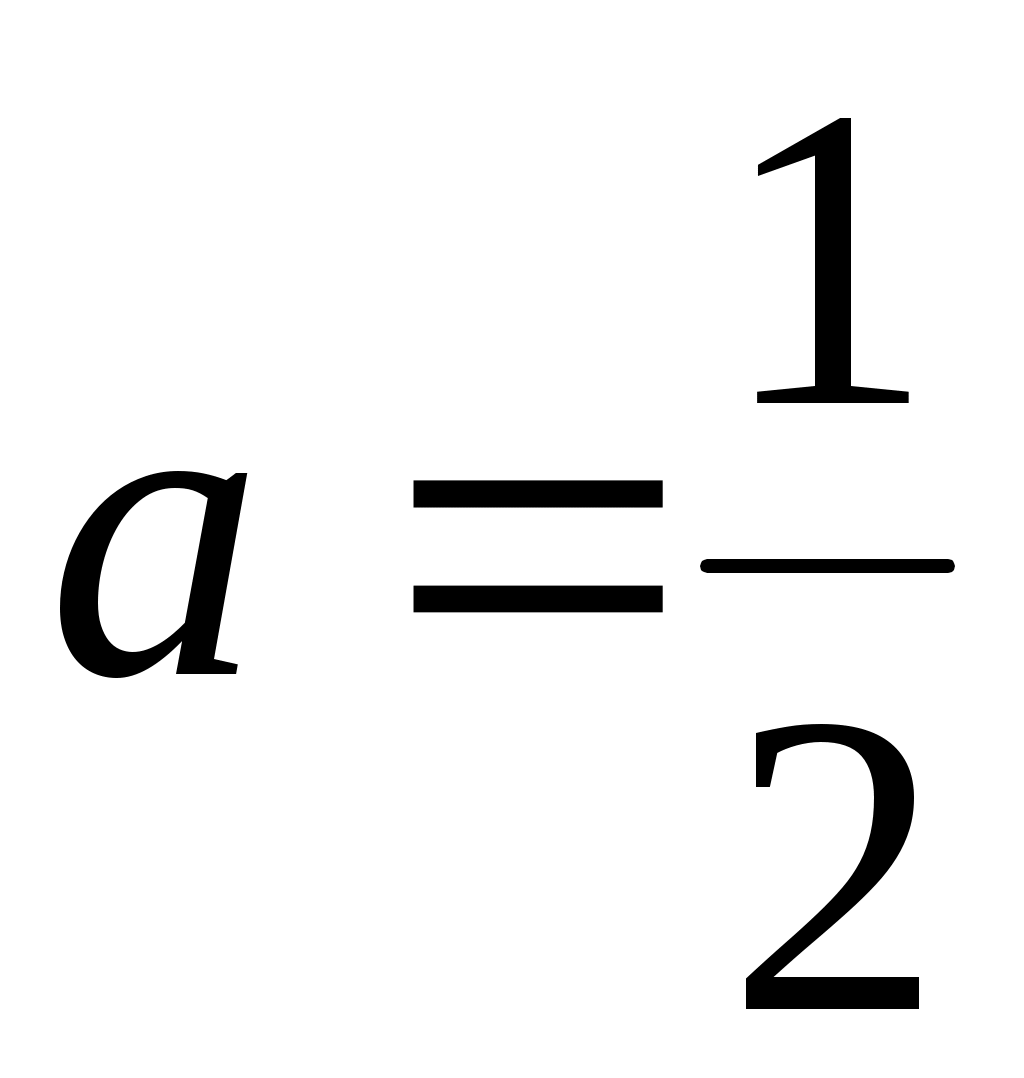 и знаменателем
и знаменателем 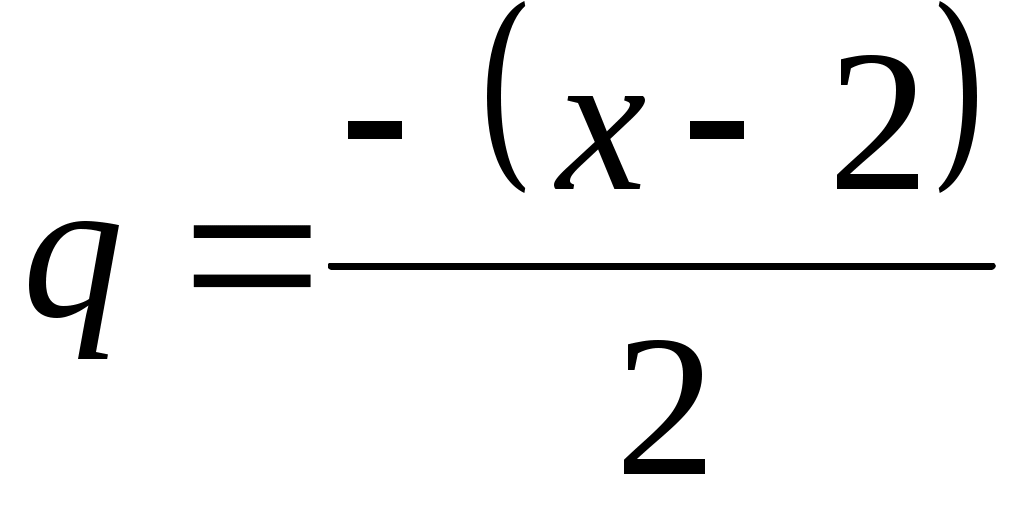 . Отсюда получаем
. Отсюда получаем
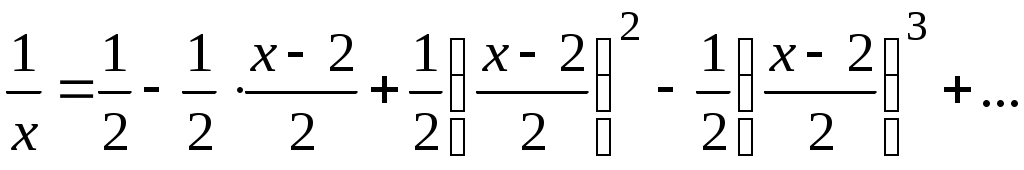 ,
,
т.е.
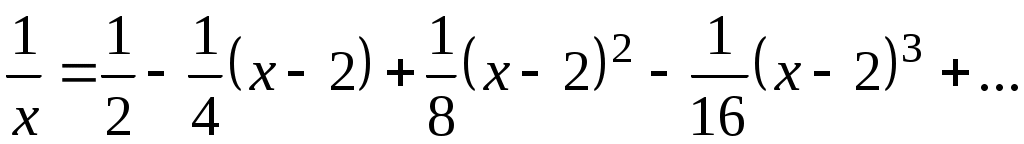 .
.
Так как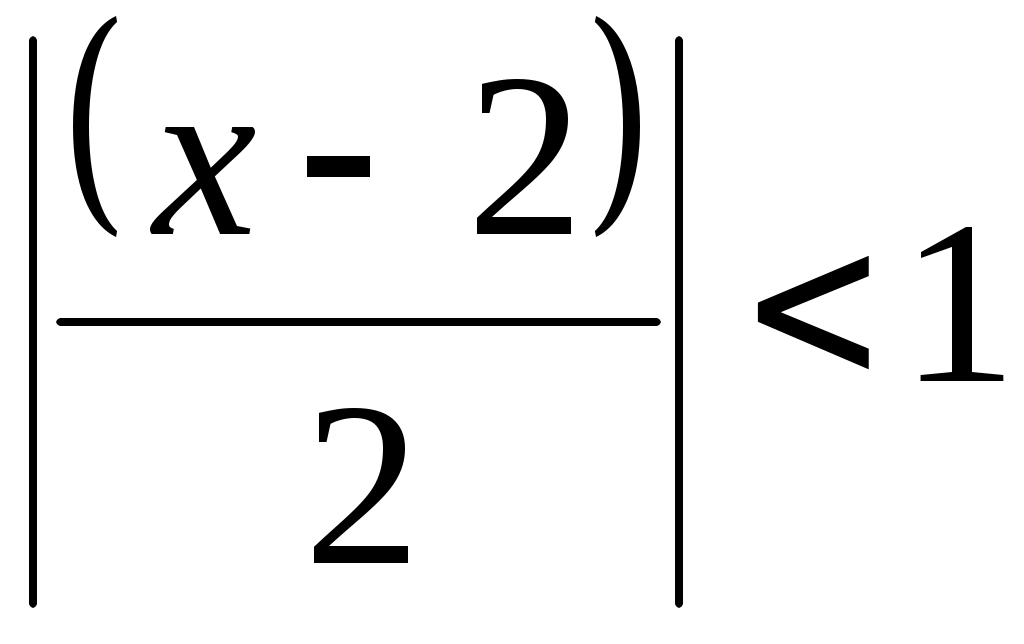 , то
, то 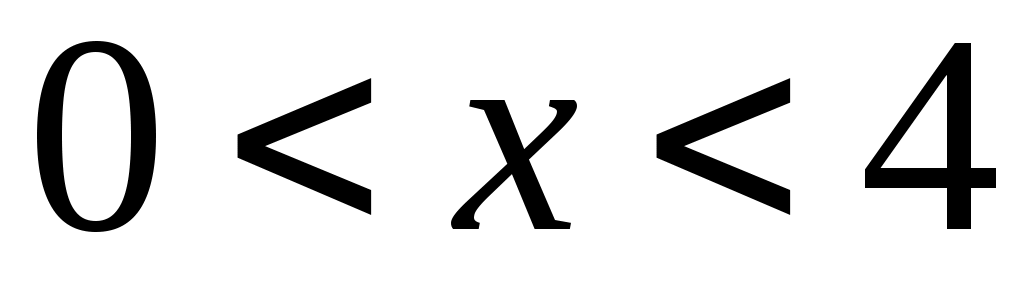 .
.
Пример 7. Разложить в ряд по степеням функцию
функцию 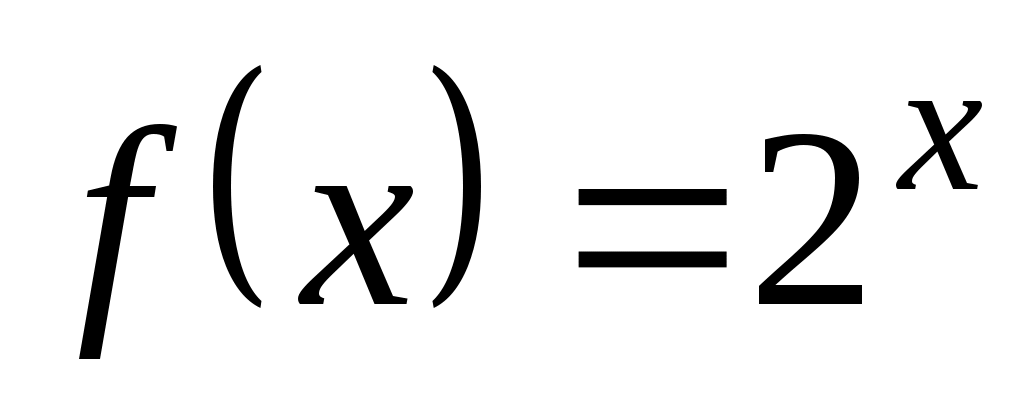 .
.
Решение. Найдем значения функции и ее производных при :
:
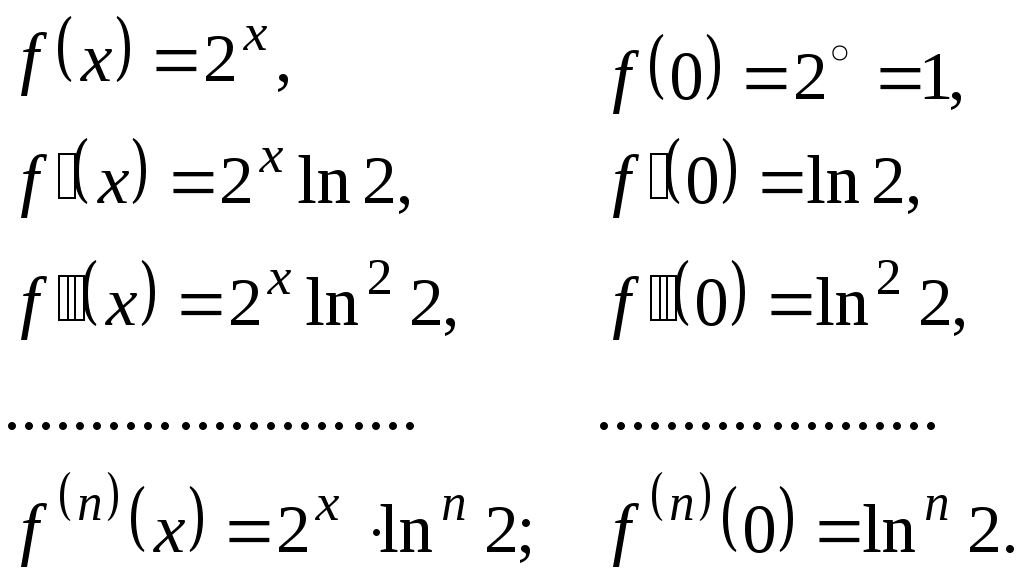
Так как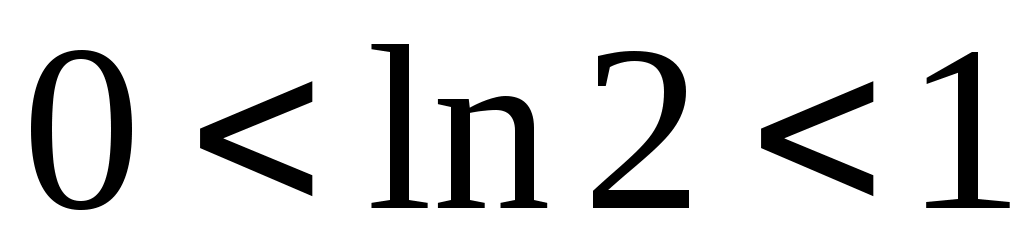 , то при фиксированном
, то при фиксированном  имеет место неравенство
имеет место неравенство 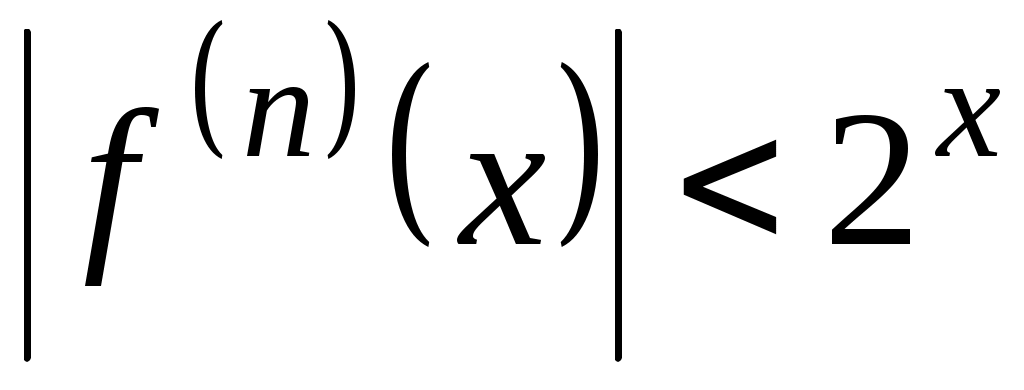 для любого
для любого  . Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
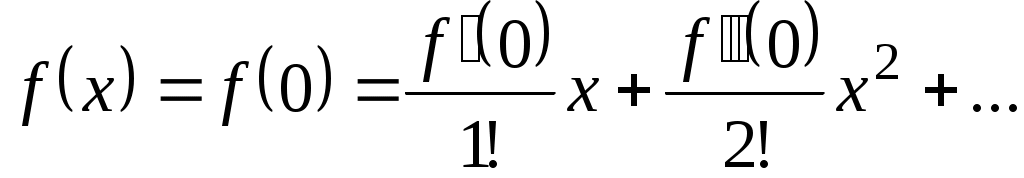 .
.
В данном случае
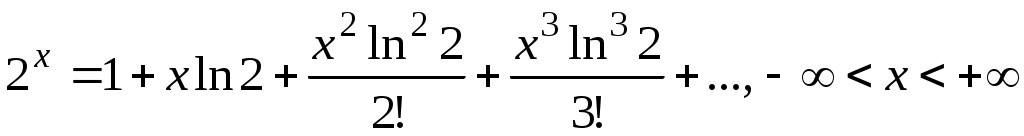 .
.
Это разложение можно получить и иначе: достаточно в разложении
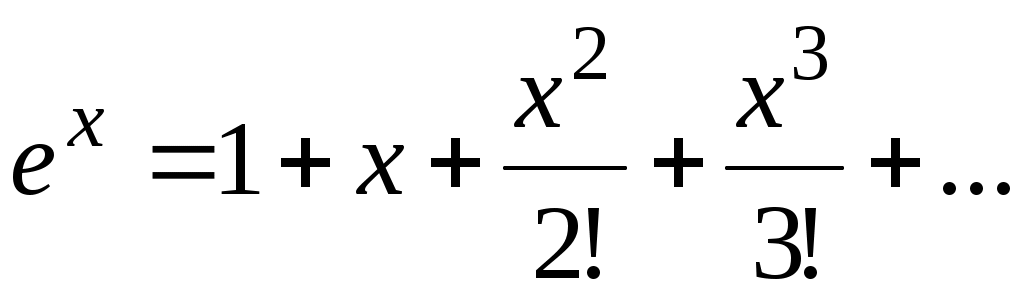
заменить на
на 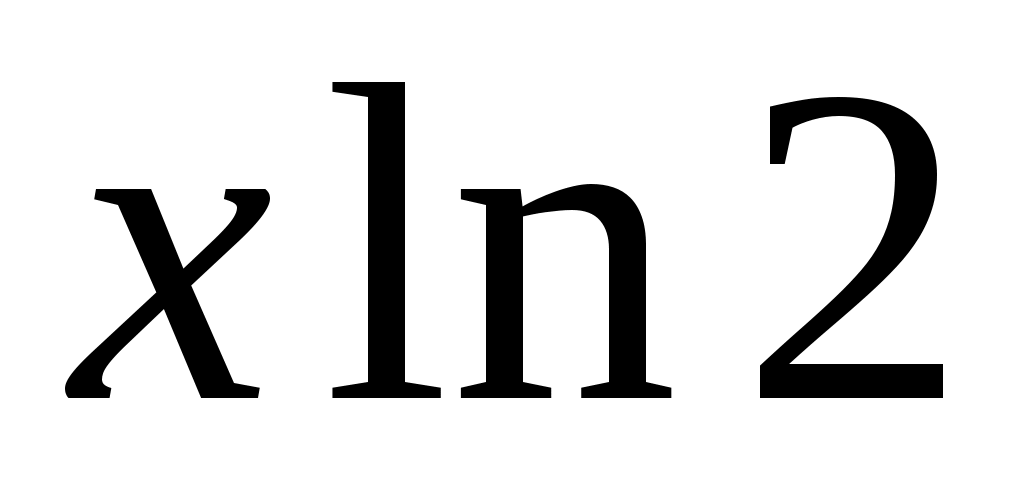 , так как
, так как
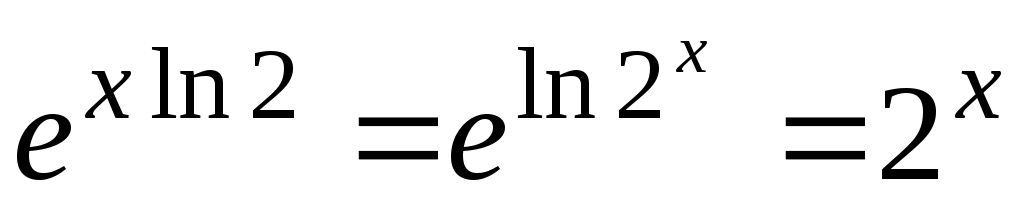 ,
,
тогда
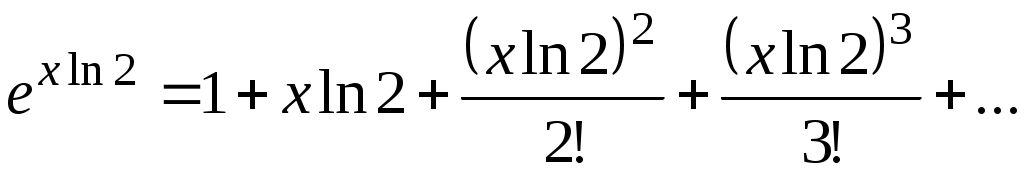
, при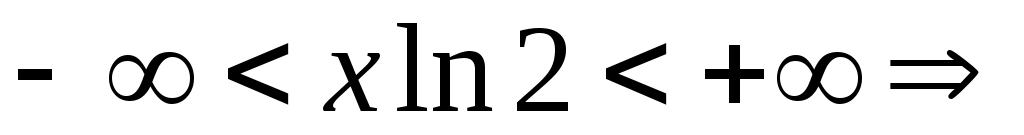
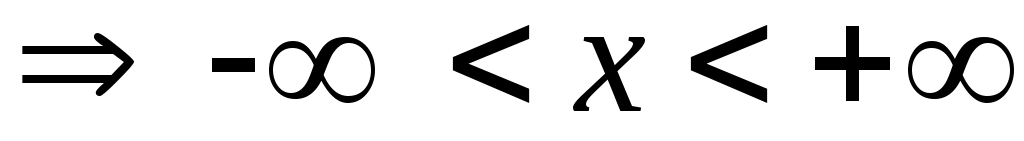 .
.
Задачу можно решить и иначе. В равенстве
Выполнив несложные преобразования, получим найденное выше разложение
Пример 4. Разложить
Решение. В разложении
заменим
Пример 5. Разложить
Решение. В разложении
заменим
Пример 6. Разложить
.
Решение. Воспользуемся равенством
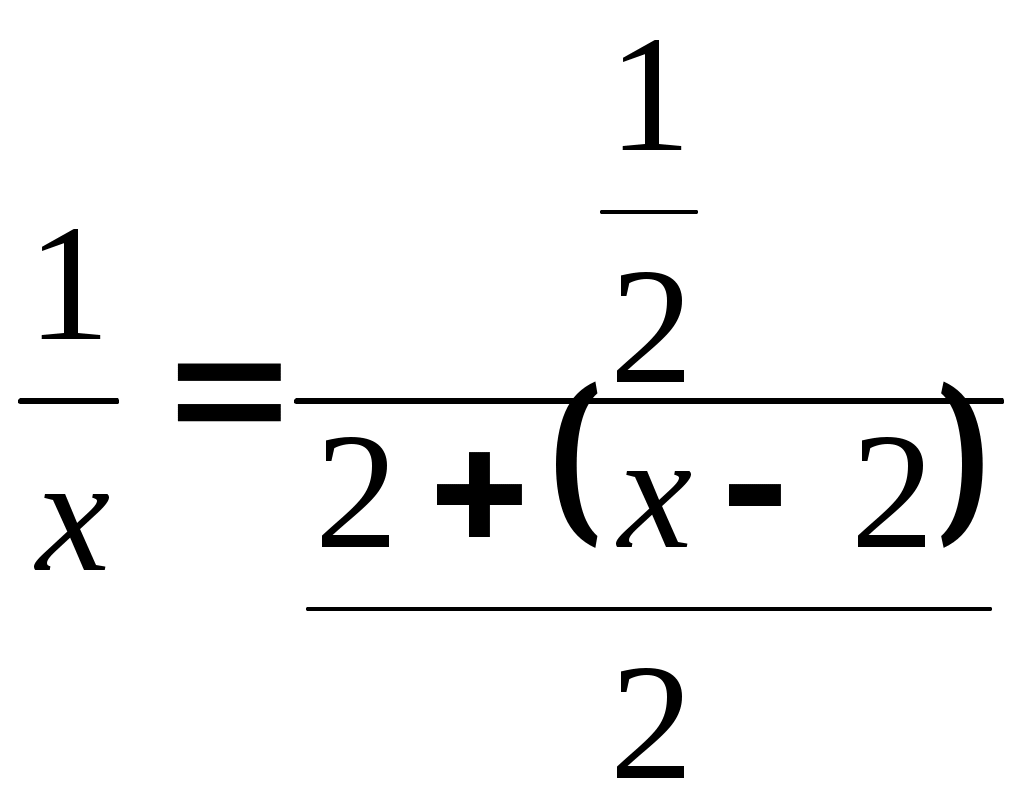 . Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом
. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом т.е.
Так как
Пример 7. Разложить в ряд по степеням
Решение. Найдем значения функции и ее производных при
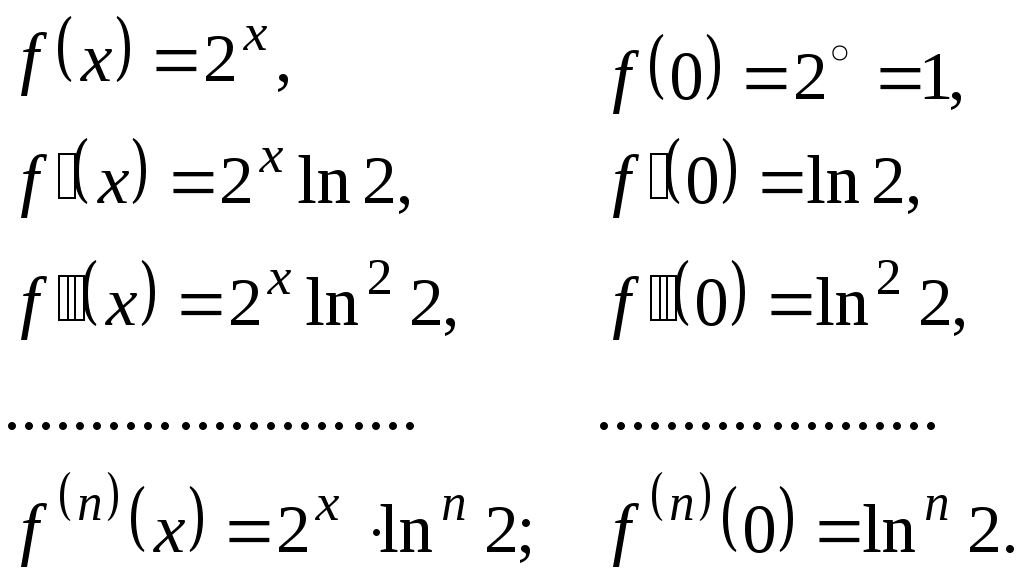
Так как
В данном случае
Это разложение можно получить и иначе: достаточно в разложении
заменить
тогда
, при