Файл: Ытималды Белгілі бір шарттар жиынтыыны жзеге асырылуы нтижесінде пайдаболуы немесе пайда болмауыммкіноиа Кездейсо оиа.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.12.2023

Просмотров: 45

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

БИОСТАТ 100

  1. Қандай-да бір шарттар жиынтығының жүзеге асырылуы нәтижесінде оқиғаныңпайдаболу мүмкіндігінің дәрежесін сипаттайтын сан

++Ықтималдық

  1. Белгілі бір шарттар жиынтығының жүзеге асырылуы нәтижесінде пайдаболуы немесе пайда болмауымүмкіноқиға

  2. ++Кездейсоқ оқиға

  3. Биологиялық нысандарды табиғи және эксперименттік зерттеулердіжоспарлау және олардың нәтижелерін талдау ережелері жөніндегі білімдержүйесі ++Биостатистика

  4. Қоғамдағы құбылыстарды, процестерді сандық және сапалық жағынан тығыз байланыстыра отырып қай жерде және қай уақытта болғанын зерттейтін қоғамдық ғылымның бір саласы

++Статистика

  1. Жиынтықтағы әрбір нысанға тән белгілі бір сапаны сипаттайтын деректер

++Сапалық деректер

  1. Мәндері сан мен өрнектелген айнымалылар

++Сандық деректер

  1. Деректердің бұл түрін өлшеуге немесе мәндері бойынша реттеуге болмайды

++Номинальді немесе категориальді деректер

  1. Деректер қиылыспайтын категорияларға жатады және реттеледі. Бұл түрдегі деректер мен арифметикалық амалдар орындауға болмайды

+ +Реттік деректер

  1. Деректер тек қана белгілі бір анықталған сандық мәндер қабылдайды және арасында аралық мән болмайды

++Дискретті сандық деректер

  1. Деректер берілген диапазондағы кез келген сандық мәнді қабылдайды

++Үздіксіз сандық деректер

  1. Дискретті немесе категориальды деректер үшін++

бағаналы диаграмма;

айналма диаграмма;

сегментелген бағаналы диаграмма;

нүктелік график (диаграмма);

жиіліктер полигоны

Үздіксіздеректерүшін++

гистограмма;

+• «жапырақты сабақша» диаграммасы (stem and leafs);

«мұртты жәшік» диаграммасы (вox and whiskers plot

  1. Қандай да бір сапалық немесе сандық белгілермен сипатталатын нысандар жиыны деп аталады.

++Стаистикалық жиынтық

  1. Жалпы қасиеттерімен біріктірілген барлық зеріттеушілер жиынын....

деп атайды.

++Бас жиынтық

  1. Бас жиынтықтан кездейсотаңдаалынған нысандыр бөлігін деп

атайды.

++Таңдама жиынтық

  1. Таңдама жиынтықты зерттеу негізінде барлық бас жиынтық жөнінде

қорытынды жасауға мүмкіндік беретін статистикалық әдіс

++Таңдама әдіс



  1. Жиілікдегеніміз…..

++берілген интервалда варианталардың неше рет кездесу санын білдіреді

  1. Жинақталған жиілік-

++Берілген белгінің мəнінен кіші байқалған варианталардың байқалған саны

  1. Мода деп...

++Жиі кездесетін кездейсоќ шаманың мәні.

  1. Медианадеп....

++Жиынтықты тең етіп екіге бөлетін белгі мәнін медиана деп атаймыз

  1. Бас жиынтық параметрлері мен қасиеттері туралы анық тұжырым жасау үшін,таңдама болу керек.

++Репрезентативті

  1. Вариациялық қатардеп....

++Варианттарды өсу ретімен жазылған таңдаманы айтады

  1. Таңдаманың статистикалық таралуы деп....

+варианталар мен оларға сәйкес жиіліктердің тізімін айтады және оны кесте арқылы береді:

Бұл түрдегі статистикалық таралуды дискретті статистикалық қатар д.а.
Белгінің мәні x1 x2 x3











Жиілік n1 n2 n3 nk












  1. Кездейсоқ шамалардың кейбір анықталған мәндерді қабылдауы деп

аталады.

++Дискретті

  1. Қалыпты таралу қандай параметрге байланысты:

++Орта мән және дисперсия

  1. Математикалық күтімге қатысты және таралу формасының симметриясын анықтайтын параметр +Гаус қисығы или процентиль

  2. Таралу графигінің шыңының айқындығының көрсеткіші

  3. Егер ассимметрия коэффициенті оң болса,онда...

Оңға қарай қисайған бір немес бірнеше үлкен мәндер
++Сол жаққа созылған ұзын құйрық

  1. Интерваленін анықтау формуласы:

++



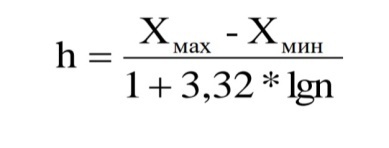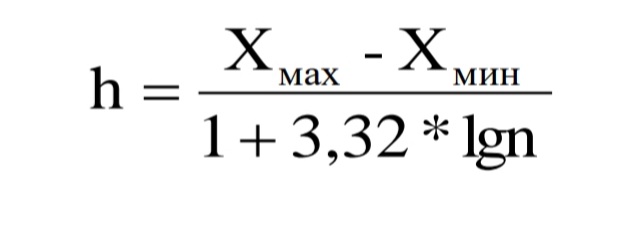
  1. Гаусс заңы бойынша «Х» кездейсоқ шамасының бір қалыпты таралуформуласы: ++

  2. Сызбада берілген кездейсоқ шамалардың үлестірімі:симметиялық



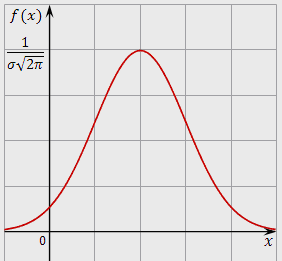
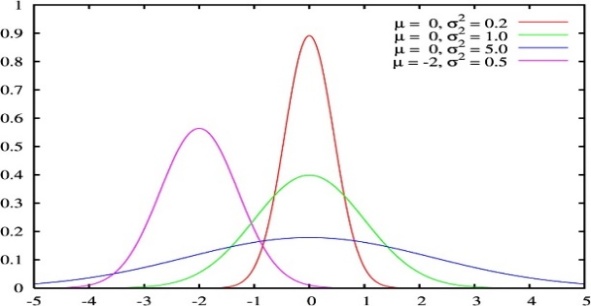
  1. Таралу функциясының тығыздығың бағалау үшін қандай график қолданылады?++Гистограмма

  2. Егер кездейсоқ шама бір қалыпты үлестірілген болса, онда басжинақтыңбарлықмәндерінің...µ±σаралығындажатады.

++барлық мәндердің 68,26% ±σ аралығында жатады орта мәннен ±1 ортаквадраттық ауытқу;

  1. Кездейсоқ шама бір қалыпты үлестірілген болса, онда онда басжинақтың...пайызы µ±2σаралығында жатады.

++барлық мәндердің 95,44% ±2σ аралығында жатады орта мәннен ±2 орта квадраттық ауытқулар

  1. Егер кездейсоқ шама бір қалыпты үлестірілген болса, демек басжинақтыңмәндерінің... µ±3σаралығындажатады.

++барлық мәндердің 99,73% ±3σ аралығында жатады орта мәннен ±3 орта квадраттық ауытқулар.


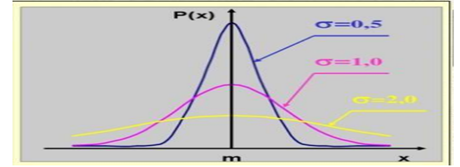
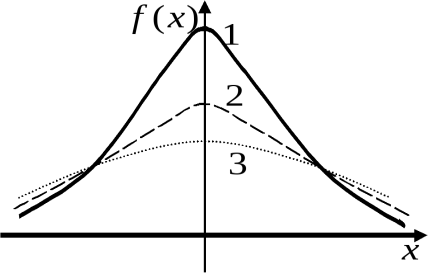  1. Суретте үш қалыпты қисық кескінделген. Қандай қалыпты қисық төмен көрсеткішіне сай келеді +орташа квадраттық ауытқу

1

  1. Параметрлік емес критериялар қолданылады:

++ әртүрлі пішімдегі таралуларға

  1. Манна-Уитни критериясы табылады:

++Тәуелсіз таңдама Статистикалық Параметрлік емес

  1. Вилкоксонныңкритериясытабылады:

++Тәуелді таңдама статистикалық Параметрлік емес

  1. Таңбалар критериясы табылады:++Парамаметрлік емес

  2. Екі тәуелсіз таңдаманы салыстыру үшін қолданатын параметрлік емес белгі:++Стьюденттің жұптаспаған t-критерийі




  1. Бас жиынтықтың таралу түріне негізделмеген және бас жиынтықтың параметрлерін қолданбайтын статистикалық критерийлер:

++Параметрлік емес критерийлер

  1. Параметрлікемес критерийлердің негізіне...жатады.

++Ранжирлеу

  1. Қалыпты таралмаған жұптаса байланысқан таңдамаларды салыстыру

Үшін қолданылатын критерий

++Уилкоксон критерий

  1. Манна-Уитнидың критерийі бойынша Ножорамалдытексеру:

++Екі балама бірдей бас жинтықтармен анықталады

  1. Барлық деректердің белгілі бір ережеге сәйкес ретке келтірілгеннен

Кейінгібақылау жиынтығы қалай аталынады:

++Рангілік жиынтық

  1. Вилкоксонның критерийі бойынша Но жорамалдытексеру:

++Жұптаса байланысқан таңдамалардың бас жиынтықтары бір текті

  1. Егер Вилкоксон әдісіүшінWбақ≤Wсыниболса,онда …

++Н0 жорама жоққа шығарылады

  1. Сәйкестік критерийі–бұл:

++ белгісіз таралу заны туралы болжауды тексеру жорамалы критерийі

  1. Статистикалық жорамалбұл....

++Таралудың түрі жөніндегі болжам

  1. Екіншітектіқателербұл...

++Н1 жоққа шығару, негізінде бұл уақытта ол дұрыс

  1. Біріншітектіқателербұл...

++Н0 жоққа шығару, негізінде бұл уақытта ол дұрыс

  1. Таңдама көрсеткіштердің айтылған болжамды қанағаттыратынын

Анықтауға мүмкіндік беретін процедура

++жорамалды тексеру

  1. 1-текті қателікті жіберу ықтималдығы:

++критерийдің мәнділік деңгейі

  1. 2-тект іқателікті жібермеу ықтималдығы:

++критерийдің қуаттылығы

  1. Бас жиынтықтың таралу түріне негізделмеген, есептеу формуласынатаңдамапараметрлері енбейтінстатистикалықкритерийлер

+ +Параметрлік емес критерийлер

  1. Параметрлік емес критерийлердің негізі болып табылатын

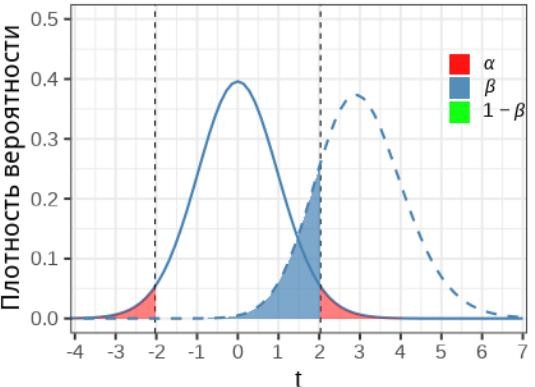++Ранжирлеу

  1. Медицинада қолданылатын сенім ықтималдылығының шамасы

++0,95

  1. Негізгі жорамалды Н0 қабылдау немесе жоққа шығару жөнінде шешімқабылдауға мүмкіндік беретін ереже

++Статистикалық критерий

  1. Таңдама көрсеткіштері негізінде тексеруге болатын таралудың түрі немесе бас жиынтықтың белгісіз параметрлерінің шамалары жөніндегіұйғарым

++Статистикалық жорамал

  1. Жұптасқан көрсеткіштерден тұратын топтың екі өлшемде көрсеткіштерінің орта мәндерін салыстыруда қолданылатын статистикалық талдау әдісі

++Параметрлік еме тәуелді --- Стьюдент т жұптасқан,Вилкоксон критерий

  1. Стьюдент критериясы бойынша нөлдік жорамалды тексеру:

++Екі орта бірғана бас жиынтықта жатады

  1. Стьюденттің критериясы табылады:++Параметрлік

  2. Фишера-Снедекораныңкритериясытабылады:++Параметрлік

  3. Фишер критериясы бойынша нөлдік жорамалды тексеру:

++Бас дисперсиялар бір-біріне тең

  1. Стьюдент критериясы.Егердеtэкспкритболса,онда қандай тұжырым жасауға болады:

++ Нөлдік жорамал қабылданады = екі орта бір бас жиынтықта жатады

  1. Критерия Стьюдента. Егердеtэксп>tкритболса, онда қандай тұжырымжасауға

++Н1 жорамалы кабылданады, екі орта бір бас жиынтықта жатпайды

  1. ФишерF-критерийінесептеуформуласы

б олады: S1>S2

+Нөлдік жорамал жоққа шығарылады = екі орта мəндері тең емес

  1. Екі тәуелді таңдамалардың жұп айырмаларының орта мәндерінің нөлге теңдігі жөніндегі жорамалды тексеру үшін қолданылатын формула:

++ Стьюденттің жұптасқан t критерийі

  1. Дисперсиялар тең тәуелді емес және таңдамалардағы бақылау саны әртүрлі Стьюдент критерийінің еркіндік

дәреже саны

++n1+n2-2

  1. Дисперсиялары тең тәуелді емес және таңдамалардағы бақылаулар саны тең Стьюдент критерийінің еркіндік дәреже саны

++2n-2

  1. Стьюденттің жұптасқан t-критерийі үшін қолданылады

++тәуелді екі топтың орта мәндерін салыстыру

  1. Дәріске қатысқан студенттердің тізімі++дискретті

  2. Науқастыңденесалмағы++Үздіксіз шкала

  3. Науқастыңжынысы:++номинальды(категоиальды)

  4. Аурудыңкезеңдері: ++реттік(ординальды,рангілік)

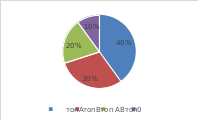
Төмендегі диаграммалардыңқайсысытөмендекөрсетілген? Круговая диограмма?(дөңгелек, Пайчарт)

(қосымшанықараңыз)



  1. Өкпесыйымдылығы
    Төмендегідиаграммалардыңқайсысытөмендекөрсетілген?Точечная диаграмма (нүктелік)++

(қосымшанықараңыз)

  1. Ауру дәрежесі:++ реттік(ординальды,рангілік)

  2. Егер 10 мың студенттерден флюорографиялық тексеру үшін 100 студенткездейсоқ таңдалынып алынған болса, онда алынған жиынтық қалайаталады?

++Тандамалы жиынтық

  1. Қалыпты таралған таңдамада қандай сандық сипаттамалардың теңдігіқарастырылады?

+Таңдама орта,мода және медиана

  1. Келесі кездейсоқ шамалардың модасын тап: 16; 15; 19; 21; 15; 14; 13;17;18.

+15

  1. Бас жиынтықтан нысандарды таңдау кездейсоқ жүргізіледі,яғни

нысандардыңәрқайсысыныңтаңдамағатүсуықтималдылықтарыбірдей;таңдамадағыбақылауларнәтижелерібір-бірінентәуелсіз;барлықнақтышарттарды есепке ала отырып таңдама көлемін дұрыс анықтау; таңдамадағыпропорциялар бас жиынтықтың пропорцияларына сәйкес болу керек. Осышарттарорындалғандатаңдама қалайаталады?

++репрезентативті таңдама

????=????????????????−???????????????? формуласыменесептеугеболады:++Варияциялық ауқымы

+Құлаш

  1. Бес жасарұл балалардыңбой ұзындықтары өлшенді: 101; 103; 95; 97;95; 96; 96; 98; 101; 102; 103; 104;100;98; 98;99таңдаманың көлемiнанықтаңдар:

+16


  1. Берілген таңдамадан ранжирленген вариациялық қатарын құр: 16; 15;26; 18;85;84;35

++15,16,18,26,35,84,85

  1. Егербірқалыптыүлестірілгенкездейсоқшаманынпараметрлеріx=3

және????=3, болса, ондаоныңтығыздығыныңтүрі:

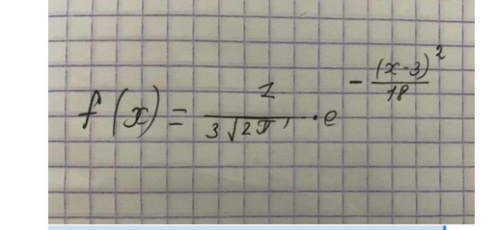
  1. Егербірқалыптыүлестірілгенкездейсоқшаманынтығыздығыныңтүрі

f (x)  122

(x3)2


e
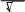 8

,болса, онда:sigma=2 .X=3

  1. Жиіліктіңүлестіріліміндеқалыпкеткенсандардытабыңыз.++ 65 и 70

    Аралық
    Орташа аралық
    Жиілік

    30-40
    35
    11

    40-50
    45
    46

    50-60
    55
    ?

    60-70
    ?
    45

    70-80
    75
    16

    80-90
    85
    1

    Всего



    189

  2. Жиіліктер үлестірілімінің кестесін қолдана отырып, 50 жасқа дейінгіадамдардыңқаншаекенінанықтаңыз:++57

    Жасы
    30-40
    40-50
    50-60
    60-70
    70-80
    80-90

    Жиілік
    11
    46
    70
    45
    16
    1

  3. Жиіліктер үлестірілімінің кестесін қолдана отырып, 60 жастан асқанадамдардыңқаншаекенінанықтаңыз: ++62

    Жасы
    30-40
    40-50
    50-60
    60-70
    70-80
    80-90

    Жиілік
    11
    46
    70
    45
    16
    1

  4. Егер бірқалыпты үлестірілген кездейсоқ шаманын параметрлеріx =3және????=2, болса, ондаоныңтығыздығыныңтүрі: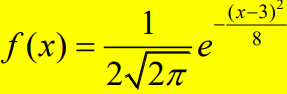

  5. Бірқалыптыүлестірілгенкездейсоқшаманынтығыздығы,

Смотрите также файлы