Отдел образования администрации Центрального района

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 4

Секция: математика


ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

по теме
АРИФМЕТИКИ ФИГУР

Кокорева Валерия Вадимовна, 10^в класс,

МОУ СОШ №4 Центрального района.

224-29-23

Руководитель: Тропина Наталья Валерьяновна,

кандидат педагогических наук,

доцент кафедры математического анализа НГПУ.

(Работа выполнена в МОУ СОШ №4)


Введение
В повседневной жизни мы очень часто используем арифметику чисел, составляющую основу математики. Данная работа содержит результаты исследований за два года; в ней рассмотрены различные варианты выполнения арифметических операций над точками и фигурами. Свойства фигур в этих арифметиках рассмотрены по одним и тем же параметрам для удобства их сравнительного анализа.

В первой части представлена арифметика трех лучей. Как видно из названия, универсумом является пространство, составленное из трех лучей.

Во второй части рассмотрена мультипликативная арифметика, в которой под произведением точек А и В подразумевается отрезок АВ.

Все теоремы и свойства, рассмотренные в работе, доказаны самостоятельно.

Содержание



1. Арифметика трех лучей

1. 
   Основы арифметики
   

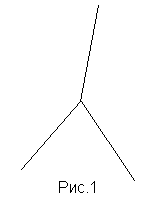
В прошлом году я рассматривала так называемую мультипликативную арифметику, где произведением точек являлся соединяющий их отрезок. Универсумом в ней являлась плоскость, и я рассматривала только фигуры, являющиеся ее подмножествами. В арифметике трех лучей универсумом являются три луча, выходящие из одной точки (рис.1). Все последующие операции будут рассматриваться только для фигур, являющихся подмножествами этого трехлучевого пространства.

---

2. 
   Понятие умножения. Свойства умножения точек
   

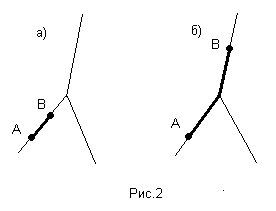
Под произведением двух точек А и В будем подразумевать отрезок, соединяющий эти точки (рис.2). Отрезок с концами А и В в трехлучевой арифметике – это кратчайшая ломаная, соединяющая точки А и В.

Существуют два принципиально различных варианта расположения двух точек в трехлучевом пространстве, но произведение этих точек для любых точек А и В определяется единственным образом. На рисунке 2а рассмотрен вариант , при котором точки А и В расположены на одном луче, а на рисунке 2б – на разных.



Такое умножение точек обладает следующими свойствами:

А) Коммуникативность

АВ=ВА

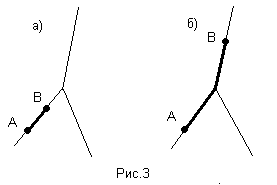
Свойство доказано графически, перебором всех принципиально различных вариантов расположения точек (рис.3) На рисунке 3а рассмотрен случай, когда обе точки лежат на одном луче, а на рисунке 3б – когда они лежат на разных лучах. Таким образом, рассмотрены все принципиально различные варианты расположения точек А и В (случаи аналогичных ситуаций, когда точки А и В просто лежат на других лучах, можно не рассматривать, т.к. они абсолютно идентичны при повороте универсума).



При графическом доказательстве дальнейших свойств метод и ход доказательства аналогичен, поэтому подробное описание каждого случая опускается.

Б) Ассоциативность

(АВ)С=А(ВС)

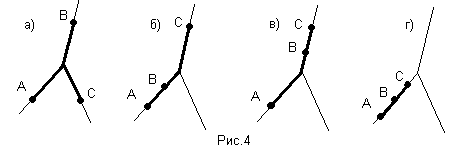
Доказательством этого свойства является перебор всех принципиально различных вариантов расположений точек А, В и С, с проверкой выполнения данного свойства (рис.4), как и в случае с коммутативностью.



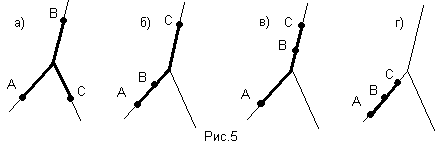
В) Дистрибутивность относительно сложения

Под суммой двух точек будем подразумевать их объединение.

А(В+С)=АВ+АС. Доказательство графическое (рис.5).



Г) Идемпотентность

АА=А. Произведением точки А самой на себя является кратчайшая ломаная, соединяющая точку А с самой точкой А. Этой кратчайшей ломаной является сама точка А.

3. Умножение фигур

Под произведением фигур

---

будем подразумевать объединение произведений всех точек фигуры на каждую точку фигуры .

Такое умножение обладает следующими свойствами:

А) Коммуникативность



Теорема (о коммутативности умножения фигур)

Произведение двух фигур коммутативно.

Доказательство

По определению умножения фигур мы должны умножить все точки фигуры на каждую точку фигуры . Таким образом, мы можем представить произведение как объединение произведений точек фигур и . Умножение точек коммутативно, поэтому можно во всех таких произведениях можно переставить точки исходных фигур.

Теорема доказана.

Для доказательства дальнейших свойств нам потребуется определить понятия ограниченных и неограниченных фигур.

Ограниченная на луче фигура в трехлучевой арифметике – это такая фигура, для которой можно определить расстояния от центра универсума до наиболее удаленной точки на этом луче.

Неограниченная на луче фигура в трехлучевой арифметике – это фигура, для которой нельзя определить расстояние от центра универсума до точки, наиболее удаленной от него на этом луче.

Фигура может быть ограниченной на одном луче и неограниченной на другом.

Б) Ассоциативность

Теорема (об ассоциативности умножения фигур)

Произведение трех фигур ассоциативно.

Доказательство

Пусть , и - это исходные фигуры. Требуется доказать, что

---

. Разобьем доказательство на три случая – когда точки объединения фигур лежат на одном, двух и трех луча универсума, а каждый из этих случаев – на подслучаи, когда это объединение является ограниченной и неограниченной фигурой на различных лучах.

1 случай: объединение лежит на одном луче.

1 подслучай: объединение ограничено на этом луче. Определим наиболее и наименее удаленные от центра универсума точки. Независимо от порядка умножения результатом будет являться отрезок, соединяющий эти точки.

2 подслучай: объединение неограниченно на этом луче. Определим наименее удаленную от центра универсума точку. Независимо от порядка умножения результатом будет являться луч с началом в наименее удаленной от центра универсума точке объединения, продолжение которого проходит через воображаемую бесконечно удаленную от центра универсума точку.

2 случай: объединение лежит на двух лучах.

1 подслучай: объединение ограниченно на обоих лучах. Определим наиболее удаленные от центра универсума точки объединения. Независимо от порядка умножения результатом будет отрезок, соединяющий эти точки.

2 подслучай: объединение ограниченно на одном луче и неограниченно на другом. Определим наиболее удаленную от центра универсума точку объединения на луче, на котором объединение ограниченно. Независимо от порядка умножения результатом будет объединение отрезка, соединяющего центр универсума и наиболее удаленную точку, и луча, на котором объединение фигур неограниченно.

3 подслучай: объединение неограниченно на обоих лучах. Независимо от порядка умножения результатом будет объединение лучей, на которых объединение фигур неограниченно.

3 случай: объединение фигур лежит на трех лучах.

1 подслучай: объединение ограниченно на всех трех лучах. Определим наиболее удаленные от центра универсума точки на каждом из лучей. Независимо от порядка умножения результатом будет объединение отрезков, соединяющих центр универсума с наиболее удаленными точками на каждом луче.

2 подслучай: объединение ограниченно на двух лучах и неограниченно на третьем. Определим наиболее удаленные от центра универсума точки на лучах, на которых объединение фигур ограниченно. Независимо от порядка умножения результатом будет объединение отрезка, соединяющего эти точки, и луча, на котором юбъединение исходных фигур неограниченно.

---

3 подслучай: объединение ограниченно на одном луче и неограниченно на двух других. Определим наиболее удаленную от центра универсума точку на луче, на котором объединение фигур ограниченно. Независимо от порядка умножения результатом будет объединение отрезка, соединяющего эту точку с центром универсума. и лучей, на которых объединение фигур неограниченно.

4 подслучай: объединение неограниченно на всех трех лучах. Независимо от порядка умножения результатом будет весь универсум.

Теорема доказана

Соответственно, доказано и свойство.

В) Дистрибутивность относительно сложения

. Это очевидно, т.к для того, чтобы умножить одну фигуру на другую, нужно перемножить все их точки, а в роли второй фигуры сейчас выступает объединение фигур.

Более того, можно заметить, что действует следующее свойство:

Г) Псевдокоммутативность



Разобьем доказательство на три случая – когда точки объединения фигур лежат на одном, двух и трех луча универсума, а каждый из этих случаев – на подслучаи, когда это объединение является ограниченной и неограниченной фигурой на различных лучах.

1 случай: объединение лежит на одном луче.

1 подслучай: объединение ограничено на этом луче. Определим наиболее и наименее удаленные от центра универсума точки. Независимо от способа умножения результатом будет являться отрезок, соединяющий эти точки.

2 подслучай: объединение неограниченно на этом луче. Определим наименее удаленную от центра универсума точку. Независимо от способа умножения результатом будет являться луч с началом в наименее удаленной от центра универсума точке объединения, продолжение которого проходит через воображаемую бесконечно удаленную от центра универсума точку.

2 случай: объединение лежит на двух лучах.

1 подслучай: объединение ограниченно на обоих лучах. Определим наиболее удаленные от центра универсума точки объединения. Независимо от способа умножения результатом будет отрезок, соединяющий эти точки.

2 подслучай: объединение ограниченно на одном луче и неограниченно на другом. Определим наиболее удаленную от центра универсума точку объединения на луче, на котором объединение ограниченно. Независимо от способа умножения результатом будет объединение отрезка, соединяющего центр универсума и наиболее удаленную точку, и луча, на котором объединение фигур неограниченно.

---

Смотрите также файлы

• Контрольноизмерительный материал для проведения промежуточной аттестации обучающихся 10 класса по Информатике и икт за 2019 2020 учебный год Спецификация контрольных измерительных материалов Назначение ким.docx

• Задание Философия и ее роль в жизни и обществе i впишите пропущенные термины, слова и имена.docx

• Тема Зоопсихология как научная.docx

• В. Ю. Бабошкин 20 г.docx

• "АлтынЕмель" в наследие юнеско включён.docx