Файл: Исследовательская работа по теме арифметики фигур кокорева Валерия Вадимовна, 10 в класс, моу сош 4 Центрального района. 2242923.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, т.е. любые две точки соединены отрезком внутри произведения. Значит, получили противоречие, следовательно, наше предположение не верно, значит, произведение двух выпуклых фигур – выпукло. Теорема доказана.
В данном пункте приведены примеры умножения различных фигур.
На рисунке 18 показано умножение точки на отрезок.
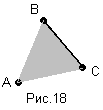
На рисунке 19 – результат умножения квадрата на круг.
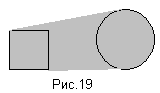
На рисунке 20 вы можете увидеть результат умножения точки на круг на прямоугольник.
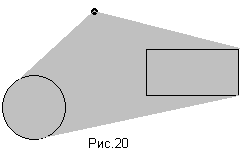
Натуральная степень фигур.
В арифметике и в алгебре особую роль играют те числа, квадрат которых равен им самим. Ясно, что этим свойством обладают лишь два числа: 1 и 0.
В мультипликативной геометрии этим свойством обладают выпуклые фигуры. Фигура – это произвольное множество точек плоскости. Выпуклая оболочка фигуры – это наименьшая степень, при возведении в которую мы получаем выпуклую фигуру.
Теорема (о выпуклой оболочке плоских фигур).Выпуклой оболочкой любой фигуры на плоскости будет ее третья степень.
Доказательство.Пусть точки А и В принадлежат фигуре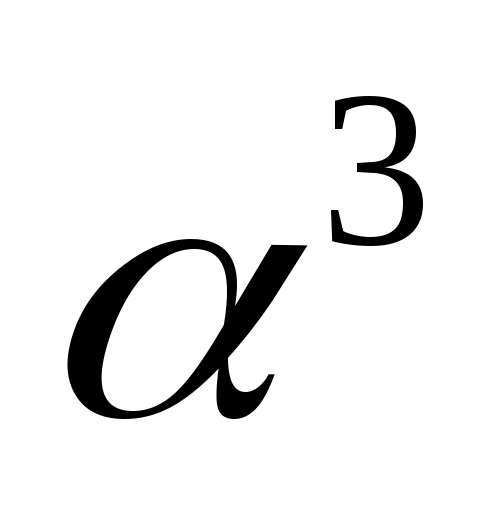
. Для доказательства теоремы нам достаточно доказать, что отрезок АВ будет подмножеством этой фигуры. Пусть точки А и В принадлежат отрезку PN, причем Р принадлежит фигуре 
, а точка N – фигуре 
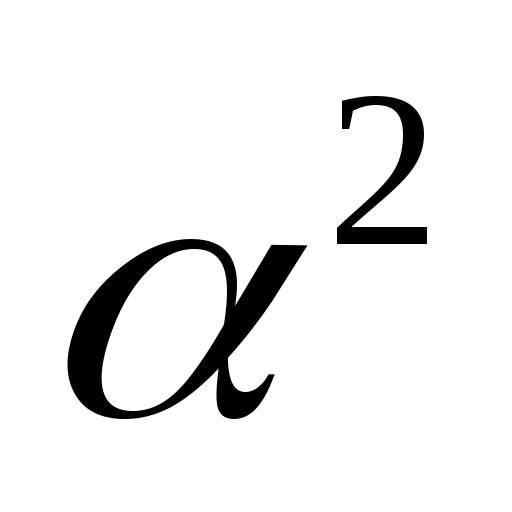. Т.к. произведение любой фигуры саму на себя содержит эту фигуру, то точки Р и N принадлежат фигуре 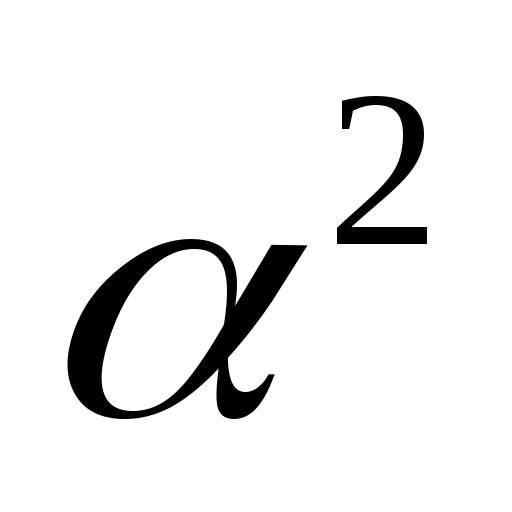. При умножении 
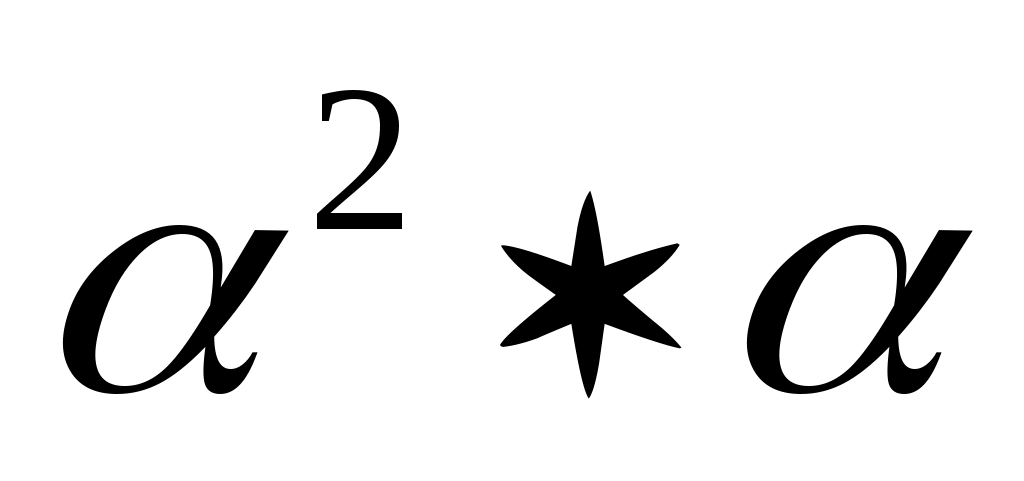мы умножаем точки Р и N (по определению умножения фигур), значит, все точки отрезка PN принадлежат фигуре 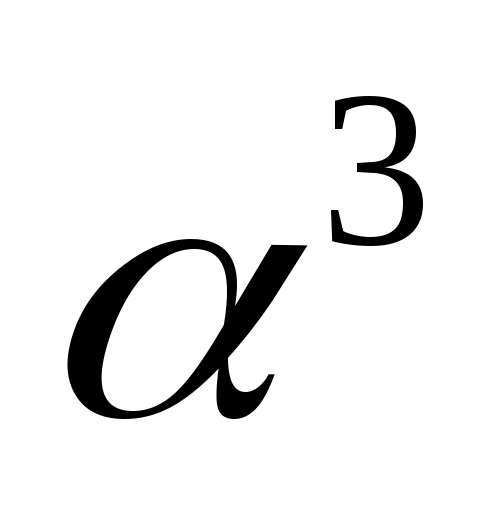, следовательно, и отрезок АВ принадлежит этой фигуре. Теорема доказана.
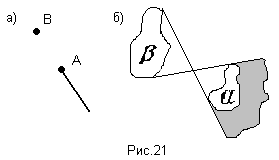
Частное А/В двух точек – это луч с началом А, продолжение которого проходит через В. (или тень, отбрасываемая “колышком” А, освещенным “фонариком” В. (рис.21а).
Аналогично , частное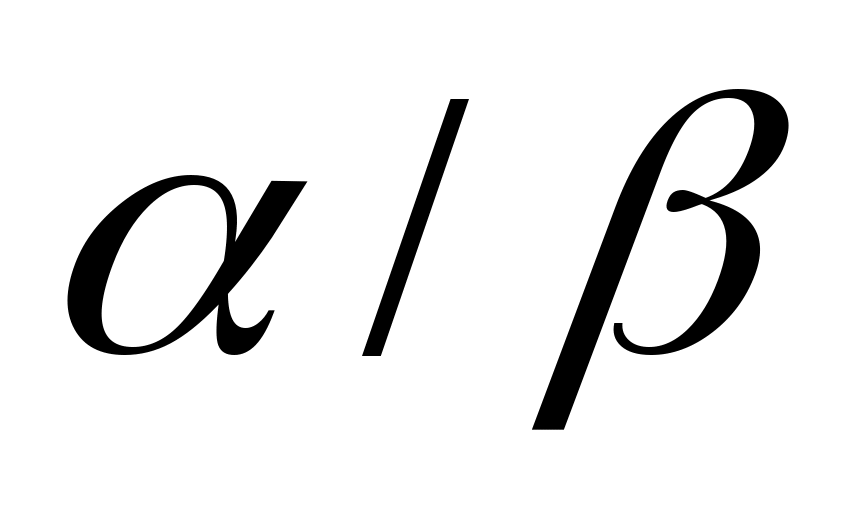
двух фигур – это объединение всех лучей А/В, где А принадлежит , а В принадлежит 
. (рис.21б)
Свойства деления точек А, В и С:
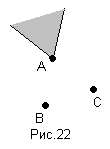
А) (А/В)/С=А/(ВС) (рис.22)
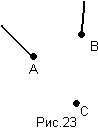
Б) (А+В)/С=(А/С)+(В/С) (рис.23)
В) А/(В+С)=(А/В)+(А/С) (рис.24)
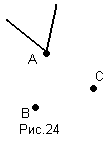
Г) (АВ)/С=(А/С)(В/С) (рис.25)
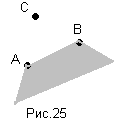
Д) А/(ВС)=(А/В)(А/С) (рис.26).
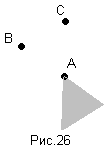
Для доказательства теорем нам понадобится лемма, доказательство которой очевидно.
Лемма (о делении фигур самих на себя).Результат деления любой фигуры саму на себя содержит эту фигуру.
Далее рассмотрены крайние случаи: когда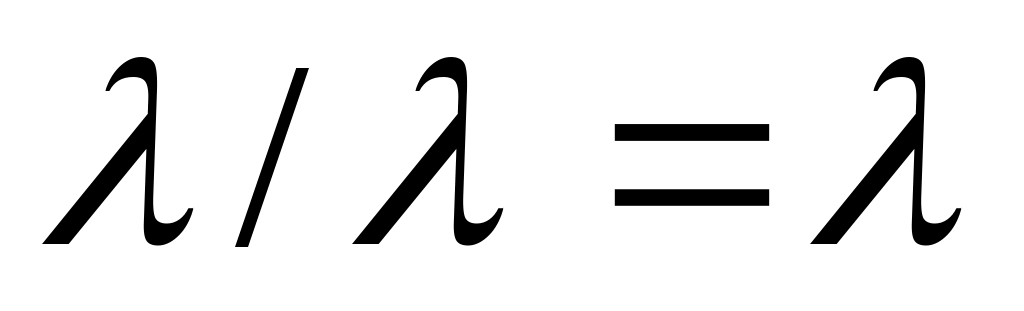
(в этом случае фигуру называют линейной) и когда 
.
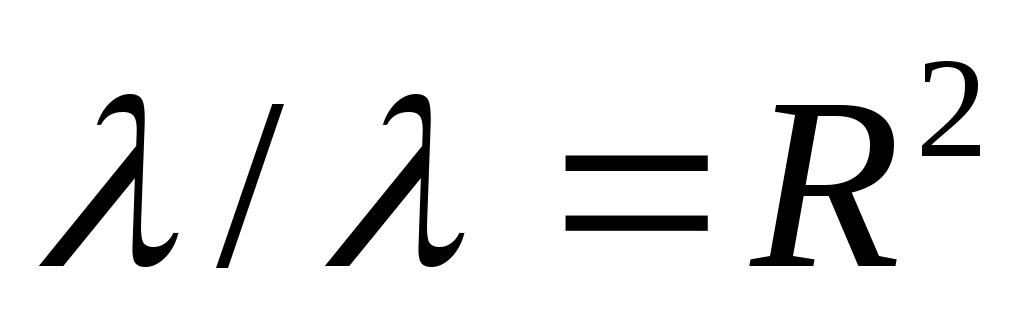Теорема (о линейных фигурах).Все линейные фигуры плоскости исчерпываются точками, прямыми и всей плоскостью.
Доказательство.Если фигура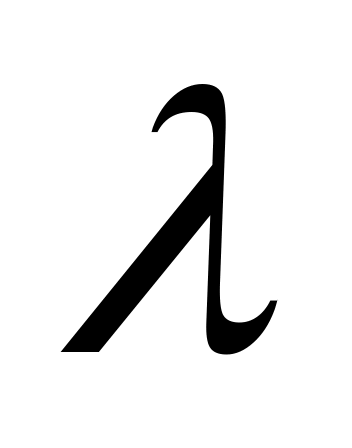
содержит более одной точки, то результат деления 
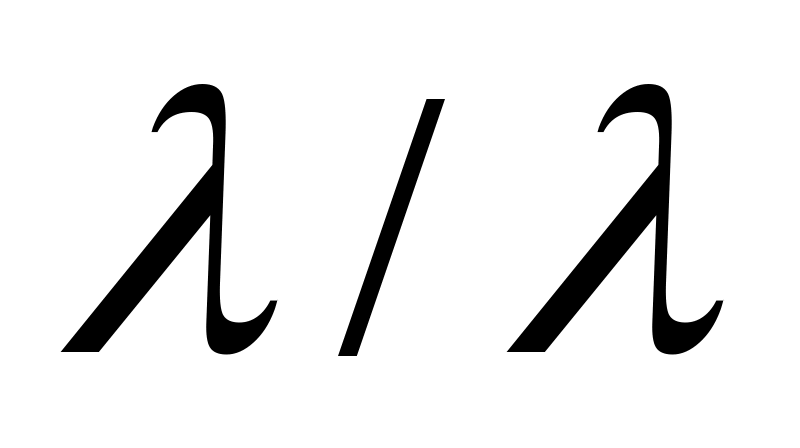будет содержать как минимум два луча. Лучи – фигуры неограниченные, а значит, линейные фигуры – это фигуры неограниченные (за исключением случая точки – при делении точки А самой на себя мы получаем “слившийся” с точкой А луч).
Возьмем две точки А и В. При делении этих точек самих на себя мы получаем лучи с началами в этих точках, лежащие на прямой АВ. В одномерном пространстве возможны два варианта, соответствующих этим условиям: прямая и луч.
При делении луча самого на себя мы получаем прямую, а при делении прямой самой на себя – эта же прямая. В нульмерном пространстве вариант один: точка, а результат деления точки самой на себя является, как уже упомянуто выше, лучом, слившимся с этой точкой, т.е., этой точкой, и точка является линейной фигурой.
Рассмотрим двухмерное пространство. В нем тоже возможны варианты неограниченных множеств: части плоскости, ограниченные прямой, лучами, кривыми… В любой части плоскости всегда найдутся три точки, не лежащие на одной прямой. При делении трех точек самих на себя мы получим 6 лучей, являющихся продолжениями отрезков сторон треугольника, образованного этими точками. Всегда найдется при этом луч, выходящий за пределы рассмотренной части плоскости. Таким образом, вся плоскость также является линейной фигурой.
Таким образом, все линейные фигуры плоскости исчерпываются точками, прямыми и всей плоскостью. Теорема доказана.
Теорема (о делении фигур с ненулевой площадью самих на себя).Результатом деления любой фигуры с ненулевой площадью самой на себя всегда является вся плоскость.
Доказательство.Возьмем некоторую фигуру
с ненулевой площадью. Для доказательства теоремы нам достаточно доказать, что результат деления 
содержит любую точку А, не принадлежащую фигуре .В любую фигуру с ненулевой площадью можно вписать окружность, с центром в некоторой точке О. Как известно, через любые две точки можно провести прямую, и притом только одну. Проведем прямую ОА. Эта прямая обязательно пересечет окружность в некоторой точке С. Т.к. окружность является подмножеством фигуры , то при делении мы обязательно поделим точку С на точку О (по определению деления фигур), а так как точка С принадлежит прямой ОА, то результат деления С/О будет содержать точку А, а значит, и результат деления
будет содержать эту точку. Вся плоскость состоит из бесконечного количества таких точек А, и для каждой из них будет действовать выше доказанное. Теорема доказана.
Список литературы
-
Задачи
В данном пункте приведены примеры умножения различных фигур.
На рисунке 18 показано умножение точки на отрезок.
На рисунке 19 – результат умножения квадрата на круг.
На рисунке 20 вы можете увидеть результат умножения точки на круг на прямоугольник.
Натуральная степень фигур.
В арифметике и в алгебре особую роль играют те числа, квадрат которых равен им самим. Ясно, что этим свойством обладают лишь два числа: 1 и 0.
В мультипликативной геометрии этим свойством обладают выпуклые фигуры. Фигура – это произвольное множество точек плоскости. Выпуклая оболочка фигуры – это наименьшая степень, при возведении в которую мы получаем выпуклую фигуру.
Теорема (о выпуклой оболочке плоских фигур).Выпуклой оболочкой любой фигуры на плоскости будет ее третья степень.
Доказательство.Пусть точки А и В принадлежат фигуре
. Для доказательства теоремы нам достаточно доказать, что отрезок АВ будет подмножеством этой фигуры. Пусть точки А и В принадлежат отрезку PN, причем Р принадлежит фигуре , а точка N – фигуре . Т.к. произведение любой фигуры саму на себя содержит эту фигуру, то точки Р и N принадлежат фигуре . При умножении мы умножаем точки Р и N (по определению умножения фигур), значит, все точки отрезка PN принадлежат фигуре , следовательно, и отрезок АВ принадлежит этой фигуре. Теорема доказана.-
Деление фигур на плоскости-
Определение и свойства деления фигур.
-
Частное А/В двух точек – это луч с началом А, продолжение которого проходит через В. (или тень, отбрасываемая “колышком” А, освещенным “фонариком” В. (рис.21а).
Аналогично , частное
двух фигур – это объединение всех лучей А/В, где А принадлежит , а В принадлежит . (рис.21б) Свойства деления точек А, В и С:
А) (А/В)/С=А/(ВС) (рис.22)
Б) (А+В)/С=(А/С)+(В/С) (рис.23)
В) А/(В+С)=(А/В)+(А/С) (рис.24)
Г) (АВ)/С=(А/С)(В/С) (рис.25)
Д) А/(ВС)=(А/В)(А/С) (рис.26).
-
Теоремы о частном
Для доказательства теорем нам понадобится лемма, доказательство которой очевидно.
Лемма (о делении фигур самих на себя).Результат деления любой фигуры саму на себя содержит эту фигуру.
Далее рассмотрены крайние случаи: когда
(в этом случае фигуру называют линейной) и когда . Теорема (о линейных фигурах).Все линейные фигуры плоскости исчерпываются точками, прямыми и всей плоскостью.
Доказательство.Если фигура
содержит более одной точки, то результат деления будет содержать как минимум два луча. Лучи – фигуры неограниченные, а значит, линейные фигуры – это фигуры неограниченные (за исключением случая точки – при делении точки А самой на себя мы получаем “слившийся” с точкой А луч).
Возьмем две точки А и В. При делении этих точек самих на себя мы получаем лучи с началами в этих точках, лежащие на прямой АВ. В одномерном пространстве возможны два варианта, соответствующих этим условиям: прямая и луч.
При делении луча самого на себя мы получаем прямую, а при делении прямой самой на себя – эта же прямая. В нульмерном пространстве вариант один: точка, а результат деления точки самой на себя является, как уже упомянуто выше, лучом, слившимся с этой точкой, т.е., этой точкой, и точка является линейной фигурой.
Рассмотрим двухмерное пространство. В нем тоже возможны варианты неограниченных множеств: части плоскости, ограниченные прямой, лучами, кривыми… В любой части плоскости всегда найдутся три точки, не лежащие на одной прямой. При делении трех точек самих на себя мы получим 6 лучей, являющихся продолжениями отрезков сторон треугольника, образованного этими точками. Всегда найдется при этом луч, выходящий за пределы рассмотренной части плоскости. Таким образом, вся плоскость также является линейной фигурой.
Таким образом, все линейные фигуры плоскости исчерпываются точками, прямыми и всей плоскостью. Теорема доказана.
Теорема (о делении фигур с ненулевой площадью самих на себя).Результатом деления любой фигуры с ненулевой площадью самой на себя всегда является вся плоскость.
Доказательство.Возьмем некоторую фигуру
с ненулевой площадью. Для доказательства теоремы нам достаточно доказать, что результат деления содержит любую точку А, не принадлежащую фигуре .В любую фигуру с ненулевой площадью можно вписать окружность, с центром в некоторой точке О. Как известно, через любые две точки можно провести прямую, и притом только одну. Проведем прямую ОА. Эта прямая обязательно пересечет окружность в некоторой точке С. Т.к. окружность является подмножеством фигуры , то при делении мы обязательно поделим точку С на точку О (по определению деления фигур), а так как точка С принадлежит прямой ОА, то результат деления С/О будет содержать точку А, а значит, и результат деления
будет содержать эту точку. Вся плоскость состоит из бесконечного количества таких точек А, и для каждой из них будет действовать выше доказанное. Теорема доказана. Список литературы
-
Рыжик В. Давайте складывать точки // Квант. – № 1 – 1976 -
Яглом И. Соединим две точки отрезком // Квант. – № 4 – 1981 -
“Арифметика фигур” /Статья “Векторы и их применение в геометрии”. Энциклопедия элементарной математики, т.IV. -
Геометрия 7 – 9: Учебник для общеобразовательных учреждений./ Л. С. Анастасян, Б. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина. – 13-е издание – М.; Просвещение, 2003.