3 подслучай: объединение неограниченно на обоих лучах. Независимо от способа умножения результатом будет объединение лучей, на которых объединение фигур неограниченно.

3 случай: объединение фигур лежит на трех лучах.

1 подслучай: объединение ограниченно на всех трех лучах. Определим наиболее удаленные от центра универсума точки на каждом из лучей. Независимо от способа умножения результатом будет объединение отрезков, соединяющих центр универсума с наиболее удаленными точками на каждом луче.

2 подслучай: объединение ограниченно на двух лучах и неограниченно на третьем. Определим наиболее удаленные от центра универсума точки на лучах, на которых объединение фигур ограниченно. Независимо от способа умножения результатом будет объединение отрезка, соединяющего эти точки, и луча, на котором юбъединение исходных фигур неограниченно.

3 подслучай: объединение ограниченно на одном луче и неограниченно на двух других. Определим наиболее удаленную от центра универсума точку на луче, на котором объединение фигур ограниченно. Независимо от способа умножения результатом будет объединение отрезка, соединяющего эту точку с центром универсума. и лучей, на которых объединение фигур неограниченно.

4 подслучай: объединение неограниченно на всех трех лучах. Независимо от способа умножения результатом будет весь универсум.

Свойство доказано.

Д) Идемпотентность

В трехлучевом пространстве она действительна только для выпуклых фигур, определение которых совпадает со связными, т.к:

Выпуклая фигура – это такая фигура, любые две точки которой можно соединить отрезком, целиком принадлежащим исходной фигуре.

Связная фигура – это такая фигура, у которой любые две точки можно соединить ломаной, лежащей целиком в этой фигуре.

Изначально мы зафиксировали, что определения отрезка и ломаной в трехлучевой арифметике совпадают, значит, совпадают и определения связных и выпуклых фигур.

Что же касается идемпотентности выпуклых фигур, то это свойство очевидно – любые две точки связной фигуры уже можно соединить лежащим внутри нее отрезком, поэтому уже не будет содержать какой-то новой точки.

, где

---

- выпуклая (связная) фигура.

В случае, если фигура - невыпуклая, свойство не действует. Примером является случай, когда фигура состоит из двух точек, не совпадающих друг с другом. Результатом умножения будет являться отрезок, соединяющий эти точки; он не совпадет с исходной фигурой.

Интересно рассмотреть аналог выпуклой оболочки фигуры из моей прошлой работы.

Выпуклая оболочка фигуры – это наименьшая степень, при возведении в которую фигура становится выпуклой.

Теорема (о выпуклой оболочке фигур в трехлучевом пространстве)

Выпуклой оболочкой любой фигуры в трехлучевом пространстве будет ее вторая степень.

Доказательство

Пусть точки А и В принадлежат несвязной фигуре , причем не все точки отрезка АВ принадлежат этой фигуре. Умножим фигуру саму на себя; по определению умножения мы перемножим точки А и В, тогда отрезок АВ будет являться подмножеством , то есть - всегда выпуклая фигура, а вторая степень – это выпуклая оболочка фигуры .

Теорема доказана

4. 
   Понятие деления. Свойства деления
   

В обычной, числовой арифметике деление является обратной умножению операцией, в трехлучевой же арифметике результатом деления А на В будет являться такая фигура , результат умножения которой на В будет всегда содержать точку А. Так как нам нужен определяющийся единственным образом результат, то вы можете видеть различные варианты частного А/В, в зависимости от расположения точек А и В.(рис.6) На рисунке 6а точки А и В лежат на одном луче, причем точка А более удалена от центра универсума, чем точка В; на рисунке 6б точки А и В лежат на разных лучах; на рисунке 6в точки А и В лежат на одном луче, но точка В более удалена от центра универсума, чем точка А.

---

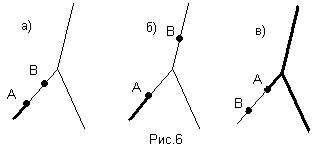
Такое деление точек обладает несколькими свойствами:

А) (А/В)/С=А/(ВС). Свойство доказано графически (рис.7)



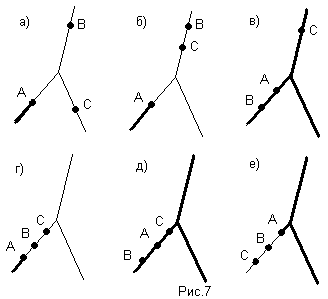
Б) (А+В)/С=(А/С)+(В/С). Свойство доказано графически (рис.8).



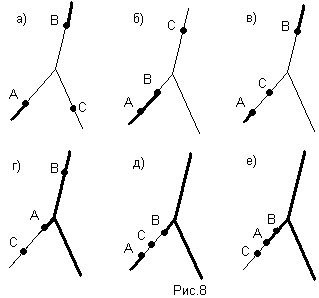
Следующие три свойства не существуют для арифметики чисел:

В) А/(В+С)=(А/В)+(А/С). (рис.9)



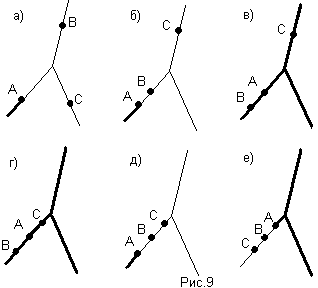
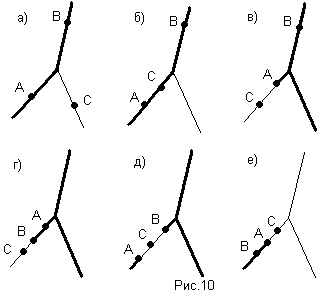
Г) (АВ)/С=(А/С)(В/С). (рис.10)



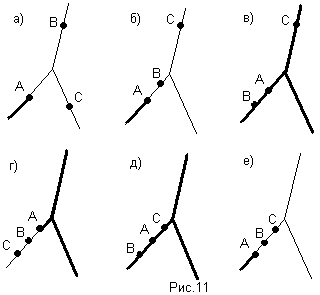
Д) А/(ВС)=(А/В)(А/С). (рис.11)



Аналогично определению деления точек следует определение деления фигур – для того, чтобы получить частное , нужно поделить все точки фигуры на все точки фигуры .

5. 
   Деление фигур самих на себя
   

В прошлом году особое внимание в делении фигур самих на себя привлекли два крайних случая результата – когда и когда .

Рассмотрим первый случай.

Теорема(о линейных фигурах)

Линейными фигурами в трехлучевом пространстве являются точка и весь универсум.

Доказательство.

То, что эти фигуры являются линейными, очевидно – результат деления точки самой на себя – это луч с началом в этой точке и с продолжением в ней же, т.е. сама точка. При делении универсума самого на себя мы не можем получить что-то, выходящее за его пределы – но, так как результат деления фигуры саму на себя содержит эту фигуру, мы получим в результате деления сам универсум.

В случае с остальными фигурами поделим их на связные и несвязные. При делении связной фигуры самой на себя (исключая случай одной точки) мы получим весь универсум, а не исходную фигуру. При делении несвязной фигуры самой на себя мы получим либо универсум (если в ней есть связное подмножество), или же какую-то другую несвязную фигуру.

---

Линейные фигуры исчерпываются точкой и универсумом.

Теорема доказана.

Относительно случая, где частным является универсум, действует следующая теорема:

Теорема (о частном, совпадающем с универсумом).

Результат деления фигуры самой на себя совпадает с универсумом, если фигура содержит связное подмножество.

Доказательство.

Рассмотрим фигуру , содержащую связный элемент. Из этого элемента можно выделить отрезок. При делении мы поделим этот отрезок сам на себя, а так как результатом деления отрезка самого на себя является универсум, то и результатом деления будет универсум.

Теорема доказана.

2. 
   Мультипликативная арифметика фигур
   
   1. 
      Умножение точек и фигур на плоскости
      
      1. 
         Свойства умножения
         

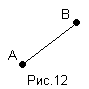
Отрезок с концами А и В часто обозначается символом АВ (рис.12). Эта запись подсказывает неожиданную терминологию: отрезок АВ назовем произведением точек А и В.



Аналогично, произведением фигур и мы назовем объединения всех возможных произведений точек фигуры на точки фигуры . Умножение точек обладает следующими свойствами:

а) Умножение точек коммутативно

АВ=ВА.

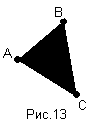
б) Умножение точек ассоциативно

(АВ)С=А(ВС) Это свойство проиллюстрировано на рисунке 13.



в) Умножение точек дистрибутивно относительно их сложения.

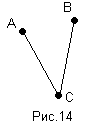
(А+В)С=АС+ВС. Под сложением точек А и В мы подразумеваем объединение точек А и В. Это свойство проиллюстрировано на рисунке 14.



г) Умножение фигур идемпотентно

---

, т.е АА – отрезок со слившимися концами, т.е. сама точка А.

Первые три свойства переносятся и на произвольные фигуры:

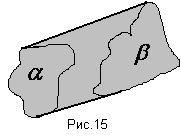
А) Умножение фигур коммутативно (рис.15), очевидно из определения.



Б) умножение фигур ассоциативно

(АВ)С=А(ВС)

В)Умножение фигур дистрибутивно относительно их сложения. А(В+С)=АВ+АС. Под понятием сложения подразумевается объединение отрезков.

Г) Несмотря на то, что идемпотентность умножения фигур места не имеет, верно следующее свойство: произведение любой фигуры самой на себя содержит эту фигуру как подмножество, т.е. (рис.16)



Некоторыми замечательными свойствами обладает особая категория фигур – выпуклые фигуры. В данной статье выпуклая фигура определяется как фигура, любые две точки которой можно соединить отрезком, все точки которого принадлежат данной фигуре.

Теорема (об умножении выпуклых фигур).Произведение двух выпуклых фигур выпукло. (Выпуклая фигура – это такая фигура, любые две точки которой можно соединить отрезком, который целиком принадлежит этой фигуре).



Доказательство (от противного). Возьмем две произвольные выпуклые фигуры и (Рис.17). Предположим, что их произведение не выпукло, тогда имеются хотя бы две точки , , которые мы не можем соединить отрезком, принадлежащим данной фигуре. Но по определению произведения фигур - это объединение всех отрезков, соединяющих всевозможные точки фигур и

---

Смотрите также файлы

• Контрольноизмерительный материал для проведения промежуточной аттестации обучающихся 10 класса по Информатике и икт за 2019 2020 учебный год Спецификация контрольных измерительных материалов Назначение ким.docx

• Задание Философия и ее роль в жизни и обществе i впишите пропущенные термины, слова и имена.docx

• Тема Зоопсихология как научная.docx

• В. Ю. Бабошкин 20 г.docx

• "АлтынЕмель" в наследие юнеско включён.docx