МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ,СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)Кафедра информационных управляющих системЛабораторная работа № 5«Обработка экспериментальных данных»Варианты 1, 6, 7Работу выполнил студент гр. ИСТ-112:Агарков В.А., Мельников М.А., Дерендяев К.С.Проверил __________________Эль Сабаяр Шевченко Н.(оценка и подпись)Санкт-Петербург2023Формулировка заданияДаны два задания. Оба требуется решить в 1, 6, 7 вариантах.В результате эксперимента была определена некоторая табличная зависимость. С помощью метода наименьших квадратов определить линию регрессии, рассчитать коэффициент корреляции, подобрать функциональную зависимость заданного вида, вычислить коэффициент регрессии. Определить суммарную ошибку.Задание 1Вариант 1.Вариант 6.Вариант 7.Задание 2. 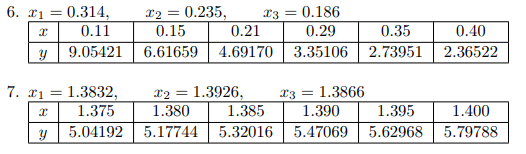Найти приближенное значение функции при заданном значении аргумента с помощью функции линейной интерполяции.Функция задана таблично.Вариант 1.Варианты 6, 7.Теоретический материал

---

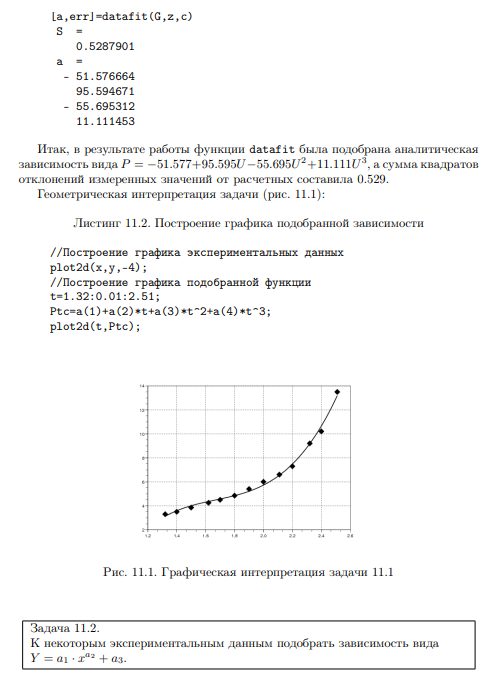
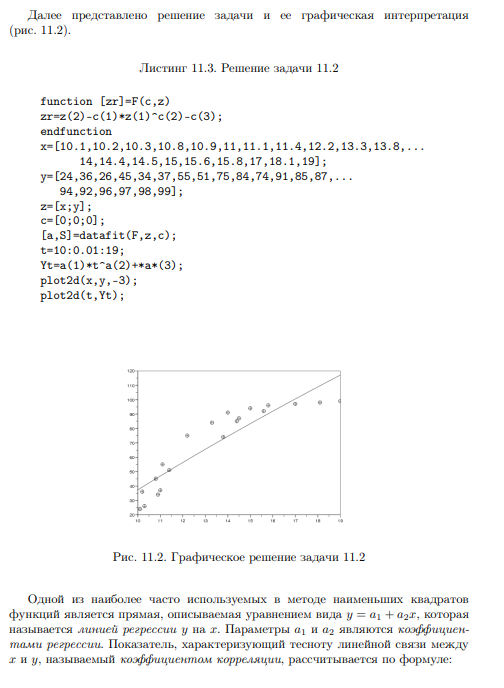
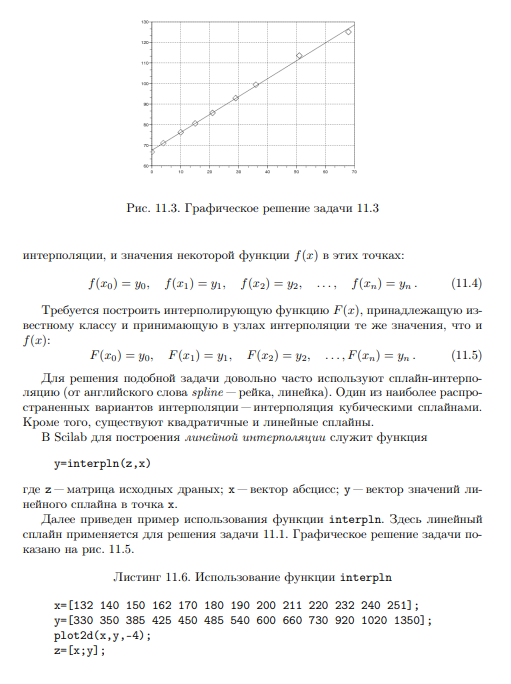
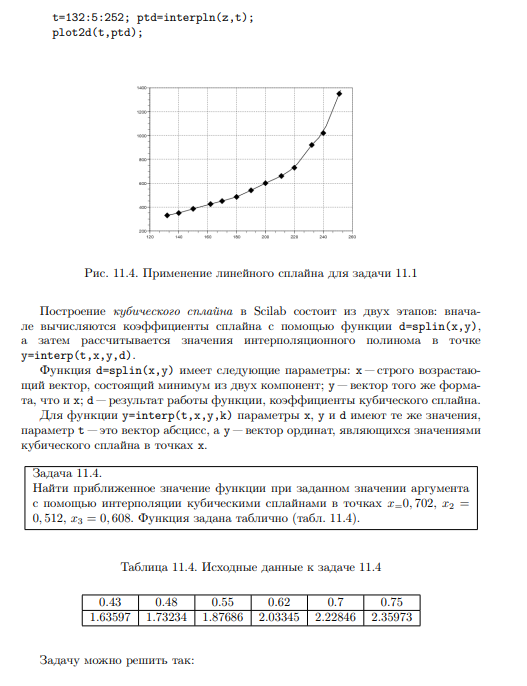
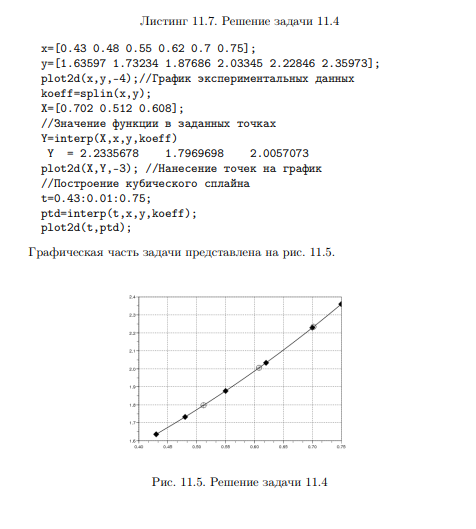
Ход работыЛистинг код решения задачЗадание 1:clear, clf, clc // Подбираем функциональную зависимостьfunction y=F(x,с) // Искомая функцияy=с(1)*x^3 + с(2)*x^2 + c(4);endfunctionfunction [err]=G(c,z) // Функция вычисления ошибки мнкh = z(1,:);R = z(2,:);err = R - F(h,c);endfunctionx = [0 1 1.5 2 2.5 3 3.5 4 4.5 5]; // Исходные данныеy = [12 10.1 11.58 17.4 30.68 53.6 87.78 136.9 202.5 287];z = [x; y];c = [1;1;1;1];[k, l] = reglin(x, y); // Коэффициенты регрессии[a,err] = datafit(G,z,c) // Суммарная ошибкаr = sum((x-mean(x)).*(y-mean(y)))/sqrt(sum((x-mean(x))^2)*sum((y-mean(y))^2))// Решение задачиplot2d(x,y,style=-9)plot2d(x, F(x,a), style=2)plot2d(x, k*x+l)xgrid(color('grey75'))title(['error = ',string(err)])Вариант 1.clear, clf, clc // Подбираем функциональную зависимостьfunction y=F(x,с) // Искомая функцияy=x./(c(1).*x - c(2));endfunctionfunction [err]=G(c,z) // Функция вычисления ошибки мнкh = z(1,:);R = z(2,:);err = R - F(h,c);endfunctionx = [3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9]; // Исходные данныеy = [0.61 0.6 0.592 0.58 0.585 0.583 0.582 0.57 0.572 0.571];z = [x; y];c = [1;1;1;1];[k, l] = reglin(x, y); // Коэффициенты регрессии[a,err] = datafit(G,z,c) // Суммарная ошибкаr = sum((x-mean(x)).*(y-mean(y)))/sqrt(sum((x-mean(x))^2)*sum((y-mean(y))^2)) // Коэфф корреляции// Решение задачиplot2d(x,y,style=-9)plot2d(x, F(x,a), style=2)plot2d(x, k*x+l)xgrid(color('grey75'))title(['error = ',string(err)])Вариант 6.clear, clf, clc // Подбираем функциональную зависимостьfunction y = F(x, c) // Искомая функция

---

y = 1 ./ (c(1) + c(2) .* exp(-x));

endfunction

function [err]=G(c,z) // Функция вычисления ошибки мнк

h = z(1,:);

R = z(2,:);

err = R - F(h,c);

endfunction

x = [0 1 1.5 2 2.5 3 3.5 4 4.5 5]; // Исходные данные

y = [12 10.1 11.58 17.4 30.68 53.6 87.78 136.9 202.5 287];

z = [x; y];

c = [1;1];

[k, l] = reglin(x, y); // Коэффициенты регрессии

[a,err] = datafit(G,z,c) // Суммарная ошибка

r = sum((x-mean(x)).*(y-mean(y)))/sqrt(sum((x-mean(x))^2)*sum((y-mean(y))^2)) // Коэфф корреляции

// Решение задачи

plot2d(x,y,style=-8)

plot2d(x, F(x,a'), style=1)

plot2d(x, k*x+l)

xgrid(color('grey75'))

title(['err = ',string(err)])

Вариант 7.

Задание 2:

clear, clf, clc

x=[0.43 0.48 0.55 0.62 0.7 0.75];

y=[1.63597 1.73234 1.87686 2.03345 2.22846 2.35973];

z = [x;y];

plot2d(x,y,-4);

koeff=splin(x,y);

X=[0.702 0.512 0.608];

Y=interp(X,x,y,koeff)

plot2d(X,Y,-3);

t=0.43:0.01:0.75;

ptd=interpln(z, t);

plot2d(t,ptd);

Вариант 1.

clear, clf, clc

x=[0.11 0.15 0.21 0.29 0.35 0.40];

y=[9.05421 6.61659 4.69170 3.35106 2.73951 2.36522];

z = [x;y];

plot2d(x,y,-4);

koeff=splin(x,y);

X=[0.314 0.235 0.186];

Y=interp(X,x,y,koeff)

plot2d(X,Y,-3);

t=0.11:0.01:0.40;

ptd=interpln(z, t);

plot2d(t,ptd);

Вариант 6.

clear, clf, clc

x=[1.375 1.380 1.385 1.390 1.395 1.400];

y=[5.04192 5.17744 5.32016 5.47069 5.52968 5.79788];

z = [x;y];

plot2d(x,y,-4);

koeff=splin(x,y);

X=[1.3832 1.3926 1.3866];

Y=interp(X,x,y,koeff)

plot2d(X,Y,-3);

t=1.375:0.01:1.400;

ptd=interpln(z, t);

plot2d(t,ptd);

Вариант 7.

Результат выполнения работы

Задание 1:



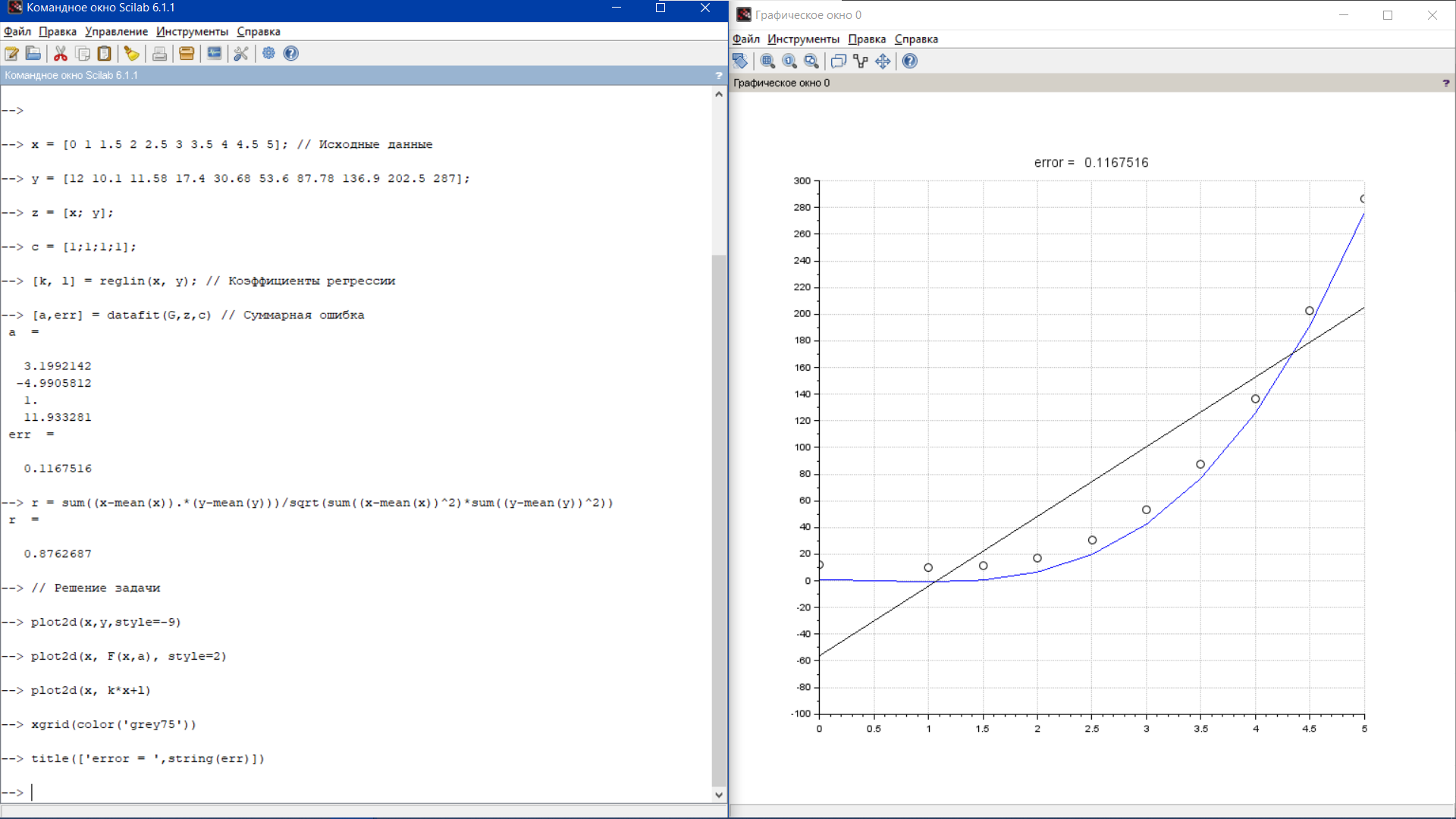
Вариант 1.



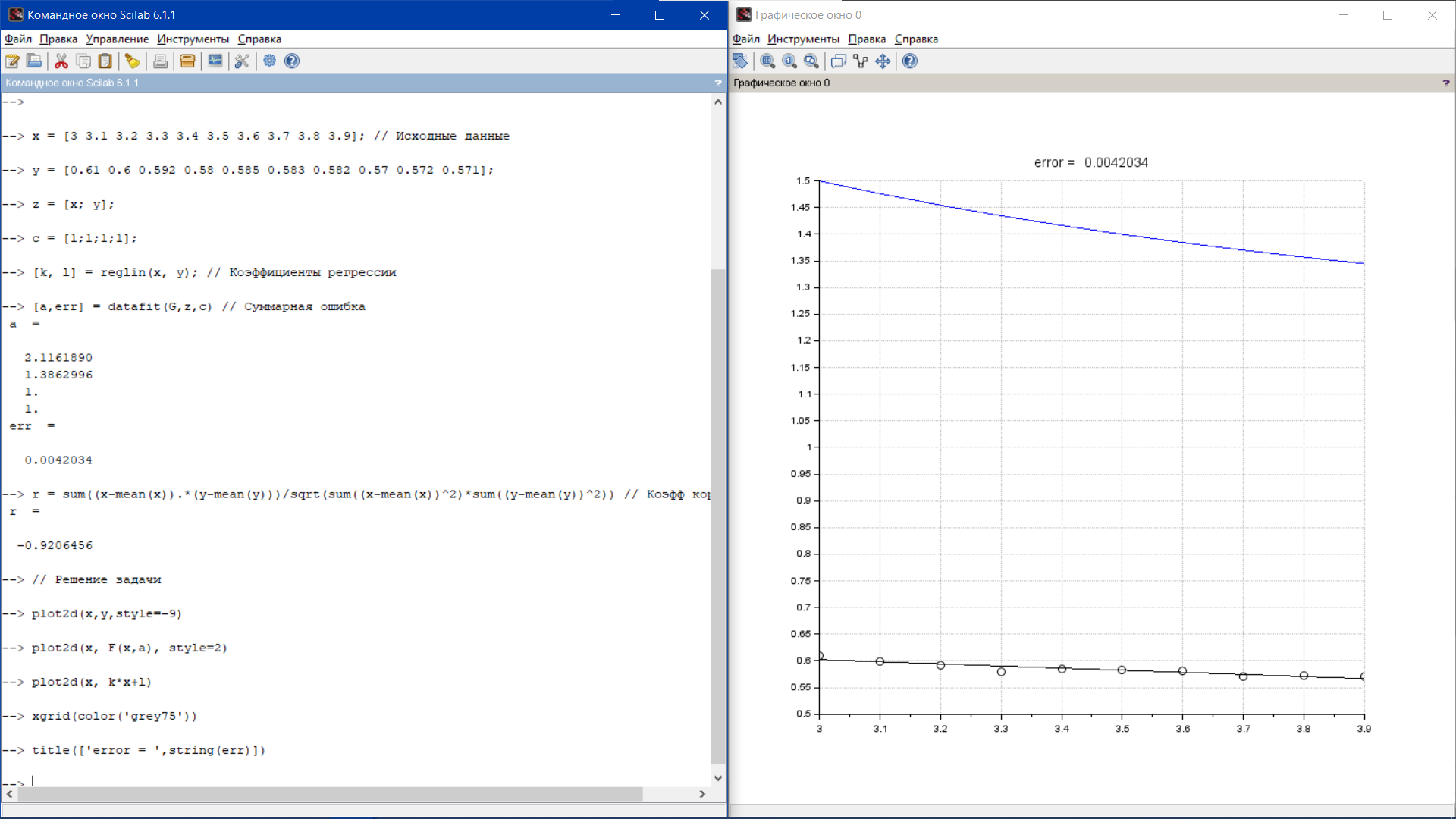
Вариант 6.



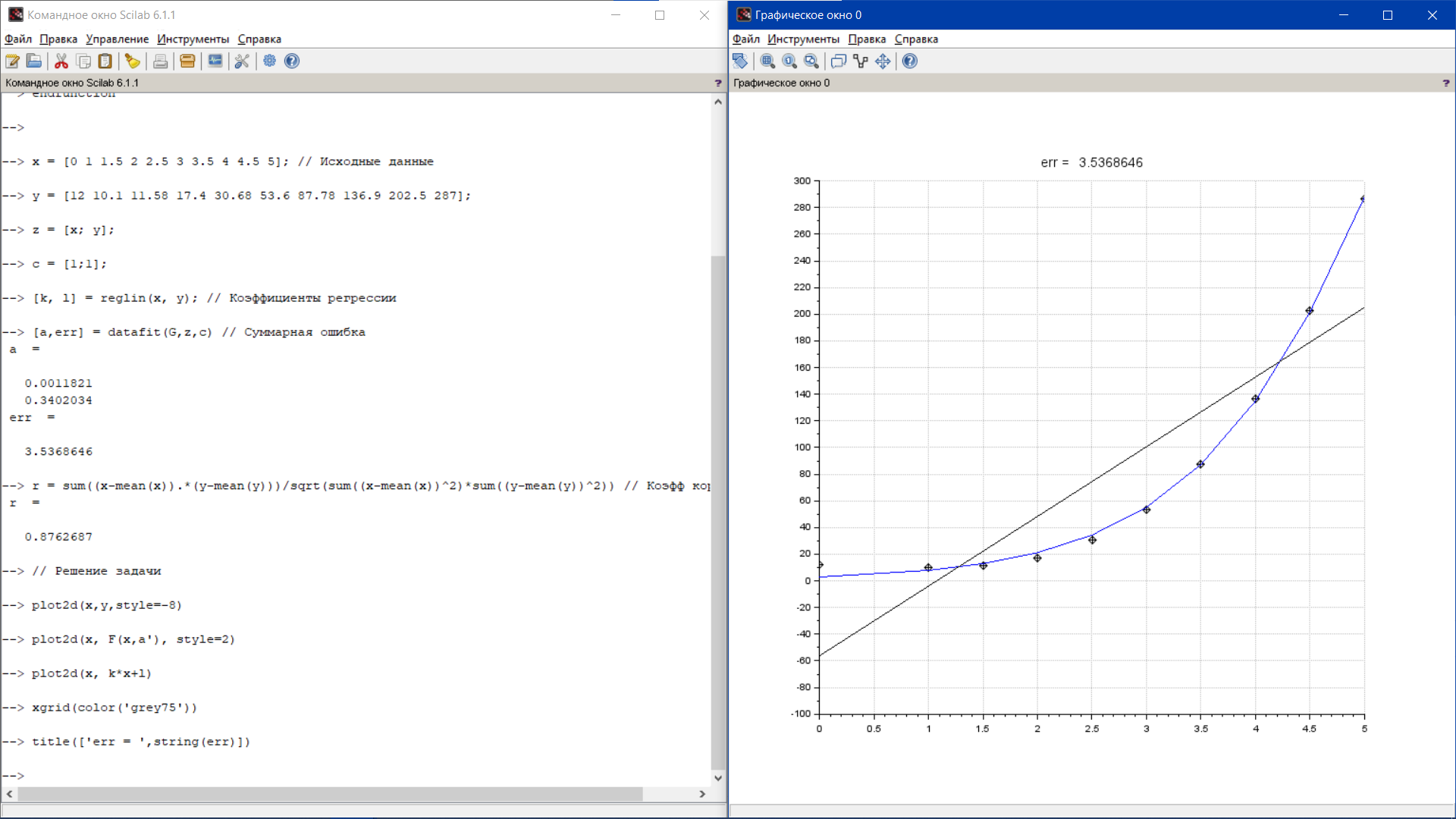
Вариант 7.

Задание 2:



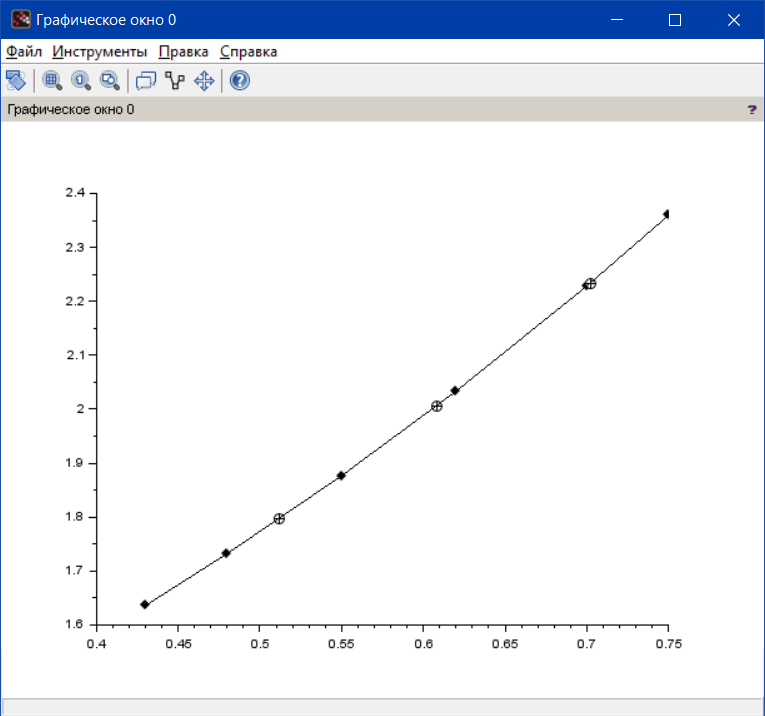
Вариант 1.



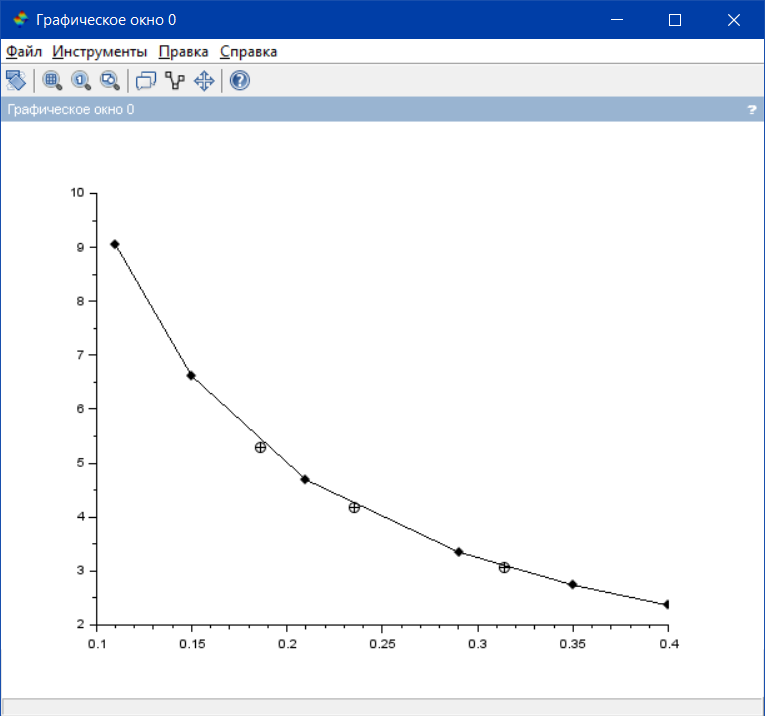
Вариант 6.



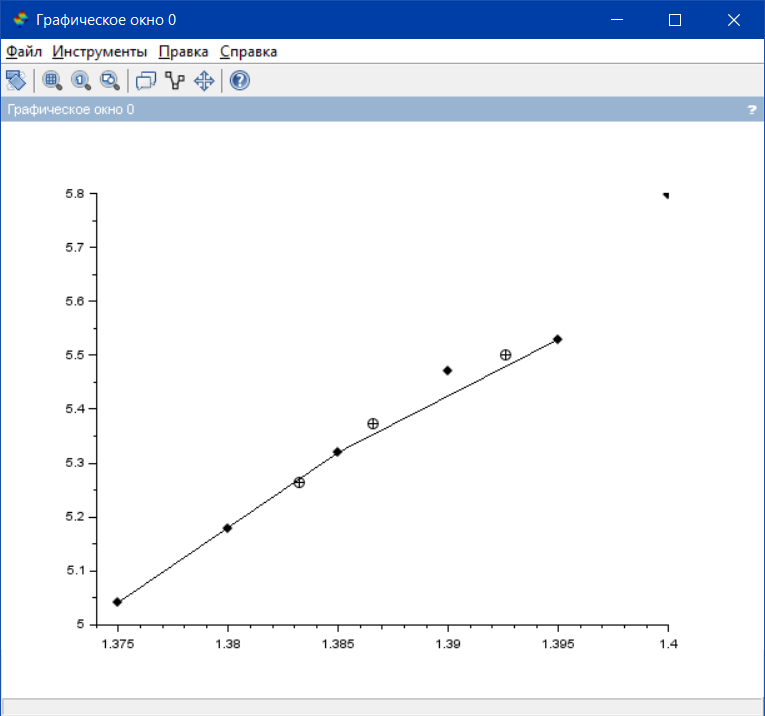
Вариант 7.
Вывод:

В ходе выполнения лабораторной работы была успешно определена табличная зависимость и вычислены необходимые параметры, такие как линия регрессии, коэффициент корреляции, функциональная зависимость заданного вида, коэффициент регрессии и суммарная ошибка. Была проведена функция линейной интерполяции, которая позволила найти приближенное значение функции при заданном значении аргумента. Результаты эксперимента могут быть использованы в дальнейшей работе, например, для предсказания будущих значений величины или для анализа зависимостей в данных.

---

Смотрите также файлы

• Моё здоровье. Личная гигиена.doc

• Отчет по самообследованию мбоу Банновская основная общеобразовательная школа.pdf

• Реферат по физкультуре. Тема упражнения для подготовки игрока по настольному теннису.docx

• !186768 жылдардаы реформа бойынша Тркістан губернаторына дипломатиялы келісім жасауа ы берілді.docx

• Методические указания по выполнению курсовых работ по дисциплине Основы предпринимательского и коммерческого права.doc