Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Эконометрика

МОСКВА 2023

ЗАДАНИЕ ПО ПРАКТИЧЕСКОЙ РАБОТЕ
Вопросы:

1. 
   Укажите основные этапы эконометрического исследования.
   

Ответ: к основным этапам эконометрического исследования можно отнести следующие: построение эконометрических моделей, т.е. представление экономических связей в математической форме (этап спецификации); оценка параметров построенной модели (этап параметризации); проверка качества найденных параметров модели и самой модели в целом (этап верификации); использование построенных моделей, например для прогнозирования и предсказаний, и, в конечном счете, проведения экономической политики.

2. 
   Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей.
   

Ответ: виды аналитических зависимостей, наиболее часто используемых при построении моделей:

3. 
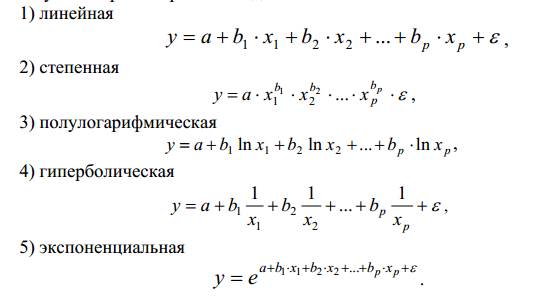
   Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии.
   

Ответ: парной регрессией называется уравнение связи двух переменных у и х вида y = f(x), где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор). Различают линейные и нелинейные регрессии. Линейная регрессия описывается уравнением: y = a + b·x + ε. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в а нализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

---

Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам: – полиномы разных степеней ŷ x = a + b 1 · x + b2 · x 2 + b3 · x 3 + ε; – равносторонняя гипербола ŷ x =a +b/x + ε. Примеры регрессий, нелинейных по оцениваемым параметрам: – степенная ŷ x = a ·x b ·ε; – показательная ŷ x = a ·b x ·ε; – экспоненциальная ŷ x =e a+b x ·ε. Наиболее часто применяются следующие модели регрессий: – прямой ŷ x = a + b·x; – гиперболы ŷ x = a + b / x ; – параболы ŷ x = a + b·x+ c·x 2 ; – показательной функции ŷ x = a·b x ; – степенная функция ŷ x= а·х b · и др.

Парная регрессия применяется, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Применяется три основных метода выбора вида аналитической зависимости: – графический (на основе анализа поля корреляций); – аналитический, т. е. исходя из теории изучаемой взаимосвязи; – экспериментальный, а именно, путем сравнения величины остаточной дисперсии Dост или средней ошибки аппроксимации A, рассчитанных для различных моделей регрессии (метод перебора)

4.Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции r_xy .

Ответ: тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rxy для линейной регрессии (–1 ≤ rxy ≤ 1) (1.3) и индекс корреляции ρxy для нелинейной регрессии (0 ≤ ρxy ≤ 1) (1.4) Имеет место соотношение 7 Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации r 2 xy (для линейной регрессии) или индекс детерминации R 2 = ρ 2 xy (для нелинейной регрессии).

Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции rxy применяется t-критерий Стьюдента и рассчитываются доверительные интервалы каждого из показателей. Согласно t-критерию выдвигается гипотеза Н0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия tфакт для оцениваемых коэффициентов регрессии и коэффициента корреляции rxy путем сопоставления их значений с величиной стандартной ошибки

5.Объясните сущность метода анализа динамического ряда.

Ответ: Динамический ряд – это ряд статистических величин, которые воспроизводят изменения явления во времени и расположенны в хронологическом порядке через определенные промежутки времени. Составляющими частями динамического ряда являются его уровни и интервалы - показатели времени (годы, кварталы, месяцы, и так далее) или моменты (периоды времени).

---

Задачи

1. 
   Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3
   

Таблица 3. Регрессионный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

2. 
   Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4.
   

Таблица 4. Корреляционный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

---

Смотрите также файлы

• Практическая работа 6 Постановка судна на один и на два якоря.docx

• День предмет.docx

• Протокол 2022 г. Согласовано Заместитель директора маноу ок Слобожанщина.docx

• Sabirova S. G. (Branch of Moscow State University named M. V. Lomonosov, Dushanbe, Tajikistan).docx

• Падежи имён существительных Именительный падеж.ppt