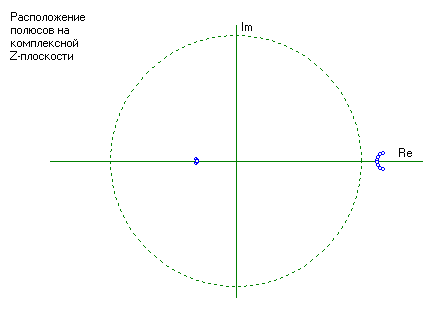
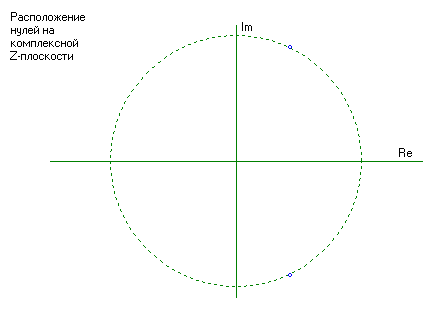
Рисунок 8 - Картина нулей и полюсов на комплексной Z-плоскости

ПЗФ



9. Как преобразуются частоты аналогового и цифрового фильтров при билинейном преобразовании?
H(z) = H(p) при р = f(z); H(р) = H(z) при z = f –1 (p), где р и z – комплексные операторы преобразования Лапласа и Z-преобразования. Путем перехода к частоте с помощью замен р = j(), z = e jTд = e j находятся частотные преобразующие функции  = f(),  = f –1 (), устанавливающие связь между нормированными частотами аналогового  и цифрового  = Tд фильтров и их частотными характеристиками: H(j) = H(j) при  = f(); H(j) = H(j) при  = f –1 ()

Частоты аналогового фильтра  нормированы к частоте среза (с = 1), а частота цифрового фильтра  нормирована к частоте дискретизации fд:  = 2f/fд. Частотная характеристика цифрового фильтра определяется в диапазоне частот (0–fд/2), что соответствует изменению  в пределах (0–). При этом частота аналогового фильтра может принимать значения от 0 до , которые при билинейном преобразовании сжимаются в область частот (0– fд/2) (или (0–) – для ) цифрового фильтра






9. Чему равно требуемое число операций умножения на один отсчет сигнала при канонической форме его реализации?

---

Смотрите также файлы

• Формулировка задания.docx

• Удержания и вычеты из зарплаты.doc

• Мектепке дейінгі трбие мен оытуды, бастауыш, негізгі орта жне жалпы орта білімні жалпы білім беретін оу бадарламаларын, техникалы жне ксіптік, орта білімнен кейінгі,.docx

• Ты наш друг, русский язык!.doc

• Тест тапсырмаларыны банкі Абенбетова Айнур.docx