ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Дата:03.11.2022г.
Дисциплина: Математика
Тема урока:Интегральное исчисление
Обратная связь: Выполненные задания (фото) вы отправляете до 5.11.2022г. на адрес электронной почты: dinara_muldabaeva@mail.ru подписав документ: Фамилия, инициалы, номер группы (Иванов И.С. 230 группа) или в контакте Байназарова Динара.
Инструкция к уроку:
-
Запишите в тетрадьопорный конспект. -
Выполните задания (письменно), которые будут оценены отметкой.
Опорный конспект
Функция
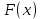 называется первообразной функции
называется первообразной функции 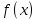 на некотором промежутке, если в каждой точке этого промежутка
на некотором промежутке, если в каждой точке этого промежутка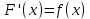
или, что тоже,
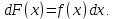
Например,
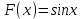 является первообразной для
является первообразной для 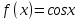 на всей числовой оси Ox, так как
на всей числовой оси Ox, так как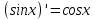 .
.Если функция
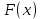 есть первообразная функции
есть первообразная функции 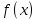 на
на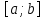 , то функция
, то функция 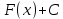 , где C – любое действительное число, также является первообразной для
, где C – любое действительное число, также является первообразной для 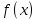 при любом значении C. Действительно,
при любом значении C. Действительно,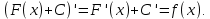
Пример 1. Найти первообразную функции
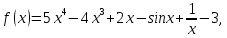
Решение.
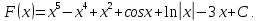
Если
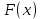 одна из первообразных функции
одна из первообразных функции 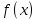 на
на 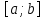 , то выражение
, то выражение 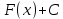
, где C произвольная постоянная, называется неопределенным интегралом функции
 и обозначается символом
и обозначается символом 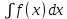 (читается: неопределенный интеграл
(читается: неопределенный интеграл  на
на 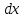 ). Итак,
). Итак,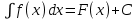 ,
,где
 называется подынтегральной функцией,
называется подынтегральной функцией, 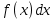 ‒ подынтегральным выражением,
‒ подынтегральным выражением, 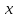 ‒ переменной интегрирования, а символ
‒ переменной интегрирования, а символ 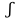 ‒ знаком неопределенного интеграла.
‒ знаком неопределенного интеграла.Свойства неопределенного интеграла
Из определения неопределенного интеграла следует, что:
-
Производная неопределенного интеграла равна подынтегральной функции:
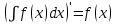
Действительно,
 и
и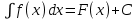 . Тогда
. Тогда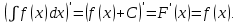
-
Дифференциал от неопределенного интеграла равен подынтегральному выражению
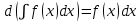
-
Неопределенный интеграл от производной равен самой функции плюс произвольная постоянная:
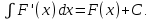
-
Неопределенный интеграл от дифференциала равен дифференцируемой функции плюс произвольная постоянная:
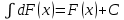 .
.5. Постоянный множитель k
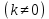 можно выносить за знак неопределенного интеграла:
можно выносить за знак неопределенного интеграла: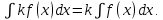
6. Неопределенный интеграл от алгебраической суммы конечного числа функции равен алгебраической сумме интегралов от этих функций:
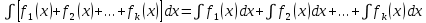 .
.Таблица неопределенных интегралов
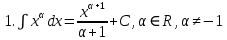 | 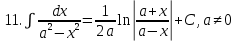 |
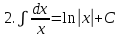 | 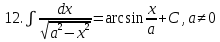 |
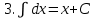 | 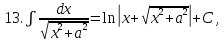 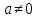 |
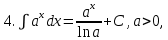 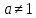 | 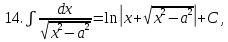 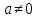 |
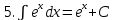 | 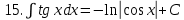 |
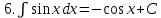 | 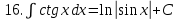 |
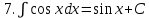 | 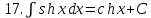 |
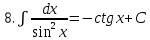 | 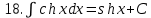 |
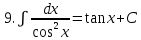 | 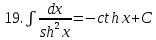 |
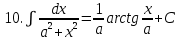 | 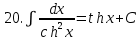 . . |
Методы интегрирования
1. Непосредственное (табличное) интегрирование.
Непосредственное (табличное) интегрирование ‒ это приведение интеграла к табличному виду с помощью основных свойств и формул элементарной математики.
Пример 2.
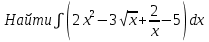 .
.Решение.
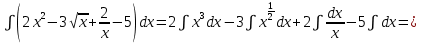
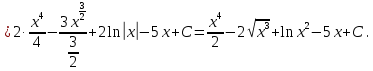
2. Метод замены переменной
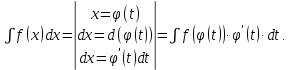
Пример 3.
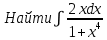 .
.Решение.
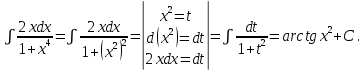
3.Метод интегрирования по частям
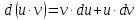
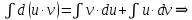
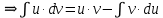 – формула интегрирования по частям.
– формула интегрирования по частям.По этой формуле берутся следующие типы интегралов:
1 тип
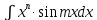
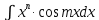
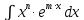
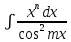
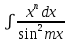
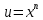 , формула применяется n раз, остальное dv.
, формула применяется n раз, остальное dv.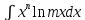
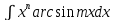
2 тип
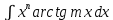
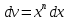 , формула применяется один раз.
, формула применяется один раз.Пример 4. Найти
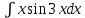
Решение.
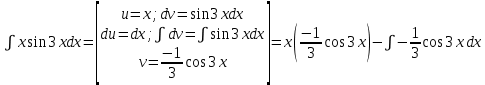
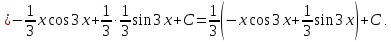
Определенный интеграл и его свойства. Формула Ньютона – Лейбница
Пусть в интеграле
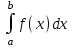
нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
Обозначим
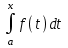 =F(х). Найдем производную функции F(х) по переменному верхнему пределу х.
=F(х). Найдем производную функции F(х) по переменному верхнему пределу х.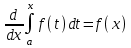
Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая-либо первообразная от непрерывной функции f(x), то
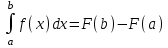
это выражение известно под названием формулы Ньютона – Лейбница.
Иногда применяют обозначение F(b) – F(a) = F(x)
 .
.Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Пример 13.Вычислить определенный интеграл:
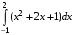 .
.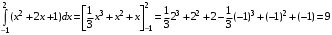 .
.Пример 14.Вычислить определенный интеграл:
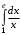 .
.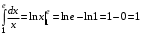 .
.Пример 15.Вычислить определенный интеграл:
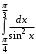 .
.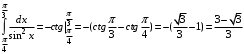 .
.Пример 16.Вычислить определенный интеграл:
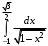 .
.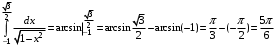 .
.Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования.