IDEF0 часто используется как способ исследования и проектирования систем на логическом уровне. Результаты анализа с помощью IDEF0 могут применяться при проектировании с использованием IDEF0 и DFD.IDEF0 определяет два графических объекта:

1. 
   Блок, с помощью которого обозначается некоторая функция (действия);
   
2. 
   Стрелка, с помощью которой указываются информационные или материальные объекты.
   

Модель IDEF0 представляет собой набор взаимоувязанных диаграмм. Каждая диаграмма является описанием системы или ее отдельных функциональных блоков в рамках некоторого уровня детализации.Контекстная диаграмма (КД)- диаграмма самого верхнего уровня иерархии, дает общее представление о системе. На КД отображается только один функциональный блок (контекстная функция).Далее контекстная функция декомпозируется на основные функции системы с помощью отдельной диаграммы. В свою очередь, каждая такая функция может быть разложена на более мелкие и т.д. При построении модели нужно соотнести каждый функциональный блок более низкого уровня с функциональным блоком более высокого уровня.Надо помнить, что некоторый функциональный блок и диаграмма его декомпозиции суть одно и того же, но рассматриваемое с разной степенью детализации. Отсюда следует, что все стрелки, связанные с рассматриваемым функциональным блоком, должны присутствовать на декомпозирующей его диаграмме (если таковая имеется). Исключения из этого правила возможны только в случае использования механизма туннелирования.Программные продукты, реализующие методологию IDEF0:

• 
  Business Studio
  
• 
  BPwin (AllFusion Process Modeller)
  
• 
  IDEF0.EM Tool
  
• 
  Design/IDEF 3.5
  
• 
  Ramus
  
• 
  MS Visio
  

В дальнейшем мы будем использовать BPwin в качестве CASE- средства.

2. 
   Диаграмма бизнес-процесса из BPWIN
   

Функциональная модель процесса состоит из 5 диаграмм:

• 
  Контекстная диаграмма;
  
• 
  Диаграмма второго уровня-декомпозиция контекстной диаграммы;
  
• 
  Диаграмма третьего уровня- декомпозиция блока ‘прием товара’;
  
• 
  Диаграмма четвертого уровня- декомпозиция блока ‘занесение товара в БД’;
  
• 
  Диаграмма пятого уровня- декомпозиция блока ‘занесения данных’;
  
• 
  Дерево диаграмм;
  

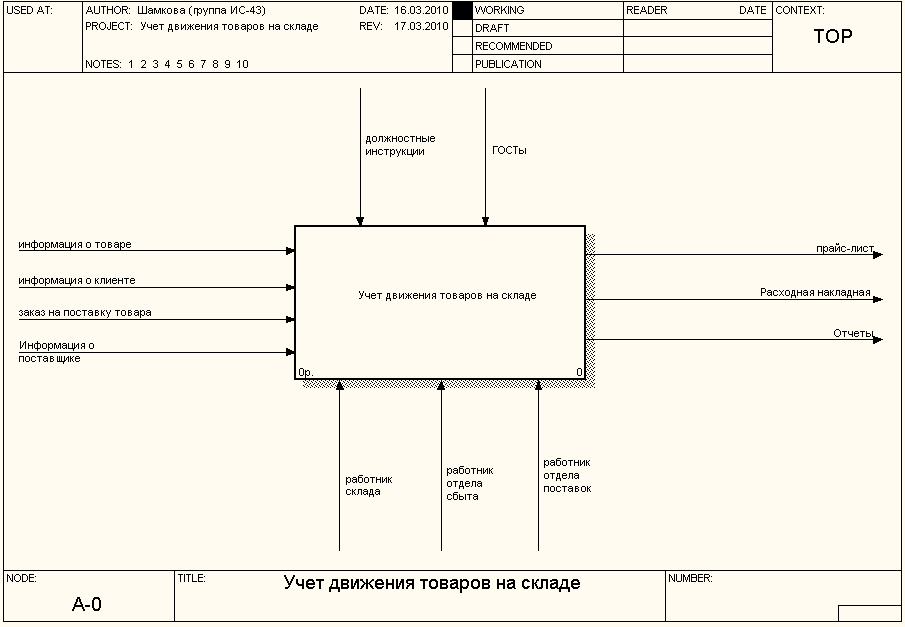
Рис1. Контекстная диаграмма.

---

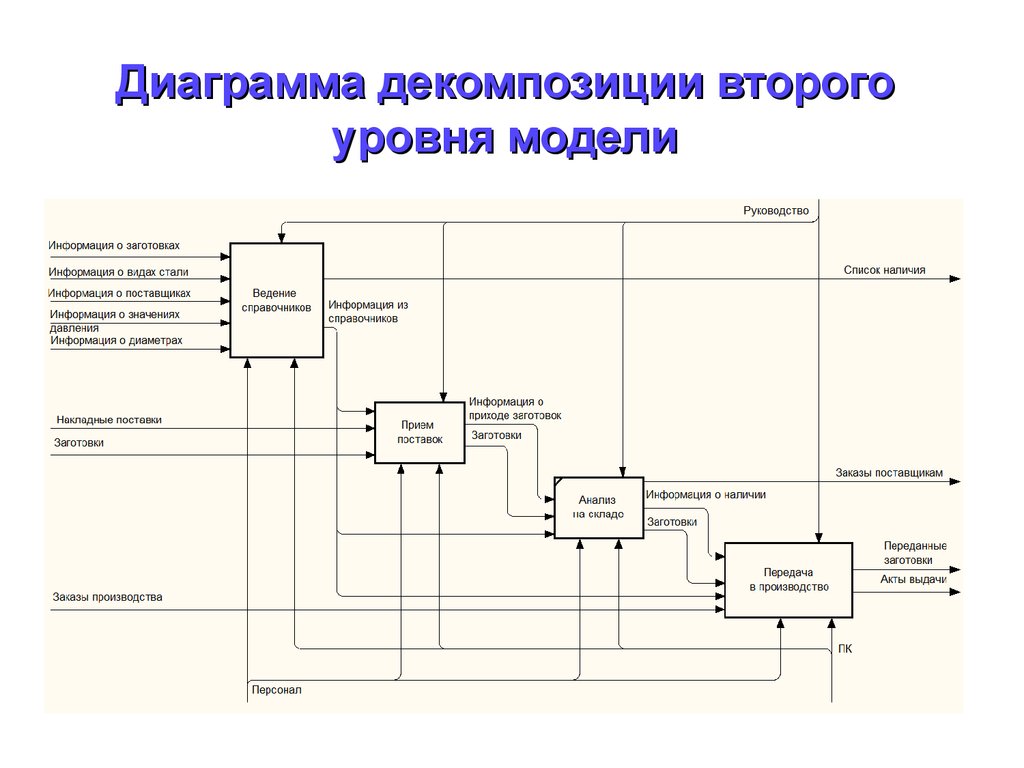
Рис2. Диаграмма второго уровня-декомпозиция контекстной диаграммы.



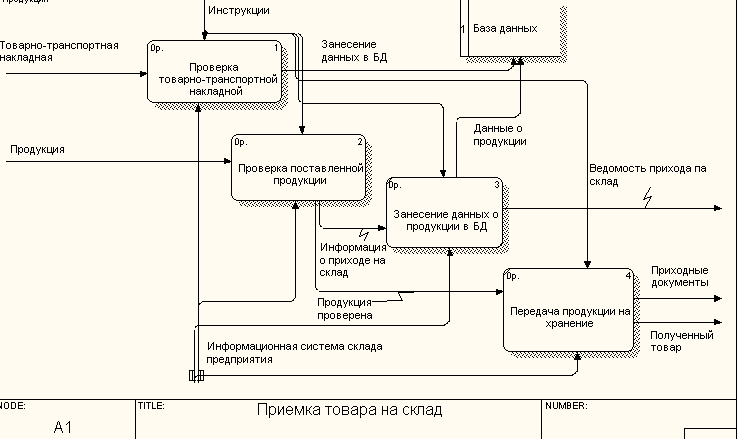
Рис3. Диаграмма третьего уровня-декомпозиция блока ‘прием товара’.



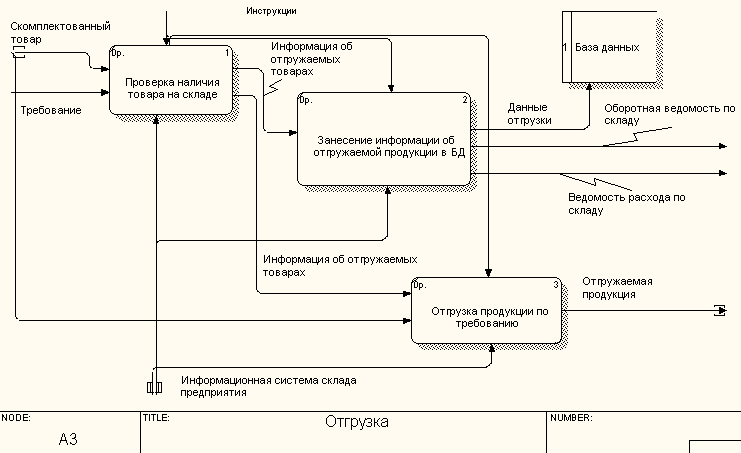
Рис4.Диаграмма четвертого уровня-декомпозиция блока ‘занесение товара в БД’.



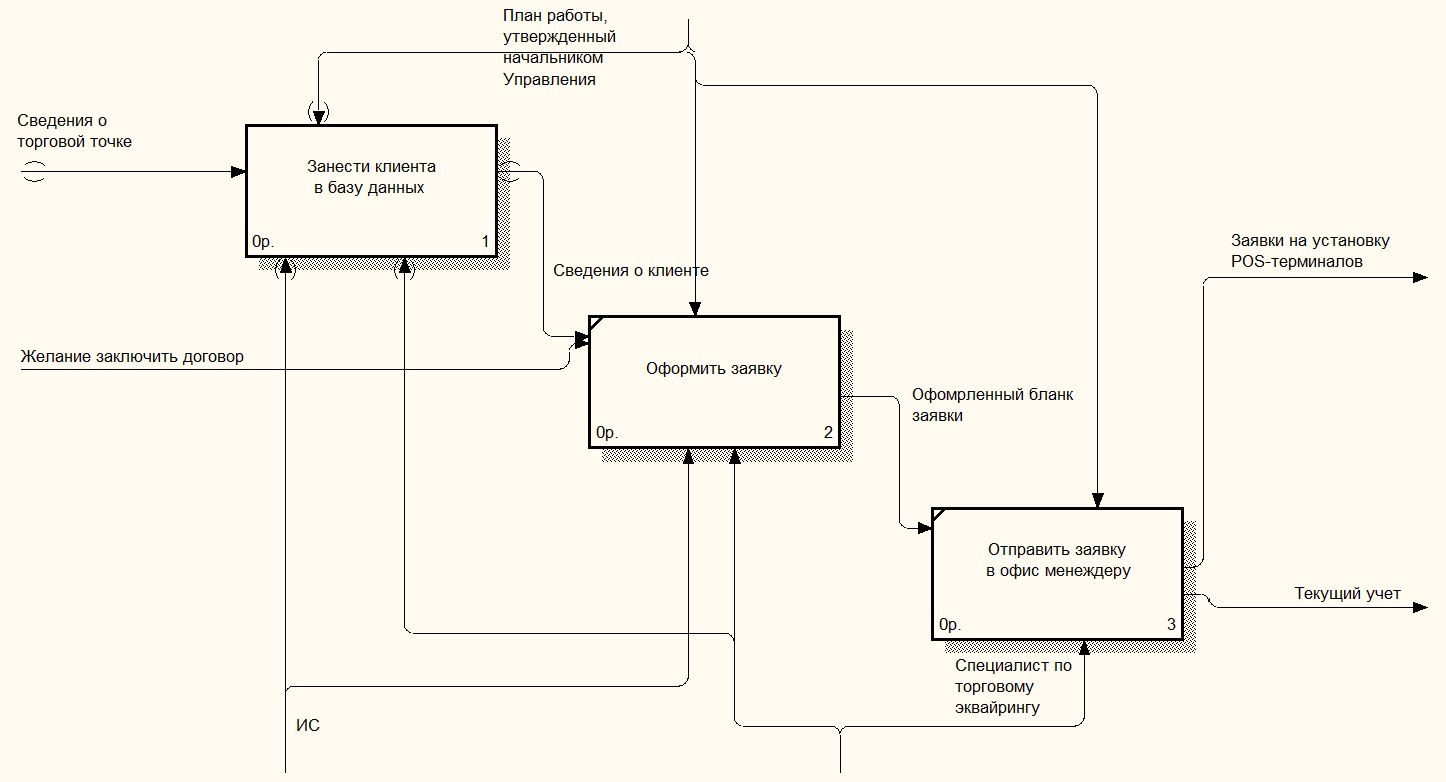
Рис5. Диаграмма пятого уровня-декомпозиция блока ‘занесение данных’.



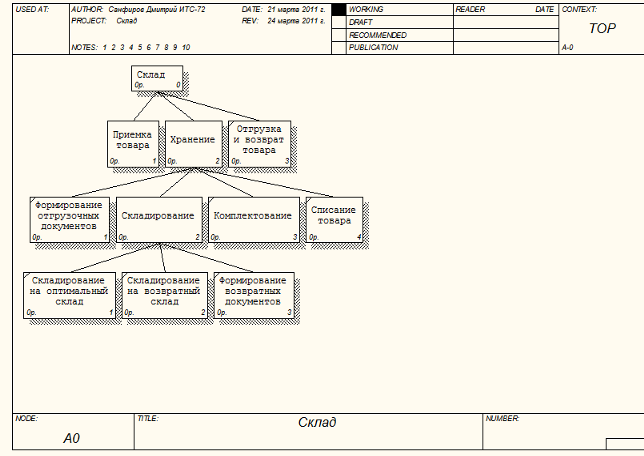
Рис6. Диаграмма дерева узлов.

2. 
   Расчет оценки функциональной модели.
   

1. 
   Вырожденная модель:
   

Вырожденная ФМ- дерево узлов представляется (вырождается) в виде цепи.a)Количественный метод оценки ФМ:

• 
  Количество уровней дерева:
  

R=5

• 
  Количество диаграмм на уровнях:
  

S1=1;s2=1;s3=1;s4=1;s5=1;

• 
  Количество функциональных блоков в j-й диаграмме на i-м уровне (nij);
  

N11=1;n12=1;n13=1;n14=1;n15=1;

• 
  Число стрелок у каждого блока:
  

A1=4;a2=4;a3=4;a4=4;a5=4;2)Минимальная модель:Минимальная ФМ- дерево узлов представляет собой урезанное бинарное дерево.a)Количественный метод оценки ФМ:

• 
  Количество уровней дерева:
  

r=5

• 
  Количество диаграмм на уровнях:
  

S1=1;s2=1;s3=1;s4=1;s5=1;

• 
  Количество функциональных блоков в j=й диаграмме на i-м уровне(nij):
  

N11=1;n12=2;n13=2;n14=2;n15=2;

• 
  Число стрелок у каждого блока:
  

A1=4;a2=4;a3=4;a4=4;a5=4;a6=4;a7=4;a8=4;a9=4;4)Регулярная модель:а)Количественный метод оценки ФМ:

• 
  Количество уровней дерева:
  

r=5

• 
  Количество диаграмм на уровнях:
  

S1=2;s2=1;s3=2;s4=4;s5=8;

• 
  Количество функциоанльных блоков в j-й диаграмме на i-м уровне(nij):
  

N11=1;n12=2;n13=4;n14=8;n15=16;

• 
  Число стрелок у каждого блока:
  

A1=4;a2=4;a3=4;a4=4;a5=4;a6=4;a7=4;a8=4;a9=4;a10=4;a11=4;a12=4;a13=4;a144;a15=4;a16=4;a17=4;a18=4;a19=4;20=4;a21=4a=;a22=4;a23=4;a24=4;a25=4;a26=4;a27=4;a28=4;a29=4;a30=4;a31=4;4) Наша модель:а) Количественный метод оценки ФМ:

• 
  Количество уровней дерева:
  

r=5

• 
  Количество диаграмм на уровнях:
  

S1=1;s2=1;s3=1;s4=1;s5=1;

• 
  Количество фунциональных блоков в j-й диаграмме на i-м уровне(nij);
  

N11=1;n12=3;n13=2;n14=3;n15=3;

• 
  Число стрелок у каждого блока:
  

A1=8;a2=6;a3=4;a4=3;a5=6;a63;a7=5;a8=5;a9=4;a10=5;a11=5;a12=5;

---

Анализ используемых стрелок:ас-количество стрелок;ас=22k1-коэффициент связанности модели;аT-количество тунельных стрелок;аT=2k2-коэффициент глубины проработки ФМВыводы по производному анализу:Коэффициент связанности k1, равный 0, 63, стремится k1, это говорит о том, что связанность в функциональной модели хорошая.Коэффициент глубины проработки k2, равный 0, 09, не стремится у 0, но и не стремится k1. Это говорит о средней глубине проработки функциональной модели. Такой результат получился ввиду небольшого количества «тунельных» стрелок по сравнению с обыкновенными стрелками ФМ.

---

Смотрите также файлы

• Подготовка к проверочной работе по теме Глагол.docx

• Человек и информация.docx

• Управление денежными потоками организации.docx

• .docx

• Учебника Тема урока Тип урока.doc