Задание 2

Выполнить синтез планетарного механизма 1-го типа (рис. 1) и определить общее передаточное отношение 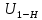графоаналитическим методом при следующих исходных данных:требуемое передаточное отношение 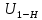= 4,2; число зубьев колеса 1 z₁ = 20 ; количество сателлитов k = 3.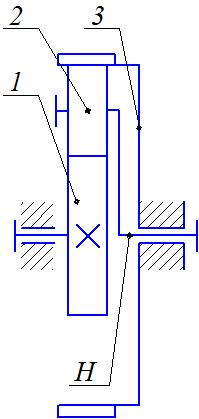



Рис. 1. Схема планетарного механизма

1 - центральное подвижное колесо; 2- сателлит; 3 – центральное подвижное колесо; H - водило.

Решение

Планетарный механизм можно отнести к типу зубчато-рычажных. Его структуру составляют подвижные зубчатые колёса 1, 2, неподвижное зубчатое колесо 3 и водило H, которое является звеном рычажного типа. Колесо 1 и водило H совершают вращательное движение, колесо 2 (сателлит) совершает плоское движение.

1) Определение неизвестного числа зубьев

Прямое передаточное отношение планетарного механизма 1-го типа определяется с помощью формулы:

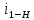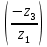= 1 - = 1 +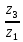

Условие соосности планетарного механизма 1-го типа выглядит так:

z₃= z₁ + 2·z₂

Тогда выражение для вычисления прямого передаточного отношения можно записать в виде:

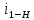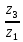= 1 + = 1 + 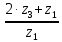=1 + 2∙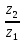

или 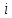= 1 + 2∙ 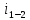, откуда 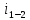= 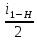– 1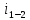

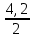= – 1 = 1,1

Расчётное число зубьев колеса 2 (сателлитного колеса)

---

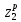= 20∙1,1 =22

Принимаем z₂ = 22

Из условия соосности определяем число зубьев центрального неподвижного колеса

z₃= z₁ + 2·z₂ = 20 + 2·22 = 64

Таким образом, для проектируемого механизма числа зубьев колёс z₁ = 20; z₂ = 22; z₃ = 64.

2) Поверка принятых чисел зубьев по условиям собираемости и соседства

Условие собираемости для механизма 1-го типа выглядит так

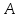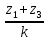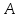= , - целое число

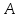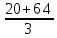= = 28

В результате расчётов получилось целое значение, значит условие собираемости выполнено.

Проверяем условие соседства

sin >
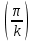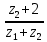
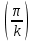sin = sin 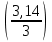= 0,866

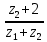= = 0,57
0,866 > 0,57

Значит условие соседства выполнено

Определение фактического значения прямого передаточного отношения

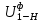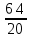= 1 + = 1 + = 4,2
∆U = 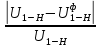·100% = 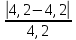·100% = 0 %

Фактическое значение передаточного отношения отличается от его заданного значения на 0,6 %, что допустимо.

Таким образом, числа зубьев спроектированного планетарного механизма

---

z₁ = 20, z₂ = 22, z₃ = 64 удовлетворяют условиям синтеза и обеспечивают заданное передаточное отношение в пределах требуемой точности.

---

Смотрите также файлы

• Подраздел А. Н. Островский. Снегурочка.doc

• Влияние устного народного творчества на развитие речи детей 34 лет.docx

• Методические рекомендации по выполнению внеаудиторных самостоятельных работ по учебной дисциплине мдк 02. 01 Технология публикации цифровой мультимедийной информации.doc

• Памятка для Авиационного персонала по гигиене зрения.pdf

• Какие особенности характерны для строения и функции тонкого кишечника человека.docx