Файл: Реферат по дисциплине "математика" "Применение производной в науке и технике".docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 07.12.2023

Просмотров: 315

Скачиваний: 10

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФГОУ СПОНовосибирский аграрный колледжРеферат по дисциплине "математика""Применение производной в науке и технике"С. Раздольное 2008 г.СодержаниеВведение

  1. Теоретическая часть
1.1 Задачи, приводящие к понятию производной1.2 Определение производной1.3 Общее правило нахождения производной1.4 Геометрический смысл производной1.5 Механический смысл производной1.6 Производная второго порядка и её механический смысл1.7 Определение и геометрический смысл дифференциала2. Исследование функций с помощью производнойЗаключениеЛитератураВведениеВ первой главе моего реферата речь пойдёт о понятии производной, правилах её применения, о геометрическом и физическом смысле производной. Во второй главе моего реферата речь пойдёт о применении производной в науке и технике и о решении задач в этой области.

  1. Теоретическая часть
1.1 Задачи, приводящие к понятию производнойПри изучении тех или иных процессов и явлений часто возникает задача определения скорости этих процессов. Её решение приводит к понятию производной, являющемуся основным понятием дифференциального исчисления.Метод дифференциального исчисления был создан в XVII и XVIII вв. С возникновением этого метода связаны имена двух великих математиков – И. Ньютона и Г.В. Лейбница.Ньютон пришёл к открытию дифференциального исчисления при решении задач о скорости движения материальной точки в данный момент времени (мгновенной скорости).Как известно, равномерным движением называют такое движение, при котором тело в равные промежутки времени проходит равные по длине отрезки пути. Путь, пройденный телом в единицу времени, называют скоростью равномерного движения.Однако чаще всего на практике мы имеем дело с неравномерным движением. Автомобиль, едущий по дороге

, замедляет движение у переходов и ускоряет его на тех участках, где путь свободен; самолёт снижает скорость при приземлении и т.д. Поэтому чаще всего нам приходится иметь дело с тем, что за равные отрезки времени тело проходит различные по длине отрезки пути. Такое движение называют неравномерным. Его скорость нельзя охарактеризовать одним числом.

Часто для характеристики неравномерного движения пользуются понятием средней скорости движения за время ∆t٫ которое определяется соотношением где ∆s – путь, пройденный телом за время ∆t.

Так, при свободном падении тела средняя скорость его движения за первые две секунды есть

Практически такая характеристика движения, как средняя скорость, говорит о движении очень мало. Действительно, при 4,9 м/с, а за 2-ю – 14,7 м/с, в то время как средняя скорость за первые две секунды составляет 9,8 м/с. Средняя скорость в течение первых двух секунд не даёт никакого представления о том, как происходило движение: когда тело двигалось быстрее, а когда медленнее. Если же задать средние скорости движения для каждой секунды в отдельности, то мы будем знать, например, что во 2-ю секунду тело двигалось значительно быстрее, чем в 1-ю. Однако в большинстве случаев значительно быстрее, чем нас мало устраивает. Ведь нетрудно понять, что в течение этой 2-й секунды тело также движется по-разному: в начале медленнее, в конце быстрее. А как оно движется где-то в середине этой 2-й секунды? Иными словами, как определить мгновенную скорость?

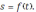
Пусть движение тела описывается законом 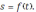Рассмотрим путь, пройденный телом за время от t0 до t0 + ∆t, т.е. за время, равное ∆t. В момент t0 телом пройден путь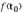 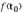, в момент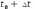 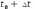– путь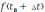 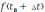. Поэтому за время ∆t тело прошло путь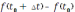

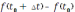
и средняя скорость движения тела за этот промежуток времени составит.

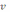
Чем меньше промежуток времени ∆t, тем точнее можно установить, с какой скоростью движется тело в момент t0, так как движущееся тело не может значительно изменить скорость за малый промежуток времени. Поэтому средняя скорость при стремлении ∆t к нулю приближается к действительной скорости движения и в пределе даёт скорость движения 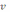в данный момент времени t0 (мгновенную скорость).

Таким образом,


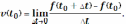
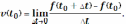
Определение 1. Мгновенная скорость прямолинейного движения тела в данный момент времени t0 называется предел средней скорости за время от t0 до t0 + ∆t, когда промежуток времени ∆t стремится к нулю.

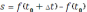
Итак, чтобы найти скорость прямолинейного неравномерного движения в данный момент, нужно найти предел отношения приращения пути ∆ 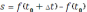к приращению времени ∆t при условии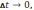 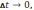т.е. Лейбниц пришёл к открытию дифференциального исчисления при решении задачи о построении касательной к любой кривой, заданной своим уравнением.

Решение этой задачи имеет большое значение. Ведь скорость движущейся точки направлена по касательной к её траектории, поэтому определение скорости снаряда на его траектории, скорости любой планеты на её орбите сводится, к определению направления касательной к кривой.

Определение касательной как прямой, имеющей с кривой только одну общую точку, справедливое для окружности, непригодно для многих других кривых.

Ниже представленное определение касательной к кривой, не только соответствует интуитивному представлению о ней, но и позволяет фактически находить её направление, т.е. вычислять угловой коэффициент касательной.

Определение 2. Касательной к кривой в точке М называется прямая МТ, которая является предельным положением секущей ММ1, когда точка М1, перемещаясь по кривой, неограниченно приближается к точке М.
1.2 Определение производной

Заметим, что при определении касательной к кривой и мгновенной скорости неравномерного движения, по существу, выполняются одни и те же математические операции:

  1. Заданному значению аргумента дают приращение и вычисляют новое значение функции, соответствующее новому значению аргумента.

  2. Определяют приращение функции, соответствующее выбранному приращению аргумента.

  3. Приращение функции делят на приращение аргумента.

  4. Вычисляют предел этого отношения при условии, что приращение аргумента стремится к нулю.
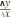
К предельным переходам такого типа приводят решения многих задач. Возникают необходимость сделать обобщение и дать название этому предельному переходу.Скорость изменения функции в зависимости от изменения аргумента можно, очевидно, охарактеризовать отношением 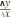. Это отношение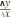 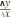называется средней скоростью изменения функции на отрезке от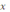 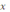до 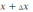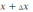. Сейчас нужно рассмотреть предел дроби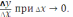 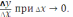Предел этого отношения при стремлении приращения аргумента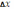 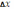к нулю (если этот предел существует) представляет собой некоторую новую функцию от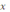 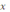. Эту функцию обозначают символами y’,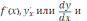 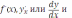называют производной данной функции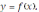 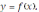так как она получена (произведена) из функции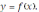 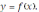Сама же функция
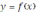
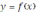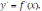
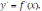
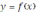
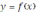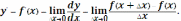
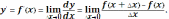
называется первообразной функцией по отношению к своей производной Определение 3. Производной функции в данной точке называют предел отношения приращения функции ∆y к соответствующему приращению аргумента ∆x при условии, что ∆x→0, т.е. 1.3 Общее правило нахождения производнойОперацию отыскания производной некоторой функции называют дифференцированием функции, а раздел математики, изучающий свойства этой операции, – дифференциальным исчислением.Если функция имеет производную в точке x=a, то говорят, что она дифференцируема в этой точке. Если функция имеет производную в каждой точке данного промежутка, то говорят, что она дифференцируема на этом промежутке.Определение производной не только с исчерпывающей полнотой характеризует понятие скорости изменения функции при изменении аргумента, но и даёт способ фактического вычисления производной данной функции. Для этого необходимо выполнить следующие четыре действия (четыре шага), указанные в самом определении производной:

  1. Находят новое значение функции, представив в данную функцию вместо x новое значение аргумента : .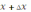

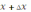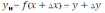
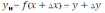  2. Определяют приращение функции, вычитывая данное значение функции из её нового значения: .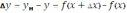

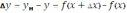  3. Составляют отношение приращения функции к приращению аргумента: .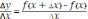

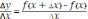  4. Переходят к пределу при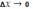 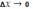и находят производную: .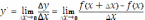

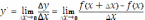Смотрите также файлы