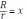
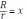. Тогда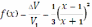 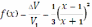. Отсюда видно, что относительная погрешность не зависит от длины бревна, а определяется отношением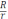 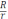. Поскольку при 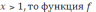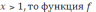возрастает на промежутке [1; 2]. Поэтому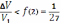 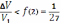, а значит, относительная погрешность не превосходит 3,7%. В практике лесоведения такая погрешность считается вполне допустимой. С большей точностью практически невозможно измерить ни диаметры торцов (ведь они несколько отличаются от кругов), ни длину бревна, поскольку измеряют не высоту, а образующую конуса (длина бревна в десятки раз больше диаметра, и это не приводит к большим погрешностям). Таким образом, на первый взгляд неправильная, но более простая формула для объёма усечённого конуса в реальной ситуации оказывается вполне правомерной. Многократно проводившиеся с помощью специальных методов проверки показали, что при массовом учёте делового леса относительная погрешность при использовании рассматриваемой формулы не превосходит 4%.

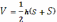
Задача №2. При определении объёмов ям, траншей вёдер и других ёмкостей, имеющих форму усечённого конуса, в с/х практике иногда пользуются упрощённой формулой 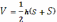, где – высота, 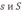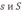– площади оснований конуса. Выясните, завышается или занижается при этом реальный объём, оцените относительную погрешность при естественном для практики условии:

---

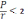
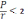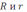
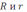( – радиусы оснований, .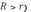

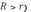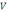
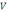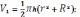
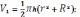
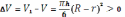
Решение. Обозначив через истинное значение объёма усечённого конуса, а через значение, вычисленное по упрощённой формуле, получим: 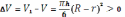, т.е.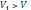 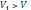. Значит, упрощённая формула даёт завышение величины объёма. Повторив далее решение предыдущей задачи, найдём, что относительная погрешность будет не больше 6,7%. Вероятно, такая точность допустима при нормировании землеройных работ – ведь ямы не будут идеальными конусами, да и соответствующие параметры в реальных условиях замеряют весьма грубо.

Задача №3. В специальной литературе для определения угла β поворота шпинделя фрезерного станка при фрезеровании муфт с зубьями выводится формула 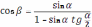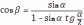, где 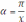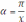. Так как эта формула сложна, то рекомендуется отбросить её знаменатель и пользоваться упрощённой формулой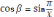 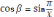. При каких (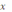

---

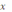– целое число, 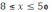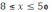) можно пользоваться этой формулой, если при определении угла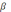 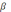допускается погрешность в ?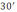

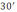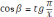
Решение. Точную формулу после несложных тождественных преобразований можно привести к виду 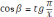. Поэтому при использовании приближённой формулы допускается абсолютная погрешность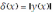 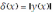, где 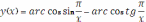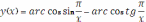. Исследуем функцию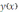 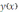на отрезке [8; 50]. При этом 0,06, т.е. угол принадлежит первой четверти. Имеем: 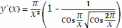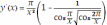. Заметим, что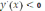 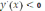на рассматриваемом промежутке, а значит, функция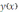 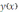на этом промежутке убывает. Поскольку далее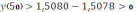 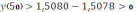, то 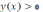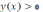при всех рассматриваемых . Значит, 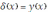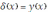. Так как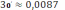

---

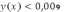
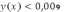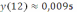
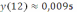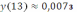
радиан, то достаточно решить неравенство . Решая это неравенство подбором, находим, что , 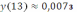. В силу того, что функция убывает, следует, что .

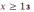
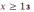Заключение
Применение производной довольно широко, и его можно полностью охватить в работе такого типа, однако я попытался раскрыть основные базовые моменты. В наше время, в связь с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальными в решении как простых, так и сверхсложных задач.

Литература

1. 
   В.А. Петров «Математический анализ в производственных задачках»
   
2. 
   Соловейчик И.Л., Лисичкин В.Т. «Математика»
   

---

Смотрите также файлы

• Модуль зубьев.docx

• Статья 357 ук рф.docx

• Роль социальной рекламы в современном обществе.docx

• Зачёт по политологии.rtf

• Тест по электронной цифровой подписи Какие функции выполняет эцп.docx