Вообще говоря, производная – это «новая» функция, произведённая от данной функции по указанному правилу.
1.4 Геометрический смысл производной
Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, состоит в следующем: значение производной функции в точке x равно угловому коэффициенту касательной, проведённой к графику функции в той же точке x, т.е.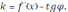

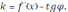
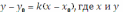
Уравнение касательной, как всякой прямой, проходящей через данную точку в данном направлении, имеет вид 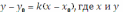– текущие координаты. Но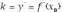 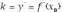и уравнение касательной запишется так: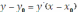 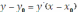. Уравнение нормали запишется в виде .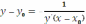
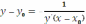1.5 Механический смысл производной
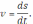
Механическое истолкование производной было впервые дано И. Ньютоном. Оно заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е. 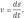Таким образом, если закон движения материальной точки задан уравнением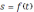 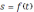, то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени нужно найти производную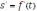 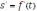и подставить в неё соответствующее значение t.
1.6 Производная второго порядка и её механический смысл
Получим (уравнение из проделанного в учебнике Лисичкин В.Т. Соловейчик И.Л. «математика» с. 240):

---

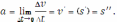
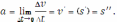
Таким образом, ускорение прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента. В этом и заключается механический смысл второй производной.
1.7 Определение и геометрический смысл дифференциала
Определение 4. Главная часть приращения функции, линейная относительно приращения функции, линейная относительно приращения независимой переменой, называется дифференциалом функции и обозначается знаком d, т.е. .

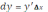
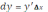Дифференциал функции геометрически изображается приращением ординаты касательной, проведённой в точке M (x; y) при данных значениях x и ∆x.

Вычисление дифференциала – .

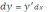
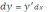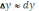
Применение дифференциала в приближённых вычислениях – 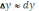, приближённое значение приращения функции совпадает с её дифференциалом.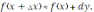

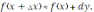
Теорема 1. Если дифференцируемая функция возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.

Теорема 2. Если производная функция положительна (отрицательна) в не котором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).

Сформулируем теперь правило нахождения интервалов монотонности функции

---

1. 
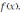
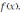
   Вычисляют производную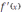 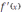данной функции.
   
2. 
   Находят точки, в которых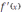 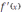равна нулю или не существует. Эти точки называются критическими для функции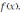
   
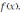
3. 
   Найденными точками область определения функции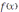 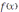разбивается на интервалы, на каждом из которых производная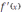 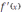сохраняет свой знак. Эти интервалы являются интервалами монотонности.
   
4. 
   Исследуют знак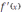 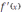на каждом из найденных интервалов. Если на рассматриваемом интервале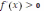 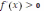, то на этом интервале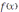 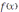возрастает; если же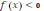 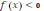, то на таком интервале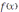 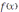убывает.
   

В зависимости от условий задачи правило нахождения интервалов монотонности может упрощаться.

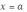
Определение 5. Точка 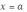называется точкой максимума (минимума) функции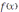 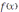, если имеет место неравенство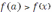 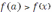соответственно

---

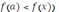
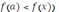для любого x из не которой окрестности точки .

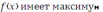
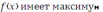Если – точка максимума (минимума) функции , то говорят, что (минимум) в точке . Максимум и минимум функции объединяют название экстремум функции, а точки максимума и минимума называют точками экстремума (экстремальными точками).

Теорема 3. (необходимый признак экстремума). Если является точкой экстремума функции и производная в этой точке существует, то она равна нулю: .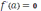

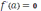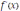
Теорема 4. (достаточный признак экстремума). Если производная 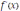при переходе x через a меняет знак, то a является точкой экстремума функции .

Основные моменты исследования производной:

1. 
   Находят производную .
   
2. 
   Находят все критические точки из области определения функции.
   
3. 
   Устанавливают знаки производной функции при переходе через критические точки и выписывают точки экстремума.
   
4. 
   Вычисляют значения функции в каждой экстремальной точке.
   

---

2. 
   Исследование функций с помощью производной
   

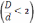
Задача №1. Объём бревна. Круглым деловым лесом называют брёвна правильной формы без дефектов древесины с относительно небольшой разницей 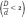диаметров толстого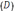 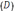и тонкого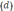 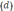концов. При определении объёмов круглого делового леса обычно применяют упрощённую формулу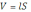 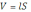, где 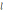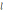– длина бревна,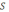 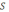– площадь его среднего сечения. Выясните, завершается или занижается при этом реальный объём; оцените относительную погрешность.

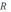
Решение. Форма круглого делового леса близка к усечённому конусу. Пусть 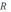– радиус большего,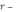 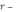меньшего конца бревна. Тогда его почти точный объём (объём усеченного конуса) можно, как известно, найти по формуле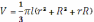 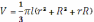. Пусть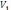 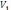– значение объёма, вычисленное по упрощённой формуле. Тогда ;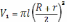

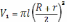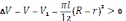
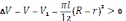, т.е.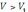 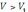. Значит, упрощённая формула даёт занижение величины объёма. Положим теперь

---

Смотрите также файлы

• Модуль зубьев.docx

• Статья 357 ук рф.docx

• Роль социальной рекламы в современном обществе.docx

• Зачёт по политологии.rtf

• Тест по электронной цифровой подписи Какие функции выполняет эцп.docx