Файл: Контрольная работа по дисциплине Математика Зарипова Л. С. Помощь студентам.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 22
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Министерство науки и ВЫСШЕГО ОБРАЗОВАНИЯ Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Уральский государственный экономический университет» (УрГЭУ) |
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Математика»
Зарипова Л.С. Помощь студентам. Автор.
Ват сап. +79538233004
| Институт непрерывного и дистанционного образования Направление подготовки ______________________ Направленность (профиль) __________________________________ Кафедра __________________________________ Дата защиты: ________________ Оценка: ________________ | | Студент ___________________________ Группа ____________________ Руководитель ___________________________ __________________ (ФИО, должность, звание) |
Екатеринбург
2019 г.
2. Решение:
Для решения вычисления определителя приведем матрицу к верхнетреугольному виду, используя элементарные преобразования над строками матрицы и свойства определителя матрицы.
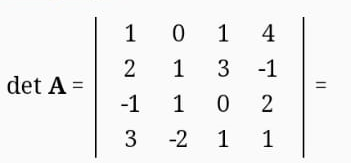
От 2 строки отнимаем 1 строку, умноженную на 2; к 3 строке добавляем 1 строку, умноженную на 1; от 4 строки отнимаем 1 строку. умноженную на 3.
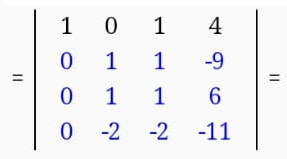
От 3 строки отнимаем 2 строку, умноженную на 1; к 4 строке добавляем 2 строку, умноженную на 2.
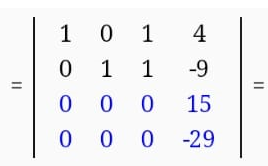
К четвертой строке добавляем 3 строку, умноженную на 29/15
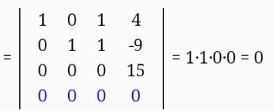
3. Решение:
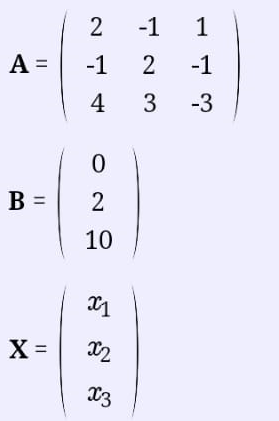
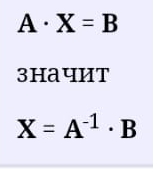
Найдем обратную матрицу методом алгебраических дополнений.
Найдем детерминант матрицы А:
Определитель матрицы А отличен от нуля. Следовательно, обратная матрица А-1 существует. Для вычисления обратной матрицы найдем дополнительные миноры и алгебраические дополнения матрицы А.
Найдем минор М11 и алгебраическое дополнение А11 . В матрице А вычеркиваем строку 1 и столбец 1.

Ниже покажем детальное вычисление определителя матрицы.
Найдем минор М12 и алгебраическое дополнение А12. В матрице А вычеркиваем строку 1 и столбец 2.

Найдем минор М13 и алгебраическое дополнение А13. В матрице А вычеркиваем строку и столбец 3.

Найдем минор М21 и алгебраическое дополнение А21. В матрице А вычеркиваем строку 2 и столбец 1.

Найдем минор М22 и алгебраическое дополнение А22. В матрице А вычеркиваем строку 2 и столбец 2.

Найдем минор М23 и алгебраическое дополнение А23. В матрице А вычеркиваем строку 2 и столбец 3.

Найдем минор М31 и алгебраическое дополнение А31. В матрице А вычеркиваем строку 3 и столбец 1.

Найдем минор М 32 и алгебраическое дополнение А32. В матрице А вычеркиваем строку 3 и столбец 2.

Найдем минор М33 и алгебраическое дополнение А33. В матрице А вычеркиваем строку 3 и столбец 3.

Выпишем союзную матрицу (матрицу алгебраических дополнений):

Транспонированная союзная матрица:

Найдем обратную матрицу:

Найдем решение:
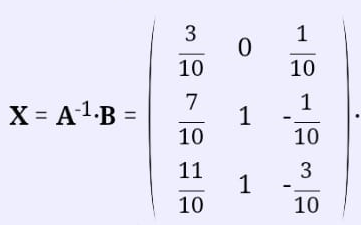
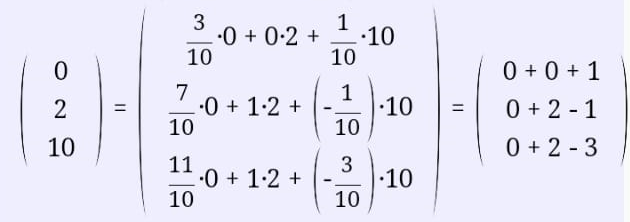
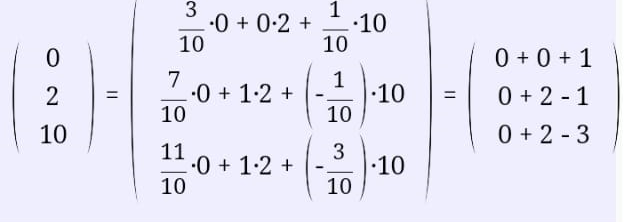
Ответ:
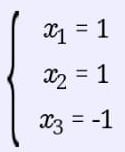
Решение:
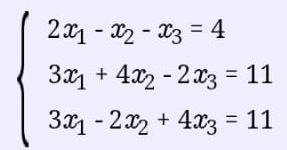
Перепишем систему уравнений в матричном виде и решим его методом Гаусса.

1ю строку делим на 2

От 2 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 3.
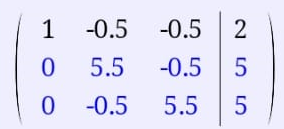
2 – ю строку делим на 5,5:
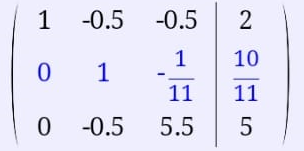
К 1 строке добавляем 2 строку, умноженную на 0,55; к 3 строке добавляем 2 строку, умноженную на 0,5.
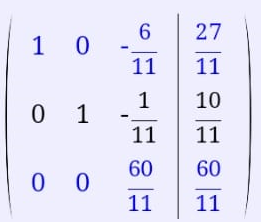
3ю строку делим на 60/11.
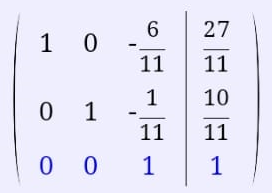
К 1 строке добавляем 3 строку, умноженную на 6/11; к 2 строке добавляем 3 строку, умноженную на 1/11.
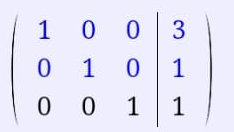
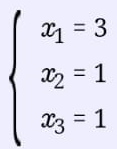
Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:
2*3-1-1=61-1=4
3*3+4*1-2*1=9+4-2=11
3*3-2*1+4*1=9-2+4=11
Проверка выполнена успешно.