Практическое задание 2

Тема 4. Определение синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике

Тема 5. Тригонометрические функции произвольного угла, их свойства и элементарные тригонометрические тождестваФормулировка задания: решить один вариант предложенной проверочной работы 2 в соответствии с первой буквой вашей фамилии (бланк выполнения задания).Проверочная работа 2Вариант 1

1. 
   B ∆ABC ےC = 90◦, CH – высота, BC = 4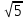 , BH = 4. Найдите tg A.
   

Углы A и BCH равны как углы со взаимно перпендикулярными сторонами. Следовательно,tgA = BH/CHНайдем длину стороны CH из прямоугольного треугольника BCH по теореме Пифагора, получим:CH^2 = BC^2 -BH^2CH = 4*2=8Получаем:tgA = BH/CHtgA = 4/8=0.50Ответ: 0,5.2. Найдите значение выражения: 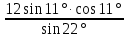=63. Найдите значение выражения:−4 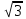cos(−750◦)=−4.624. Найдите: 24 cos2α, если sinα = −0,2.cos2α = cos²α - sin²α = 1 - sin²α - sin²α = 1- 2sin²α24cos2α = 24·( 1 - 2sin²α) = 24 - 48·sin²α = 24 - 48·(-0.2)² = 24 - 48·0.04 =24 - 1.92 = 22.085. Найдите: 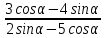, если tgα = 3.42/2^log2 3 =4*3 = 126. Основания равнобедренной трапеции равны 51 см и 65 см. Боковые стороны равны 25 см. Найдите синус острого угла трапеции.Пусть CE — высотаEB=(AB-DC)/2 = 7По теореме Пифагора находим: CE=√CB^2 -EB^2 = 24ТогдаSin B= CE/CBC=0.967. Известно, что cosα = 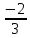, 8 < α < 9. Вычислите значения остальных тригонометрических функций угла α.Sinα= √5/3Tanα =√5/2ctg α =2/√58. Найдите область определения и область значения данной функции y = 2 + sinx.y' = cos(x)Приравниваем ее к нулю:cos(x) = 0x1 = 7.854x2 = 10.9969. Найдите значение функции f(x) = 2 − sin2x в точке x = 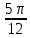.(2-sin(2·x))′=-2·cos(2·x)

---

(-sin(2·x))' = (-sin(2·x))'(2·x)' = -2·cos(2·x)(2·x)′=2-2·cos(2· )=1,710. Найдите период функции у = sin3x · cosx + cos3x · sinx.1. Находим интервалы возрастания и убывания. Первая производная.f'(x) = -4·sin(x)·sin(3·x)+4·cos(x)·cos(3·x)илиf'(x)=4·cos(4·x)Находим нули функции. cos(4·x) = 0Откуда:x1 = 0.39269908x2 = 3.5342917В окрестности точки x = 0.39269908 производная функции меняет знак с (+) на (-). Следовательно, точка x = 0.39269908 - точка максимума.

---

Смотрите также файлы

• Что такое разговоры о важном .docx

• Самостоятельная работа по модулю Алгебра.doc

• Проектирование учебного занятия на основании примерной рабочей.pdf

• Автор guru.docx

• Методические рекомендации по написанию, оформлению и защите.docx