Файл: Билеты для проведения муниципального публичного зачета по геометрии для обучающихся 8 класса Билет 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 519
Скачиваний: 32
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Билеты для проведения муниципального публичного зачета по геометрии для обучающихся 8 класса
Билет 1.
-
Определение многоугольника, вершины, стороны, диагонали и периметра многоугольника. Формула суммы углов выпуклого многоугольника.
Многоугольник – это геометрическая фигура, у которой смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
Вершина многоугольника – это точка пересечения двух соседних сторон многоугольника.
Сторона многоугольника – это отрезок соединяющий две соседние вершины многоугольника.
Диагональ многоугольника – это отрезок, соединяющий две любые не соседние вершины многоугольника.
Периметр многоугольника – это сумма длин всех сторон многоугольника.
| Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины. Сумма углов выпуклого n-угольника равна (n-2) ∙ 180 ̊ | 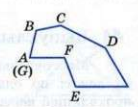 Рис.1 – Многоугольник |
2. Доказать теорему о средней линии треугольника.
Теорема
Средняя линия треугольника параллельна основанию и равна его половине
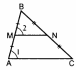 | Дано: ΔABC, MN – средняя линия Доказать: MN || AC, MN = 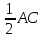 |
| Доказательство:
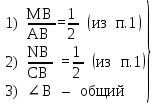 ⟹ MN = ⟹ MN = 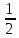 AC AC
| |
Билет 2.
-
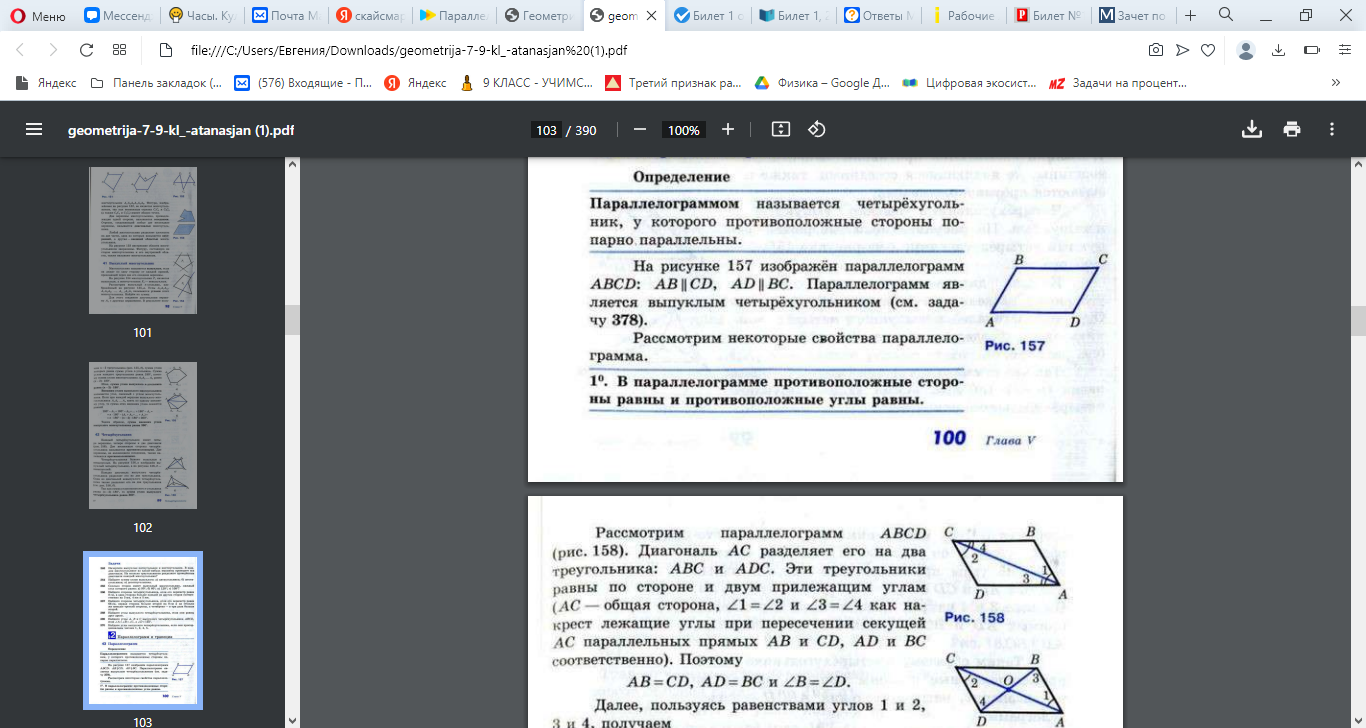
Дайте определение и свойства параллелограмма.
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны и равны.
Свойства параллелограмма
|  |
-
Докажите свойство медиан треугольника
Теорема
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.
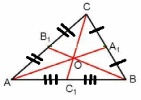 | Дано: ΔABC, AA1, BB1, CC1 — медианы Доказать: 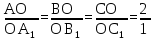 |
| Доказательство: 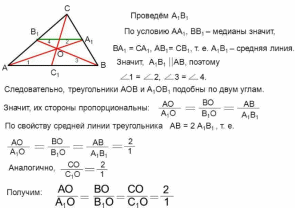 Что и требовалось доказать | |
Билет 3.
1. Дайте определение и назовите свойства прямоугольника.
Прямоугольник – это параллелограмм, у которого все углы прямые
Свойства прямоугольника (все от параллелограмма)
Особое свойство прямоугольника: Диагонали прямоугольника равны |  |
2. Докажите теорему Пифагора.
Теорема
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
b
а
А
b
а
с
с
 Дано:
Дано: b
с
∆АВС;
с
 С=90
С=90 ;
;В
С
b
а
а
с
АВ=с;
ВС=а;
b
а
АС=b;
Док-ть:
Доказательство:
-
Достроим треугольник до квадрата со стороной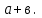
-
Площадь S этого квадрата равна S=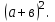
-
С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна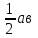 , и квадрата со стороной
, и квадрата со стороной 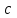 , поэтому
, поэтому
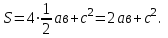
-
Таким образом,
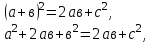
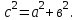
Что и требовалось доказать
Билет 4.
-
Дайте определение и назовите свойства ромба.
Ромб – это параллелограмм, которого все стороны равны.
Свойства ромба (все от параллелограмма)
Особые свойства ромба: 1. Диагонали ромба перпендикулярны. 2. Диагонали ромба являются биссектрисами его углов. 3. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4. (AC2 + BD2 = 4*AB2) | 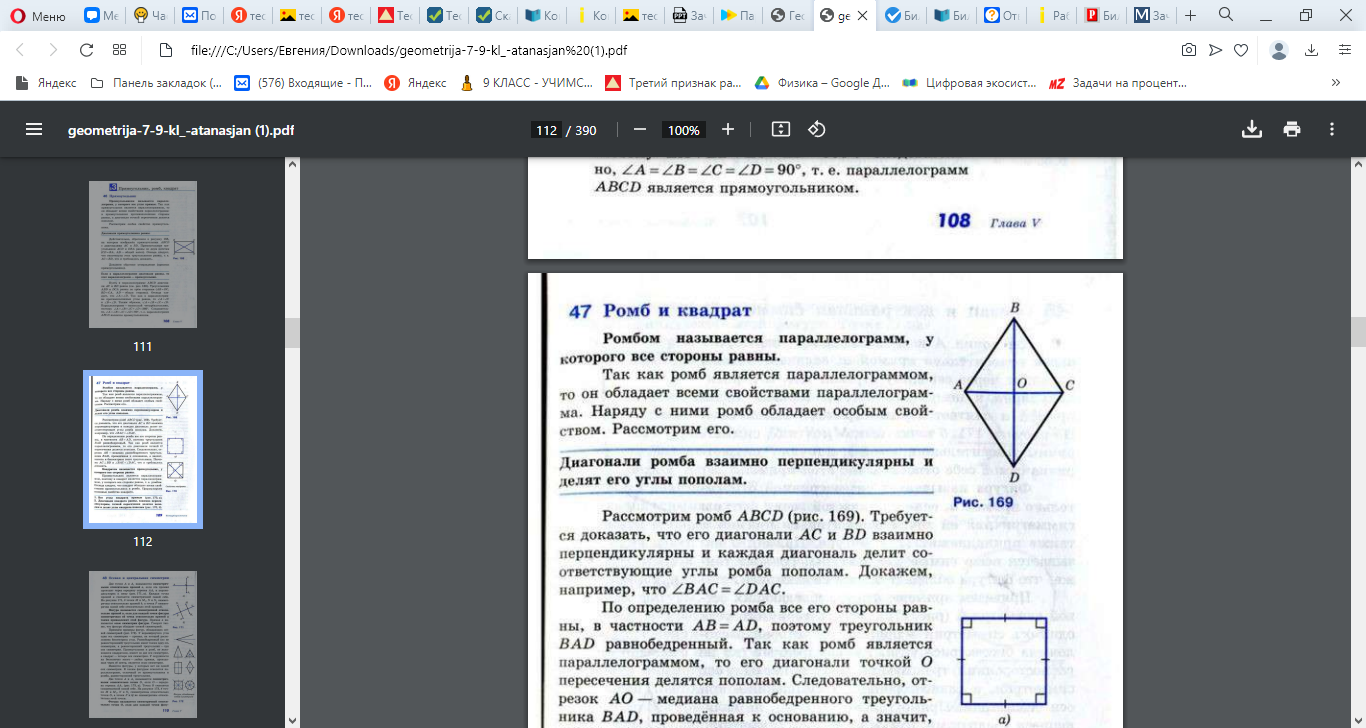 |
2. Докажите теорему о вписанном угле (любой частный случай).
Теорема
Вписанный угол измеряется половиной дуги, на которую он опирается.
1 случай
| Сторона вписанного угла проходит через центр окружности. 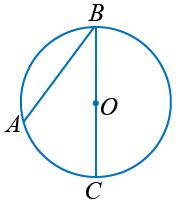 | Дано: окружность (О, R), ∠АВС - вписанный, 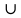 АС - внутри АС - внутри Доказать: 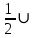 АС. АС. | ||
| Доказательство:
=> ∠B измеряется половиной дуги AC: ∠ABC = ∠ OBA = 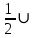 АС АСЧто и требовалось доказать | |||
2 и 3 случай на сайте: https://izamorfix.ru/matematika/planimetriya/vpisan_ugol.html
(ДОСТАТОЧНО ВЫУЧИТЬ ТОЛЬКО ПЕРВЫЙ!)
Билет 5.
-
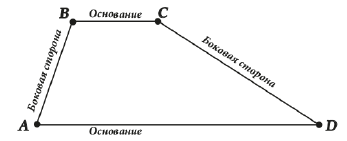
Дайте определение трапеции. Назовите виды трапеций.
Трапеция – четырехугольник, у которого две стороны параллельны, а две другие – нет.
Параллельные стороны трапеции называются основаниями.
Другие две – боковые стороны.
2. Докажите свойство отрезков касательных, проведенных к окружности из одной точки.
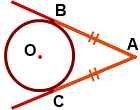
Теорема(Свойство касательных, проведенных из одной точки)
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
 AB=AC
AB=AC 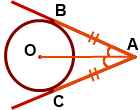 ∠BAO=∠CAO
∠BAO=∠CAO 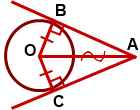 | Дано: окружность (O;R), AB и AC – касательные к окружности (O;R), B, C – точки касания. Доказать: AB=AC, ∠BAO=∠CAO. |
| Доказательство: 1. 2. Рассмотрим ∆ABO и ∆ACO: 1) катеты OB=OC=r (как радиусы) 2) гипотенуза OA — общая сторона. => ∆ ABO=∆ ACO (по катету и гипотенузе). 3. Из равенства ∆ следует равенство соответствующих сторон: AB=AC и соответствующих углов ∠BAO=∠CAO. Что и требовалось доказать | |
Билет 6.
-
Дайте определение подобных треугольников. Назовите признаки подобия треугольников.
Два треугольника называют подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Сходственные стороны треугольника – это стороны, лежащие напротив соответственно равных углов.
Первый признак подобия треугольников: Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
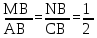

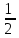 ∠AOC
∠AOC