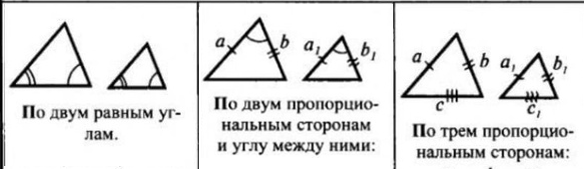
Третий признак подобия треугольников: Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.


2. Докажите признак параллелограмма (по точке пересечения диагоналей).

Теорема: Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

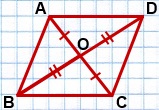Дано: ABCD – четырехугольник, АС и BD – диагонали, AC∩BD=O, AO=OC, BO=OD. Доказать: ABCD – параллелограмм

Доказательство: 1. Рассмотрим треугольники ∆AOD и ∆COB. 1) AO = OC (по условию); 2) BO = OD (по условию); 3)∠AOD = ∠COB (как вертикальные). => ∆AOD = ∆COB равны (по двум сторонам и углу между ними). 2. Из равенства треугольников => ∠ADO=∠CBO 3. ∠ADO и ∠CBO – НЛУ при прямых AD и BC и секущей BD => AD ∥ BC (по признаку параллельных прямых). 4. Аналогично, ∆AOB=∆ COD, ∠ABO=∠CDO и AB ∥ CD. 5. так как AD ∥ BC и AB ∥ CD => ABCD — параллелограмм (по определению). Что и требовалось доказать

Билет 7.

1. 
   Дайте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
   

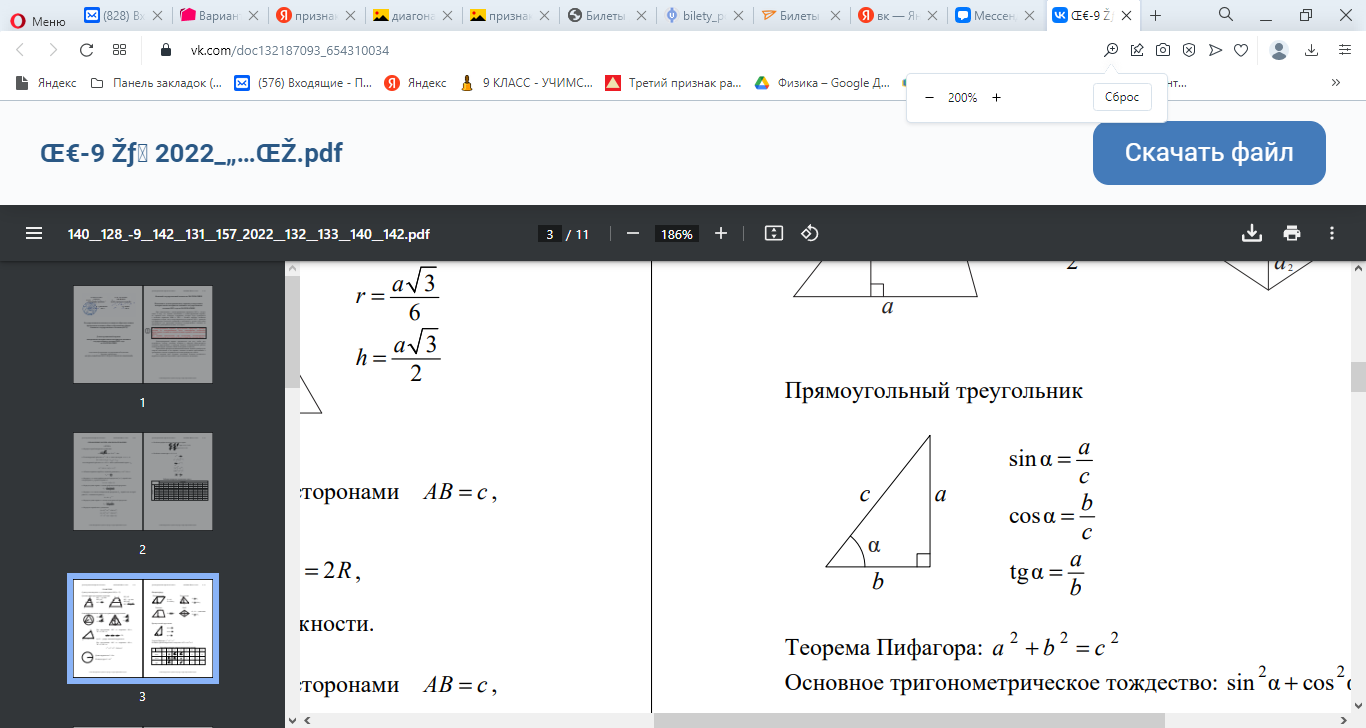
Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету

2. 
   Докажите свойство диагоналей параллелограмма
   

Теорема

---

Диагонали параллелограмма точкой пересечения делятся пополам.

	Дано: ABCD – параллелограмм, АС и BD – диагонали AC∩BD=O, Доказать: АО=ОС, ОВ=OD
Доказательство: Рассмотрим ∆AOD и ∆COB 1) ∠1=∠2 (НЛУ при AD || BC и секущей АС) 2) ∠3=∠4 (НЛУ приAD || BC и секущей BD) 3) AD=BC (как противолежащие стороны параллелограмма) => ∆AOD= ∆COB (по второму признаку). => AO=CO, BO=DO (из равенства треугольников). Что и требовалось доказать

Билет 8.

1. 
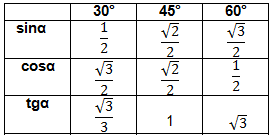
   Назовите значение синуса, косинуса и тангенса углов 30°,45°,60°.
   

2. 
   Докажите свойства противоположных сторон и углов параллелограмма.
   

Теорема (Свойства сторон и углов параллелограмма)

В параллелограмме противолежащие стороны равны и противолежащие углы равны.

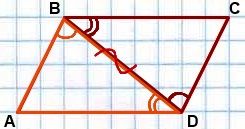Дано: ABCD – параллелограмм Доказать: AB = CD, AD = BC, ∠A=∠C, ∠B=∠D.

Доказательство: Проведем в параллелограмме ABCD диагональ BD. Рассмотрим ∆ABD и ∆CDB. 1) сторона BD — общая 2) ∠ABD=∠CDB (НЛУ при AB∥CD и секущей BD) 3) ∠ADB=∠CBD (НЛУ при AD∥BC и секущей BD) =>  ∆ABD= ∆CDB (по второму признаку). Из равенства треугольников => AB=CD, AD=BC и ∠A=∠C. Согласно п.2 и п.3 ∠ABD = ∠CDB и ∠ADB=∠ CBD =>  ∠ABC = ∠ABD+∠CBD =∠CDB+∠ADB =∠ADC => ∠B=∠D. Что и требовалось доказать

Билет 9.

1. 
   Дайте определение секущей и касательной к окружности.
   

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Секущая к окружности – это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. 

---

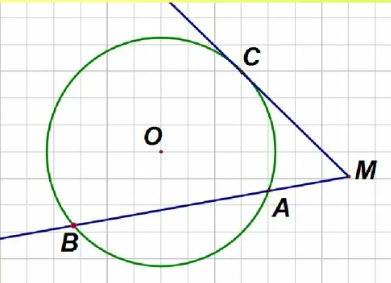
MC – касательная, AB – секущая

2. 
   Докажите свойство диагоналей прямоугольника.
   

Теорема

Диагонали прямоугольника равны.

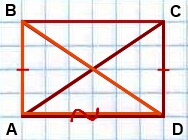	Дано: ABCD — прямоугольник, AC и BD — диагонали. Доказать: AC=BD.
Доказательство: Рассмотрим прямоугольные ∆ABD и ∆DCA. ∠BAD =∠CDA=90º (по определению прямоугольника). 1) Катеты AB = DC (как противолежащие стороны прямоугольника). 2) Катет AD — общий. => ∆ABD = ∆DCA равны (по двум катетам). Из равенства треугольников => AC = BD. Что и требовалось доказать

Билет 10.

1. 
   Дайте определение вписанного и центрального углов окружности.
   

Центральным углом называют угол, вершина которого совпадает с центром окружности. Свойство: Центральный угол равен градусной мере дуги, на которую он опирается.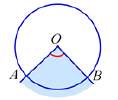
Вписанным углом называют угол, вершина которого лежит на окружности, а стороны пересекают окружность. Свойство: Вписанный угол измеряется половиной дуги, на которую он опирается.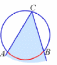

2. 
   Докажите признак параллелограмма по двум противоположным сторонам, которые равны и параллельны.
   

Теорема

Если две стороны четырехугольника параллельны и равны, то этот четырехугольник — параллелограмм.

Дано: ABCD — четырехугольник, AD=BC, AD ∥ BC. Доказать: ABCD — параллелограмм

Доказательство: 1. Проведем диагональ AC. 2. Рассмотрим ∆ABC и CDA 1) AD = BC (по условию) 2) сторона AC — общая 3)∠CAD =∠ACB (НЛУ при AD ∥ BC и секущей AC) => ∆ABC = ∆CDA (по первому признаку). 3. Из равенства треугольников => ∠ACD=∠CAB. Так как эти углы НЛУ при прямых AB и CD и секущей AC, => AB ∥ CD  (по признаку параллельности прямых). 4. В четырехугольнике ABCD: 1) AD ∥ BC (по условию) 2) AB ∥ CD (по доказанному). => ABCD — параллелограмм (по определению). Что и требовалось доказать

---

Билет №11

1. 
   Дайте определение серединного перпендикуляра к отрезку. Назовите свойство серединного перпендикуляра.
   
2. 
   Запишите вывод формулы площади треугольника, следствия, формулу Герона (без доказательства).
   

Билет №12

1. 
   Дайте определение: окружности, вписанной в многоугольник; многоугольника, описанного около окружности. Назовите свойство описанного четырехугольника.
   
2. 
   Докажите свойства диагоналей ромба.
   

Билет №13

1. 
   Дайте определение окружности, описанной около многоугольника; многоугольника, вписанного в окружность. Назовите свойства четырехугольника, вписанного в окружность.
   
2. 
   Докажите свойство биссектрисы угла
   

Билет №14

1. 
   Дайте определение: окружности, вписанной в треугольник; окружности, описанной около треугольника, нахождение центров этих окружностей.
   
2. 
   Докажите свойство углов при основании равнобедренной трапеции.
   

Билет №15

1. 
   Сформулируйте теорему Фалеса.
   
2. 
   Докажите свойство отрезков пересекающихся хорд.
   

---

Смотрите также файлы

• Э. Мэйо родился в Аделаиде, столице Южной Австралии. Первоначально получал образование в области медицины в Австралии и Шотландии, но, не закончив обучение, стал заниматься поиском альтернативной специальности.docx

• Особенности государственной политики в области борьбы с бедностью.pdf

• Текст для самоконтроля.docx

• Надувной радиолокационный отражатель.docx

• С колей Гумилевым своим будущим мужем первым мужем Аня позн комилась в 1904 году в сочельник. Ходили покупать игрушки для елки. Был чудес()ный солнечный день.docx