Файл: Задача 1 4 Решение 5 Задача 2 7 Решение 9 Задача 3 10 Решение 11 Задача 4 11 Решение 12 Задача 5 13.docx

Решение

Анализируем 9 вариант задачи.

Для сопоставления рабочей загруженности нескольких предприятий связи создаем модель и выполняем вычисления.

Результаты вычислений представлены в таблице:

График	а	b	c	d	e
Первое предприятие	-0,59012	-0,60172	-0,43948	-0,59688	-0,58763
Второе предприятие	-0,58083	-0,4927	-0,62286	-0,5937	-0,58982
Третье предприятие	-0,58323	-0,56721	-0,56276	-0,49796	-0,18004

Построим графические зависимости, поясняющие полученные результаты (рис. 2):



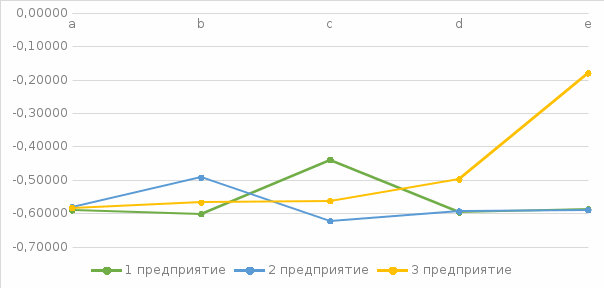
Рисунок 2

Задача 6

Известно, что максимальный размер коробки для почтовой посылки (тары) определяется величиной трех параметров: длиной (L), шириной (W) и высотой (H). Известны ограничения: длина коробки (L) плюс периметр поперечного сечения не превосходят Е (см).

Это означает, что E = L  2H  2W

Полагаем, что L = 2H = 2W , L = E / 3

Требуется:

1. 
   Найти максимальный размер тары, если известны параметры, представленные в таблице 6- 1.
   
2. 
   вычислить максимальное количество упаковочных коробок в 1 м3
   

Таблица 6-1

Номер варианта	Размер L (см.)	Параметр Е (см 3)
9	56	26500

Пояснить полученный результат

Решение

По условию имеем L = 2H = 2W. Следовательно можем найти значения H и W: для этого L = 44 делим на 2. Получаем H = W = 28.

---

По формуле =(B3+2*D3+2*E3) находим максимальный размер коробки для почтовой посылки (тары) = 168, которое выполняет условие и не превосходит E = 26500.

Можем найти значение Q: для этого E = 26500 делим на максимальный размер коробки для почтовой посылки (тары) = 168. Получаем Q = 158.

Результаты вычислений представлены в таблице:

Номер варианта	Размер L (см.)	Параметр Е (см 3)	Вычислить H (см.)	Вычислить W (см.)	Вычислить Q (штуки) в 1 м3
3	56	26500	28	28	158

В ходе выполнения задачи №6 мы нашли максимальный размер тары = 168 и вычислили максимальное количество упаковочных коробок в 1 м3 = 158.

---

Задача 7

Имеется процесс, характеризующий работу телекоммуникационного узла связи. По результатам наблюдений создана аналитическая модель, отражающая некоторые особенности рабочих процессов.

Модель представлена серией выходных Y параметров

Время суток	1 Состояние системы	2 Состояние системы	3 Состояние системы	4 Состояние системы	5 Состояние системы
0	224,28	259,56	287,28	297,36	322,56
1	153,08	177,16	196,08	202,96	220,16
2	202,92	234,84	259,92	269,04	291,84
3	234,96	271,92	300,96	311,52	337,92
4	89	103	114	118	128
5	185,12	214,24	237,12	245,44	266,24
6	81,88	94,76	104,88	108,56	117,76
7	234,96	271,92	300,96	311,52	337,92
8	217,16	251,32	278,16	287,92	312,32
9	149,52	173,04	191,52	198,24	215,04
10	284,8	329,6	364,8	377,6	409,6
11	299,04	346,08	383,04	396,48	430,08
12	170,88	197,76	218,88	226,56	245,76
13	341,76	395,52	437,76	453,12	491,52
14	352,44	407,88	451,44	467,28	506,88
15	10,68	12,36	13,68	14,16	15,36
16	252,76	292,52	323,76	335,12	363,52
17	288,36	333,72	369,36	382,32	414,72
18	153,08	177,16	196,08	202,96	220,16
19	256,32	296,64	328,32	339,84	368,64
20	231,4	267,8	296,4	306,8	332,8
21	167,32	193,64	214,32	221,84	240,64
22	277,68	321,36	355,68	368,16	399,36
23	85,44	98,88	109,44	113,28	122,88
24	42,72	49,44	54,72	56,64	61,44

---

Найти:

1. 
   Корреляцию первого процесса с остальными процессами
   
2. 
   Вычислить дисперсию каждого процесса
   
3. 
   Вычислить оценку подобия процессов
   

---

Решение

Вычислим корреляцию первого процесса с остальными процессами.

Результаты вычислений представлены в таблице:

Корреляция
1	2	3	4
1,000000	1,000000	1,000000	1,000000

Вычислим дисперсию каждого процесса.

Результаты вычислений представлены в таблице:

Дисперсия
1	2	3	4
8 063,03	10 799,23	13 229,03	14 173,67

Вычислим оценку подобия процессов.

Результаты вычислений представлены в таблице:

Оценка подобия
1	2	3	4
9 802,62	13 129,15	16 083,18	17 231,63

Задача 8

Имеется набор систем, таких что кластер характеризуется функцией выхода:



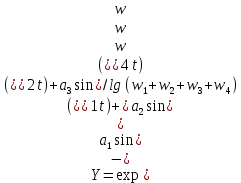
Найти:

1. 
   создать математическую модель кластера
   
2. 
   воспроизвести графический образ кластера, используя данные
   

№	w	а
1	152,3	14,8
2	1800,2	47,85
3	42,1	28,3
4	15,8	14,8
5	15234	47,85
6	425	28,3

---