Итак, данный метод предполагает следующие шаги:

1. 
   построение множества достижимых целей (альтернатив) в пространстве критериев (выбранных для оптимизации);
   
2. 
   создание графиков, визуально отображающих кривые объективного замещения между различными парами критериев;
   
3. 
   выбор оптимальной (компромиссной) цели;
   
4. 
   расчет выбранной цели и выработка стратегии по внедрению выбранной системы [1].
   

Рассмотрим данный метод более подробно на примере. Пусть существуют четыре альтернативных друг другу проекта; обозначим их через x1, x2, x3, x4, причем x_i > 0 (i = 1...4), Σ_xi = 1.

Пусть существует три критерия, которые мы выбрали для оценки, остальные были приняты как константы (или были наложены ограничения).
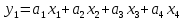— критерий общей стоимости системы,
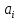— стоимость i-альтернативы.

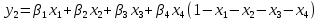— критерий риска, оставшегося после внедрения системы,
Где 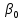— риск до внедрения системы;

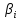— остаточный риск i-й альтернативы;
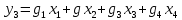— критерий надежности.
Рассмотрим альтернативы, оценив их по критериям 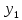и 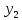. Пусть заданы такие значения коэффициентов, что в результате получается следующий график (рис. 3).

Поскольку оба параметра необходимо уменьшить (стоимость и риски), то юго-западная граница области содержит подмножество парето-оптимальных решений. К этой области принадлежит одна единственная точка с координатами (2, 1). Она является парето-оптимальной, потому что при одном и том же уровне риска ее стоимость меньше чем у точки (4, 1), иначе говоря, увеличение стоимости после точки (2, 1) не приводит к значительному снижению рисков, значит решение (4, 1) неоптимально [1].



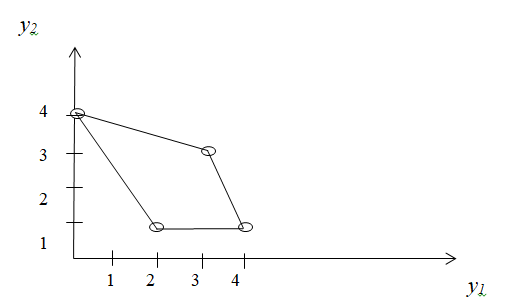
Рис. 3 – Кривая объективного замещения стоимости и остаточных рисков

Метод достижимых целей позволяет создавать огромное множество парных критериальных графиков, однако для каждого такого графика будет иметься своя область эджварто-парето (ОЭП или недоминируемое множество), при чем эти множества для каждой пары критериев не обязательно должны пересекаться. Потому если необходимо найти решения оптимальные сразу по не сколь ким показателям (трем и более), то надо располагать альтернативы в трехмерном (n-мерном) пространстве отобранных критериев.

---

Однако анализировать трехмерные пространства с целью поиска областей оптимальных решений трудно, поэтому предлагается использовать серию рисунков из двумерных сечений трехмерной фигуры, содержащих множество допустимых решений. Анализ двумерных сечений аналогичен анализу альтернатив в плоскости. При числе критериев более трех на оставшиеся необходимо накладывать ограничения, использовать методы свертки и сечений многомерных пространств. Так, например, при одновременной оптимизации четырех критериев получается четырехмерное пространство (пространственно-временной континуум — длина, ширина, высота и время). Оно может быть представлено в виде одномерного массива времени, элементы которого содержат трехмерное пространство на конкретный момент времени, которое, в свою очередь, сворачивается при помощи наборов двумерных сечений.

Визуально это можно отобразить при помощи анимации, видео или переключателя кадров, где каждый кадр — набор сечений в данный момент времени (под словами длина, ширина, высота, время понимаем критерии, выбранные для оптимизации); таким образом, беря значение четвертого критерия за константу, можно отобразить двумерное сечение для этой константы. В случае пяти критериев можно представить их как двумерный массив сечений, или как одномерный массив пятого критерия, элементами которого является одномерный массив четвертого критерия (время), который содержит наборы двумерных сечений (двумерное представление трехмерного объекта).

В этом случае надо закреплять уже два параметра (четвертый и пятый критерии) и вычислять для этих констант двумерные сечения.

Задача выбора альтернативных проектов построения систем в пространстве трудно формализуемая, многокритериальная и происходит в условиях частичной неопределенности (не все альтернативы и критерии заданы и описаны изначально), а значит, не поддается четкой алгоритмизации. Поэтому система поддержки принятия решений должна только делать расчеты для выбранных решений, формировать множества оптимальных решений и отображать их графически, а не принимать решение о выборе конкретной оптимальной альтернативы из построенного множества.

Само принятие решения должно остаться за человеком — специалистом в области защиты информации, который, руководствуясь собственным опытом, знаниями и интуицией, сможет выбрать верное решение. Поэтому главная задача системы поддержки принятия парето-оптимальных решений в области проектирования— помочь лицам, принимающим решения принять оптимальное (компромиссное) решение в заданных условиях, причем достаточно оперативно и наглядно, а также обосновано.

---

Заключение

Множеством Парето называется множество, безусловно, несравнимых альтернатив, оставшихся после отбрасывания всех, безусловно, худших альтернатив.

Оптимальность по Парето — такое состояние системы, при котором значение каждого частного показателя (критерия), характеризующего систему (принятия решений), не может быть улучшено без ухудшения других.

Таким образом, по словам самого Парето: «Всякое изменение, которое никому не приносит убытков, а некоторым приносит пользу (по их собственной оценке), является улучшением». Значит, признается право на все изменения, которые не приносят никому дополнительного вреда и оптимальным решением принимается такое, которое является доминирующим.

Рассмотрев наиболее распространенные подходы к поиску оптимального решения многокритериальных задач, в том числе в условиях неопределенности, на практике именно метод парето-оптимальности будет наиболее удобным и эффективным, поскольку позволяет выделить ряд критериев, не вносящих существенный вклад в достижение оптимальной эффективности и выбрать оптимального решение[1].

Задача выбора альтернативных проектов построения систем в пространстве трудно формализуемая, многокритериальная и происходит в условиях частичной неопределенности (не все альтернативы и критерии заданы и описаны изначально), а значит, не поддается четкой алгоритмизации. Поэтому система поддержки принятия решений должна только делать расчеты для выбранных решений, формировать множества оптимальных решений и отображать их графически, а не принимать решение о выборе конкретной оптимальной альтернативы из построенного множества.

Само принятие решения должно остаться за человеком — специалистом в области защиты информации, который, руководствуясь собственным опытом, знаниями и интуицией, сможет выбрать верное решение. Поэтому главная задача системы поддержки принятия парето-оптимальных решений в области проектирования— помочь лицам, принимающим решения принять оптимальное (компромиссное) решение в заданных условиях, причем достаточно оперативно и наглядно, а также обосновано.
Список используемых источников

1. 
   Баранова Е. К. Моделирование системы защиты информации: Практикум: Учебное пособие / Е.К.Баранова, А.В.Бабаш// М.: ИЦ РИОР: НИЦ ИНФРА-М, 2015 - 120 с.
   
2. 
   Ногин В.Д. Расслоение конечного множества Парето/ Ногин В.Д.// Актуальные проблемы гуманитарных и естественных наук. 2015. № 12-1. С. 28-30.
   
3. 
   Часовников С.Н. Портфель финансовых инструментов: оптимальность по Эджворту – Парето/ Часовников С.Н., Кирьянов И.В.// Сибирская финансовая школа. 2012. № 3 (92). С. 84-90.
   

---

---

Смотрите также файлы

• Практическое задание 4 Тем Окружение бизнеспроекта Тема Влияние в бизнеспроекте.docx

• Докладсообщение Система дополнительного образования.docx

• Имя физического лица как предмет сделки от критики до признания в гражданском праве т. С. Яценко я.docx

• И. С. Бастенрешения конституционного судароссийской федерации как источник права.pdf

• .docx