Файл: Скалярное произведение векторов. Решение задач (урок 5).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(рис. 24). Если эти векторы не являются сонаправлеными, то угол между  и
и 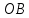 образуют угол
образуют угол 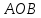 и градусную меру этого угла обозначим через
и градусную меру этого угла обозначим через  и будем говорить, что угол между векторами
и будем говорить, что угол между векторами  и
и  равен
равен  , принято, что
, принято, что 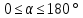 .
.
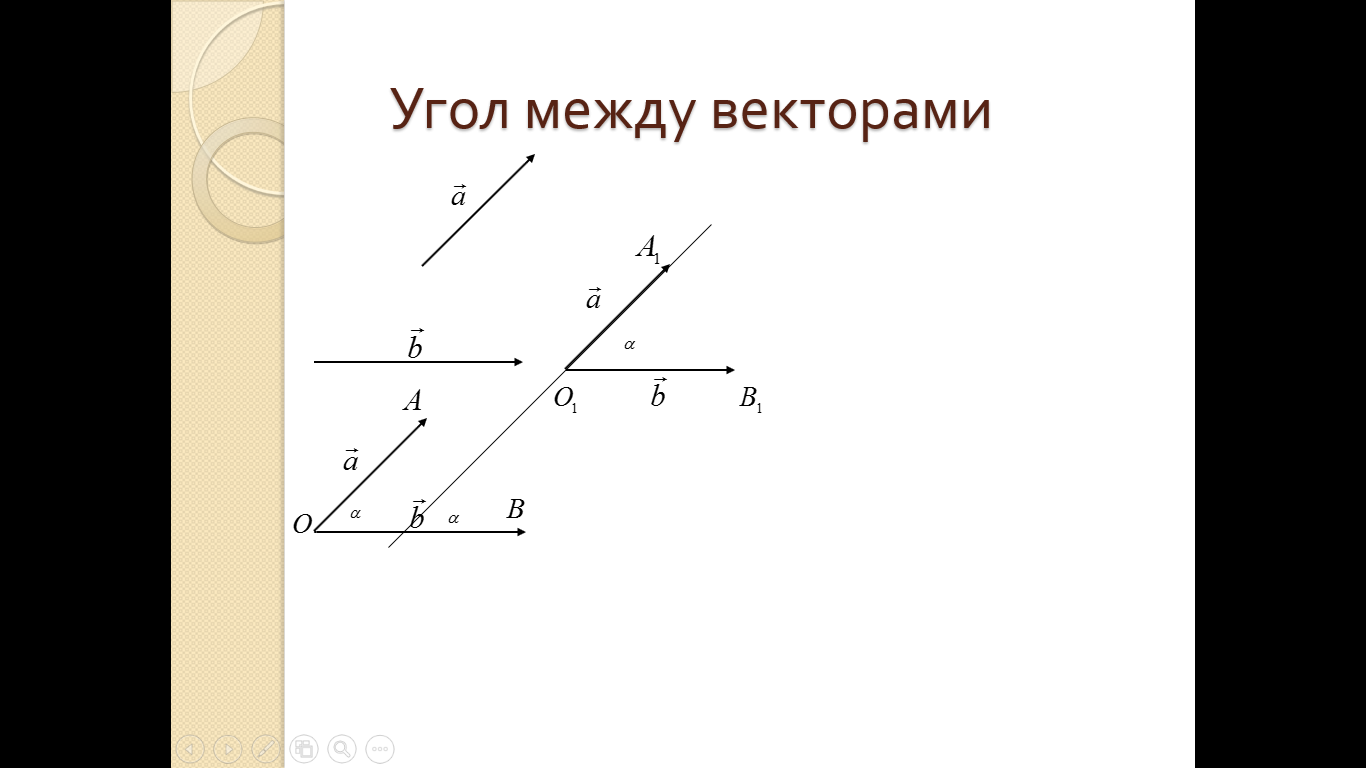
Рис. 24
Таким образом, углом между любыми двумя ненулевыми векторами и
и  называется угол между равными им векторами с общим началом. Обратите внимание, что угол
называется угол между равными им векторами с общим началом. Обратите внимание, что угол  не зависит от выбора точки
не зависит от выбора точки  от которой откладываются вектора.
от которой откладываются вектора.
Если же вектора параллельны или один из них равен нулю, то угол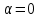 по определению.
по определению.
Угол между векторами и
и  обозначается так:
обозначается так: 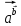 .
.
Рассмотрим примеры (рис. 25).

Рис. 25
Два вектора называются перпендикулярными, если угол между ними равен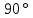 .
.
Скажите, глядя на рисунок, какие вектора будут перпендикулярными? ( и
и 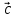 ,
, 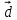 и
и 
,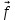 и
и  )
)
Теперь, зная, как определить угол между векторами, мы можем определить скалярное произведение векторов.
Скалярным произведением векторов называется произведение их длин на косинус угла между ними: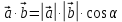
Запишите формулу в тетрадь и обведите в рамку.
Таким образом, чтобы найти скалярное произведение нужно знать длины векторов и угол между ними.
Решим пример.
Дано: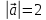 ,
, 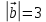 ,
,
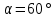 .
.
Найти: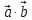
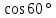 =
=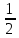 ;
; 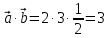 .
.
Обратите внимание, что в результате скалярного произведение обязательно будет число.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Если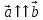 (сонаправлены), то получаем
(сонаправлены), то получаем 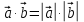 . В частности,
. В частности, 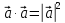 . Скалярное произведение
. Скалярное произведение 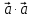 называется скалярным квадратом вектора
называется скалярным квадратом вектора  и обозначается
и обозначается 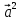 . Таким образом, скалярный квадрат вектора равен квадрату его длины.
. Таким образом, скалярный квадрат вектора равен квадрату его длины.
Скалярное произведение двух векторов можно вычислить, зная координаты векторов. Запишем теорему.
Теорема. В прямоугольной системе координат скалярное произведение векторов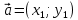 и
и 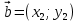 выражается формулой
выражается формулой 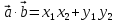 .
.
Доказательство рассмотрите дома самостоятельно.
Давайте теперь посмотрим какими свойствами обладает скалярное произведение.
Из теоремы следует два утверждения.
Следствие 1: Ненулевые векторы и
и  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда 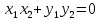 .
.
Следствие 2: Косинус угла между ненулевыми векторами векторов
между ненулевыми векторами векторов  и
и  выражается формулой
выражается формулой 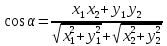 .
.
Давайте теперь посмотрим какими свойствами обладает скалярное произведение.
Запишите подзаголовок: свойства скалярного произведения.
Для любых векторов ,
,  ,
,  и любого числа
и любого числа 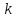 справедливы соотношения:
справедливы соотношения:
1о.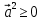 , причем
, причем 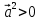 при
при 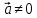 .
.
2о.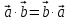 (переместительный закон).
(переместительный закон).
3о.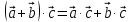 (распределительный закон).
(распределительный закон).
4о.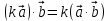 (сочетательный закон).
(сочетательный закон).
Давайте докажем с вами эти свойства.
Свойство 1о непосредственно следует из формулы , а свойство 2о – из определения скалярного произведения.
, а свойство 2о – из определения скалярного произведения.
Докажем свойства 3о и 4о.
Введём прямоугольную систему координат и обозначим координаты векторов ,
,  ,
,  так:
так:  ,
,  ,
, 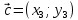
.
Используя формулу скалярного произведения в координатах, получаем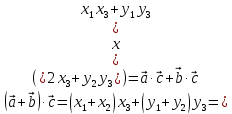 .
.
Свойство 3о доказано.
Докажем теперь свойство 4о. Вектор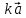 имеет координаты
имеет координаты 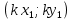 , поэтому
, поэтому 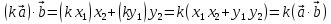 .
.
6. Физкультминутка
Учащиеся выполняют за учителем.
Упражнение 1. Сжать пальцы в кулак и сделать круговые движения кистью влево, затем вправо.
Упражнение 2. С силой сжимать и разжимать пальцы, пока они не устанут.
Упражнение 3. Выпрямить пальцы, большой палец отвести в сторону и проделать им круговые движения сначала влево, затем вправо.
Также и упражнения для глаз.

Рис. 26
7. Закрепление
Теперь давайте выполним с вами задания.
№ 1039. Диагонали квадрата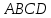 пересекаются в точке
пересекаются в точке  . Найдите угол между векторами: а)
. Найдите угол между векторами: а)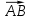 и
и 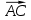 ; б)
; б)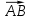 и
и 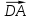 ; в)
; в)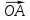 и
и 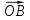 ; г)
; г)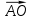 и
и 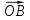 .
.
Выполняют у доски (а) и (б) с пояснением, (в) и (г) выполняют самостоятельно в тетради.
№ 1041 (а, б). Вычислите скалярное произведение векторов и
и  , если
, если  ,
,  , а угол между ними равен: а)
, а угол между ними равен: а)  ; б)
; б)  .
.
Какую формулу будем использовать? А) выполняют у доски, а б) самостоятельно в тетради.
№ 1044 (а, б). Вычислите скалярное произведение векторов и
и  , если: а)
, если: а) 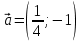 и
и 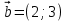 ; б)
; б) 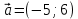 и
и 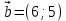 .
.
Как будем находить? (а) выполняют у доски, а (б) самостоятельно в тетради.
№ 1048. Найдите косинусы углов треугольника с вершинами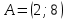 ,
, 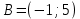 и
и 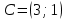 .
.
По какой формуле будем вычислять? Выполняют у доски.
8. Подведение итогов
Учитель предлагает вспомнить цель и задачи урока.
Ответить на вопрос: «Достигнута ли цель урока?»
Сегодня на занятии мы вспомнили понятие вектора, виды векторов, а также познакомились со скалярным произведением, с их свойствами, научились решать простейшие задачи на данную тему.
Я думаю, что у вас сложилось более полное представление о векторах. И у меня появилась уверенность, что с решением простейших задач на данную тему вы справитесь.
Фронтальным опросом вместе с учащимися подводятся итоги занятия:
Какие операции теперь мы можем выполнять над векторами? (Сложение, вычитание, умножение на число и скалярное произведение векторов)
Скажите, что нужно знать для нахождения скалярного произведения? (Длины векторов и угол между ними)
Чем отличаемся изученное действие от предыдущих? (В результате получается всегда число)
А если векторы заданы в координатах, мы можем найти скалярное произведение? (Да, по формуле, данной в теореме)
9. Рефлексия
Учитель раздаёт всем учащимся карточки-анкеты под названием «Насытились?», которые в совокупности объединяются в книгу жалоб и пожеланий ресторана «Скалярное произведение векторов», посетителями которого только что были учащиеся. Ученикам предлагается поделиться своими ощущениями.
«Насытились?»
Я съел бы еще этого …
________________________________________________________________________________________________________________________________________
Больше всего мне понравилось …
________________________________________________________________________________________________________________________________________
Я почти переварил …
 и
и 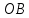 образуют угол
образуют угол 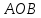 и градусную меру этого угла обозначим через
и градусную меру этого угла обозначим через  и будем говорить, что угол между векторами
и будем говорить, что угол между векторами  и
и  равен
равен  , принято, что
, принято, что 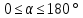 .
.
Рис. 24
Таким образом, углом между любыми двумя ненулевыми векторами
 и
и  называется угол между равными им векторами с общим началом. Обратите внимание, что угол
называется угол между равными им векторами с общим началом. Обратите внимание, что угол  не зависит от выбора точки
не зависит от выбора точки  от которой откладываются вектора.
от которой откладываются вектора.Если же вектора параллельны или один из них равен нулю, то угол
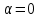 по определению.
по определению. Угол между векторами
 и
и  обозначается так:
обозначается так: 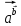 .
.Рассмотрим примеры (рис. 25).

Рис. 25
Два вектора называются перпендикулярными, если угол между ними равен
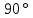 .
.Скажите, глядя на рисунок, какие вектора будут перпендикулярными? (
 и
и 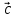 ,
, 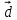 и
и 
,
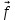 и
и  )
)Теперь, зная, как определить угол между векторами, мы можем определить скалярное произведение векторов.
Скалярным произведением векторов называется произведение их длин на косинус угла между ними:
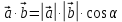
Запишите формулу в тетрадь и обведите в рамку.
Таким образом, чтобы найти скалярное произведение нужно знать длины векторов и угол между ними.
Решим пример.
Дано:
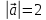 ,
, 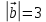 ,
,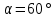 .
.Найти:
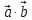
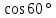 =
=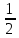 ;
; 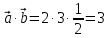 .
.Обратите внимание, что в результате скалярного произведение обязательно будет число.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Если
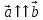 (сонаправлены), то получаем
(сонаправлены), то получаем 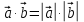 . В частности,
. В частности, 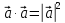 . Скалярное произведение
. Скалярное произведение 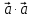 называется скалярным квадратом вектора
называется скалярным квадратом вектора  и обозначается
и обозначается 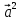 . Таким образом, скалярный квадрат вектора равен квадрату его длины.
. Таким образом, скалярный квадрат вектора равен квадрату его длины.Скалярное произведение двух векторов можно вычислить, зная координаты векторов. Запишем теорему.
Теорема. В прямоугольной системе координат скалярное произведение векторов
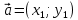 и
и 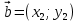 выражается формулой
выражается формулой 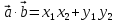 .
.Доказательство рассмотрите дома самостоятельно.
Давайте теперь посмотрим какими свойствами обладает скалярное произведение.
Из теоремы следует два утверждения.
Следствие 1: Ненулевые векторы
 и
и  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда 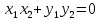 .
.Следствие 2: Косинус угла
 между ненулевыми векторами векторов
между ненулевыми векторами векторов  и
и  выражается формулой
выражается формулой 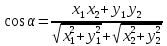 .
.Давайте теперь посмотрим какими свойствами обладает скалярное произведение.
Запишите подзаголовок: свойства скалярного произведения.
Для любых векторов
 ,
,  ,
,  и любого числа
и любого числа 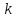 справедливы соотношения:
справедливы соотношения: 1о.
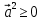 , причем
, причем 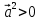 при
при 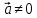 .
. 2о.
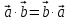 (переместительный закон).
(переместительный закон). 3о.
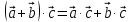 (распределительный закон).
(распределительный закон). 4о.
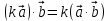 (сочетательный закон).
(сочетательный закон).Давайте докажем с вами эти свойства.
Свойство 1о непосредственно следует из формулы
 , а свойство 2о – из определения скалярного произведения.
, а свойство 2о – из определения скалярного произведения.Докажем свойства 3о и 4о.
Введём прямоугольную систему координат и обозначим координаты векторов
 ,
,  ,
,  так:
так:  ,
,  ,
, 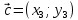
.
Используя формулу скалярного произведения в координатах, получаем
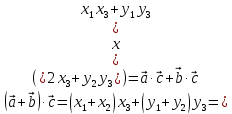 .
.Свойство 3о доказано.
Докажем теперь свойство 4о. Вектор
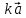 имеет координаты
имеет координаты 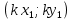 , поэтому
, поэтому 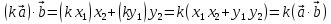 .
.6. Физкультминутка
Учащиеся выполняют за учителем.
Упражнение 1. Сжать пальцы в кулак и сделать круговые движения кистью влево, затем вправо.
Упражнение 2. С силой сжимать и разжимать пальцы, пока они не устанут.
Упражнение 3. Выпрямить пальцы, большой палец отвести в сторону и проделать им круговые движения сначала влево, затем вправо.
Также и упражнения для глаз.

Рис. 26
7. Закрепление
Теперь давайте выполним с вами задания.
№ 1039. Диагонали квадрата
 пересекаются в точке
пересекаются в точке  . Найдите угол между векторами: а)
. Найдите угол между векторами: а)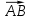 и
и 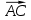 ; б)
; б)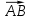 и
и 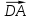 ; в)
; в)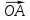 и
и 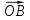 ; г)
; г)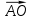 и
и 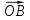 .
.Выполняют у доски (а) и (б) с пояснением, (в) и (г) выполняют самостоятельно в тетради.
№ 1041 (а, б). Вычислите скалярное произведение векторов
 и
и  , если
, если  ,
,  , а угол между ними равен: а)
, а угол между ними равен: а)  ; б)
; б)  .
.Какую формулу будем использовать? А) выполняют у доски, а б) самостоятельно в тетради.
№ 1044 (а, б). Вычислите скалярное произведение векторов
 и
и  , если: а)
, если: а) 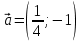 и
и 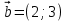 ; б)
; б) 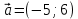 и
и 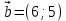 .
. Как будем находить? (а) выполняют у доски, а (б) самостоятельно в тетради.
№ 1048. Найдите косинусы углов треугольника с вершинами
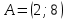 ,
, 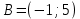 и
и 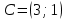 .
.По какой формуле будем вычислять? Выполняют у доски.
8. Подведение итогов
Учитель предлагает вспомнить цель и задачи урока.
Ответить на вопрос: «Достигнута ли цель урока?»
Сегодня на занятии мы вспомнили понятие вектора, виды векторов, а также познакомились со скалярным произведением, с их свойствами, научились решать простейшие задачи на данную тему.
Я думаю, что у вас сложилось более полное представление о векторах. И у меня появилась уверенность, что с решением простейших задач на данную тему вы справитесь.
Фронтальным опросом вместе с учащимися подводятся итоги занятия:
Какие операции теперь мы можем выполнять над векторами? (Сложение, вычитание, умножение на число и скалярное произведение векторов)
Скажите, что нужно знать для нахождения скалярного произведения? (Длины векторов и угол между ними)
Чем отличаемся изученное действие от предыдущих? (В результате получается всегда число)
А если векторы заданы в координатах, мы можем найти скалярное произведение? (Да, по формуле, данной в теореме)
9. Рефлексия
Учитель раздаёт всем учащимся карточки-анкеты под названием «Насытились?», которые в совокупности объединяются в книгу жалоб и пожеланий ресторана «Скалярное произведение векторов», посетителями которого только что были учащиеся. Ученикам предлагается поделиться своими ощущениями.
«Насытились?»
Я съел бы еще этого …
________________________________________________________________________________________________________________________________________
Больше всего мне понравилось …
________________________________________________________________________________________________________________________________________
Я почти переварил …