Н а этом графике показаны безразмерные относительные фазовые проницаемости k ₁ и k ₂; s_А – связанная компонента первой, более смачивающей фазы (для воды обычно около 20%).

Характерная несимметричная форма кривых относительной проницаемости объясняется тем, что при одной и той же насыщенности более смачивающая фаза занимает преимущественно мелкие поры и относительная проницаемость у неё меньше. При малых насыщенностях часть каждой из фаз находится в несвязном состоянии в виде изолированных мелких капель или целиков и не участвует в движении. Поэтому, начиная с некоторой насыщенности, каждая фаза полностью переходит в несвязное состояние и её относительная проницаемость становится равной нулю, т.е. k₁(s)=0 при sA, k₂(s)=0 при s>1-s_A. Движение этой фазы может происходить только, если s > s_А. Для второй фазы связанная компонента равна 1- s_A. Заметим, что хотя речь идет о совместной фильтрации двух несмешивающих жидкостей, приходится различать вытесняющую и вытесняемые фазы, т.к. относительные проницаемости различны в зависимости от того, какая из фаз (более или менее смачиваемая) первоначально заполняла пористую среду, т.е. существует гистерезис относительных проницаемостей.

Сумма относительных проницаемостей для каждого фиксированного значения  меньше 1:

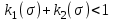, 0<<1.

Это означает, что присутствие связанной смачивающей фазы мало влияет на течение не смачивающей жидкости, тогда как присутствие остаточной не смачивающей фазы значительно "стесняет" движение смачивающей фазы.

Введенные выше понятия можно обобщить на случай совместного движения трех несмешивающихся флюидов: нефти, газа и воды. Если обозначить эти флюиды индексами "н", "г" и "в", то можно ввести относительные проницаемости, точно так же как это было сделано для двух жидкостей. При этом фазовые проницаемости являются уже функциями двух независимых насыщенностей и определяются из треугольных диаграмм (рис.5).

На треугольной диаграмме показаны границы преобладания фаз. Из диаграммы видно, что при газонасыщенности более 35 % поток состоит только из газа, зелёная область показывает на наличие всех фаз. По диаграмме можно определить, какие компоненты движутся в пласте при данном соотношении величин насыщенности пор фазами.

Характер зависимостей определяется различной степенью смачивания твердых зерен породы фазами, причем оказывается, что относительная проницаемость зависит только от водонасыщенности - наиболее проницаемой фазы - воды, и почти не зависит от нефте- и газонасыщенности.

На основании экспериментов можно считать, что относительная фазовая проницаемость в многофазном потоке почти не зависит от вязкости жидкости, ее плотности, внутрижидкостного натяжения, градиента давления.

Г) Коллекторские свойства трещиноватых пород.

Подавляющая часть нефтяных и газовых месторождений приурочена к коллекторам трёх типов – гранулярным, трещинным и смешанного строения. К первому типу относятся коллекторы, сложенные песчано-алевритовыми породами, поровое пространство которых состоит из межзерновых полостей. Подобным строением порового пространства характеризуются также некоторые пласты известняков и доломитов. В чисто трещиноватых коллекторах (сложенных преимущественно карбонатами) поровое пространство образуется системой трещин. При этом участки коллектора между трещинами представляют собой плотные малопроницаемые нетрещиноватые блоки пород, поровое пространство которых практически не участвует в процессах фильтрации. На практике, однако, чаще всего встречаются трещиноватые коллекторы смешанного типа, поровое пространство которых включает как системы трещин, так и поровое пространство блоков, а также каверны и карст.

Трещинная проницаемость сланцев, известняков, доломитов, алевролитов и песчаников, изменяющаяся от 15 до 40 фм², намного больше межгранулярной, не превышающей обычно 0,1 фм².

Для расчета коэффициента трещинной проницаемости k_пр может быть использованы формула

k_пр=8,45∙10⁶b²k_п (10)

где b – раскрытость трещин, мкм; k_n=Tb – коэффициент тре­щинной пористости (здесь Т – объемная плотность трещин, м²/м³), %.

Определяют также трещинную проницаемость в больших шлифах под микроскопом. При использовании этого способа получают: 1) раскрытость b (в мкм) микротрещин по измерениям в шлифе, 2) суммарную длину l(в см) микротрещин в шлифе, 3) площадь шлифа S_ш (в см²).

Для косвенной оценки k_np применяют величину L=l/Г, где Г – густота трещин – число трещин на единицу длины перпендикуляра, восставленного к плоскости трещин в шлифе. Параметр Грассчитывают по определенным в шлифе суммарной длине (протяженности) l трещин, секущих шлиф, и площади S_шс использованием формулы: Г=Сl/S_ш, где С – числовой коэффи­циент, принимающий в зависимости от геометрии систем трещин разные значения.

Так как раскрытость трещин у литологически различных трещинных пород примерно постоянна (14-15 мкм), то расстояние между трещинами L может служить для примерной оценки проницаемости пород. Это расстояние изменяется от 8 до 140 мкм. Соответственно изменяется и проницаемость трещиноватых пород; последняя равна, например, 0,5 фм² для доломи­тов с L=14 см и 24 фм² для мергелей с L=0,8 см.

Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.

Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

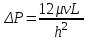, (11)

где h – высота трещины;

v – линейная скорость фильтрации.

Подставив это выражение в уравнение Дарси, получим:

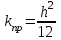. (12)

С учетом, что r измеряется в [см], а коэффициент проницаемости в [Д], вводим соответствующий коэффициент пересчета = 9,869·10 ^–9. Тогда, коэффициент проницаемости при фильтрации через трещину оценивается:

К_пр = h² /(12 · 9,869·10 ^–9) = 84,4 · 10⁵ h². (13)

  1   2   3

---

Д) Состав природных газов и их свойства. Коэффициент сверхсжимаемости смеси газов и методы его расчета, плотность природного газа.

Природные газы, добываемые из газовых, газоконденсатных и нефтяных месторождений, состоят из углеводородов (СН₄ – С₄Н_10, для Н.У. и С.У.), а также неуглеводородных компонентов (H₂S, N₂, CO, CO₂, Ar, H₂, He).

При нормальных и стандартных условиях в газообразном состоянии существуют только углеводороды С₁–С₄. Углеводороды С₅ и выше в нормальных условиях находятся в жидком состоянии.

Газы, добываемые из чисто газовых месторождений, содержат более 95% метана (табл. 1).

Таблица 1. Химический состав газа газовых месторождений, об. %

Месторождение	СН4	С2Н6	С3Н8	С4Н10	С5Н12	N2	СО2	Относит. плотность
Северо-Ставропольское	98,9	0,29	0,16	0,05	–	0,4	0,2	0,56
Уренгойское	98,84	0,1	0,03	0,02	0,01	1,7	0,3	0,56
Шатлыкское	95,58	1,99	0,35	0,1	0,05	0,78	1,15	0,58
Медвежье	98,78	0,1	0,02	–	–	1,0	0,1	0,56

Содержание метана на газоконденсатных месторождениях – 75-95% (табл. 2).

Таблица 2.

---

Химический состав газа газоконденсатных месторождений, об. %

Месторождение	СН4	С2Н6	С3Н8	С4Н10	С5Н12	N2	СО2	Относит. плотность
Вуктыльское	74,80	7,70	3,90	1,80	6,40	4,30	0,10	0,882
Оренбургское	84,00	5,00	1,60	0,70	1,80	3,5	0,5	0,680
Ямбургское	89,67	4,39	1,64	0,74	2,36	0,26	0,94	0,713
Уренгойское	88,28	5,29	2,42	1,00	2,52	0,48	0,01	0,707

Газы, добываемые вместе с нефтью (попутный газ) представляют собой смесь метана, этана, пропан-бутановой фракции (сжиженного газа) и газового бензина. Содержание метана – около 35-85%. Содержание тяжёлых углеводородов в попутном газе 20-40% , реже – до 60% (табл. 3).

Таблица 3. Химический состав газа нефтяных месторождений (попутного газа), об. %

Месторождение	СН4	С2Н6	С3Н8	С4Н10	С5Н12	N2	СО2	Относит. плотность
Бавлинское	35,0	20,7	19,9	9,8	5,8	8,4	0,4	1,181
Ромашкинское	3838	19,1	17,8	8,0	6,8	8,0	1,5	1,125
Самотлорское	53,4	7,2	15,1	8,3	6,3	9,6	0,1	1,010
Узеньское	50,2	20,2	16,8	7,7	3,0	2,3	–	1,010

---

Тяжёлым нефтям свойственны сухие нефтяные газы (с преобладанием метана).

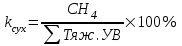(14)

Под тяжелыми УВ понимаются углеводороды от этана (С₂Н₆) и выше.

Лёгким нефтям свойственны жирные газы:

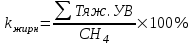(15)

Нефтяной газ при нормальных условиях содержит неполярные углеводороды (смесь компонентов от С₁ до С₄), и с точки зрения физики к ним можно применять законы для идеальных систем. С точки зрения математики – это аддитивная система. Следовательно, к нему при нормальных условиях применимы аддитивные методы расчётов физико-химических и технологических параметров (П_смеси):

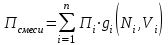, (16)

где g_i – весовая доля;

N_i – мольная доля;

V_i – объёмная доля;

П_i – параметр i-го компонента.

Плотность смеси газов рассчитывается следующим образом:

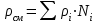. (17)

При нормальных условиях плотность газа _г = M_i / 22,414.

Нефтяной газ представлен в виде смеси углеводородов, поэтому для оценки его физико-химических свойств необходимо знать, как выражается состав смеси.

Массовая доля (g_i) – отношение массы i-го компонента, содержащегося в системе к общей массе системы:

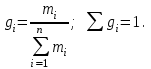(18)

Молярная (мольная) доля (N_i) – отношение числа молей i-го компонента к общему числу молей в системе:

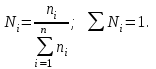(19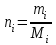

, (20)

где m_i – масса i-го компонента;

М_i – молекулярный вес.

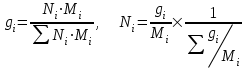(21)

Объёмная доля (V_i) – доля, которую занимает компонент в объёме системы.

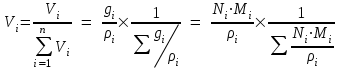(22)

Для идеального газа соблюдается соотношение V_i = N_i .

Молекулярная масса смеси рассчитывается следующим образом:

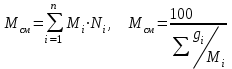(23)

Относительная плотность газа по воздуху:

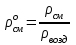. (24)

Для нормальных условий ρ_возд

---

 1,293; для стандартных условий ρ_возд  1,205.

Если плотность газа задана при атмосферном давлении (0,1013 МПа), то пересчёт её на другое давление (при той же температуре) для идеального газа производится по формуле:

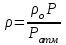. (25)

Смеси идеальных газов характеризуются аддитивностью парциальных давлений и парциальных объёмов.

Для идеальных газов давление смеси равно сумме парциальных давлений компонентов (закон Дальтона):

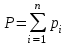, (26)

где Р – давление смеси газов;

р_i – парциальное давление i-го компонента в смеси,

или

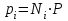. (27)

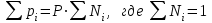. (28)

Т. е. парциальное давление газа в смеси равно произведению его молярной доли в смеси на общее давление смеси газов.

Аддитивность парциальных объёмов компонентов газовой смеси выражается законом Амага:

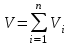(29)

где V – объём смеси газов;

V_i – объём i-го компонента в смеси.

или

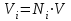. (30)

Для определения многих физических свойств природных газов используется уравнение состояния.

Уравнением состояния называется аналитическая зависимость между параметрами, описывающими изменение состояние вещества. В качестве таких параметров используется давление, температура, объём.

Состояние газа при стандартных условиях характеризуется уравнением состояния Менделеева-Клайперона:

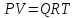, (31)

где Р – абсолютное давление, Па;

V – объём, м³;

Q – количество вещества, кмоль;

Т – абсолютная температура, К;

R – универсальная газовая постоянная Пам³/(кмольград).

У этого уравнения есть свои граничные условия. Оно справедливо для идеальных газов при нормальном (1 атм.) и близких к нормальному давлениях (10-12 атм.).

При повышенном давлении газ сжимается. За счёт направленности связи С-Н происходит перераспределение электронной плотности, и молекулы газов начинают притягиваться друг к другу.

Для учёта этого взаимодействия в уравнение (3.18) вводится коэффициент сверхсжимаемости

---

Смотрите также файлы

• Вопросы к государственному междисциплинарному экзамену по направлению подготовки 44. 03. 02 Психологопедагогическое образование, профиль Психология и педагогика начального образования.docx

• Дружба чудесное слово!.doc

• Суслова В. А. Существуют три группы неосознанных психических процессов.docx

• Укажите основные этапы эконометрического исследования.docx

• 1. Now, looking at your cv. I.docx