Файл: Слайд 2 фио Воренкова Екатерина Николаевна. Образование.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
( слайд 1) Защита
Здравствуйте
(слайд 2)
ФИО: Воренкова Екатерина Николаевна.
Образование: - высшее, 2012 год, квалификация «учитель математики», по специальности «математика»;
- 2014 г, освоила на отлично программу магистратуры по направлению подготовки «Педагогическое образование», присвоена квалификация «магистр».
Квалификационная категория: первая.
Стаж педагогической работы: 5 лет.
В данной должности: 5 лет.
В данном учреждении: 5 лет.
В настоящее время перед системой современного отечественного образования стоит важнейшей проблема: реализация компетентностного подхода в общеобразовательной школе.
Познавательная компетентность является ключевой компетентностью, формируемой в школе. Ее специфичность обусловлена во многом "привязанностью" к конкретной учебной дисциплине и возрастными особенностями школьников.
В структуре познавательной компетентности школьника, формируемой в процессе обучения математике, наряду с когнитивной, функциональной, социально-коммуникативной и мета-компетентностью, целесообразно рассматривать блок индивидуальных характеристик и личностных особенностей, а также систему взаимосвязей между компонентами [Пустовойтов В.Н. Познавательная компетентность старшеклассника: сущность категории и корреляты // European Social Science Journal (Европейский журнал социальных наук). Рига-Москва, 2012. №2(18). С.102-109.].
Современный подход к организации обучения и развития школьников предполагает целенаправленное управление не только усвоением знаний, формированием умений и навыков, но и мыслительной деятельностью учащихся, создание условий для их сознательности, активности и самостоятельности в учении. И, кроме того, такую организацию деятельности школьников, которая бы обеспечивала формирование у них умений и навыков самоанализа и самоконтроля в учении.
(Слайд 3)
Анализ нормативных документов Министерства образования и науки РФ, научной, методической и учебной литературы, а также результатов диссертационных исследований позволил выделить следующие противоречия:
(Слайд 4)
-
на социально-педагогическом уровне: между социально-обусловленными требованиями к уровню подготовки учащихся, выражающимися, в частности, в необходимости развития познавательной рефлексии и сложившейся системой школьного обучения, не позволяющей в достаточной мере выполнить современные требования к основному общему образованию; -
на научно-педагогическом уровне: между необходимостью развития познавательной рефлексии учащихся в процессе обучения и недостаточной разработанностью теоретических основ и дидактических средств ее развития; -
на научно-методическом уровне: между необходимостью развития познавательной рефлексии учащихся в процессе обучения математике и существующими методиками обучения, недостаточно направленными на развитие познавательной рефлексии.
(Слайд 5)
Из противоречий и ФГОС возникает проблема: как в процессе обучения математике обеспечить развитие познавательной рефлексии учащихся 5-6 классов.
Все выше сказанное может и должно рассматриваться как одна из форм педагогического формирования социального заказа школе, включающая в себя указания на существенный инвариант состава содержания образования, становление каждого человека рефлексирующей, саморазвивающейся и самореализующейся личностью.
Рефлексия позволяет учащимся понять себя, проанализировать свой собственный процесс мышления, являясь тем средством его самоорганизации и саморазвития и обеспечивая школьникам обратную связь в их учебной деятельности.
Рефлексия включает в себя предварительный анализ и осмысление предыдущих результатов, с четкими представлениями, зачем и почему это необходимо, и непременно, с возвратом назад с уже откорректированными представлениями, обновленными знаниями и критериями. Умение осуществлять такую деятельность предполагает сознательно организованный мыслительный процесс и овладение определенными средствами рефлексии.
(Слайд 6)
Объект исследования: процесс обучения математике учащихся 5-6 классов.
Предмет исследования: развитие познавательной рефлексии учащихся 5-6 классов в процессе обучения математике.
(Слайд 7)
Гипотеза: развитие познавательной рефлексии учащихся 5-6 классов в процессе обучения математике будет обеспечено, если в качестве средства развития познавательной рефлексии будут использованы рефлексивные задачи, которые направлены на формирование у учащихся умения проводить самостоятельный анализ решения задачи, умения рассматривать способы собственных действий (рефлексии). Также решение рефлективных задач должно быть направлено на формирование у учащихся учебных действий:
-
анализ условия задачи для обнаружения основного отношения; -
моделирование выделенного отношения в графической или знаковой форме; -
контроль за выполняемыми действиями; -
оценка освоения общего способа как результата решения данной задачи.
(Слайд 8)
Цель исследования: теоретическое обоснование и разработка методики развития познавательной рефлексии учащихся 5-6 классов в процессе обучения математике.
(Слайд 9)
В соответствии с целью и гипотезой исследования были поставлены следующие задачи:
1. На основе анализа психолого-педагогической, научно-методической литературы по проблеме исследования выделить рефлексивную задачу как одно из средств развития познавательной рефлексии в процессе обучения математике учащихся 5-6 классов.
2. Разработать структурно-функциональную модель развития познавательной рефлексии в процессе обучения математике учащихся 5-6 классов.
3. В соответствие с разработанной структурно-функциональной моделью научно обосновать и разработать методику развития познавательной рефлексии в процессе обучения математике учащихся 5-6 классов с помощью рефлексивных задач.
4. Осуществить экспериментальную проверку эффективности методики развития познавательной рефлексии в процессе обучения математике учащихся 5-6 классов.
(Слайд 10)
(таблица) В параграфе 1.1. результатом контент анализа стало следующее определение рефлексии: специфическая способность мыслительного процесса, направленную на осмысление и осознание собственных форм и предпосылок, размышление, самонаблюдение, самопознание, самоанализ, цепочка внутренних сомнений, обсуждений с собой, вызванным возникающими в жизни вопросами, трудностями, рядом событий, различными ситуациями, поиск вариантов ответа на происходящее или ожидаемое.
(Слайд 11)
Также в параграфе 1.1. получено определение познавательной рефлексии способность субъекта к осознанию процесса выполнения задания, которая предполагает, что при таком выполнении задания субъект учитывает свои возможности и способности, то есть осмысление и осознание собственных форм и предпосылок; особенности задания (инструкции); продуктивность способа достижения цели; умение оценивать, выделять, анализировать и соотносить с предметной ситуацией собственные действия.
(Слайд 12)
В последствии, было обосновано, что рефлексивные - это такие задачи, которые направлены на формирование у учащихся умения проводить самостоятельный анализ решения задачи, умения рассматривать способы собственных действий (рефлексии).
(Слайд 13)
Также решение рефлексивных задач должно быть направлено на формирование у учащихся следующих учебных действий:
-
анализ условия задачи для обнаружения основного отношения; -
моделирование выделенного отношения в графической или знаковой форме; -
контроль за выполняемыми действиями; -
оценка освоения общего способа как результата решения данной задачи»
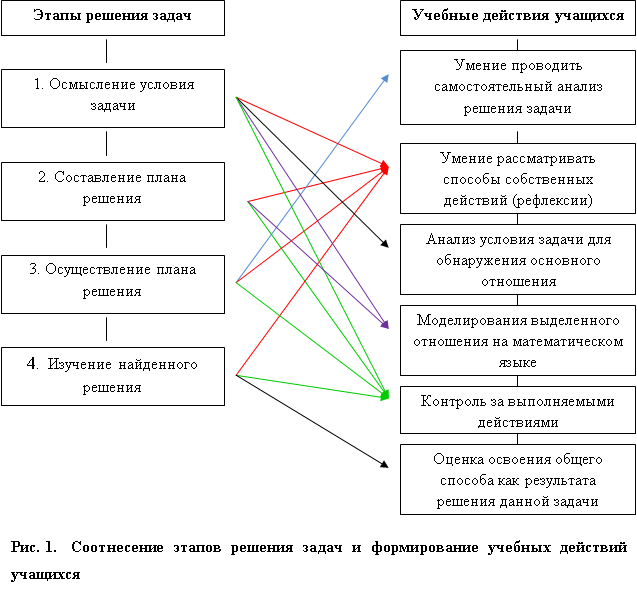
(Слайд 14)
(схема) В последствии анализа данных определений и определения рефлексивной задачи, было показано, что при решении рефлексивных задач формируются все необходимые умения учащихся для развития познавательной рефлексии.
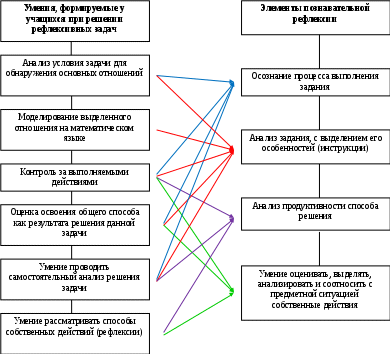
(Слайд 15)
Целью параграфа 1.3. являлось построение модели развития познавательной рефлексии в процессе обучения математики с использованием рефлексивных задач, ее вы можете рассмотреть более подробно на раздаточном материале.
Модель развития познавательной рефлексии учащихся 5-6 классов в процессе обучения математике

Методика развития познавательной рефлексии учащихся 6 класса
| Действия учителя | Действия учащегося | |||||||||
| 1 этап решения рефлексивных задач: осмысление условия задачи. | ||||||||||
| УД I. Анализ условия задачи для обнаружения основных отношений | ||||||||||
| 1. Назовите величины, которые связаны каким-либо отношением. 2. Назовите эти зависимости. | 1. Количество зерна в 1 и 2 элеваторе. 2. В первом в 2 раза больше, чем во втором. 3. Из 1 элеватора вывезли 600 т. 4. Во второй привезли 400 т. 5. После проделанных операций, количество зерна в элеваторах стало равным. | |||||||||
| УД II. Моделирование выделенного отношения на математическом языке | ||||||||||
| 1. Выполните запись условия задачи в виде таблицы. 2. Впишите все выделенные вами отношения. | Составляют таблицу (таб. 3) Таблица 3 Условие задачи
| |||||||||
| УД III. Контроль за выполняемыми действиями | ||||||||||
| 1. Проверьте, все ли зависимости вы выделили. 2. Верно ли вы их обозначили? 3. Закройте условие задачи и попробуйте по полученной таблице его воспроизвести. | 1. Выделяют отношения между величинами в условии задачи еще раз, проверяют все ли у них выписаны. 2. Проверяют правильность поставленных математических знаков («>», «=»). 3. Пытаются воспроизвести условие задачи, по составленной таблице. | |||||||||
| УД. VI. Умение рассматривать способы собственных действий (рефлексии) | ||||||||||
| 1. Понимаете ли вы, выделенные отношения между величинами, что они обозначают? 2. Нужно ли вам, выделять такие отношения для дальнейшей учебной деятельности и где это пригодится? | Например, возможны такие ответы: 1. В 1 элеваторе столько же зерна сколько в двух таких, какой 2. 2. Вывезли, т.е. стало меньше, а во втором стало больше. 3. Такое умение нужно при решении большинства задач, как в обучении, так и в жизни. | |||||||||
| 2 этап решения рефлексивных задач: составление плана решения. | ||||||||||
| УД II. Моделирование выделенного отношения на математическом языке | ||||||||||
| 1.Введите обозначение для неизвестной величины. 2. Произведите различные сочетания из данных и искомых величин, с помощью выделенных до этого отношений. 3. Составьте уравнение, как результат использования всех отношений. | 1. В таблице 3 заменяют неизвестное на х. 2. С помощью выделенных отношений, выражают все величины через х. 3. В результате получается новая таблица 4 Таблица 4 Составление плана решения
4. Составляют уравнение. | |||||||||
| УД III. Контроль за выполняемыми действиями | ||||||||||
| 1. Закройте условие задачи и таблицу 3, пользуясь таблицей 4, ответьте на вопрос: «Что означает левая (правая) часть полученного уравнения?». 2. Проверьте, все ли отношения вы правильно представили на математическом языке. | 1. Осталось в 1 элеваторе, стало во втором. 2. В 2 раза больше, значит нужно пользоваться операцией умножения. | |||||||||
| УД. VI. Умение рассматривать способы собственных действий (рефлексии) | ||||||||||
| 1. Возникли у вас затруднения, если да, то какие, как получилось справиться. 2. Что помогло вам в решении поставленной проблемы. | 1. Например, возникла ошибка при составлении левой части уравнения, вычитал из х (прибавил 600). 2. С данным затруднением справился после того, как использовал таблицу для воспроизведения условия задачи. | |||||||||
| 3 этап решения рефлексивных задач: осуществление плана решения. | ||||||||||
| УД. V. Умение проводить самостоятельный анализ решения задачи | ||||||||||
| 1. Вспомните необходимые правила для решения таких уравнений. 2. Не забудьте полностью ответить на вопрос задачи. | 1. Вспоминают правило (корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак) и применяют для решения. 2. Находят х – сколько тонн зерна было во 2 элеваторе и с помощью таблицы 4, находят 2х – сколько тонн зерна было в 1. | |||||||||
| УД III. Контроль за выполняемыми действиями | ||||||||||
| 1. Проверьте, нет ли ошибок в расстановке знаков. 2. На все ли вопросы ответили? | 1. Внимательно проверяют, правильно ли произвели перенос слагаемых из одной части в другую. 2. В задаче нужно было найти, сколько было зерна в каждом элеваторе, получили два ответа, значит, ответили на все вопросы. | |||||||||
| УД. VI. Умение рассматривать способы собственных действий (рефлексии) | ||||||||||
| 1. Возникли у вас затруднения при решении, если да, то какие, как получилось справиться. 2. Что помогло вам в решении поставленной проблемы. | 1. Не смог вспомнить правило или не смог его применить. 2. Посмотрел в учебнике, спросил у учителя. | |||||||||
| 4 этап. Изучение найденного решения. | ||||||||||
| УД. IV. Оценка освоения общего способа как результата решения данной задачи | ||||||||||
| 1. Запишите ответ. 2. Проверьте, верно ли вы решили задачу? Вспомните выделенные вами отношения. 3. Если решение не верное, решите еще раз, но, не используя неправильное решение. 4. С помощью чего вы решили данную задачу? 5. Когда мы можем использовать данный способ? | 1. Ответ: в 1 элеваторе было ___ т зерна, а во 2 __ т зерна. 2. В первом элеваторе должно получиться больше 600 т зерна, так как от туда вывозят, не может получиться отрицательного значения и т.п. 3. Решают еще раз, могут сделать проверку, по какому-либо отношению. 4. Данную задачу решали с помощью составления уравнения. 5. Такой способ можно использовать, когда недостаточно данных. | |||||||||
| УД III. Контроль за выполняемыми действиями | ||||||||||
| 1. Проверьте, правильно ли записали ответ. | 1. При записи ответа, следят, чтобы не перепутали найденные значения. 2. Проверяют правильность решения. 3. при неправильном решении еще раз повторяется 3 этап решения. | |||||||||
| УД. VI. Умение рассматривать способы собственных действий (рефлексии) | ||||||||||
| 1. Пригодится ли вам используемый способ решения? 2. Понятен ли был он вам? 3. Удобен ли вам такой способ? | 1. Отвечают, что пригодится в дальнейшем решении задач. 2. Если нет, то еще раз разбирают затруднения. 3. Если нет, то предлагают свой. | |||||||||
(Слайд 16)
Апробация результатов исследования:
-материалы исследования обсуждались на научно-методических семинарах МБОУ «СОШ № 1» г. Нижняя Тура,
(Слайд 17)
-основные положения исследования отражены в публикации «Рефлексивные задачи как средство развития познавательной рефлексии учащихся в процессе обучения математике», г. Саратов, 2014 г.
(Слайд 18)
Мониторинг за межаттестационный период представить не имею возможности в связи с отпуском по уходу за ребёнком. В этом учебном году имею стабильные положительные результаты освоения обучающимися образовательных программ по итогам мониторингов, проводимых организацией.
Общая успеваемость улучшилась с 87% до 95%.
Качественная успеваемость улучшилась с 37% до 41% по алгебре, с 33% до 41% по геометрии.
Систематически ведётся мониторинг обученности математике, позволяющий выстраивать индивидуальную траекторию коррекционной работы по устранению ошибок.
Развиваю у обучающихся способности к научной (интеллектуальной), творческой, физкультурно-спортивной деятельности. Реализую ФГОС в части проектной деятельности учащихся.
В 2017 – 2018 учебном году приняла участие в муниципальном фестивале «Современные образовательные технологии как средство повышения качества образования».
(Слайд 19)
На данном слайде представлены достижения моих учеников (подождать)
(Слайд 20)
В 2017 году мы принимали участие в муниципальном фестивале «Современные образовательные технологии как средство повышения качества образования».
(Слайд 21)
В 2018 году ученики 5 класса заняли 3 место в муниципальной игре «Час любителей математики».
(Слайд 22, 23)
(Слайд 24)
Личные достижения
- 2013 г., Благодарность Главы Заместителя декана по НИРС Математического факультета ФГБОУ ВПО «УрГПУ»;
за подготовку и проведение олимпиады по математике
- 2014 г., Благодарственное письмо Городского фестиваля противопожарной направленности «Звездный фейерверк!»;
- 2017 г., сертификат за участие в муниципальном фестивале «Современные образовательные технологии как средство повышения качества образования».
(Слайд 25)
Активно участвую в работе муниципального методического объединения учителей математики, школьного методического объединения ественно-научного цикла. Принимала участие в интегрированном турнире по математике