Задачи на разрезание помогают как можно раньше формировать геометрические представления у школьников на разнообразном материале. При решении таких задач возникает ощущение красоты, закона и порядка в природе.

На первом этапе рекомендуется рассмотреть задачи на клетчатой бумаге. Задачи, в которых разрезание фигур (в основном это квадраты и прямоугольники) идет по сторонам клеток.

Далее могут рассматриваться задачи, связанные с фигурами-пентамино. Пентамино́, изначально, (от др.-греч. πέντα пять, и домино) — пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами («ходом ладьи»). Сегодня пентамино понимается более широко – плоская фигура, составленная из плиток.

Задачи разбиения плоскости, в которых нужно находить сплошные разбиения прямоугольников на плитки прямоугольной формы, задачи на составление паркетов, задачи о наиболее плотной укладке фигур в прямоугольнике или квадрате, задачи, в которых одна фигура разрезается на части, из которых составляется другая фигура.

В наши дни любители головоломок увлекаются решением задач на разрезание, п

Примеры задач:

• 
  Разрежьте фигуру, изображенную на рисунке, на две равные части по линиям сетки так, чтобы в каждой из частей был кружок.
  

• 
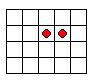
  На клетчатой бумаге нарисован квадрат размером 5*5 клеток. Придумайте, как разрезать его по линиям сетки на 7 различных прямоугольников.
  

Комбинаторика

В последние годы необычайно возросла роль комбинаторных методов не только в самой математике, но и в ее многочисленных приложениях: физике, химии, биологии, лингвистике, технике, экономике. Поэтому важно как можно раньше начать знакомить учащихся с комбинаторными методами и комбинаторными подходами. Изучение этой темы способствует развитию у учащихся «комбинаторного» мышления.

Главная цель, которую должен преследовать педагог при разборе и решении этих задач – осознанное понимание школьниками в какой ситуации при подсчете вариантов следует перемножать, а в какой – складывать. Для этого следует демонстрировать учащимся комбинаторные методы на большом количестве простых и конкретных примеров, продвигаясь вперед осторожно и постепенно. Не следует переходить к введению понятий «размещение» и «перестановки» пока это правило не освоено всеми учащимися.

---

Примеры и конструкции.

Примеры задач:

• 
  Среди четырёх людей нет трёх с одинаковым именем, или с одинаковым отчеством, или с одинаковой фамилией, но у каждых двух совпадает или имя, или отчество, или фамилия. Может ли такое быть?
  
• 
  Закрасьте некоторые клетки квадрата 4х4 так, чтобы любая закрашенная клетка имела общую сторону ровно с тремя незакрашенными.
  
• 
  Как расположить 16 шашек в 10 рядов по 4 шашки в каждом ряду? Как расположить 9 шашек в 10 рядов так, чтобы в каждом ряду было по 3 шашки? (ряд – это несколько шашек, лежащих на одной линии)
  

• 
  При делении числа 2•3=6 на 4 получаем в остатке 2. При делении числа 3•4=12 на 5 получаем в остатке 2. Верно ли, что остаток от деления произведения двух последовательных чисел на число, следующее за ними, всегда равен 2?
  

Повторение. Математическое соревнование.

По окончании цикла занятий проводится обобщающее занятие, в рамках которого проходит повторение изученного материала, а также проводится один из видов математического соревнования, который наиболее подходит для организации работы со школьниками, занятыми во внеурочной деятельности. Это может быть математический КВН, математический аукцион, математическая регата, игра по станциям, математический хоккей, математическое лото, мозговая атака и другие формы работы.
Итоговая олимпиада проводится как форма итогового занятия по освоению программы, определяющего объективный уровень знаний и умений учащихся, полученных в результате участия во внеурочной деятельности по математике. Мероприятие проводится по правилам проведения классической олимпиады по математике. Вариант работы составляется учителем. В работу включаются задания, которые были предметом обсуждения на занятиях внеурочной деятельности.

МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОГРАММЫ
Методической особенностью изложения учебных материалов на занятиях является такое изложение, при котором новое содержание изучается на задачах. Метод обучения через задачи базируется на следующих дидактических положениях:

• наилучший способ обучения учащихся, дающий им сознательные и прочные знания и обеспечивающий одновременное их умственное развитие, заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теоретические и практические задачи, решение которых даёт им новые знания;

---

• с помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями;

• усвоение учебного материала через последовательное решение задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой активности учащихся.

Большое внимание уделяется овладению учащимися математическими методами поиска решений, логическими рассуждениями, построению и изучению математических моделей.

Для поддержания у учащихся интереса к изучаемому материалу, их активность на протяжении всего занятия необходимо применять дидактически игры – современному и признанному методу обучения и воспитания, обладающему образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. Кроме того, на занятиях математического кружка необходимо создать "атмосферу" свободного обмена мнениями и активной дискуссии.

Исторический материал и работа с информацией входят в процесс обучения математике и в урочной деятельности, поэтому в рамках занятий внеурочной работы с учащимися рекомендуется при любой возможности мотивировать учащихся на занятия математикой очерками об истории математики, историями из жизни великих математиков, сведениями из достижений современной математической науки, т.е. самым широким образом популяризировать математику. Что касается работы с информацией, то любая встреча с математикой, точнее, с учебными задачами по математике непосредственно связана с «работой с информацией».

Содержание программы внеурочной деятельности связано с программой по предмету «математика» и спланировано с учетом прохождения программы 5 класса.

С другой стороны, следует учитывать, что реализация программы по внеурочной деятельности позволяет устранить противоречия между требованиями программы предмета «математика» и потребностями учащихся в дополнительном материале по математике и применении полученных знаний на практике; условиями работы в классно-урочной системе обучения математике и потребностями учащихся реализовать свой творческий потенциал. Одна из основных задач образования ФГОС второго поколения – развитие способностей ребенка и формирование универсальных учебных действий, таких как: целеполагание, планирование, прогнозирование, контроль, коррекция, оценка, саморегуляция. С этой целью в программе должно быть предусмотрено значительное увеличение активных форм работы, направленных на

---

вовлечение учащихся в динамическую деятельность, на обеспечение понимания ими математического материала и развития интеллекта, приобретение практических навыков самостоятельной деятельности.

Важно отметить, что количество часов, отводимых на реализацию программы невелико-34 часа в год, каждый учащийся должен «попробовать» и почувствовать вкус к тем или иным видам задач и сформировать относительно устойчивое умение решать эти задачи. Поэтому содержание программы устроено таким образом, что в рамках курса те или иные тематические разделы математики чередуются, естественно при этом темы не повторяются: элементы геометрии, логические задачи, текстовые задачи и т.д.

Замечательно, если постепенное освоение программы будет логично вписываться в общешкольные мероприятия, районные и городские мероприятия по математике: математические регаты, конкурсы, конференции и т.д.

С целью достижения качественных результатов желательно, чтобы занятия были оснащены современными техническими средствами, средствами изобразительной наглядности, игровыми реквизитами. С помощью мультимедийных элементов занятие визуализируется, вызывая положительные эмоции у обучающихся и создавая условия для успешной деятельности каждого ребёнка.
Эффективность и результативность программы внеурочной деятельности зависит от соблюдения следующих условий:

• 
  добровольность участия и желание проявить себя;
  
• 
  сочетание индивидуальной, групповой и коллективной деятельности;
  
• 
  сочетание инициатива детей с направляющей ролью учителя;
  
• 
  занимательность и новизна содержания, форм и методов работы;
  
• 
  эстетичность всех проводимых мероприятий;
  
• 
  чёткая организация и тщательная подготовка всех запланированных мероприятий;
  
• 
  наличие целевых установок и перспектив деятельности, возможность участвовать в конкурсах, олимпиадах и проектах различного уровня;
  
• 
  широкое использование методов педагогического стимулирования активности учащихся;
  
• 
  гласность, открытость, привлечение детей с разными способностями и уровнем овладения математикой.
  

ЛИТЕРАТУРА
Основная

1. 
   Анфимова Т.Б. Математика. Внеурочные занятия. 5-6 классы. – М.: Илекса, 2011.
   
2. 
   Вакульчик П.А. Сборник нестандартных задач. – Минск: БГУ, 2001.
   
3. 
   Генкин С.А., Итенберг И.В., Фомин Д.В. Математический кружок. Первый год. – Л.: С-Петербургский дворец творчества юных, 1992.
   
4. 
   Екимова М.А., Кукин Г.П. задачи на разрезание. – М.: МЦНМО, 2005.
   
5. 
   Игнатьев Е.И. В царстве смекалки. – М.: Наука, 1979.
   
6. 
   Канель-Белов А.Я., Ковальджи А.К. Как решают нестандартные задачи. – М.: МЦНМО, 2015.
   
7. 
   Математический кружок. Первый год обучения, 5-6 классы (Коллектив авторов). – М.: Изд. АПН СССР, 1991.
   
8. 
   Руденко В.Н., Бахурин Г.А., Захарова Г.А. Занятия математического кружка в 5 классе. – М.: Изд. дом «Искатель», 1999.
   
9. 
   Спивак А.В. Математический кружок. 6-7 классы. – М.: Посев, 2003.
   
10. 
    Спивак А.В. Математический праздник. – М.: МЦНМО, 1995.
    
11. 
    Столяр А. А. Зачем и что мы доказываем в математике. – Минск: Народная асвета, 1987.
    
12. 
    Шарыгин И.Ф., Шевкин А.В. Математика. Задачи на смекалку. 5-6 кл. – М.: Просвещение, 2001.
    
13. 
    Шейкина О.С., Соловьева Г.М. Математика. Занятия школьного кружка. 5-6 кл. – М.: НЦ ЭНАС, 2003.
    

---

Дополнительная

1. 
   Спивак А.В. Математический кружок. – М.: МЦНМО, 2015.
   
2. 
   Гарднер М. А ну-ка догадайся! – М.: Мир, 1984.
   
3. 
   Гарднер М. Есть идея! – М.: Мир, 1982.
   
4. 
   Гарднер М. Крестики-нолики. – М.: Мир, 1988.
   
5. 
   Гарднер М. Математические головоломки и развлечения. – М.: Мир, 1971.
   
6. 
   Гарднер М. Математические досуги. – М.: Мир, 1972.
   
7. 
   Гарднер М. Математические новеллы. – М.: Мир, 1974.
   
8. 
   Гарднер М. Путешествие по времени. – М.: Мир, 1990.
   
9. 
   Гик Е.Я. Замечательные математические игры. – М.: Знание, 1987.
   
10. 
    Гусев В.А., Орлов А.И., Розенталь А.Л. Внеклассная работа по математике в 6-8 классах. - М.: Просвещение, 1984.
    
11. 
    Кноп К. А. Взвешивания и алгоритмы: от головоломок к задачам. - М., МЦНМО, 2011.
    
12. 
    Кордемский Б.А. Математическая смекалка. – М., ГИФМЛ, 1958.
    
13. 
    Линдгрен Г. Занимательные задачи на разрезание. – М.: Мир, 1977.
    
14. 
    Пойа Д. Как решать задачу. – М.: Учпедгиз, 1961.
    
15. 
    Пойа Д. Математика и правдоподобные рассуждения. – М.: Наука, 1975.
    
16. 
    Пойа Д. Математическое открытие. – М.: Наука, 1970.
    
17. 
    Радемахер Г.Р., Теплиц О. Числа и фигуры. – М.: Физматгиз, 1962.
    
18. 
    Смаллиан Р. Алиса в стране Смекалки – М.: Мир, 1987.
    
19. 
    Смаллиан Р. Как же называется эта книга? – М.: Мир, 1981.
    
20. 
    Смаллиан Р. Принцесса или тигр? – М.: Мир, 1985.
    
21. 
    Смыкалова Е.В. Необычный урок математики. – СПб.: СМИО Пресс, 2007.
    
22. 
    Уфнаровский В.Л. Математический аквариум. – Кишинев: Штиинца, 1987.
    
23. 
    Фарков А.В. Математические олимпиады: методика подготовки 5-8 классы. – М.: ВАКО, 2012.
    
24. 
    Агаханов Н. X. Математика. Районные олимпиады. 6—11 классы / Агаханов Н.X., Подлипский О.К. — М.: Просвещение, 2010.
    

Примерные темы учебных проектов
6 класс

1. 
   Сумма углов треугольника на плоскости и на конусе.
   
2. 
   Совершенные числа.
   
3. 
   Четыре действия математики.
   
4. 
   Древние меры длины.
   
5. 
   Возникновение чисел.
   
6. 
   Счёты.
   
7. 
   Старинные русские меры или старинная математика.
   
8. 
   Магические квадраты.
   
9. 
   10.38 попугаев или как измерить свой рост.
   
10. 
    7 или 13? Какое число счастливее?
    
11. 
    Великие женщины-математики.
    
12. 
    Великие задачи.
    
13. 
    Великолепная семерка.
    
14. 
    Величайший математик Евклид.
    
15. 
    Веселые задачки.
    
16. 
    Веселый урок для пятиклассников.
    
17. 
    Весёлые задачки для юных рыбаков.
    
18. 
    Витамины и математика.
    
19. 
    Единицы измерения длины в разных странах и в разное время.
    
20. 
    Жизнь нуля - цифры и числа.
    
21. 
    Задачи-сказки.
    
22. 
    Задачник "Эти забавные животные".
    
23. 
    Закодированные рисунки.
    
24. 
    Замечательная комбинаторика.
    
25. 
    Математика в играх.
    
26. 
    Мое любимое занятие – шашки.
    
27. 
    Число в русском народном творчестве.
    
28. 
    Число и числовая мистика.
    
29. 
    Число, которое больше Вселенной.
    
30. 
    Числовые великаны.
    
31. 
    Числовые забавы.
    
32. 
    Числовые суеверия.
    

---

Смотрите также файлы

• Практическая работа по мдк 02. 02 Методика проведения инвентаризации активов и финансовых обязательств организации.docx

• 1. Многоэтажное общественное здание 1 Исходные данные.docx

• Слайд 2 фио Воренкова Екатерина Николаевна. Образование.docx

• Тема Политические права и свободы человека и гражданина в России Темы докладов (презентаций).docx

• Практическая 3 Задание.docx