Файл: Отчёт по лабораторной работе 5 Момент инерции различных тел. Теорема Штейнера.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.12.2023

Просмотров: 667

Скачиваний: 52

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

ОТЧЁТ

ПО ЛАБОРАТОРНОЙ РАБОТЕ №5
Момент инерции различных тел. Теорема Штейнера

По дисциплине Физика

(наименование учебной дисциплины, согласно учебному плану)

Выполнил: студент гр. ОНГ-22 Дзюба М.М.

(шифр группы) (подпись) (Ф.И.О.)

Дата:
Проверил:



(должность) (подпись) (Ф.И.О.)

Санкт-Петербург

2022

  1. Цель работы

Измерить моменты инерции различных тел. Проверить теорему Штейнера.

  1. Краткое теоретическое содержание

Явления, изучаемые в работе: инертность и вращательное движение.

Инертность – свойство тела изменять свою угловую скорость под действием одной и той же силы.

Вращательное движение – это движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей.

Момент инерции – мера инертности тела при вращательном движении.

Момент инерции сплошного твёрдого тела определяется по формуле



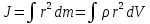
Где r – расстояние от элемента объема V с массой m до оси вращения, 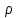– плотность вещества

Формула, используемая для вывода расчетной формулы:


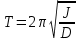(Период крутильных колебаний); [T] = с

J - момент инерции,

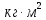
D – модуль кручения пружины,

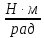
Теорема Штейнера - момент инерции относительно произвольной оси O1O1 равен сумме момента инерции J0, относительно оси OO, параллельной данной и проходящей через центр масс тела и произведения массы тела на квадрат расстояния d между осями.





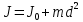
  1. 3
    С хема установки

7 -

1




8

2



9



5

4



10

6

Рис. 1. Общий вид экспериментальной установки

1 – Световой барьер, 2 – Спиральная пружина, 3 – сплошной цилиндр, 4 – стержень, 5 – динамометр, 6 – линейка, 7 – полый цилиндр, 8 – шар, 9 – диск, 10 – грузы на стержне

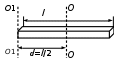
Рис.2 Схема установки для проверки Теоремы Штейнера

  1. Основные расчетные формулы

Момент инерции: 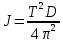[J] =

T – период крутильных колебаний, с; D – модуль кручения пружины,

Момент инерции шара:

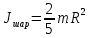
m – масса шара, кг; R – радиус шара, м

Момент инерции стержня:

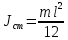
m – масса стержня, кг; l – длина стержня, м

Момент инерции сплошного цилиндра:

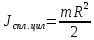
m – масса цилиндра, кг; R – радиус цилиндра, м

  1. Формулы погрешности косвенных измерений





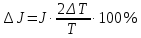
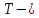измеренное значение периода колебаний, с

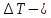абсолютная погрешность периода колебаний, с

  1. Таблицы + числовые значения для проверки теоремы Штейнера

Таблица 1

Физическая величина
φ
F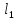


M

Единица измерения

№ опыта
рад
Н
м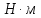


1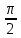


0,5
0,048
0,0240

2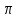


1
0,048
0,0480

3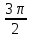


1,5
0,048
0,0816

4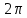


2
0,048
2,5480

Таблица 2

Физическая величина
r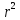


T
J

Единица измерения

№ опыта
м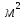


с


1
0,048
0,002304
2,9664
0,00637

2
0,068
0,004624
3,1970
0,00740

3
0,088
0,007744
3,5070
0,00891

4
0,108
0,011664
3,8690
0,01084

Таблица 3

Физическая величина
r
m
T1
T2
T3
T4
T5

Единица измерения

Исследуемое тело
м
кг
с
c
c
c
c

шар
0,0690
0,765
1,716
1,716
1,716
1,716
1,716

сплошной цилиндр
0,0495
0,343
1,019
1,018
1,018
1,019
1,019

Данные для проверки теоремы Штейнера

m = 0,131кг – масса стержня

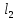= 0,6м – длина стержня

T0 = 2,819 c – период колебаний несмещенного стержня

d = 0,02 м - смещение стержня относительно оси вращения

  1. Вычисления

Постоянные параметры

– плечо силы, м;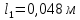

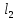
– длина стержня, м;









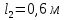
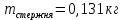
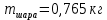
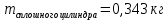
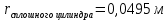
Погрешности прямых измерений + случайная погрешность периода





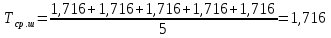
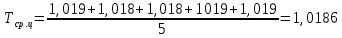
Среднее квадратичное отклонение:



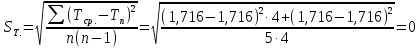
Инструментальная погрешность:





=



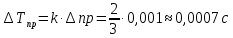
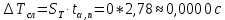
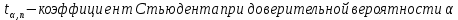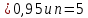
Абсолютная погрешность измерения периода:





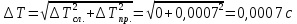
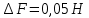
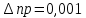м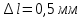





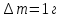
Основные вычисления











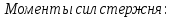
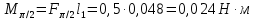
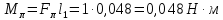
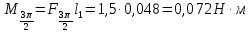
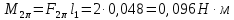
Момент инерции шара:





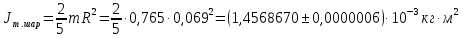
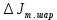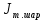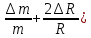= ( *100%= 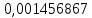*( *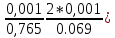100%=0,00004%

Смотрите также файлы